DOI: 10.11817/j.issn.1672-7207.2017.09.017
一种求解面向服务软件部署优化问题的多目标蚁群算法
李琳1, 2,应时1, 2,董波1, 2
(1. 武汉大学 软件工程国家重点实验室,湖北 武汉,430072;
2. 武汉大学 计算机学院,湖北 武汉,430072)
摘要:基于根据动态变化的外部环境调整面向服务软件的部署方案是提升其运行性能、降低运行成本的一种有效途径,提出一种基于多目标蚁群算法的MACO-DO,以便在自动为面向服务软件寻找一组在性能和成本之间作出最优权衡的部署方案。MACO-DO算法是对传统多目标蚁群算法的一种改进,引入摒弃精英解策略以避免算法早熟收敛,设计1个局部搜索过程以加快获得可行解的过程。在Case 1,Case 2和Case 3共3种不同规模的模拟案例上将提出的MACO-DO算法与P-ACO算法和NSGA-Ⅱ算法进行对比。研究结果表明:MACO-DO算法在求解问题上具有更好的性能。
关键词:面向服务软件;部署优化;多目标蚁群算法;性能
中图分类号:TP311 文献标志码:A 文章编号:1672-7207(2017)09-2376-12
A multi-objective ant colony algorithm for deployment optimization of service-oriented application
LI Lin1, 2, YING Shi1, 2, DONG Bo1, 2
(1. State Key Lab of Software Engineering, Wuhan University, Wuhan 430072, China;
2. School of Computer Science, Wuhan University, Wuhan 430072, China)
Abstract: Considering that optimizing the deployment architecture of service-oriented software according to the changes in runtime environment is an efficient way to improve its performance and reduce its cost, a multi-objective ant colony algorithm MACO-DO was proposed for the automatic exploration of search space to find a set of pareto optimal deployment architectures for a service-oriented application quickly. MACO-DO is an improved version of the traditional multi-objective ant colony algorithm. A strategy of discarding elitist solutions was introduced to prevent the algorithm from prematuring convergence and a local search procedure was designed to accelerate the process of obtaining feasible solutions. A series of experiments were implemented on three simulated cases (i.e. Case 1, Case 2 and Case 3) of different sizes to verify the efficiency of MACO-DO and it was compared with P-ACO and NSGA-Ⅱ. The results show that MACO-DO has better performance than others on the considered problem.
Key words: service-oriented software; deployment optimization; multi-objective ant colony algorithm; performance
面向服务软件通常运行在一个开放的、动态的环境中[1]。环境的变化可能会导致在长时间运行过程中出现性能降级或成本浪费的情况,为此,软件开发商和性能工程师通常需要根据环境的变化动态优化软件的部署方案。然而,为面向服务的软件制定最优的部署方案并不容易,需要面对以下挑战:首先,面向服务软件可能的部署方案非常多,通过搜索整个部署空间寻找最优方案将耗费大量的时间和成本;其次,性能提升与成本降低往往相互冲突,寻找最优部署方案需要在它们之间进行权衡。因此,寻找最优部署方案最重要的是在冲突的优化目标之间进行最优权衡,而不只是寻找单个目标最优的部署方案。目前,软件部署优化领域成果较多。JAYASINGHE等[2]提出了一种基于结构化约束敏感的软件部署方法,以实现大规模的软件部署与优化过程。MALEK等[3]提出了一种可扩展的部署优化框架,能够根据用户QoS偏好找到最合适的软件部署方案。WHITE等[4]提出一种混合型空间部署优化算法ScatterD,以实现无线网络上实时系统的最优拓扑结构的自动生成。张晓薇等[5]提出了一种体系结构驱动的网络化移动应用部署方案优化方法,以生成满足用户个性化需求的部署方案。然而,上述研究都是将部署优化问题转化为单目标优化问题,为获得最优方案,需要精确定义各目标之间的权重,而这通常很难实现[6]。南国芳等[7]提出了一种多目标遗传算法,从网络覆盖和能量消耗2个方面求解移动感知节点的部署优化问题。WADA等[8]提出了一种多目标遗传算法E3-R解决面向服务等级协议(service level agreements,SLAs)的服务部署优化问题。FREYS等[9]设计了一种新颖的遗传算法CDOXPLORE处理云环境下的软件部署优化问题。YUSOH等[10-12]基于遗传算法提出了一列优化方法,解决了组合SAAS软件的放置、构件聚类和可扩展性问题。然而,上述研究均采用遗传算法求解多目标的软件部署优化问题,算法收敛速度慢。目前,利用蚁群算法求解部署优化问题方面的研究还较少。ALETI等[13]利用基于蚁群的P-ACO算法自动搜索嵌入式软件系统的部署优化策略。该算法将软件部署优化问题形式化为1个多目标、多约束的优化问题,并将其与多目标遗传算法(MOGA)进行对比。实验显示,在算法运行初期,P-ACO算法比MOGA算法能够更快地找到较优解,然而,随着优化过程的持续进行,P-ACO容易陷入局部最优解。为解决上述问题,本文作者提出一种基于多目标蚁群算法的面向服务软件部署优化方法。该方法的核心是1个基于多目标蚁群算法的部署优化算法(multi-objective ant colony optimization for deployment optimization,MACO-DO)。该算法充分利用蚁群算法快速收敛的特性,同时有效克服了其容易陷入局部最优解的不足,能快速地为面向服务软件寻找满足性能与成本需求,并在它们之间作出权衡,使得软件供应商能够更好地理解优化目标之间的权衡,从而根据他们的需求和偏好作出更明智的决策。
1 问题描述
1.1 模型描述
本文的目的是通过优化面向服务软件的部署方案来处理由于环境变化而导致的性能降级和成本浪费问题。该优化问题主要涉及4个方面:面向服务的软件、部署平台、运行环境和需求约束。为了求解这些问题,需要首先给出与这4个方面相关的一些参数。
假设1个面向服务软件由一组服务组成,记为 。函数
。函数 指定每个服务对1个请求的基准处理时间,即当分配给每个服务具有单位计算能力的资源时,它们处理1个请求所需的时间。服务对请求的实际处理时间与分配给它们的资源的计算能力呈正比。函数
指定每个服务对1个请求的基准处理时间,即当分配给每个服务具有单位计算能力的资源时,它们处理1个请求所需的时间。服务对请求的实际处理时间与分配给它们的资源的计算能力呈正比。函数 用于指定每个服务运行所需的内存空间。函数
用于指定每个服务运行所需的内存空间。函数 用于定义任意服务之间的交互关系。
用于定义任意服务之间的交互关系。 表示服务sj在服务si执行完成以后才执行;
表示服务sj在服务si执行完成以后才执行;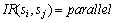 表示服务si和服务sj并行执行;
表示服务si和服务sj并行执行;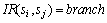 表示服务si与服务sj按一定的概率选择执行;
表示服务si与服务sj按一定的概率选择执行;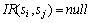 表示服务si与服务sj之间没有直接交互关系。
表示服务si与服务sj之间没有直接交互关系。
假设1个部署平台由一组硬件主机组成,记为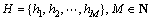 ,函数
,函数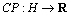 指定每个硬件主机的计算能力,函数
指定每个硬件主机的计算能力,函数 指定每个硬件主机可用的内存空间,函数
指定每个硬件主机可用的内存空间,函数 指定每个硬件节点的运行成本。对于运行环境,只考虑每个服务的平均请求到达率,它是平均单位时间内到达每个服务的请求数,用函数
指定每个硬件节点的运行成本。对于运行环境,只考虑每个服务的平均请求到达率,它是平均单位时间内到达每个服务的请求数,用函数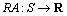 表示。
表示。
本文的目标是提升软件的运行性能、降低软件的运行成本。性能通常为多个指标的综合体现[14],其中,响应时间、吞吐量和利用率是用于评估软件性能最常见的3个指标。响应时间通常定义为1个软件对1个请求端到端的响应时间,即用户从请求软件服务到接收其返回结果所耗费的时间,它与用户对软件性能的直观感受相一致。吞吐量定义为软件单位时间内可以处理的请求数,它反映了软件的处理能力。利用率指1个硬件主机在运行过程中被占用的时间比率,能够用于评估1个硬件主机是否被合理利用。本文也采用这3种常见的性能指标来评估面向服务软件的性能,只是利用率定义为所使用的硬件主机利用率的最大值。因为面向服务的软件通常运行在一个开放、动态的环境中,在软件运行过程中,具有最大利用率的硬件主机很容易成为瓶颈,因此,该值在一定程度上反映了部署方案对变化环境的适应能力。考虑成本主要是为了避免不必要的资源浪费。这里的成本主要考虑部署面向服务软件所使用主机的运行成本总和。
面向服务软件端到端的响应时间和吞吐量需要根据它所包含的服务之间的交互关系,聚合各服务的响应时间和吞吐量来获得。假设在部署方案d下, ,
,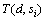 和
和 分别为服务si的响应时间、吞吐量和硬件主机hj的利用率,
分别为服务si的响应时间、吞吐量和硬件主机hj的利用率,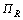 和
和 分别为响应时间和吞吐量的聚合函数;
分别为响应时间和吞吐量的聚合函数; 和
和 分别为面向服务软件端到端的响应时间和吞吐量;
分别为面向服务软件端到端的响应时间和吞吐量;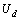 为运行软件的所有硬件主机的利用率的最大值;
为运行软件的所有硬件主机的利用率的最大值; 为所有硬件主机的总运行成本。本文的优化目标可以表示为:
为所有硬件主机的总运行成本。本文的优化目标可以表示为:


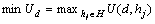
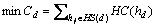 (1)
(1)
1个可行的部署方案需要满足一些特定的约束。就部署本身而言,需要满足的约束为内存约束,即部署在1个硬件主机上的所有服务对内存需求的总和不能超过该硬件主机的可用内存。此外,对于优化目标而言,软件供应商通常会有一个可接受的范围,因此,也需要对它们进行约束。由于本文的优化目标是尽可能降低响应时间、最大利用率和运行成本,而将吞吐量最大化,因此,对于响应时间、最大利用率和运行成本都有1个可接受的最大值Rmax,Umax和Cmax,而对于吞吐量则有1个可接受的最小值Tmin。对于其他约束,本文主要考虑位置约束和同位约束2种,并分别用函数 和
和 表示。位置约束主要约束服务到特定硬件主机的分配关系。
表示。位置约束主要约束服务到特定硬件主机的分配关系。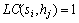 表示服务si可以部署在硬件主机hj上,而
表示服务si可以部署在硬件主机hj上,而 则表示服务si不能部署在硬件主机hj上;同位约束主要指约束服务之间的位置关系。
则表示服务si不能部署在硬件主机hj上;同位约束主要指约束服务之间的位置关系。 表示服务si和sj必须部署在同一个硬件主机上;
表示服务si和sj必须部署在同一个硬件主机上;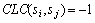 表示服务si和sj不能部署在同一个硬件主机上,
表示服务si和sj不能部署在同一个硬件主机上, 表示服务si和sj之间不存在位置约束。设函数DH(d, si)用于获取部署服务si的硬件主机。基于上述描述,1个可行的部署方案d需要满足的约束条件可以表示为:
表示服务si和sj之间不存在位置约束。设函数DH(d, si)用于获取部署服务si的硬件主机。基于上述描述,1个可行的部署方案d需要满足的约束条件可以表示为:

1.2 性能估算方法
排队论是估算分布式软件性能的一种有效方法,已经得到大量应用[15-16]。本文利用排队论估算各服务的响应时间和各硬件主机的利用率,并将1个硬件主机建模为1个M/M/1/PS队列。由于所有的指标都需要基于1个特定的部署方案来进行估算,因此,需要给出一些与部署有关的参数。给定1个部署方案d,设函数 用于获取部署在硬件主机hj上的所有服务,si为部署在 hj上的1个服务,即
用于获取部署在硬件主机hj上的所有服务,si为部署在 hj上的1个服务,即 ,则硬件主机hj在部署方案d下的利用率为
,则硬件主机hj在部署方案d下的利用率为
 (3)
(3)
式中: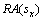 和
和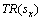 分别表示服务sx的请求到达率和基准响应时间;
分别表示服务sx的请求到达率和基准响应时间; 表示硬件主机hj的计算能力;
表示硬件主机hj的计算能力; 表示硬件主机hj上的服务sx对1个请求的实际处理时间。从式(3)可以看出:当
表示硬件主机hj上的服务sx对1个请求的实际处理时间。从式(3)可以看出:当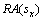 足够大时,硬件主机hj的利用率
足够大时,硬件主机hj的利用率 将超过100%,这不符合实际情况。因此,需要将
将超过100%,这不符合实际情况。因此,需要将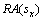 降低到
降低到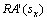 ,使得
,使得 为100%。由上述分析可知:当
为100%。由上述分析可知:当 小于100%时,服务sx的吞吐量
小于100%时,服务sx的吞吐量 等于它的请求到达率
等于它的请求到达率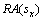 ,否则,
,否则, 等于
等于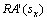 ,即
,即
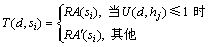 (4)
(4)
假设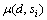 为服务si在部署方案d下的平均服务率,即si在单位时间内可处理的请求数,可表示为
为服务si在部署方案d下的平均服务率,即si在单位时间内可处理的请求数,可表示为
 (5)
(5)
则根据排队论知识可得服务si的响应时间为
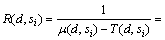
 (6)
(6)
下面以1个实例来说明如何计算1个服务的响应时间、吞吐量以及1个硬件主机的利用率。假设在部署方案d下,服务s1和s2部署在硬件主机h1上;s1和s2的基准响应时间 和
和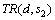 分别为0.05 s和 0.02 s,h1的计算能力
分别为0.05 s和 0.02 s,h1的计算能力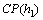 为2,它们在2种不同的场景下运行。在第1种场景下,服务s1和s2的平均请求到达率
为2,它们在2种不同的场景下运行。在第1种场景下,服务s1和s2的平均请求到达率 和
和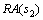 分别为8 次/s和15 次/s,则根据式(3)可得h1的利用率
分别为8 次/s和15 次/s,则根据式(3)可得h1的利用率 为35%,没有超过 100%。因此,服务s1和s2的吞吐量
为35%,没有超过 100%。因此,服务s1和s2的吞吐量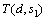 和
和 分别为8 次/s和15 次/s;s1的响应时间
分别为8 次/s和15 次/s;s1的响应时间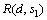 约为0.038 s,s2的响应时间
约为0.038 s,s2的响应时间 约为 0.015 s。 在第2种场景下,
约为 0.015 s。 在第2种场景下, 和
和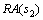 分别为32 次/s和60 次/s,则根据式(3)可得
分别为32 次/s和60 次/s,则根据式(3)可得 为140%,超过100%。因此,
为140%,超过100%。因此, 和
和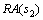 需要降低为
需要降低为 和
和 ,以确保
,以确保 等于100%。本文采用的方法是根据
等于100%。本文采用的方法是根据 和
和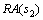 的比值降低它们的值,即
的比值降低它们的值,即 ,
,
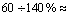
 。这时,
。这时, 降低为100%;
降低为100%;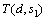 和
和 分别为26.7 次/s和50 次/s;
分别为26.7 次/s和50 次/s;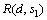 和
和 为无限大。
为无限大。
根据上述分析可知:当1个硬件主机的利用率达到100%时,部署在它上面服务的平均响应时间将为无穷大,这对于服务供应商和用户来说都无法接受。因此,1个可行的部署方案必须确保每个硬件主机的利用率不能达到或超过100%。在这种情况下,服务的吞吐量将等于它的请求到达量。也就是说,在特定负载情况下,软件在可行部署方案下的吞吐量将保持不变,优化部署方案,将不会对吞吐量产生影响。因此,本文将所需满足的吞吐量定义为服务的请求到达率,将响应时间、最大利用率和运行成本作为优化目标,以获取面向服务软件的最优部署方案。
在得到每个服务的响应时间和吞吐量后,可以根据服务之间的交互关系,利用表1中的聚合函数计算软件端到端的响应时间和吞吐量。
表1 聚合函数
Table 1 Aggregate functions

2 基于蚁群优化的MACO-DO算法
蚁群算法产生于20世纪90年代,是Dorigo等[17]从蚂蚁觅食行为中获得设计灵感而提出的,用于求解复杂组合优化问题的一种元启发式智能优化技术[18]。该算法的基本思想是:种群中的每只蚂蚁通过逐步选择解组件来构建问题的解,并在构建解的路径上留下一定量的信息素,每次迭代结束后,记录当前构建的历史最优解;蚂蚁之间通过信息素进行经验交流,信息素的更新用于指导后续蚂蚁的搜索行为,当达到终止条件时,算法结束。
在面向服务软件部署优化问题中,蚂蚁构建的每个解对应1种可能的部署方案,解组件对应软件服务到虚拟机的1种分配,蚂蚁通过一步步选择相应的解组件来构建部署方案。当所有服务都被分配到1个相应的虚拟机时,1个部署方案就构建完成。
为了采用蚁群算法解决多目标的面向服务软件部署优化问题,本文在MACO-DO算法中,针对每个优化目标分别设计相应的信息素和启发式,以指导蚂蚁朝着最优解的方向搜索;设计摒弃精英解策略用于抑制算法的早熟收敛;设计局部搜索策略,以加快获得最优解;最后给出算法的总体描述。
2.1 信息素与启发式的设计
信息素和启发式用于指导蚂蚁的选择。本文分别使用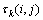 和
和 表示解组件i, hj>(表示服务si部署在硬件主机hj上)与目标第k个目标相关的信息素和启发式。
表示解组件i, hj>(表示服务si部署在硬件主机hj上)与目标第k个目标相关的信息素和启发式。
在算法开始执行时,需要为每个信息素设置1个初始值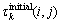 。由于本文问题模型中定义的位置约束LC能够帮助算法在构建部署方案之前排除一些不可行的方案组件,因此,本文结合位置约束定义部署方案构建过程中使用的信息素初始值,将不满足位置约束LC的方案组件信息素值设置为0,以此阻止蚂蚁选择这些不可行的方案组件,即
。由于本文问题模型中定义的位置约束LC能够帮助算法在构建部署方案之前排除一些不可行的方案组件,因此,本文结合位置约束定义部署方案构建过程中使用的信息素初始值,将不满足位置约束LC的方案组件信息素值设置为0,以此阻止蚂蚁选择这些不可行的方案组件,即
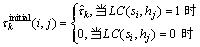 (7)
(7)
式中: 根据第k个目标进行定义。本文的优化目标仅包含响应时间、利用率和成本,这些优化目标都有1个上限值(即可接受的最大值),因此,
根据第k个目标进行定义。本文的优化目标仅包含响应时间、利用率和成本,这些优化目标都有1个上限值(即可接受的最大值),因此, 可定义为第k个目标的上限值的倒数:
可定义为第k个目标的上限值的倒数:
 (8)
(8)
启发式 的定义也基于第k个目标。由于本文的目标均为最小化目标,因此,启发式的设计应指导蚂蚁倾向于选择对目标值贡献最小的组件,即
的定义也基于第k个目标。由于本文的目标均为最小化目标,因此,启发式的设计应指导蚂蚁倾向于选择对目标值贡献最小的组件,即

 (9)
(9)
式中: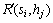 ,
,  和
和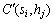 分别表示将服务si分配到硬件主机hj时,已部署服务(包括si)的聚合响应时间、所有硬件主机利用率的最大值和当前的运行成本。
分别表示将服务si分配到硬件主机hj时,已部署服务(包括si)的聚合响应时间、所有硬件主机利用率的最大值和当前的运行成本。
2.2 方案的构建
在MACO-DO中,蚂蚁根据信息素和启发式的值选择解组件以构建部署方案。在选择解组件过程中,约束函数LC和CLC将被用于阻止蚂蚁构建不可行的部署方案。蚂蚁对解组件的选择遵循伪随机比例规则,即选择解组件时,需要首先产生[0, 1]之间的1个随机数q,并将其与用户定义的参数q0进行比较。若q<q0,则将被选择的解组件 为
为
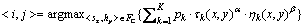 (10)
(10)
否则,采用轮盘选择规则完成服务到虚拟机的分配。在轮盘选择规则中,选择解组件 的概率
的概率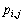 为
为
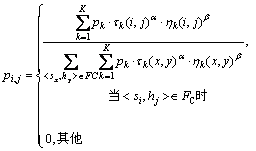 (11)
(11)
式中:FC表示可行的解组件集;pk为第k个目标的权重,它由蚂蚁在优化过程中随机生成,具体生成过程见文献[19];α和β为参数,它们决定了选择过程中启发式信息和信息素的相对重要性,若α>β,则蚂蚁的选择受信息素值的影响更大;若α<β,则蚂蚁的选择受启发式值的影响更大。
面向服务软件部署方案的伪代码如下:

2.3 信息素的管理
在MACO-DO算法中,信息素的管理主要包括信息素的局部更新和信息素的全局更新2部分。信息素的局部更新在蚂蚁选择1个解组件之后执行,旨在提高蚂蚁构建的解的多样性;信息素的全局更新在每一轮循环结束时(即所有蚂蚁完成1次部署方案构建时)执行,旨在指导蚂蚁朝着最优解的方向构建解。
信息素的局部更新主要通过降低蚂蚁已选择的解组件所对应的信息素值,使得后续蚂蚁有更大的机会选择其他解组件,以构建不同的解,提高解的多样性。假设蚂蚁选择方案组件 ,则该组件与第k个目标相关的信息素利用下式进行局部更新:
,则该组件与第k个目标相关的信息素利用下式进行局部更新:
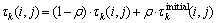 (12)
(12)
其中:ρ为信息素的挥发率,位于区间(0, 1]之间。
信息素的全局更新主要通过增加与精英解(即当前最优部署方案)所对应的信息素的值,引导蚂蚁在精英解周围进行搜索。通常,精英解为当前搜索得到的拥有1个或多个目标最优值的解。假设方案组件 属于精英解ek,则利用式(13)对该组件与第k个目标相关的信息素执行全局更新:
属于精英解ek,则利用式(13)对该组件与第k个目标相关的信息素执行全局更新:
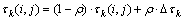 (13)
(13)
其中: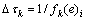 ,为精英解ek的第k个目标值的倒数。基于这些定义,随着算法演化,精英解的目标函数值越来越小,
,为精英解ek的第k个目标值的倒数。基于这些定义,随着算法演化,精英解的目标函数值越来越小,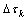 也越来越大。换句话说,更多的信息素将被添加到当前精英解的组成成分上,使得它们对后续迭代过程中的蚂蚁更具吸引力。
也越来越大。换句话说,更多的信息素将被添加到当前精英解的组成成分上,使得它们对后续迭代过程中的蚂蚁更具吸引力。
2.4 摒弃精英解策略
虽然使用上述精英策略(即增加精英解解组件上的信息素的值)有助于蚂蚁集中探索当前最优方案附近的搜索区域,但它也会导致算法过早收敛于局部最优解。因为当精英解在多次迭代过程中保持不变时,根据式(13),信息素将大量聚集在精英解的组件上,导致蚂蚁在后续搜索过程中仅在这些解组件中进行选择。
为了解决这一问题,本文参考文献[20],设计1种摒弃精英解的优化策略,即为精英解(也称为全局精英解)设置1个允许其在搜索过程中保持不变的最大迭代数 。当1个精英解保持不变的迭代次数超过该值时,将使用本次迭代过程中产生的解集中对应的精英解(也称为局部精英解,它仅在当前迭代过程中产生的解集中为精英)替代当前精英解。假设
。当1个精英解保持不变的迭代次数超过该值时,将使用本次迭代过程中产生的解集中对应的精英解(也称为局部精英解,它仅在当前迭代过程中产生的解集中为精英)替代当前精英解。假设 ,为全局精英解集;ei为第i个目标值最优的全局精英解;
,为全局精英解集;ei为第i个目标值最优的全局精英解; ,为迭代次数集,其中每个值代表1个全局精英解保持不变的迭代次数,即
,为迭代次数集,其中每个值代表1个全局精英解保持不变的迭代次数,即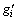 为精英解ei保持不变的迭代次数;
为精英解ei保持不变的迭代次数; 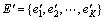 为当前迭代过程中产生的局部精英解;
为当前迭代过程中产生的局部精英解;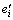 为第i个目标值最优的局部精英解;对集合E中的每个精英解ei,若
为第i个目标值最优的局部精英解;对集合E中的每个精英解ei,若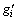 ≥
≥ ,则用
,则用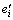 替换ei以更新集合E。
替换ei以更新集合E。
2.5 局部搜索策略
现有的研究工作显示,当将ACO算法与局部搜索算法相结合时,算法能够得到更好的结果[21]。因此,为了进一步改进所提出的MACO-DO算法的性能,本文为MACO-DO算法设计1个局部搜索策略。它应用于蚂蚁每次迭代之后和执行全局信息素更新规则之前,基于现有的领域知识,根据优化目标在精英解的领域进行搜索,以加快搜索最优解的过程。
本文的优化目标是降低面向服务软件端到端的响应时间、硬件节点利用率的最大值以及软件的运行成本。其中,资源供应是影响响应时间和利用率的主要因素,而使用的硬件主机数和各硬件主机的运行成本是影响运行成本的主要因素。根据这一分析,本文定义5种局部搜索规则。
1) 将1个服务从利用率较高的(源)硬件主机移动到利用率较低的(目的)硬件主机上,且保证移动后,目的主机的利用率不超过源主机移动之前的利用率。假设Uj和Uk分别为硬件主机hj和hk当前的利用率,si为部署在hj上的1个服务,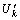 为将si移动到hk上后hk的利用率。若Uj>Uk且
为将si移动到hk上后hk的利用率。若Uj>Uk且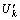 ≤
≤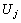 ,则将si从hj上移动到hk上。这里,hk可以是已使用的硬件主机,也可以是还未被使用的硬件主机。
,则将si从hj上移动到hk上。这里,hk可以是已使用的硬件主机,也可以是还未被使用的硬件主机。
2) 将利用率较高的硬件主机上占用资源较少的服务与利用率较低的硬件节点上占用资源较多的服务交换位置,且保证交换后这2个硬件主机利用率的最大值不大于交换前的最大值。假设Uj和Uk分别为硬件主机hj和hk的当前利用率,si和st分别为hj和hk上的1个服务, 和
和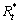 分别为si和st对计算资源的需求,
分别为si和st对计算资源的需求,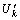 为si和st交换位置后hk的利用率。若Uj>Uk,
为si和st交换位置后hk的利用率。若Uj>Uk, >
>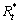 且
且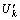 ≤
≤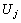 ,则交换si和st的位置,即将si移动到hk上,将st移动到hj上。
,则交换si和st的位置,即将si移动到hk上,将st移动到hj上。
3) 使用1个拥有更多计算资源的新硬件主机替换当前硬件主机。假设hj 为当前使用的1个硬件主机,hk为1个未被使用的硬件主机,Pj和Pk分别为hj和hk的计算能力,若Pj<Pk,则将部署在hj上的所有服务移动到hk上。
4) 使用1个拥有较低运行成本的新硬件主机替换当前硬件主机。假设hj为当前使用的1个硬件主机,hk为1个未被使用的硬件主机,Cj和Ck分别为hj和hk的运行成本,若Cj>Ck,则将部署在hj上的所有服务移动到hk上。
5) 将利用率最低的硬件主机上的服务移动到其他已使用的硬件主机上,以不再使用该主机。假设hj为当前已使用的硬件主机中利用率最低的主机,若其他已使用的主机拥有足够的资源部署该主机上的服务(即移动后个主机的利用率不会大于预定义的最大值Umax,且1个主机上的所有服务对内存资源的需求总和不大于该硬件主机可用的内存空间),则将该主机上的服务移动到其他硬件主机上。
在上述5种规则中,规则①~③能够提高服务的响应时间和利用率,因此,将它们应用于响应时间最短或最大利用率最低的精英解上,以期望搜索目标值更优的新精英解,且在将它们应用于利用率最低的精英解上时,具有较高利用率的硬件主机(即hj)为利用率最大的硬件主机,规则④和⑤则能够有效地将软件的运行成本。因此,将它们应用于成本最低的精英解上。虽然应用这些优化策略并不能保证产生的新部署方案一定优于当前的Pareto最优解,但相比随机搜索过程,它们为寻找最优部署方案提供了一定的引导作用,因此,能够获得比随机搜索更高的搜索效率。
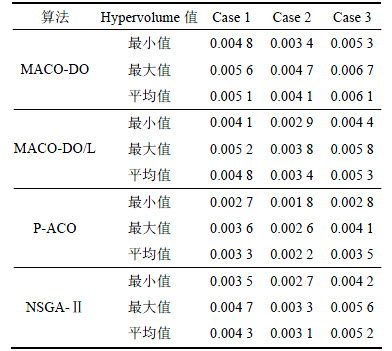
假设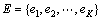 为当前的全局精英解集,
为当前的全局精英解集,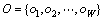 为当前的Pareto最优解集,其中
为当前的Pareto最优解集,其中 为当前获得的Pareto最优解的数量。给出如算法2所示的局部搜索过程的伪代码。
为当前获得的Pareto最优解的数量。给出如算法2所示的局部搜索过程的伪代码。

2.6 算法总体描述
算法3给出了MACO-DO算法的处理过程。A和gmax分别表示种群中蚂蚁的个数和算法迭代的最大次数。在算法刚开始时,根据2.1节中的定义初始化信息素和启发式。在每一次迭代过程中,种群中的每只蚂蚁将构建1个新解并对其进行评估,若该解为1个新的精英解或Pareto最优解,则利用该解对集合O和E进行更新。然后,基于该解进行信息素局部更新。在每次迭代结束后,检查每个精英解保持不变时的迭代次数。若存在1个精英解保持不变时的迭代次数超过预定义的最大值 ,则将摒弃该精英解,并按照2.4节中的描述向集合E中添加1个新精英解。然后,执行信息素的全局更新。
,则将摒弃该精英解,并按照2.4节中的描述向集合E中添加1个新精英解。然后,执行信息素的全局更新。

3 实验设计与结果分析
3.1 实验数据与环境
为了验证MACO-DO算法的有效性,在3个不同规模的模拟实例上,将MACO-DO与P-ACO算法[15]和NSGA-Ⅱ算法[22]进行对比。实验中所有的案例都采用模拟的方式生成。其中,用于对比MACO-DO与其他近似算法的3个模拟案例(记为Case 1,Case 2和Case 3)中,各面向服务软件所包含的服务数分别为12,25和50,部署这些服务所能接受的最大成本分别为400,900和2 000 $,所有硬件节点可接受的利用率上限值为0.8。
本实验的其他部分参数由在指定范围类随机生成的数据进行填充,其范围如下:TR∈[1,20], SR∈[2,8], RA∈[200,400], CP∈[1,5], AS∈[10,30], HC∈[30,80]。服务之间的交互关系根据概率随机指定。本文共考虑顺序、选择、并发和不交互这4种交互关系,选择每种交互关系的概率均为0.25。随机选择的交互关系必须确保每个服务都包含在同一个流程中,还有一些参数则需要根据这些参数的值进行确定。如组合服务的最大响应时间必须根据组合服务中各服务的响应时间以及服务之间的交互关系确定,否则可能会导致有效的部署方案不存在,或导致该约束无效。
蚁群算法和遗传算法都属于近似方法。由于近似方法的参数配置会极大地影响算法的性能[23],为了给算法寻找最合适的参数配置,通常需要对不同配置的参数组合进行测试。本文参考文献[10,11,15],根据文献中的参数设置,给出算法中每个参数的变化范围和变化步长,并通过反复试验,得出本文实验中算法的最优参数配置。在执行参数确定的实验之前,有些参数可以根据文献直接确定,如可设蚁群算法(即MACO-DO,MACO-DO/L和P-ACO)的种群数AN=10,信息素参数α=1,遗传算法的种群数P=100。其他参数则根据测试结果得出,各参数的变化范围和变化步长如表2所示。根据实验测试结果,本文得出各算法的具体参数配置如下:对于MACO-DO和MACO- DO/L和P-ACO算法,信息素更新率ρ=0.1,参数β=2,伪随机比例参数q0=0.5;对于NSGA-Ⅱ算法,杂交率pc=0.9,变异率pm=0.1。
表2 算法参数的变化范围和步长
Table 2 Changing scopes and step lengths of parameters

由于近似算法采用的是随机搜索过程,执行结果难以预测,通常需要对这些算法进行多次、独立地重复执行,并取重复执行得到的结果的平均值表征它们的性能。本实验中,各算法针对每个实例独立运行30次,并取30次独立执行的平均结果进行对比实验。
实验的硬件平台环境为:CPU Inter Core(TM)2 Duo 3.16 GHz,内存DDR3 4 GB,硬盘500 GB;软件平台为操作系统64bit Windows 7,算法实现工具MyEclipse8.5,编程语言为Java。
3.2 目标值分析
本节主要根据目标函数值(即平均响应时间、最大利用率和成本),对比所提出的算法与其他算法的性能。表3所示为各算法在3个不同规模的模拟案例上独立运行30次所得解集的所有目标函数最优值的平均值和标准方差(STD)。其中,目标函数的标准方差(STD)反映了解集分布的集中程度。为了客观比较,各算法在同一案例上运行的终止条件相同,即在案例1上运行30 000次评估、在案例2上运行40 000次评估,在案例三上运行50 000次评估。为了进行更全面对比,将基于MACO-DO算法但不采用局部搜索的算法记为MACO-DO/L,并给出其运行结果,以便与其他算法进行对比。
表3 根据目标函数值对比算法MACO-DO,MACO-DO/L,P-ACO和NSGA-Ⅱ的性能
Table 3 Performance comparisons among algorithms MACO-DO,MACO-DO/L,P-ACO and NSGA-Ⅱ with objective values
从表3可以看出:在3种规模的实验案例中,MACO-DO算法都能够为各目标函数找到更优值,且即使不采用局部搜索,提出的MACO-DO算法仍然能够找到较好解;此外,MACO-DO算法的解集具有较小的标准方差,这说明该算法得到的解集更稳定。
这些算法的演化曲线见图1~3。演化曲线上的值为30次独立运行过程中,每隔1 000次评估所记录的对应目标函数最优值的平均值。
从图1~3可以看出:与NSGA-Ⅱ算法相比,MACO算法(包括MACO-DO,MACO-DO/L和P-ACO)通常能够在搜索刚开始时就找到较好解,这是因为这些算法采用了非常有用的启发式指导解的构建过程。但NSGA-Ⅱ算法最终能够比P-ACO算法获得更好的解,这说明P-ACO算法比NSGA-Ⅱ算法更容易陷入局部最优;P-ACO算法比MACO-DO/L算法能够更快地找到较好的解,且收敛速度快,但MACO-DO/L算法最终能够比P-ACO算法找到更好的解,这是因为MACO-DO/L算法采用了摒弃精英方案的策略,虽然稍微减缓了算法的收敛速度,但保证了算法能够找到更好的解,且相对于解的质量而言,减缓的收敛速度是可以接受的;MACO-DO算法比MACO-DO/L算法能够更快地找到更好的解,且能够在优化过程中始终保持这一优势,这说明MACO-DO算法采用的局部搜索过程能够有效地提高算法的收敛速度,同时也能在一定程度上进一步提高算法的求解质量。

图1 各算法在Case 1上运行所得到的各目标值的演化曲线
Fig. 1 Evolutionary curves of objectives for all algorithms on Case 1

图2 各算法在Case 2上运行所得到的各目标值的演化曲线
Fig. 2 Evolutionary curves of objectives for all algorithms on Case 2
3.3 处理时间分析
表4所示为每个算法处理上述3种不同规模案例(即在案例1上运行30 000次评估、在案例2上运行40 000次评估和在案例3上运行50 000次评估)的时间,结果是30次独立运行的平均时间和标准方差。
从表4可以看出:各算法的处理时间相差不大,因此,当以相同的评估次数作为算法的终止条件时,最终能够获得较好目标函数值的算法。根据目标函数值的对比结果可知 MACO-DO算法能够最终获得具有较好目标函数值的部署方案,因此,与其他算法相比具有更好的性能。另外,从图1~3可看出:MACO-DO算法比其他算法具有更快的收敛速度,因此,若以否收敛作为算法的终止条件,则MACO-DO算法仍然具有较少的时间。

图3 各算法在Case 3上运行所得到的各目标值的演化曲线
Fig. 3 Evolutionary curves of objectives for all algorithms on Case 3
表4 各算法运行时间对比
Table 4 Processing time of each algorithm s

从表4还可看出:MACO-DO算法的处理时间较少,这是因为使用的局部搜索策略只是对现有的部署方案进行局部调整,因此,在计算调整后的部署方案性能时,只需对受调整影响的部分服务的性能进行重新计算,其他服务的性能则保持不变,这在一定程度上降低了部署方案的性能估算时间。
3.4 Hypervolume分析
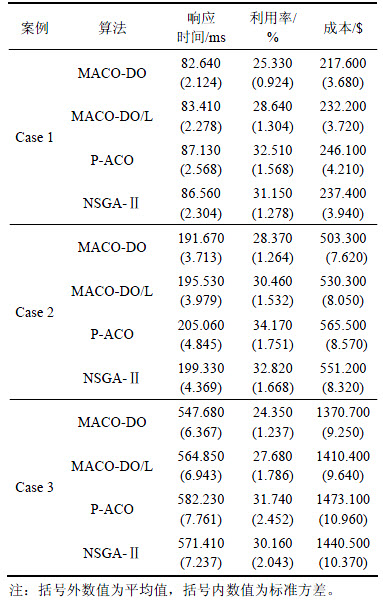
每个算法在每个Case上独立运行30次所得解集的hypervolume的最大值、最小值和平均值见表5。从表5可以看出:MACO-DO/L算法求得解集的最大、最小和平均hypervolume值均比P-ACO算法和NSGA-Ⅱ算法的大,这说明MACO-DO/L算法比P-ACO算法和NSGA-Ⅱ算法的求解质量高。这是因为MACO-DO/L算法中采用的摒弃精英策略使得算法
表5 各算法Hypervolume值对比
Table 5 Hypervolume comparson of solution sets from each algorithm
能够朝着更多的方向进行优化,有效地降低了算法过早收敛于局部最优解的可能性。从表5还可见: MACO-DO算法所得解集的hypervolume值的各统计量比MACO-DO/L算法的相应值更优,这说明MACO-DO算法比MACO-DO/L算法更有效,其主要原因是MACO-DO算法采用的局部搜索策略根据现有部署方案的性能评估值对其进行优化调整,使得算法能够更快地找到问题的可行解,同时,也在一定程度上提高了算法找到最优解的可能性。
4 结论
1) 提出了一种新的多目标蚁群算法MACO-DO来解决面向服务软件部署优化问题。该算法充分利用蚁群算法能够使用基于问题的启发式指导蚂蚁快速找到问题的最优解这一特性,为每个优化目标设计了相应信息素和启发式;同时还设计一种新的摒弃精英解策略,以避免算法早熟收敛。此外,它还引入一些有用的领域知识进行局部搜索,以进一步改进算法的性能。
2) 所设计的摒弃精英解策略和局部搜索过程都能够有效地提高算法的搜索效率,与现有的算法相比,MACO-DO算法能够获得具有更低最大利用率、更低响应时间和更低成本的部署方案。
参考文献:
[1] TRUMMER I, FALTINGS B, BINDER W. Multi-objective quality-driven service selection: a fully polynomial time approximation scheme[J]. IEEE Transactions on Software Engineering, 2014, 40(2): 167-191.
[2] JAYASINGHE D, PU C, EILAM T, et al. Improving performance and availability of services hosted on iaas clouds with structural constraint-aware virtual machine placement[C]// Proceedings of 2011 IEEE International Conference on Services Computing(SCC). Washington DC, USA: IEEE, 2011: 72-79.
[3] MALEK S, MEDVIDOVIC N, MIKIC-RAKIC M. An extensible framework for improving a distributed software system's deployment architecture[J]. IEEE Transactions on Software Engineering, 2012, 38(1): 73-100.
[4] WHITE J, DOUGHERTY B, THOMPSON C, et al. ScatterD: spatial deployment optimization with hybrid heuristic/ evolutionary algorithms[J]. ACM Transactions on Autonomous and Adaptive Systems, 2011, 6(3): 123-154.
[5] 张晓薇, 曹东刚, 陈向群, 等. 一种网络化移动应用部署方案优化方法[J]. 软件学报, 2011, 22(12): 2866-2878.
ZHANG Xiaowei, CAO Donggang, CHEN Xiangqun, et al. Deployment solution optimization for mobile network application[J]. Journal of Software, 2011, 22(12): 2866-2878.
[6] 林闯, 陈莹, 黄霁崴, 等. 服务计算中服务质量的多目标优化模型与求解研究[J]. 计算机学报, 2015, 38(10): 1907-1923.
LIN Chuang, CHEN Ying, HUANG Jiwe, et al. A survey on models and solutions of multi-objective optimization for QoS in services computing[J]. Chinese Journal of Computers, 2015, 38(10): 1907-1923.
[7] 南国芳, 陈忠楠. 基于进化优化的移动感知节点部署算法[J]. 电子学报, 2012, 40(5): 1017-1022.
NAN Guofang, CHEN Zhongnan. Deployment algorithm of mobile sensing nodes based on evolutionary optimization[J]. Chinese Journal of Electronics, 2012, 40(5): 1017-1022.
[8] WADA H, SUZUKI J, YAMANO Y, et al. Evolutionary deployment optimization for service-oriented clouds[J]. Software Practice and Experience, 2011, 41(5): 469-493.
[9] FREYS, FITTKAU F, HASSELBRING W. Search-based genetic optimization for deployment and reconfiguration of software in the cloud[C]// Proceedings of the 2013 International Conference on Software Engineering. San Francisco, USA: IEEE, 2013: 512-521.
[10] YUSOH Z I M, TANG M. A cooperative coevolutionary algorithm for the composite SaaS placement problem in the cloud[C]// Neural Information Processing: Theory and Algorithms. Heidelberg: Springer, 2010: 618-625.
[11] YUSOH Z I M, TANG M. A penalty-based grouping genetic algorithm for multiple composite saas components clustering in cloud[C]// Proceedings of the 2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC). Seoul, Korea: IEEE, 2012: 1396-1401.
[12] YUSOH Z I M, TANG M. Composite SaaS placement and resource optimization in cloud computing using evolutionary algorithms[C]// Proceedings of the 2012 IEEE 5th International Conference on Cloud Computing (CLOUD). Chicago, USA: IEEE, 2012:590-597.
[13] ALETI A, GRUNSKE L, MEEDENIYA I, et al. Let the ants deploy your software: an ACO based deployment optimization strategy[C]// Proceedings of the 24th IEEE/ACM International Conference on Automated Software Engineering. Auckland, New Zealand: IEEE, 2009: 505-509.
[14] CORTELLESSA V, DI MARCO A, INVERARDI P. Model- based software performance analysis[M]. Springer Science & Business Media, 2011: 1-30.
[15] KHAZAEI H, 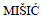 J,
J,  V B. Performance analysis of cloud computing centers using m/g/m/m+ r queuing systems[J]. IEEE Transactions on Parallel and Distributed Systems, 2012, 23(5): 936-943.
V B. Performance analysis of cloud computing centers using m/g/m/m+ r queuing systems[J]. IEEE Transactions on Parallel and Distributed Systems, 2012, 23(5): 936-943.
[16] VILAPLANA J, SOLSONA F,  I, et al. A queuing theory model for cloud computing[J]. The Journal of Supercomputing, 2014, 69(1): 492-507.
I, et al. A queuing theory model for cloud computing[J]. The Journal of Supercomputing, 2014, 69(1): 492-507.
[17] Dorigo M, Gambardella L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 53-66.
[18] DORIGO M, ST TZLE T. Ant colony optimization: overview and recent advances[M]. Springer, US: Handbook of Metaheuristics, 2010: 227-263.
TZLE T. Ant colony optimization: overview and recent advances[M]. Springer, US: Handbook of Metaheuristics, 2010: 227-263.
[19] IREDI S, MERKLE D, MIDDENDOEF M. Bi-criterion optimization with multi colony ant algorithms[C]// Evolutionary Multi-Criterion Optimization. Heidelberg, Germany: Springer, 2001: 359-372.
[20] MERKLE D,MIDDENDORF M,SCHMECK H.Ant colony optimization for resource-constrained project scheduling[J]. IEEE Transactions on Evolutionary Computation,2002,6(4): 333-346.
[21] LENSTRA J K. Local search in combinatorial optimization[M]. Princeton University Press, 2003: 436-451.
[22] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
[23]  M, PELLEGRINI P, et al. Parameter adaptation in ant colony optimization: autonomous search[M]. Heidelberg, Germany: Springer 2012:191-215.
M, PELLEGRINI P, et al. Parameter adaptation in ant colony optimization: autonomous search[M]. Heidelberg, Germany: Springer 2012:191-215.
(编辑 陈灿华)
收稿日期:2016-10-16;修回日期:2016-12-24
基金项目(Foundation item):国家高技术研究发展计划(863计划)项目(2012AA011204);国家自然科学基金资助项目(61373038) (Project (2012AA011204) supported by the National High Technology Research and Development Program (863 Program) of China; Project(61373038) supported by the National Natural Science Foundation of China)
通信作者:应时,博士,教授,从事高性能软件的开发、语义Web技术、软件体系结构和模式等研究;E-mail: ngshi0601@163.com