J. Cent. South Univ. (2017) 24: 17-29
DOI: 10.1007/s11771-017-3404-1
Soft measurement model of ring’s dimensions for vertical hot ring rolling process using neural networks optimized by genetic algorithm
WANG Xiao-kai(汪小凯)1, 2, HUA Lin(华林)1, 3, WANG Xiao-xuan(汪晓旋)4,
MEI Xue-song(梅雪松)2, ZHU Qian-hao(朱乾浩)5, DAI Yu-tong(戴玉同)5
1. Hubei Key Laboratory of Advanced Technology for Automotive Components,
Wuhan University of Technology, Wuhan 430070, China;
2. College of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;
3. Hubei Collaborative Innovation Center for Automotive Components Technology, Wuhan 430070, China;
4. National Automobile Quality Supervision Test Center, Xiangyang 441004, China;
5. Zhangjiagang Hailu Annular Forgings Co., Ltd., Zhangjiagang 215626, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: Vertical hot ring rolling (VHRR) process has the characteristics of nonlinearity, time-variation and being susceptible to disturbance. Furthermore, the ring’s growth is quite fast within a short time, and the rolled ring’s position is asymmetrical. All of these cause that the ring’s dimensions cannot be measured directly. Through analyzing the relationships among the dimensions of ring blanks, the positions of rolls and the ring’s inner and outer diameter, the soft measurement model of ring’s dimensions is established based on the radial basis function neural network (RBFNN). A mass of data samples are obtained from VHRR finite element (FE) simulations to train and test the soft measurement NN model, and the model’s structure parameters are deduced and optimized by genetic algorithm (GA). Finally, the soft measurement system of ring’s dimensions is established and validated by the VHRR experiments. The ring’s dimensions were measured artificially and calculated by the soft measurement NN model. The results show that the calculation values of GA-RBFNN model are close to the artificial measurement data. In addition, the calculation accuracy of GA-RBFNN model is higher than that of RBFNN model. The research results suggest that the soft measurement NN model has high precision and flexibility. The research can provide practical methods and theoretical guidance for the accurate measurement of VHRR process.
Key words: vertical hot ring rolling; dimension precision; soft measurement model; artificial neural network; genetic algorithm
1 Introduction
The medium-size rings whose diameter is less than 1000 mm, such as rail way bearing rings, spindle bearing rings and pipe flange rings, are the fundamental parts in modern industry. Vertical hot ring rolling (VHRR) process is the most effective forming technology for manufacturing these ring products [1, 2]. Its working principle is shown in Fig. 1. The driving roll rotates around its axis and advances gradually toward the mandrel roll at a given feed rate; the mandrel roll is freely mounted, which rotates under the friction. Under the pressure between driving roll and mandrel roll, the ring’s diameter increases and the cross-section is formed [3, 4]. The drive roll rotates around its own axis and moves toward the mandrel roll. The mandrel roll passively rotates around its fixed axis under the friction. The guide roll, which is used to maintain the ring rolling process stability, is also fixed in an appropriate place. The ring passes the gap between the drive roll and the mandrel roll, and the metal incremental plastic deformation occurs under the extrusion of the rolls, which cause the ring to shape the profile and expand the diameter, when the ring’s dimensions reach the required values, the feeding stops and the VHRR process finishes [1]. Up to now, a lot of research of radial-axial ring rolling process for large scale rings has been carried out [5], such as the theoretical analysis [6, 7], macroscopic deformation rules [8] and equipment research [9]. These studies have promoted the rolling technology for the large scale rings. However, literature on VHRR process and its measurement and control method is relatively scarce. WANG and HUA [10] established the simple VHRR measurement model based on the analytical and experimental method. However, the model is not suitable for the situation that the ring blank’s dimensions and the guide roll’s position are changed. In addition, the model cannot measure the ring’s inner diameter. On the basis of the studies mentioned above, this work aims at the practical issues of the actual VHRR production, analyze the relationships between the parameters of the ring blanks, the guide roll’s position, the displacement of the measuring roll and the ring’s dimensions, combined the finite element (FE) simulations and experiments of VHRR, establishes the soft measurement neural network (NN) model of the ring’s dimensions based on the radial basis function neural network (RBFNN). Finally, the verification experiments is conducted to tests the soft measurement NN model, the results show that the soft measurement model has high measurement precision and flexibility, the research conclusions can supply a new approach to the on-line measurement for VHRR process.
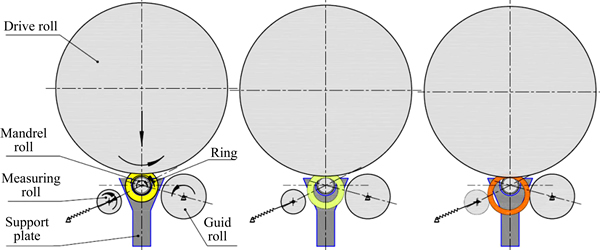
Fig. 1 Working principle of VHRR process [3]
2 Soft measurement model of ring’s dimensions for VHRR based on RBFNN
Unlike the radial-axial large ring rolling process, there are no axial rolls on VHRR mill, and the ring’s axial deformation is restrained by the closed rolling pass [11]. The guide mode of VHRR process generally adopts single fixed guide roll, which results in the formed ring deviating from the symmetrical centerline of the drive roll and mandrel roll at the final rolling stage, as shown in Fig. 1. In addition, the rolling time of VHRR process is short (The rolling time of the ring product whose outer diameter is enlarged from 250 to 350 mm takes 4-6 s), the ring’s growth rate is fast and the position of the guide roll needs frequent adjustment. These factors leads the ring’s dimensions cannot be measured directly. Radial basis function neural network (RBFNN) has the advantages of simple structure, fast convergence rate and universal approximation [12]. It is suitable for modeling the nonlinear system. In this work, the RBFNN is utilized to establish the measurement model of the ring’s dimensions for VHRR.
2.1 Data sample acquisition of soft measurement NN model
The data sample obtained from VHRR experiment is limited. However, a mass of process data samples can be obtained from VHRR finite element (FE) simulation. So the VHRR FE models with different guide roll’s positions and different ring blanks are established and simulated in ABAQUS software.
2.1.1 3D coupled thermo-mechanical FE model of VHRR
The 3D coupled thermo-mechanical FE model for VHRR, as shown in Fig. 2, is established according to the method proposed by WANG et al [13]. The contact pairs are defined between the ring and rollers. The friction and contact heat conduction exist at the interface of each contact pair. The rectangular section ring is considered as the subject investigated. The material of ring blank is bearing steel GCr15 and its true stress- strain behaviors with respect to different temperature curves are the same as those in Ref. [14]. The geometrical and movement parameters of VHRR FE models are summarized in Table 1. Reduced integration and hourglass control are employed to improve calculative efficiency and avoid the zero-energy mode, respectively. The adaptive mesh technology is adopted to control the distortion of the elements of the ring.
2.1.2 Data acquisition method of VHRR FE model
Least square circle method [13] is a common method to evaluate the rolled ring’s roundness. In FE model, a set of evenly spaced nodes are selected at the ring’s circumference, and several sensors are established in ABAQUS to obtain the coordinates of the nodes during the simulation. The ABAQUS/Explicit subroutine VUAMP of least square circle method is utilized and called at each time step. Then, the ring’s outer diameter,center coordinate and roundness error can be calculated during FE simulation. According to actual characteristics of VHRR mill, the axial connector element and beam connector element are employed to simulate the spring and piston rod of the measuring roll in ABAQUS to obtain the measuring roll’s displacement, as shown in Fig. 2.

Fig. 2 3D coupled thermo-mechanical FE model for VHRR
Table 1 Geometrical and movement parameters of VHRR FE models

2.1.3 Selection of ring blanks’ dimensions and positions of guide roll
Generally speaking, the dimensions of the mandrel roll are almost invariant to the same type of VHRR mill. And the ring blank’s inner diameter refers the standard that the center hole of the ring blanks can pass through the mandrel roll smoothly, so all of the ring blanks’ inner diameters in FE model are set as 120 mm in this work. To ensure that the data sample obtained from the FE simulations can cover the VHRR process for ring blanks with different sizes, five different sizes of ring blanks are selected, four of them whose D0=220, 240, 260 and 280 mm are set as the training samples of the NN model, and another one whose D0=250 mm is set as the test sample. Besides, in order that the modeling method can be applied to other specifications of ring products, the setting method of the guide roll’s position is described as follows: Assuming that the formed ring keeps symmetric and the angle of the central line between ring blank and the guide roller to X axis remain constant during rolling process, the moving path of guide roll will be approximately straight line. Therefore, a series of angles and the ratios of the guide roll’s position on the line of ring and guide roller’s center are selected as the variable parameters of guide roll’s position, as shown in Fig. 3.The guide roll’s position of different blank sizes are illustrated in Table 2.

Fig. 3 Position setting schematic diagram of guide roll
During the VHRR process, a proper position of guide roll is very important. When the distance between the guide roll and the ring blank is too close, the formed ring will be squashed, on the contrary, the unstable rolling time will be increased, and then the ring’s roundness will be influenced, as shown in Fig. 4, resulting in inaccurate measurement data. So, the simulation results of these two conditions should not be used for establishing the soft measurement NN model. The ratios of the guide roll’s position of the FE models listed in Table 2 are selected according to the fact that the roundness error of the formed ring is less than 1.5 mm during FE simulation.
2.1.4 Analysis of FE simulation results and data processing
Figure 5 shows the relationship curves between ring’s outer diameter and the displacement of the measuring roll of all FE model groups. It can be seen that the ring’s outer diameter is almost linear with the measuring roll’s displacement for the same blank sizes and invariant guide roll’s position. However, when ring blank’s dimensions or the guide roll’s position change, the ring’s outer diameter and the displacement of the measuring roll will no longer meet the original linear relations, as shown in Fig. 5.
Table 2 FE models for training and test samples for NN model


Fig. 4 Formed rings with unqualified shape in FE simulation:
As previously mentioned, unstable rolling will cause the displacement value of the measuring roll to be fluctuant, and then the measured value of the ring’s dimensions is incorrect. For example, the rolled ring’s shape becomes elliptic during the VHRR process, as shown in Fig. 4(b). When the measuring roll contacts the ring in the direction of ellipse’s short axes,thedisplacement value of the measuring roll will be smaller, and measured value of the ring’s dimensions will be correspondingly smaller than the actual value. On the contrary, the measured value will be larger. The abnormal data (which are marked by the circle in Fig. 5) will affect the training of the NN model, so data eliminating and filtering of the FE simulation results should be executed according to the following standards:
1) The displacement value of the measuring roll should increases continuously as the ring rolling proceeds. If the displacement value of the measuring roll fluctuates severely, that means the roundness of the ring becomes worse, the displacement value of the measuring roll should be filtered or eliminated at this moment.
2) When the fluctuation amount of the displacement value of the measuring roll is greater than 1.5 mm, which means the shape of the ring becomes seriously ellipse, the results of this FE group should not be taken as the data sample.

Fig. 5 Data curves of FE simulations before processing
The partial data curves after processing is illustrated in Fig. 6.

Fig. 6 Data curves of FE simulations after processing
2.2 Establishment of soft measurement model based on RBFNN
After accomplishing the data acquisition and processing, the soft measurement model of the ring’s dimensions based on the RBFNN is established in MATLAB software. During vertical hot ring rolling (VHRR) process, the parameters, ring blanks (D0, d0), the guide roll’s position (Gx, Gy), and the displacement of the measuring roll and drive roll (Sm and Sd), are independent of each other and do not exist coupling effects during VHRR process, so these parameters are chosen as the input factors of the NN model. Figure 7 shows the structure of the NN model. Assuming that Wki represents the output weight matrix. fi(X-Xi) represents the radial basis function of hidden layer, b2k represents the output bias vector and Xi=(x1, x1, …, xh) represents the center vector of the radial basis function, so the kth output can be expressed by [12]
 (3)
(3)

Fig. 7 Structure of soft measurement NN model of ring’s dimensions
Gaussian function is usually adopted as the radial basis function:
 (4)
(4)
where ||X-Xi|| represents the Euclidean distance between input vector and the center vector. b1i represents the bias vector of hidden layer.
As mentioned above, the FE model has taken into account of thermal mechanical coupling. That is to say, the data, which are used for training and testing the NN model, are acquired from the 3D coupled thermo- mechanical FE model for VHRR, so the thermo- mechanical coupling effects should be indirectly considered in NN model. Through training the NN model with a large amount of data, the parameters of NN model Xi, b1i, Wki and b2k can be obtained. By substituting the parameters into Eqs. (3) and (4), the relations between output vector Y (Dt and dt) and input vector X (D0, d0, Gx, Gy, Sd and Sm) can be set up.
The result data of 34 groups of FE model (There are 490 data samples after data processing) are used for training the NN model. Considering that the soft measurement NN model should meet the accuracy requirement for practical VHRR process and should also has good generalization ability to different VHRR situations. The mean squared error (EMSE) of the model is set to be (1-3)×10-7. Figure 8 shows the variation curve of the training process. After NN training, the kernel number of the NN model’s hidden layer is determined to be 15, that is to say, the NN structure is 6×15×2. The NN model parameter can be also obtained corresponding to the minimum value of EMSE of the model (EMSE is calculated to be 1.48704×10-7), which are listed in Table 3. The comparison between the RBFNN model’s calculation results and FE simulation results is illustrated in Fig. 9. It can be seen that both of their values are in good agreement.

Fig. 8 Variation curve of RBFNN training process
To analyze the calculation accuracy of the soft measurement NN model quantitatively, the residual errors between the soft measurement NN model’s calculation values and FE simulations are also studied, as indicated in Fig. 10. It can be seen that the range of residual error is from -0.837 to +0.946 mm. The residual errors of the NN model are within ±1.0mm and the residual errors within ±0.5 mm accounting for 89.18% of the whole data sample. Generally speaking, in practical VHRR production, the dimensional tolerance of the ring products whose outer diameter is 500 mm should be within ±(1-2) mm [6]. So, the soft measurement NN model of the ring’s dimensions meets the accuracy requirements of practical production.
3 Soft measurement model based on GA- RBFNN
To improve the model’s calculation accuracy and generalization ability, the genetic algorithm (GA) [15] is introduced to optimize the structure parameters (Xi, b1i, Wki and b2k) of RBFNN model.

Fig. 9 Comparison between RBFNN model’s calculation values and FE simulations for training samples
3.1 Algorithm of GA-RBFNN
The algorithm flow of GA-RBFNN is shown in Fig. 11.
1) Initialization of data sample. The data processing is accomplished as illustrated in Section 2.2.
2) Initialization of the parameters in genetic algorithm. The optimization variables are set as the Xi, b1i, Wki and b2k. Initial values are given to these variables according to those obtained from the training of RBFNN.
3) Construction of the fitness function. The reciprocal of the quadratic sum of the residual errors between the soft measurement NN model’s calculation values and FE simulation results is selected as the fitness function, and the fitness value of individuals can be calculated by [15]
 (5)
(5)
where N is the sample size; YNN(i) is the output value of the ith sample of RBFNN; YFE(i) is the FE simulation results of the ith sample.

Fig. 10 Residual errors of RBFNN model for training samples

Fig. 11 Algorithm flow of GA-RBFNN
4) Selection, crossover and mutation
The Roulette selection method is utilized. The selection probability Pj of the jth individual is proportional to its fitness value, which can be computed by
 (6)
(6)
where fj is the fitness value of the jth individual; S is the population size. The cumulative probability Qj of the jth individual is given by Eq. (7). Then, a random number r is generated in [0, 1]. If r1, the first individual will be selected; else if Qj-1≤rj, the jth individual will be selected:
 (7)
(7)
Crossover adopts the simulated binary crossover method. Two individuals x1 and x2 are chosen from the parent population, and the new generations are generated with linear combination crossover as expressed by [15]
 (8)
(8)
where α is a random number. Assuming the crossover probability is PC, when PC>α, the crossover can be operated to generate the new generations y1 and y2.
Mutation adopts the uniform mutation method. One individual x=[v1, v2, …, vm] is randomly selected from the parent population, and then a component vk is randomly selected from x. Another component  ak+
ak+ which is randomly selected in [ak, bk] according to uniform probability, is instead of vk, and then the new mutant individual
which is randomly selected in [ak, bk] according to uniform probability, is instead of vk, and then the new mutant individual 
 is generated.
is generated.
5) Iteration stopping criterion. Determine whether the fitness value satisfies the precision requirements, or the genetic algebra reaches the preset value. If so, the iteration will be stopped and the optimized parameters of RBFNN are deduced. If not, the next selection, crossover and mutation will continue.
The structure parameters of GA-RBFNN model are listed in Table 3. By substituting their values into Eqs. (3) and (4), the expressions of the soft measurement NN model of ring’s dimensions can be derived.
Figure 12 shows the residual errors between the GA-RBFNN model’s calculation values and FE simulation results. It can be seen that the range of residual error is from -0.873 to +0.889 mm, and the residual errors within ±0.5 mm accounts for 91.02%, which is superior to that of RBFNN.
3.2 Comparison of test results between RBFNN model and GA-RBFNN model
To confirm the reliability of the soft measurement NN model, the VHRR FE models in which the ring blanks’ dimensions are D0=250 mm, d0=120 mm and the guide roll are at several different positions, as illustrated in Table 2, are established. In addition, the conditions whose ring blanks’ sizes are the same with those of the training samples, but the positions of the guide roll are different (List in Table 2) are also simulated to test the soft measurement NN model. 94 data samples are acquired from the simulation results based on the method mentioned in section 2.2. The trained NN model is tested using the 94 data samples. The calculation values and the residual errors of RBFNN model and GA-RBFNN model are obtained, as shown in Figs. 13-16. It can be seen that the residual errors of the two NN models are within ±1.0 mm, that is, the calculation accuracy of the soft measurement NN model can satisfy the practical requirement of 500±(1.0-2.0) mm. For RBFNN model, range of residual error is from -0.9901 to +0.8901 mm, and the residual errors within ±0.5 mm accounts for 71.28% of the whole data sample. While for GA-RBFNN model, the range of residual error is from -0.5437 to +0.8458 mm, and the residual errors within ±0.5mm accounts for 88.30%, that is, the calculation accuracy of the GA-RBFNN model is higher than the RBFNN model. The above analysis shows that the soft measurement NN model of the ring’s dimensions is applicable to VHRR process with other different ring blank sizes and guide roll’s positions.
Table 3 Structure parameters of GA-RBFNN model


Fig. 12 Residual errors of GA-RBFNN model for training samples

Fig. 13 Comparison between calculation values of RBFNN model and FE simulations for test samples

Fig. 14 Residual errors of RBFNN model for test samples

Fig. 15 Comparison between calculation values of GA-RBFNN model and FE simulations for test samples

Fig. 16 Residual errors of GA-RBFNN model for test samples
4 Experimental verification of soft measurement NN model of ring’s dimensions
The VHRR experiments were conducted on D51-350NC VHRR mill which is developed by Wuhan University of Technology (Wuhan, China) to validate the soft measurement NN model of the ring’s dimensions. The parameters of this mill are listed in Table 4. The on-line soft measurement system of ring’s dimensions for VHRR process is composed of two displacement sensors, data acquisition instrument and a computer, as shown in Fig. 17. Two displacement sensors are installed at the sliders of the drive roll and the measuring roller, respectively, to observe the displacement of drive roll and measuring roll. The structure parameters’ values of GA-RBFNN model (Table 3) were substituted into Eqs. (3) and (4), and then developed them into the monitoring software using C programming language on computer.
Table 4 Parameters of D51-350NC VHRR mill

The pure lead was used as the ring blank material, mainly because:
1) On one hand, the macro deformation law of VHRR has been studied and reported in many research [5-8]; on the other hand, the ring’s material has little influence on the measurement results during VHRR process.
2) The real-time measurement parameters are the ring’s hot state dimensions during VHRR process. The dimension change of the cooling ring products after the VHRR process is not considered.
3) The ring rolling process can be suspended without regard to the temperature decrease. Moreover, it is convenient to gain more measurement data artificially to verify the soft measurement model.
The conditions of VHRR experiment are as follows:
1) D0 and d0 of the ring blank are 240 mm and 120 mm, respectively;
2) Three lead ring blank samples are manufactured by casting method, and the casting die is shown in Fig. 18.
3) The coordinate of guide roll is (199.13, -21.32).
Before ring rolling process, the dimensions of ring blanks D0, d0, the coordinate values of guide roll (Gx, Gy) were inputted into the software. During ring rolling process, the displacement values of drive roll and measuring roll were gathered through data acquisition instrument, and then the ring’s dimensions Dt and dt were calculated by the soft measurement model on-line, simultaneously, and five different feed amounts were set when one ring blank was rolled. The values of the ring’s outer diameter Dt, and inner diameter dt were measured artificially at intervals between two feeding periods to verify the soft measurement model. Figure 18(c) shows the formed rings. The VHRR process of both FE simulation and experiment is shown in Fig. 19. It is observed that the process of experiment is consistent with that of the simulation.
The experimental data are listed in Table 5. It can be seen that the calculation results of ring’s dimensions of both RBFNN model and GA-RBFNN model are close to the artificial measurement data. The analysis on the residual errors of the NN models are conducted, as shown in Fig. 20. For RBFNN model, the range of residual error is from -1.5624 to +1.3215 mm. While for GA-RBFNN model, the range of residual error is from -0.76997 to +0.7694 mm.

Fig. 17 D51-350 NC VHRR mill and on-line soft measurement system

Fig. 18 Ring blank and formed rings:

Fig. 19 VHRR process of FE simulation and experiment:
Table 5 Comparison between artificial measurement data and calculation results of NN models (D0=240 mm, d0=120 mm)


Fig. 20 Residual errors between results of NN models and artificial measurement data
5 Conclusions
1) A soft measurement model of ring’s dimensions is established based on RBFNN. The training and test are conducted by the data samples obtained from the VHRR FE simulations, and then the structure parameters of the soft measurement NN model are obtained.
2) The genetic algorithm is introduced to optimize the structure parameters of RBFNN model. Through comparison the calculation values between RBFNN model and GA-RBFNN model, it is found that the residual errors of two NN models are within ±1.0mm, but the calculation accuracy of GA-RBFNN model is higher than the RBFNN model.
3) The on-line soft measurement system of ring’s dimensions for VHRR process is set up. The VHRR experiments were conducted to validate the soft measurement NN model of the ring’s dimensions. During the VHRR experiments, the ring’s dimensions were measured artificially and calculated by the soft measurement NN model on-line. The calculation values of GA-RBFNN model are close to the artificial measurement data, and the range of residual error of GA-RBFNN model is from -0.76997 to +0.7694 mm, which satisfies the practical requirement.
References
[1] HUA Lin, HUANG Xing-gao, ZHU Chun-dong. Theory and technology of ring rolling [M]. Beijing: Mechanical Industry Press, 2001: 1-20. (in Chinese)
[2] LEE K H, KIM B M. Advanced feasible forming condition for reducing ring spreads in radial-axial ring rolling [J]. International Journal of Mechanical Sciences, 2013, 76(11): 21-32.
[3] HIRT G, KOPP R, HOFMANN O, FRANZKE M, BARTON G. Implementing a high accuracy multi-mesh method for incremental bulk metal forming [J]. CIRP Annals-Manufacturing Technology, 2007, 56(1): 313-316.
[4] LEE K H, KO D C, KIM D H, LEE S B, SUNG N M, KIM B M. Control method for centering rolls in radial-axial ring rolling process [J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(3): 535-544.
[5] GUO Liang-gang, YANG He. Towards a steady forming condition for radial-axial ring rolling [J]. International Journal of Mechanical Sciences, 2011, 53(4): 286-299.
[6] HAN Xing-hui, HUA Lin, ZHOU Guang-hua, LU Bo-han, WANG Xiao-kai. A new cylindrical ring rolling technology for manufacturing thin-walled cylindrical ring [J]. International Journal of Mechanical Sciences, 2014, 81: 95-108.
[7] ZHOU Guang, HUA Lin, LAN Jian. FE analysis of coupled thermo- mechanical behaviors in radial-axial rolling of alloy steel large ring [J]. Computational Materials Science, 2010, 50(1): 65-76.
[8] KIM N, KIM H, JIN K. Optimal design to reduce the maximum load in ring rolling process [J]. International Journal of Precision Engineering and Manufacturing, 2012, 13(10): 1821-1828.
[9] ALLWOOD J M, MUSIC O, RAITHATH A, DUNCAN S R. Closed-loop feedback control of product properties in flexible metal forming processes with mobile tools [J]. CIRP Annals- Manufacturing Technology, 2009, 58(1): 287-290.
[10] WANG Xiao-kai, HUA Lin. On-line measurement method for various guide modes of vertical ring rolling mill [J]. Measurement, 2011, 44(4): 685-691.
[11] PARVIZI A, ABRINIA K. A two dimensional upper bound analysis of the ring rolling process with experimental and FEM verifications [J]. International Journal of Mechanical Sciences, 2014, 79: 176- 181.
[12] LI Wei-guo, YU Qian, LUO Ri-cheng. Application of fuzzy analytic hierarchy process and neural network in power transformer risk assessment [J]. Journal of Central South University, 2012, 19(4): 982-987.
[13] WANG Xiao-kai, HUA Lin, HAN Xing-hui, WANG Xiao-xuan, WANG De-hui, LIU Ya-li. Numerical simulation and experimental study on geometry variations and process control method of vertical hot ring rolling [J]. International Journal of Advanced Manufacturing Technology, 2014, 73(4): 389-398.
[14] YIN Fei, HUA Lin, MAO Hua-jie, HAN Xing-hui. Constitutive modeling for flow behavior of GCr15 steel under hot compression experiments [J]. Materials & Design, 2013, 43(1): 393-401.
[15] CAO Jian-guo, XU Xiao-zhao, ZHANG Jie, SONG Mu-qing, GONG Gui-liang, ZENG Wei, Preset model of bending force for 6-high reversing cold rolling mill based on genetic algorithm [J]. Journal of Central South University of Technology, 2011, 18(5): 1487-1492.
(Edited by YANG Bing)
Cite this article as: WANG Xiao-kai, HUA Lin, WANG Xiao-xuan, MEI Xue-song, ZHU Qian-hao, DAI Yu-tong. Soft measurement model of ring’s dimensions for vertical hot ring rolling process using neural networks optimized by genetic algorithm [J]. Journal of Central South University, 2017, 24(1): 17-29. DOI: 10.1007/s11771-017-3404-1.
Foundation item: Project(51205299) supported by the National Natural Science Foundation of China; Project(2015M582643) supported by the China Postdoctoral Science Foundation; Project(2014BAA008) supported by the Science and Technology Support Program of Hubei Province, China; Project(2014-IV-144) supported by the Fundamental Research Funds for the Central Universities of China; Project(2012AAA07-01) supported by the Major Science and Technology Achievements Transformation & Industrialization Program of Hubei Province, China
Received date: 2015-09-14; Accepted date: 2016-05-11
Corresponding author: HUA Lin, Professor; Tel: +86-27-87653249; Fax: +86-27-87168391; E-mail: wxk0919@163.com,wxk0919@whut.edu.cn