J. Cent. South Univ. (2018) 25: 903-918

DOI: https://doi.org/10.1007/s11771-018-3793-9

Bi-level hybrid local search approach for three-dimensional loading problem with balancing constraints

ZHU Xiang(朱向)¹, LEI Ding-you(雷定猷)²

1. Department of Economics and Management, Hunan Women’s University, Changsha 410004, China;

2. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: This paper presents a bi-level hybrid local search (BHLS) algorithm for the three-dimensional loading problem with balancing constraints (3DLP-B), where several rectangular boxes with even densities but different sizes are loaded into a single cubic bin to meet the requirements of the space or capacity utilization and the balance of the center of gravity. The proposed algorithm hybridizes a novel framed-layout procedure in which the concept of the core block and its generation strategy are introduced. Once the block-loading sequence has been determined, we can load one block at a time by the designed construction heuristic. Then, the double-search is introduced; its external search procedure generates a list of compact packing patterns while its internal search procedure is used to search the core-block frames and their best distribution locations. The approach is extensively tested on weakly to strongly heterogeneous benchmark data. The results show that it has better performance in improving space utilization rate and balanced condition of the placement than existed techniques: the overall averages from 79.85% to 86.45% were obtained for the balanced cases and relatively high space-usage rate of 89.44% was achieved for the unbalanced ones.

Key words: 3D loading; balancing constraints; framed layout; bi-level hybrid local search; core block

Cite this article as: ZHU Xiang, LEI Ding-you. Bi-level hybrid local search approach for three-dimensional loading problem with balancing constraints [J]. Journal of Central South University, 2018, 25(4): 903–918. DOI: https://doi.org/10.1007/s11771-018-3793-9.

1 Introduction

As an important application in industrial sectors, the three-dimensional loading problem (3DLP) aims to obtain high space utilization when selecting and packing a number of boxes into a bin orthogonally. The boxes are rectangular items with even density and different lengths, widths, and heights, while the bin is a cube with specified available space and carrying capacity. Each box can have at most six permitted packing orientations or rotation variants. Due to its characteristics of complex combinatorial optimization, the 3DLP is a typical NP hard problem [1].

The loading problem with balancing constraints is one of the important problems in optimization studies and shipment practice [2], where some rectangular boxes with even densities but different sizes are loaded into a single cubic bin to meet the requirements of the space or capacity utilization and the balance of the center of gravity. In this problem, balanced conditions are ensured by minimizing the difference between the overall center of gravity (CG) and the desired CG. In addition to the basic constraints such as the packing capacity, the placement orientation of boxes and no two shapes overlap, the paper will focus on the three-dimensional loading problem with balancing constraints (3DLP-B) and optimize its comprehensive goals involving the space utilization and balancing condition.

In the transportation with train, fleet and airplane, the weight distribution is an important condition for the freight packing. It is significant for the safety of the cargo and instruments, saving energy consumption during transportation, and speeding up the operating processes of loading and unloading. Unbalancing weight distribution will harm to the vehicle and even lead to the accident. The loaded plane will consume more energy if its CG is not kept in the appointed domain. Improper freight placement in the fleet will produce extra operation of loading and unloading on the delivery. How to improve the space utilization and the balance level of the placement is a general issue for the shipment practice.

2 Literature review

2.1 Related work to 3DLP

As the 3DLP is an important issue in the practice of shipment, it attracts a number of researches and brings about diversity methods. Summing up the researches, there are several categories of methodologies for the 3DLP: exact methods, constructive heuristics, metaheuristics strategies and tree-search methods.

Since 3DLP is known to be NP hard, to date, only a few exact methods have been suggested in the literature. When it comes to the container loading problem (CLP), CHEN et al [3] and PADBERG et al [4] propose integer programming methods, and MARTELLO et al [5] develop an exact branch-and-bound method. VANCROONENBURG et al [6] use the MIP model to solve a specific 3D packing problem related to the cargo loading space problem with limited scale.

The nature of the 3DLP seems to make it suitable for constructive heuristics in which the loaded items are firstly gathered into groups, and then gradually packed into a space with the conduction of an iteration or search mechanism. GEHRING et al [7] propose a tower- arrangement approach where the packing units were generated with different types of boxes. There have also been wall-building approaches [8] where vertical layers constructed by heuristics were filled into a bin and combined in the longest dimension of the bin, and layer-building approaches [9] where the bin is filled from the bottom up using horizontal layers. The best-performing approaches in the recent literature share similar algorithm structures and can be classified as block-building approaches [10, 11]. A block is a subset of boxes that is placed compactly inside its minimum bounding cuboid. Each step of the approach involves placing a block into some free space in the bin until no more blocks need to be packed.

Metaheuristics search strategies have been the preferred method in the last 10 years. These include the tabu search approaches (TS) of LIU et al [12] the genetic algorithms (GA) of GEHRING et al [7] and JOSE et al [13]. Meanwhile, some parallel search or co-evolutionary mechanisms have also been exploited for the packing problems, for example, the parallel or hybrid search algorithm of MACK et al [14], the parallel island- based multiobjectivized memetic algorithm of SEGURA et al [15]. Tree-search methods or graph- search methods were considered as other categories of solution methods by FANSLAU et al [16].

2.2 Related work to 3DLP-B

Meeting the balancing conditions in a stowage plan is significant for the container transport, as well as for the general shipping facilities. GEHRING’s stack [7], DAVIES’s wall [10], and ELEY’s block [11] are typical item constructive patterns where the freight units remain intact and good weight distributions are achieved by the swapping or shifting of the units’ positions. BALDI et al [17] introduce a 3D aircraft knapsack problem MIP model to maximize the packed items’ priority with balancing constraints. A heuristic based on the update of the items sequence is used to search the optimization placement. QUEIROZ et al [18] deal with the strip packing problem under two practical situations: the packing with load balancing and multi-drop constraints, the packing with load balancing and load bearing constraint. ZHU et al [19, 20] address to the loading problems with concentrated-weight and axle weight constraints, respectively, and some heuristics are designed for them. With the consideration of the reality operation, the time constraint is also integrated into the loading problem by ZHU et al [21] and a phased approach is used to simplify it.

Some studies involve the framed-layout conception in which, before a detailed arrangement is implemented, an initial placement frame with the function to affect the overall balance level of the packing is generated. With regard to railway freight loading, LEI et al [22] put forward a constructive approach to determine the generation of the item units and their distribution locations. Based on a cooperative co-evolutionary algorithm, TENG et al [23] propose a dual-system framework to deal with a satellite-module layout design which can also be seemed as a special packing problem with balancing constrains.

3 Bi-level hybrid local search algorithm

3.1 Overview

Surveying the recent studies, the framed- layout approach is regarded as an efficient method for the 3DLP-B. It presumes that in any balanced placement pattern, there are some items units which can regulate or control the balance level of the placement. If the units and their location are determined, we can determine an initial frame for the layout, based on which the remainder of items will be gradually packed and the whole problem will be simplified. However, it is not easy to directly acquire a well-balanced frame for all kinds of cases. LEI et al [22] construct the core stacks according to the freights sizes and densities to build an initial layout skeleton. But the gained skeletons lack diversified combinations. TENG et al [23] design a dual-system co-evolutionary model: one system constructs the layout frame, while the other is used to produce a diversified packing pattern; and an optimization design is generated through the co-evolution of the two systems. But the approach is not suitable for weakly coupled systems and cannot be used for the 3D loading problem directly. MACK et al [14] studied the effect of the transmission of solutions in the parallel search mechanism and concluded that the improvements brought about by the communication of solutions during the search process were no better than that when this was done at the end of search phase, while the latter is easier to implement.

According to the category characteristics of loading objects, the 3DLP can be divided into weakly heterogeneous and strongly heterogeneous instances [10]. Different objects’ attribute distributions will affect the selection of the loading approaches and bring different placement results. It becomes an important clue for the design of the packing procedure in this paper. According to the framed-layout philosophy, this paper proposes a double layer hybrid local search algorithm (BHLS) which integrates the constructive heuristic into simulated annealing or a tabu search for the 3DLP-B. Firstly, block units are built by the block generation approaches in line with box attributions. They are packed one by one under the guidance of the constructive heuristic and the packing sequence provided by the external search of BHLS. Then some packing patterns with a relatively high space utilization rate will be acquired. Secondly, the core units extracted from these patterns are recombined with non-core ones then packed with the internal algorithm of BHLS. It may result in a well-balanced placement scheme under this condition of unit combination. Lastly, through comparing the values of the objective functions of the obtained schemes, the best placement found will be exported as the final solution. Since the second phase search is based on the first stage search and the search space of the latter is contained in the space of the former, our approach is an integration approach and can be defined as a bi-level hybrid local search. The general scheme of the BHLS algorithm is depicted in Figure 1.

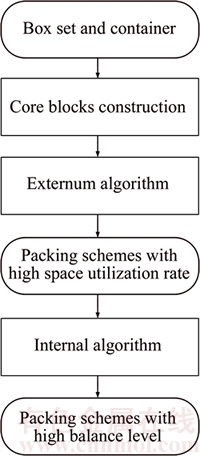
Figure 1 General scheme of BHLS

3.2 Constructive heuristic

3.2.1 Packing unit construction

In the constructive heuristic (CH), packings are constructed by placing one unit (block or box) at a time until no more boxes can be loaded. However, different structures of these units will bring about distinct packings.

In the study of the container loading problem, the packing units can be divided into two basic structures: simple and composite. The wall and layer usually built with the identical type of boxes can be regarded as a simple construction. And the tower and block built with different types of boxes are classified as the composite construction. In line with the differences of the boxes’ attributes such as size, mass, and density, the loaded items can be divided into weakly heterogeneous and strongly heterogeneous instances, and are adapted for distinct construction units as well [24]. On one hand, the weakly heterogeneous instance is adapted to simple constructions; the strongly heterogeneous instance favours a composite one. On the other hand, the simple structure is more common in loading and shipment practice, where distinct types of freight need to be packed separately. In our paper, a block-building approach which is suitable for both the weakly and strongly heterogeneous cases is proposed. After presenting the algorithms used to produce the simple and general blocks, we will introduce a novel concept of core blocks and their generation tactics.

1) Simple block construction

We define the boxes with identical sizes and mass as the homogeneous boxes. A simple block is made up of homogeneous boxes with identical packing orientations. There are no gaps between the boxes, which are stacked into a cube (Figure 2(a)). The generation algorithm for the simple blocks is presented in Figure 3.

2) General block construction

As a composite structure, a general block consists of heterogeneous boxes or homogeneous boxes with distinct packing orientations (Figure 2(b)). It can be regarded as the combination of several simple blocks along three dimensions of the x, y and z axes. Some generated blocks must be discarded if they violate the basic constraints or contain many gaps which can result in low space utilization. So we provide the conditions for the general blocks created:

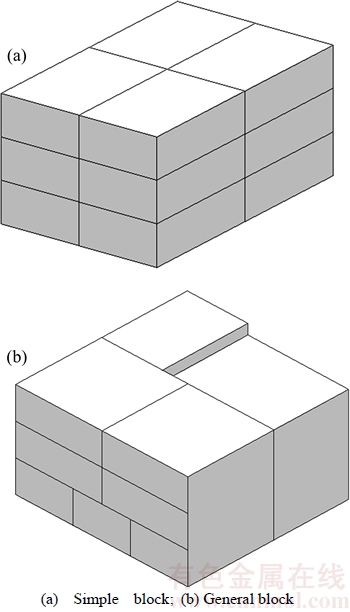
Figure 2 Classes of blocks:

Figure 3 Pseudo-code of generation algorithm for simple blocks

(1) The generated blocks never surpass the boundary of the bin.

(2) Each general block can be represented by its circumscribed cuboid C, and then the filling ratio in C is no less than L.

(3) In order to satisfy the stability conditions, the ratio of the top area of the general block to the top area of C should be no less than R.

(4) Blocks with the same three dimensions, boxes included, and packable rectangular top region are treated as identical blocks. And only one representation is used.

(5) To facilitate the follow-up loading, the complexity of the generated block will be regulated: the maximum allowed number of the simple-block types contained in a general block is C_M.

(6) The generated blocks that satisfy the (1)–(5) conditions belong to the legal ones. And we specify the maximum number of the legal blocks generated as N_B.

Based on the simple blocks set BL₁ and considering these regulations, we can employ the algorithm in Ref. [25] to generate the general blocks set BL₂ (Figure 4).

Figure 4 Pseudo-code of generation algorithm for general blocks

3) Core block selection

When a framed layout approach is used, we need to select some box units, called core blocks, to constitute the packing framework (the dotted line area in Figure 5). The core blocks set, represented as BL_c, consists of a batch of general or simple blocks which can determine the overall balance situation or adjust the location of CG. Generally speaking, the types of the boxes with higher density, smaller size and less total quantity are the ideal ones to build the core blocks. They can regulate or control the balance situation and leave more remaining space for further packing. However, due to the difference of the boxes’ attributes, the ideal condition is often difficult to meet. We often need to select the core blocks in line with the attributes of blocks in some specific packing patterns.

When it comes to the strongly heterogeneous instances, there are great differences of the attributes in different types of boxes. We just need to confirm the core blocks as the ones contained the boxes with higher densities or masses. But with regard to the weakly heterogeneous instances, there are not obvious differences of the attributes in the boxes. The core blocks are determined according to the blocks’ attributes in the packing pattern. The process for generating the core blocks is presented in the following.

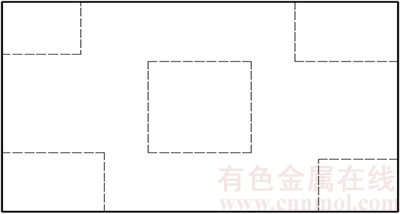
Figure 5 Core blocks distribution

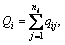
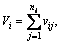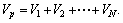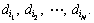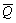Let N be the total number of unique box types, then q_ij, v_ij and d_ij are respectively the mass, volume, density of box b_ij. Let n_i, Q_i and V_i be the quantity, the sum of masses and volumes of box type b_i. Then and the total volume of all boxes is According to the densities, all boxes are ranked in descending order to produce an box array Let and 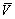be the maximum allowed weight and volume of the boxes packed in the bin, and Q_e and V_e be the maximum mass and volume of the boxes required to be loade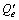d, and 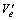are the maximum estimations of the mass and volume of the boxes which could be loaded. 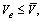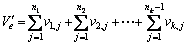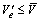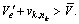Ifthen let else let (where n_k represents the n_k th piece of the kth type in the array produced), which can meet the criteria and If 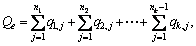then the upper bound of the packing capacity is 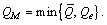Let Q_c be the total mass of all the core blocks. In the light of the balance principle, it should be equal to or greater than the total mass of the non-core blocks. That means that if 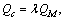where 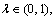λ should be theoretically equal to or greater than 0.5. In actual operation, we can select distinct values of λ according to the attributes of the boxes in different instance groups: λ<0.5 for the strongly heterogeneous instances and λ≥0.5 for the weakly heterogeneous instances. Accordingly, two distinct tactics for selecting core blocks are proposed.

Tactic 1. In the packing patterns constituted by the strongly heterogeneous boxes, the balance situation is dominated by the boxes with higher density, which we define as core elements and present as a set F_c. The blocks produced by the generation algorithms and containing core elements are regarded as core blocks, whose number is small but sufficient to decide the overall balance situation. The process of determining the core elements and blocks for strongly heterogeneous instances is introduced in the following.

All box categories are ranked in descending order by the densities, and those with the same density are ranked in ascending order in accordance with the box quantity contained in each type. Select the first N_S1 (N_S1=λN+1) classes and define the array

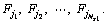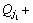
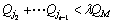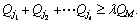obtained asDetermine j_t according to the order of the sequence to meet and Then 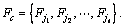The blocks containing the elements in F_c are the core blocks which will make up an array 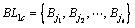accordingly.

Tactic 2. Since generally there are not core elements in the weakly heterogeneous instances as in the strongly heterogeneous ones, the core blocks can be determined by the characteristics of the related blocks in the special placement. First, we calculate the total mass 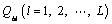for each block. All the blocks are ranked in descending order according to Q_bl. Selecting the preceding blocks and ranking them in descending order according to the joined density 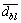(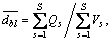where Q_s and V_s are the mass and volume, respectively, of the sth box in block bl), a new blocks sequence 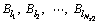is generated. We determine l_t to meet the criteria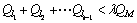and 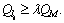So the final core blocks combination array derived from the packing pattern will be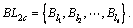

3.2.2 Selecting packing space

The empty maximal-spaces (EMSs) approach [26] is used to represent the residual available space in the loading process. When a block is loaded into one corner of a packing space, the residual space will be divided into three crossover subsidiary parts (the transparent cubes of Figure 6), each of which corresponds to the maximal expansion space. Two distinct space divisions for results with and without full support from below are respectively presented in Figure 6(a) and of Figure 6(b). Our approach mainly involves the full stability packing condition in which each block is completely supported from below.

The subsidiary spaces produced in the packing process are stored in a spatial list S_l which should be updated according to the following rules. The packing process is successively implemented for each part of the space based on a certain order. Each time, a space is chosen from the space list in which the EMSs are ranked based on the anchor-corner concept [24]. In Figure 7, connecting each corner of a maximal-space S with the opposite corner of the bin C, there exist eight pairs of corners 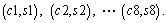We only need to take into account four of them located at the bottom of the bin and select one as the placement position each time. Let (x_i1, y_i1, z_i1) and (x_i2, y_i2, z_i2) (i=1, 2, 3, 4) be the coordinates of the corners of S and C, and be the Manhattan distance (MD) of the corner pairs. The corner of S with minimum MD is defined as the space anchor- corner and the corresponding distance is its anchor-distance. We prefer the space with the smallest anchor distance. If there are more than two minimum distances, the space with the larger volume has priority. Based on these roles, the boxes can be packed from the sides to the centre of the bin, which make the surrounding layout compact, and the empty fragments are gathered in the centre of the bin. This is beneficial to improve the space utilization and the balance conditions.

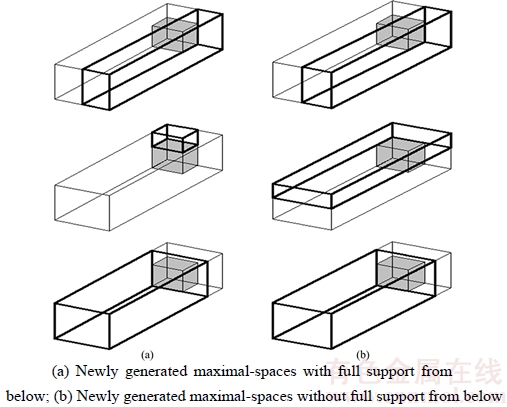
Figure 6 Example of two different dividing processes:

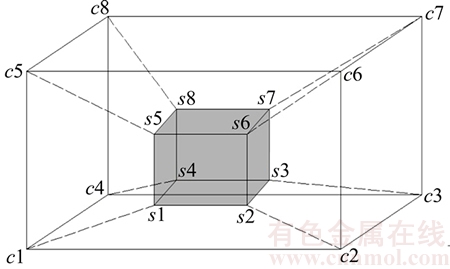
Figure 7 Corner distances between a maximal-space and bin

3.2.3 Selecting placement direction and type

After selecting the loading position, we should also determine the orientation and type of placing further. Without involving the limitation of place orientations of the boxes, there exist at most six placing types for a block by 90° rotation. A best-fit rule is used to determine the placing orientation for a block at the selected location. For each feasible placing orientation, we calculate the distances from the block faces to their opposite bin-wall. And they are ranked in descending order and stored in a vector. The placing orientation is selected in line with dictionary-order. In Figure 8, there are two placing orientations for a block where the height of the block is equal to that of the bin. The calculated distance vectors of the two placing types are (0, 1, 7) and (0, 2, 6) respectively. In the light of the above rule, the placement of Figure 8(a) is selected.

Furthermore, for the general block composed of different boxes with the CG deviating from the geometrical centre, we should consider the impact of its different CG positions on the overall CG site. Based on each type of the above six loading orientations, if the block is rotated along three central axes of each group of block faces, we will get at most four distinct CG positions in the space, which we call “packing types ”(in Figure 9). They will never affect the space utilization and the follow-up packing, but bring about distinct overall CG sites. The packing type of a block is selected in a random manner in the following algorithm of BHLS.

Furthermore, the rotations of the irregular blocks (L≠100%)may lead to a state that does not take gravity effects into account. That would result in faulty solutions for many real-life applications, so our approach simulates the force of gravity by compacting all boxes along the z axis towards the (x, y) plan.

3.2.4 Total packing procedure

Each time, we select the maximum space from a space list S_l produced by the above rules. After scanning the entire block list BL_l and the available box list C_l, we can determine a feasible block list F_l in which the blocks can be packed into the selected space and the weight of each never surpass the remainder load capability of the bin. Once a packing sequence P_s is generated by the search, a block will be chosen from the F_l according to the specified index of P_s and packed into the appointed space at the kth stage. Then the space list S_l and box list C_l should be updated subsequently. If the feasible block list F_l is empty, then we discard the selected space and take into account the next one in S_l until none of the residual spaces can be further used or all boxes have been loaded. The pseudo- code of the total packing procedure of the construction heuristic (CH) is presented in Figure 10.

Figure 8 Example of two different placement directions:

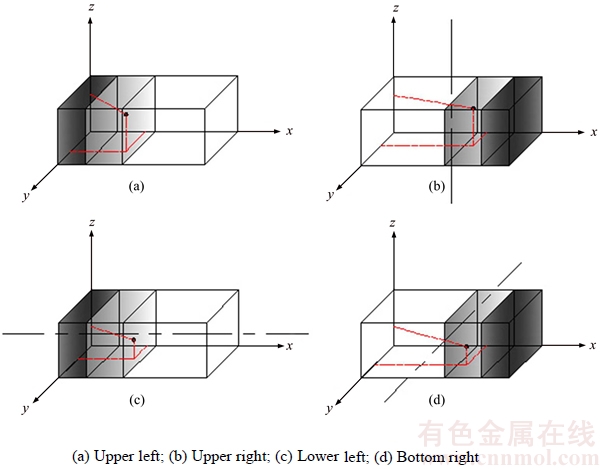
Figure 9 Example of four different placing types with different CG positions:

Figure 10 Pseudo-code of constructive heuristic (CH) procedure

3.3 Bi-level hybrid local search algorithm

On one hand, the packing pattern with a high space utilization rate is both a preferable combination among the boxes but also a favourable matching between the boxes and the bin. On the other hand, the different placements for a batch of boxes might have different core block combinations and their distributions, which may result in distinct use rates and CG positions. Therefore, a bi-level search is proposed to find the core frames and their distributions.

Firstly, the external search procedure of BHLS combining a simulated annealing (SA) algorithm with construction heuristic produces some high space-utilization packing patterns. Secondly, based on these patterns and the selecting tactics, some core blocks with compact shapes and having the function of controlling the position of the overall CG can be derived. They are then incorporated with the non-core blocks to produce new packing sequences and input into the interior search of BHLS. The better locations of different core block combinations and their corresponding packing schemes will be achieved by the interior search of BHLS, which incorporates a tabu search with heuristic construction. Finally, the objective values of the packing schemes are compared to find a better solution.

3.3.1 Encoding and neighborhood structure

In the CH procedure, the packing is implemented based on the packing sequences, each of which, in general, corresponds to a feasible packing scheme. Every element in a sequence signifies a choice for the block during the packing. If CH is used as a mapping function, the packing sequences can be regarded as an encoding of the packing patterns. A search for an optimization arrangement can approximate to a search for packing sequences and the number of the selected block is encoded. And the sequences are expressed as vectors and 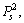respectively, for the external and internal searching. The vector value 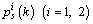indicates the index of the selected block from F_l at the kth stage of packing.

Each time, a residual space is picked out according to the heuristics and load the block with the index appointed by the packing sequences. Different block sequences might result in different placements and the number of stages needed for a complete placement. We empirically regulate the maximum size of the sequences to be S_M. At the later stage of packing, if the index is more than the number of blocks in F_l, we use the modulo operator and its result stands for the index of the block which needs to be packed.

A solution is considered as a neighbour when the corresponding packing sequences differ in exactly one significant index position common to both packing sequences. The large and small two- neighbourhood methods are proposed in work [26]. In order to enable the algorithm to find the global optimum as far as possible, we use the large neighbourhood approach in which the number of a random selected index position K is changed while numbers of other index positions are invariable. Furthermore, as there are a large number of blocks from which to choose, especially in the early search stage, we set the number of the optional blocks at each stage as P_M to control the range of choices and speed up the search.

3.3.2 External search procedure

The SA algorithm is used in the external search due to its excellent global search performance. The parameters t_s and t_f are, respectively, the initial and termination temperatures of SA. The updated number of the sequences for each temperature level is n_t, which will affect the search results under each kind of temperature condition. The number of results produced by the external algorithm can be decided by the annealing ratio ω; the smaller the value of this ratio, the higher the value of the number will be. Meanwhile, the integral variable i_c indicates the generation of the simple block list BL₁ when its value is 0 and the general block list BL₂ when its value is 1. The function 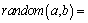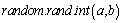can return an integer 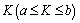with uniform distributions defined in the interval. At the beginning of the search, a vector is regarded as the initial packing sequence, which means the biggest feasible block is selected to pack at each loading stage of the CH approach. The packing plans set LP is output as the final result of the external search of which the pseudo-code is described in Figure 11.

Figure 11 Pseudo-code of external search procedure

3.3.3 Internal search procedure

The internal search of BHLS can be used to determine the better location of the core blocks and corresponding complete placement scheme. The search for the locations of the core blocks can be regarded as the recombination and packing of the core and non-core blocks. The core blocks in the initial sequence of the internal search remain intact while the non-core blocks will be rebuilt based on the remaining boxes. The above two parts will be united to construct a new block set BL’_I and become the base for further searching. Since some box combinations are fixed in the core blocks, the search space of the internal search is smaller than that of the external search, which can speed up the internal search.

According to the tactics for the generation of core blocks, the internal algorithm will extract a core block set BL_Ic (I=1 or 2) from the packing patterns set LP provided by the external search. To avoid the repeat of the search, only when BL_Ic is not contained in the total core blocks set C_set produced can the subsequent procedure be implemented.

At the same time, since the packing sequences of the external and internal searches are respectively structured based on distinct block sets, different sequences might be produced from an identical packing pattern. Therefore, an analysis to the packing pattern and its realization process using new block set BL’_I is required. An example of two packing patterns for a group of blocks with and without balance improvements, respectively, is presented in Figure 12. The block numbers are ranked by their volumes or masses, of which 1, 2, and 3 indicate core blocks, and 4 and 5 indicate non-core blocks. Considering the roles of the heuristic constructive, we can ascertain that the external optimization sequence is (1, 1, 3, 2, 1). That means the No. 1 block is firstly packed and its appointed index is 1. Then the No. 2 block will be ranked as the first one in the remaining boxes and its index will also be appointed as 1. According to the principle, we can generate the whole packed sequence before implementing the balance improvements. Presuming that all the blocks keep the same structures, they will be the items packed by the subsequent internal procedure. To improve the balance level, the sites of 2 and 5 can be swapped and the initial sequence will be changed to (1, 4, 1, 2, 1) accordingly.

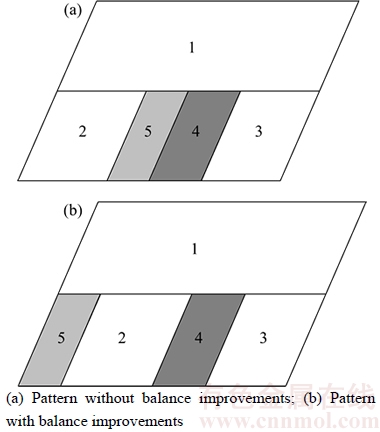
Figure 12 Example of two distinct packing patterns:

Other than the goal of maximizing the space utilization in the external search, the space use and weight distribution are simultaneously considered in the internal algorithm. We can determine the evaluation function for the internal search: 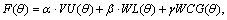where VU(θ) is the space utilization rate, WL(θ) expresses the capacity use rate, WCG(θ) represents the negative value of the CG deviation level and α, β λ are weight coefficients.

A new variable o(k) is introduced to represent the placing types. And the sequence of the internal search becomes a two-dimensional vector 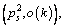which respectively indicates the indexes and the placing types for the selected blocks, while the block placement directions are determined by the heuristic. The value of o(k) is connected with the site of the overall CG of a block and the number of permitted orientations of the boxes included. Supposing the maximum number of the placing type is t_n, and the distances between the overall CG and the space reference corner are ranked in ascending order, the available placing types for each block can be expressed as the numbers from 1 to t_n and selected by a random function.

Owing to its excellent local convergence performance, the tabu search is applied in the internal algorithm. After an initial packing sequence has been determined, the values of the vector can be continuously alternated within an iterative cycle until the search termination criterion is satisfied. And we can search for the optimization distribution locations of the core blocks and the packing scheme, best. By comparing the objective function values of various placements, we will gain the optimization result, Best. The pseudo-code of the internal search is described in Figure 13.

4 Numerical experiments

Empirical studies of the loading problem with balancing constraints are scarce and cannot provide a valid base for comparison and evaluation. After determining the related parameters, the BHLS algorithm is used to solve the 3DLP-B based on the benchmark set. Its validity is demonstrated by the compared and analyzed results of the experiments.

4.1 Experimental environment and test instances

The BHLS algorithm presented is implemented in C/C++ under Windows XP. All computational experiments are carried out on a laptop with a 1.6 GHz Intel(R) Pentium(R) Dual CPU and 2 GB of RAM. The effectiveness of BHLS is tested using the benchmark data set provided by Bischoff and Ratcliff from the OR-library (http://people.brunel.ac.uk/～mastjjb/ jeb/info.html), containing fifteen test classes BR1–BR15, with 100 test instances each. The structure of each problem changes gradually from weakly heterogeneous to strongly heterogeneous according to the decreasing average number of boxes per type. In test class BR1 there are on average 50.15 boxes for each box type, whereas in test class BR15 the average number is only 1.33. A standard ISO-20ft container with a depth of 587 cm, width of 233 cm, height of 220 cm, and gross weight limit of 22 tons is filled. The desired site of the CG for the load in the container is set at the centre of the bottom. Density values of the boxes are generated according to the approach in Ref. [10], where boxes fall into one of two separate categories: either very light or very heavy. The two ranges chosen were (0.01±0.05) and (0.96±1.00) g/cm³ and values were sampled with equal probability from uniform distributions defined in these intervals.

4.2 BHLS configuration

The running of the bi-level algorithm needs the configuration of a serial of parameters including the ones for the constructive of blocks, and the ones for the external and internal searches.

Figure 13 Pseudo-code of internal search procedure

There are four parameters related to the generation of blocks: the maximum number of blocks generated, N_B; the minimum fill ratio of the generated blocks, L%; the minimum area supporting ratio of the blocks, R% and the maximum allowed number of the simple-block types contained in a general block, C_M. As an important parameter in block-building approaches, the maximum number of blocks generated N_B is connected with the traits of test instances. Since most of the researches which involved the block construction based on the benchmark classes BR1–BR15 generate 10000 blocks, and have fully verified its validity [16], we decided on N_B=10000 in our implementation. Furthermore, the number of blocks generated will also be affected by the block fill ratio. MACK et al [14] concluded that the generation algorithm with L=98% has sufficient ability to produce 10000 blocks with compact shapes. We also select the value in our algorithm. C_M can be used to control the number of cycles of the generation algorithm. The more the cycles are, the more the blocks will be generated. ZHANG et al [27] pointed that C_M=5 is a suited choice for the generation of 10000 blocks. Further, since the stability is not the chief consideration in our research, we determined R=96% which is sufficient to meet the general requirement for the loading stability.

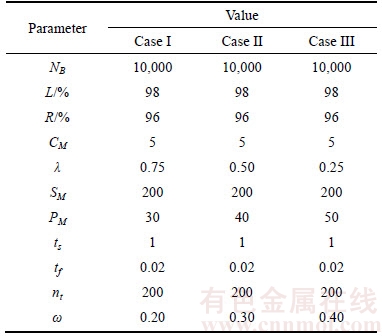
There are also seven parameters of the external and internal searches: the mass bound of the core block combinations, λ; the maximum length of the sequences, S_M; the number of the optional blocks at each stage, P_M; the initial and termination temperatures of SA, t_s and t_f, annealing ratio, ω; the updated numbers of the sequence at each temperature level, n_t. We conducted a small pilot study to obtain the reasonable parameters values. Since many parameters of the algorithm is connected with the difference degree of attributes of the boxes in the cases, we divided the test classes into three groups: I (BF1, BF2, BF3, BF4, BF5), II (BF6, BF7, BF8, BF9) and III (BF10, BF11, BF12, BF13, BF14, BF15). We ran the algorithm over the pilot problem instances sampled from the above three groups respectively, and computed the objective function with different weights values. The parameter combinations with better experiment results are presented in Table 1 and determined as the valid configurations for the experiments.

Table 1 Configurations used on runs in experiments for benchmark cases groups

4.3 Comparative evaluation of proposed approach

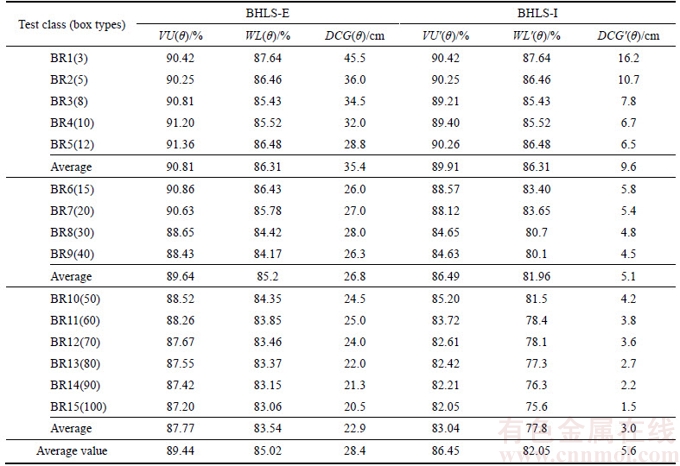
After configuring all the parameters, we ran the algorithm for all the test classes. The average values of the indicators of the optimization placements after the external search (BHLS-E) and internal search (BHLS-I) are presented in Table 2. The weight values, (α, β, γ) for two parts were, respectively, (1, 0, 0) and (0.6, 0.2, 0.2). Meanings of other indicators are identical to preceding definitions.

In Table 2, we can see that the space-use rates for parts of the weakly heterogeneous cases after the internal search are the same as the results of the external search. This means that the ultimate experimental results of these cases might come from the placements of the external search after the adjustment of the centre of gravity. There are also some cases in which the results for the two parts are not identical (the value of the external result, in general, is higher than that of the internal result). This shows that a plan with a higher space-use rate is not necessarily the ultimate scheme and the best solution should be obtained through further searching and comparison.

Based on the benchmark set, DAVIES and BISCHOFF [10] used bar graphs to demonstrate the efficiency of their method in adjusting the CG but did not give further detailed data about each part of the experiments. In that work, average deviation distances for all the cases lie within 35 cm for the container length and 2.5 cm for the width. In our test results, we provide the total deviation distances between CG and the bottom centre of the container. The results for all test cases are no less than 20 cm, the total average distance lies within 6 cm, and parts of the results for the strongly heterogeneous cases are near to 0. Unlike Davies’ approaches, we utilize the heuristic rules in favour of the balanced loading in the initial layout phase. In the balance improvement phase, the position of the CG is changed not only by the recombination and placement of the core and non-core blocks generated but also by the packing based on new block sets, which can effectively expand the search space.

Table 2 Average values of indicators of optimization placements

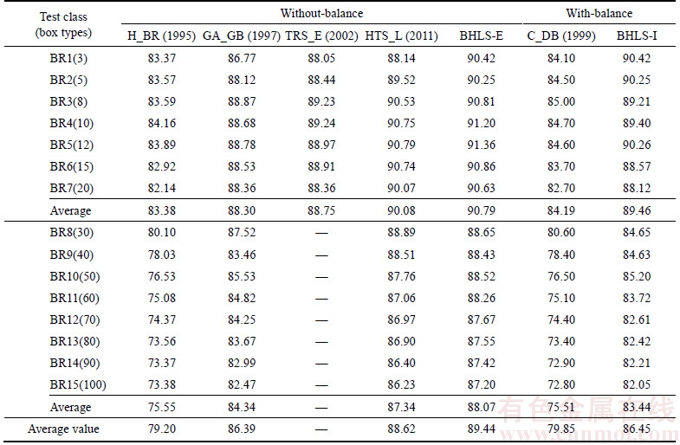
As to the space utilization, BHLS is compared with the following approaches published in the literature and involving the loading problem with weight distribution:

H_BR: the constructive heuristic by BISCHOFF and RATCLIFF [8].

GA_GB: the genetic algorithm of GEHRING and BORTFELD [7].

TRS_E: the tree search approach of ELEY [11].

HTS_L: the hybrid tabu search approach of LIU [12].

C_DB: the composite approach of DAVIES and BISCHOFF [10].

The results in Table 3 are the volume utilizations of different approaches based on the benchmark set and full support constraints. The average optimization results of the external search, or BHLS-E for short, are compared with the results of four approaches without considering the balanced conditions. We can see that the BHLS algorithm has achieved a relatively high space-usage rate. The internal search results, called BHLS-I, are compared with C_DB, the only approach which provided part space-use data with balance constraints. The results of our approach with balance consideration are better than the composite approach.

5 Concluding remarks

1) The three-dimensional loading problem with weight distribution can be well solved based on a framed-layout concept which hybridizes a construction heuristic and a double layer local search. The double search can produce diversified placements while the construction heuristic can improve the efficiency of the search.

Table 3 Average volume utilization for several approaches

2) The different characteristics of the loaded boxes will have an effect on the construction of the packing units and the final search result produced by the designed algorithm. The adjustment of the parameter values of the algorithm for the different instance group is necessary.

3) Computational results on benchmark data show that BHLS has good effectiveness in improving the space or capacity utilization and achieving an even weight distribution. It has improved the overall averages from 79.85% to 86.45% for the balanced cases and achieved relatively high space-usage rate, 89.44% for the unbalanced ones.

4) The computational parameters in our algorithm are selected through a pilot study combined with some empirical methods. With regard to controlling the computational time, we can further study and design some simplified measures such as optimizing the whole search process and adopting more effective heuristics according to the box characteristics.

References

[1] PISINGER D. Heuristics for the container loading problem [J]. European Journal of Operational Research, 2002, 141: 143–153.

[2] ARMOUR D. An FTA best practice guide [M]. Tunbridge Wells: Hilary Kingdom, 2011: 12–17.

[3] CHEN C S, LEE S M, SHEN Q S. An analytical model for the container loading problem [J]. European Journal of Operational Research, 1995, 80: 68–76.

[4] PADBERG M. Packing small boxes into a big box [J]. Mathematical Methods of Operations Research, 2000, 52(1): 1–21.

[5] MARTELLO S, PISINGER D, VIGO D. The three- dimensional bin packing problem [J]. Operations Research, 2000, 48: 256–267.

[6] VANCROONENBURG W, VERSTICHEL J, TAVERNIER K. Automatic air cargo selection and weight balancing: A mixed integer programming approach [J]. Transportation Research Part E, 2014, 65: 70–83.

[7] GEHRING H, BORTFELDT A. A genetic algorithm for solving the container loading problem [J]. International Transactions in Operational Research, 1997, 4: 401–418.

[8] BISCHOFF E E, RATCLIFF M S W. Issue in the development of approaches to container loading [J]. International Journal of Management Science, 1995, 23(4): 377–390.

[9] ARAUJO L J P, PINHEIRO P R. Heuristics backtracking and a typical genetic algorithm or the container loading problem with weight distribution [J]. Communications in Computer and Information Science, 2010, 16: 252–259.

[10] DAVIES A P, BISCHOFF E E. Weight distribution considerations in container loading [J]. European Journal of Operational Research, 1999, 114(3): 509–527.

[11] ELEY M. Solving container loading problems by block arrangement [J]. European Journal of Operational Research, 2002, 141(2): 393–409.

[12] LIU J M, YUE Y. A novel hybrid tabu search approach to container loading [J]. Computers & Operations Research, 2011, 38: 797–807.

[13] JOSE F G, MAURICIO G C R. A parallel multi-population biased random-key genetic algorithm for a container loading problem [J]. Computers & Operations Research, 2012, 39(2): 179–190.

[14] MACK D, BORTFELDT A, GEHRING H. A parallel hybrid local search algorithm for the container loading problem [J]. International Transactions in Operational Research, 2004, 11: 511–533.

[15] SEGURA C, SEGREDO E, LEON C. Parallel island-based multiobjectivised memetic algorithms for a 2D packing problem [C]// Proceedings of 13th Annual Genetic and Evolutionary Computation Conference. Dublin, Ireland, 2011: 1611–1618.

[16] FANSLAU T, BORTFELDT A. A tree search algorithm for solving the container loading problem [J]. Informs Journal on Computing, 2010, 22: 222–235.

[17] BALDI M M, PEROLI G. The three-dimensional knapsack problem with balancing constraints [J]. Applied Mathematics and Computation, 2012, 218: 9802–9818.

[18] QUEIROZ T A, MIYAZAWA F K. Two-dimensional strip packing problem with load balancing, load bearing and multi-drop constraints [J]. Int J Production Economics, 2013, 145: 511–530.

[19] ZHU Xiang, LEI Ding-you, ZHANG Ying-gui. Freights loading optimization with balanced and unconcentrated loading constraints [J]. Journal of Central South University, 2014, 21(8): 3386–3395.

[20] ZHU Xiang, LEI Ding-you. Optimization of freights loading problem with balancing and axle weight constraints [J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(5): 11–17. (in Chinese)

[21] ZHU Xiang, LEI Ding-you, YOU Wei. Optimization of multi-phase variable size bin packing problem with time constraints [J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(4): 157–163. (in Chinese)

[22] LEI Ding-you, TANG Bo. Optimizing model and algorithms of loading and packing multi-piece freights into one car [J]. Journal of the China Railway Society, 2011, 33: 1–9. (in Chinese)

[23] TENG H F, CHEN Y. A dual-system variable-grain cooperative coevolutionary algorithm: satellite-module layout design [J]. IEEE Transactions on Evolutionary Computation, 2010, 14(3): 438–455.

[24] ZHU W B, LIM A. A new iterative-doubling greedy–lookahead algorithm for the single container loading problem [J]. European Journal of Operational Research, 2012, 222: 408–417.

[25] PARRENO F, ALVAREZ-VALDES R, OLIVEIRA J F. A maximal-space algorithm for the container loading problem [J]. Informs Journal on Computing, 2008, 20: 412–422.

[26] WEI L J, OON W C, ZHU W B, LIM A. A reference length approach for the 3D strip packing problem [J]. European Journal of Operational Research, 2012, 220: 37–47.

[27] ZHANG De-fu, PENG Yu, ZHU Wen-xing, CHEN H W. A hybrid simulated annealing algorithm for the three- dimensional packing problem [J]. Chinese Journal of Computers, 2009, 32(11): 2147–2156. (in Chinese)

(Edited by HE Yun-bin)

中文导读

一种带平衡约束的三维装载问题双层混合局域搜索算法

摘要：带平衡约束的三维装载问题是指将一批具有不同尺寸和密度的匀质矩形物品合理装载于一个矩形箱子，要求在满足装载重心平衡的条件下来实现箱子空间利用最大化目标，本文设计了一种双层混合局域搜索算法(BHLS)对问题求解。算法将框架式布置思想和核心块生成策略结合起来，通过组合块的构造及装载系列的优化，确定各物品单元的装填顺序和布局位置。设计的双层算法的外层搜索负责合理装载模式的搜索，内层搜索用来确定各模式中的核心块及其最佳布局位置。使用包含物品尺寸差异强弱不同的标准算例进行试验，结果表明算法对带平衡约束的算例可使平均装载率从79.85%提高到86.45%，对不考虑平衡约束的算例也达到89.44%的较高平均装载率。

关键词：三维装载；带平衡约束；框架布局法；双层混合局域搜索；核心块

Foundation item: Project(16B134) supported by Hunan Provincial Department of Education, China

Received date: 2016-07-21; Accepted date: 2017-05-10

Corresponding author: ZHU Xiang, PhD, Lecturer; Tel: +86–731–82826538; E-mail: cszhuxiang@163.com; ORCID: 0000-0002-7095- 1878