DOI: 10.11817/j.issn.1672-7207.2015.11.043
随机车流作用下悬索桥钢桥面板疲劳损伤与寿命评估
鲁乃唯1, 2，刘扬2，邓扬2
(1. 东南大学 土木工程学院，江苏 南京，210096；
2. 长沙理工大学 土木与建筑学院，湖南 长沙，410114)
摘要：为了评估大跨度悬索桥钢桥面板在车流荷载作用下疲劳安全性，在实测车流数据的基础上，采用有限元数值模拟方法对某主跨为820 m的悬索桥钢箱梁顶板-U型肋构造细的疲劳损伤及寿命进行研究。通过对动态称重(WIM)实测车流数据的统计分析建立随机车流模型，基于应力-寿命(S-N)曲线和线性累积损伤准则分析运营状态和交通量增长对悬索桥钢桥面板构造细节疲劳损伤及寿命的影响。研究结果表明：随着密集运行车辆占有率的增加，疲劳损伤呈较缓增长趋势；随着交通量系数的增长，疲劳损伤呈加速增长趋势。与密集运行车辆占有率相比，交通量增长系数对疲劳损伤有较大的影响。在交通量增长系数达到6%时，钢桥面板细节疲劳寿命小于设计基准期，基于实测车流数据的疲劳性能评估对确保钢桥面板在运营期的安全性尤为重要。
关键词：钢桥面板；累积损伤；疲劳寿命；随机车流
中图分类号：U441+.4；U448.25 文献标志码：A 文章编号：1672-7207(2015)11-4300-07
Fatigue damage and life assessment for steel decks of suspension bridge under stochastic traffic flow
LU Naiwei1, 2, LIU Yang2, DENG Yang2
(1. School of Civil Engineering, Southeast University, Nanjing 210096, China;
2. School of Civil Engineering and Architecture, Changsha University of Science and Technology,
Changsha 410114, China)
Abstract: In order to assess fatigue safety of steel decks of long-span suspension bridges, the fatigue damage and life for steel decks of a suspension bridge with 820 m mid-span were investigated based on finite element analysis (FEA) and test traffic data. The random traffic flow was established based on test data on the basis of weigh-in-motion (WIM) system. Parameters were analyzed for influence of vehicle operating states and increment of traffic on fatigue damage and life for steel deck details of the suspension bridge, based on stress-life (S-N) curves and linear cumulative rule. The results show that the fatigue damage increases slowly with the increase of occupancy of heavy traffic flow. The fatigue damage increases rapidly with the growth of traffic volume. Traffic increment has a considerable effect on structural fatigue damage than the occupancy of heavy traffic flow. When the traffic increment reaches 6%, fatigue life of steel deck details will be lower than the design life. Fatigue property assessment ultilizing actual traffic data are especially important for ensuring safety of steel decks during service life.
Key words: steel bridge deck; accumulated damage; fatigue life; random traffic flow
大跨度斜拉桥和悬索桥一般采用具有较好抗风性能的流线型扁平钢箱梁结构，其正交异性桥面板在车辆荷载的反复作用下低于极限拉伸强度时会出现疲劳裂纹的萌生和扩展，达到一定程度之后即会突然断裂。针对这一问题，国内外学者通过数值模拟和模型试验等方式对其疲劳破坏模式、疲劳损伤演化机理及疲劳可靠度等方面进行深入的研究[1-3]。钢结构疲劳分析的基础是获取疲劳应力谱，其方法有基于有限元的数值模拟方法和基于长期健康监测的状态评估方法。叶华文等[4]通过对重庆两江大桥正交异性桥面板细节的足尺模型试验和有限元模拟分析研究了面内和面外荷载对桥面板寿命损伤的影响。郭彤等[5]基于应力-寿命(S-N)曲线法和长期健康监测数据对润扬长江大桥钢箱梁的顶板-U型肋细节疲劳寿命进行了评估。Zhang等[6]基于数值模拟方法对考虑车速和路面平整度的既有钢板桥的疲劳可靠度进行了评估，认为车速和路面平整度对疲劳损伤有较大的影响。Guo等[7]通过健康监测系统(SHM)采用的车辆数据加载到随机有限元分析中，得出了数值模拟方法与基于SHM实测应力统计分析方法得出的损伤值相同的结论。上述研究为基于数值模拟的疲劳寿命评估提供了有利条件。基于SHM系统提取的应力数据可对结构疲劳性能做出准确的评估，由于经济原因，既有桥梁很少安装该系统。而基于数值模拟方法对该类桥梁的疲劳性能评估有更好的适用性。目前主要采用疲劳荷载谱加载的方式获取结构应力谱[8]，该方法无法真实反映实际交通荷载情况。基于交通量统计的随机车流方法能够考虑实际车辆荷载的统计特征[9]，如车型、车质量、车速、行车间距及日交通量等，可应用于桥梁结构应力谱的提取及疲劳性能评估中。本文作者拟在某悬索桥动态称重(WIM)系统的基础上建立随机车流模型，采用数值模拟方法获取稀疏和密集运营状态下悬索桥钢箱梁细节的疲劳应力循环，基于S-N曲线和线性累积损伤准则对考虑交通量增长的悬索桥钢箱梁构造细节疲劳损伤及疲劳寿命进行分析。
1 车流作用下钢箱梁细节疲劳损伤的数学模型
钢结构疲劳损伤的分析方法主要有基于S-N曲线和Palmgren-Miner线性累积损伤准则方法(S-N曲线法)和基于Paris裂纹扩展模型的线弹性断裂力学法(LEFM方法)[10]。其中，Palmgren-Miner线性累积损伤理论认为，结构的总疲劳损伤是由变幅应力循环所造成疲劳损伤的线性叠加：
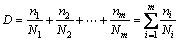(1)
式中：ni为应力循环数；Ni为S-N曲线中常幅应力幅值为Si的应力总循环数。随机车流作用下钢箱梁的应力循环幅值具有变幅和高频特征，不能直接应用式(2)所示的S-N曲线方程反映应力幅值和应力循环数的 关系。
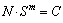(2)
式中：S为应力幅值；N为当应力幅值为S时对应的应力循环数；C为材料性能参数；m为S-N曲线图中lg N 和lg S曲线的反斜率。Eurocode 3(EC3)规范[11]通过疲劳细节和疲劳应力幅值的详细分类，给出了式(2)中的C和m。
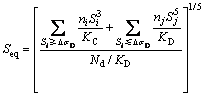
由于正交异性桥面板的应力循环中大部分应力均小于常幅疲劳极限△σD[12]，须将变幅应力循环采用根据疲劳损伤等价原则转换为等效应力循环后即可解决上述问题。EC3规范中顶板-U型肋(细节编号为50)的常幅疲劳极限△σD＝37 MPa。根据该规范将变幅应力循环等效为小于常幅疲劳极限△σD的等效常幅应力幅值Seq为：
(3)
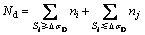(4)
式中：Si和ni分别为应力谱中大于常幅疲劳极限△σD的应力幅值和对应的循环数；Sj和nj分别为应力谱中小于△σD的应力幅值和对应的循环数；KC和KD分别为应力幅值大于和小于△σD的疲劳强度系数；Nd为日循环数。
为了考虑车辆的不同运行状态以及交通量增长对疲劳损伤的影响，根据车辆的行驶间距将桥梁的运营状态分为一般运营状态和密集运营状态。则考虑不同运营状态的结构损伤函数为
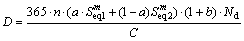(5)
式中：a为单日密集运行车辆占单日车辆的比例；b为交通量增长系数；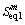
为密集运营状态下桥梁构造细节的等效应力幅值；
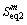为稀疏运营状态下桥梁构造细节的等效应力幅值。
根据上述疲劳损伤数学模型的建立过程，本文将车流作用下钢箱梁细节损伤及寿命评估分析流程划分为以下3个子步骤：基于有限元的应力时程分析、提取疲劳应力数据和疲劳寿命评估，如图1所示。
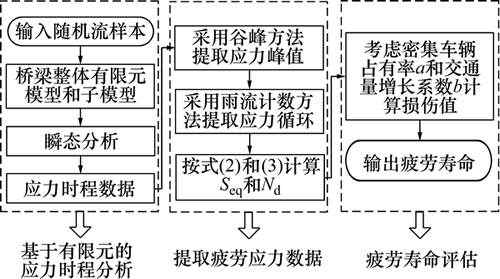
图1 车流作用下桥梁构造细节的疲劳寿命分析流程
Fig. 1 Flow chart for fatigue life analysis of bridge details under traffic flow
2 随机车流作用下悬索桥疲劳应力统计分析
2.1 工程背景
某单跨钢箱梁悬索桥主跨L=820 m，主缆横桥向中心间距为29.1 m，钢箱梁共65个，标准长度为12.8 m。
为了准确模拟车流荷载作用下钢箱梁正交异性桥面板-U型肋细部构造的受力特征，基于ANSYS软件建立了全桥整体模型和主梁局部子模型，如图3所示。整体模型中，索塔为Beam4梁单元，主梁为Shell63壳单元，主缆和吊杆为Link8杆单元。子模型为Shell63壳单元。车辆为Mass21质量单元，车辆与主梁通过Combin12弹簧单元连接。
2.2 随机车流模拟
基于WIM(动态称重)系统，取文献[13]中车型数据C1(小型客车)、C2(双轴货车)、C5(三轴货车)、C11(四轴挂车)、C14(五轴挂车)和C16(六轴挂车)为代表车型，其余车型按文献[13]采用的等效轴重原理转换为相近车型。在时域内生成随机车流的步骤如图4所示。
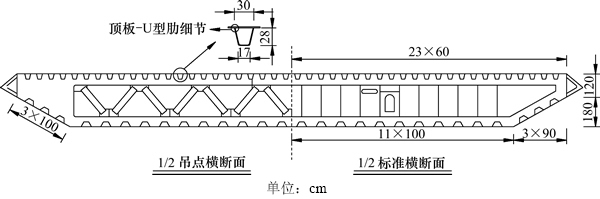
图2 钢箱梁横截面图
Fig. 2 Cross section of steel box girder
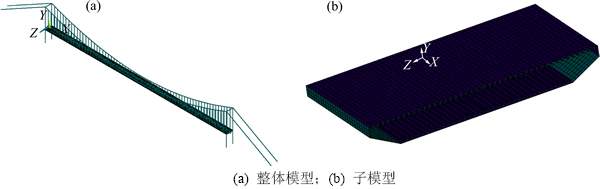
图3 有限元模型
Fig. 3 Finite element models
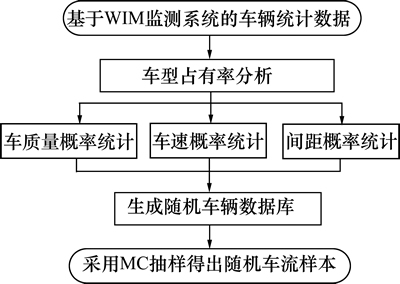
图4 随机车流模拟流程图
Fig. 4 Flow chart for simulation of random traffic flow
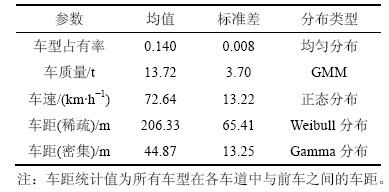
一般情况下，车型服从均匀分布，车速服从正态分布，由于车质量不能采用单一的高斯分布或极值-Ⅰ型分布描述，本文采用文献[14]提出的GMM(高斯混合模型)方法建立了各车型车质量的分布函数。文献[15]研究结果表明一般运营状态下车间距服从Weibull分布，而密集运营状态下行车间距服从Gamma分布。结合宜泸高速交通量特征与文献[15]的研究成果，本文将2辆车通过同一监测断面时间间隔为2 s以上的车辆划分为一般运行状态，相反则为密集运行状态。其中，C5车型的统计值如表1所示。
表1 C5车型的统计值
Table 1 Statistic of vehicle model of C5
在Matlab平台，采用Monte-Carlo抽样生成的一般运营状态与密集运营状态的随机车流样本如图5 所示。
2.3 疲劳应力统计分析
宋永生等[16]对润扬长江大桥正交异性桥面板构的两类焊接细节应力分析表明：顶板-U形肋交界点的应力幅值与循环数均较纵肋对接处的大。因此，本文选取主梁L/4和L/2处的顶板-U形肋交界点进行应力时程分析。
暂取车流通行时间为5 min，荷载子步积分时间为0.16 s。密集运营状态下共通过的车辆数为400辆，一般运营状态下共通过的车辆数为160辆。按照图1所示的“基于有限元的应力时程分析”步骤求解结构的动力响应。稀疏运营状态和密集运营状态下主梁L/4和L/2的顶板-U肋处应力时程如图6所示。
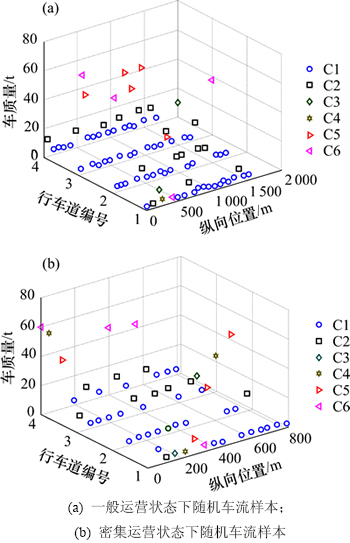
图5 随机车流样本图
Fig. 5 Random samples of random traffic flow
由图6可知：在5 min内的随机车流作用下，悬索桥钢箱梁细节应力范围为±40 MPa，且一般均小于20 MPa，具有低应力幅值和高频率特点。跨中响应值较L/4处的大，密集运营状态下响应值较一般运营状态下的大。
为了进一步分析不同运营状态下钢箱梁细节疲劳应力幅值与循环数的变化，按流程图1所示“提取疲劳应力数据”步骤，将密集运营状态下的应力时通过谷峰方法和雨流计数法进行提取。其中主梁跨中的应力循环如图7所示。
在提取应力循环之后，由式(3)和(4)计算等效应力幅值Seq和循环数Nd。针对本工程背景中钢箱梁顶板-U型肋的构造细节，按EC3规范中的细节类型为50，其常幅应力极限△σD=37 MPa，应力截止限为△σL=20 MPa，KC和KD分别为2.50×1011和3.47×1014。本文将所有应力循环均计入疲劳损伤中，不对△σL进行筛选，这样得到的疲劳损伤更精确。在5 min内的不同运营状态及不同截面位置处的损伤值与等效应力幅值如表2所示。
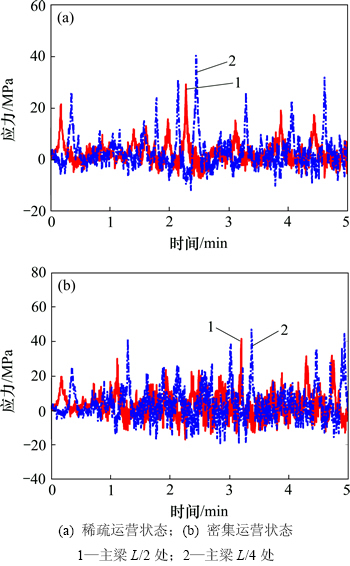
图6 5 min内主梁构造细节的应力响应时程图
Fig. 6 Displacement response time history diagram of girder nodes and power spectral density in 5 min
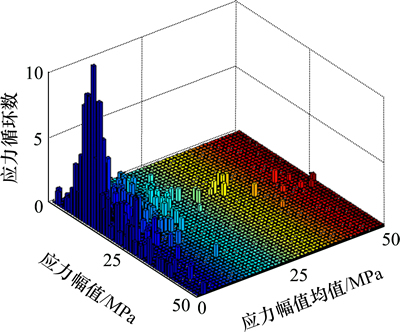
图7 经谷峰方法和雨流计数法提取的应力循环
Fig. 7 Extracted stress cycles using Gu-feng method and rain flow counting method
表2 5 min内钢箱梁顶板-U型肋处的疲劳损伤
Table 2 Damage values of rib-to-deck connections of steel box girders in 5 min
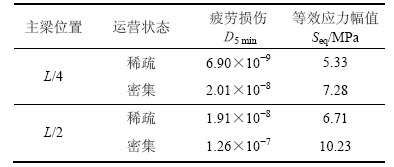
由表2可知：在相同的运营状态下，跨中主梁的日损伤值与等效应力幅值均较L/4处的大，其中等效应力幅值约为L/4处的1.26倍。密集运营状态下主梁跨中的等效应力幅值Seq是稀疏运营状态下的1.52倍。
3 钢箱梁细节疲劳寿命评估
在得到随机车流作用下钢箱梁细节应力幅值与循环数统计特征后，由式(5)计算考虑密集运行车辆占有率a及交通量增长系数b的疲劳损伤。
首先分析密集运行车辆占有率a对疲劳损伤的影响。暂取式(5)中，交通量线性增长系数b=0，密集运行车辆占有率为a=[0, 1%, 2%, 3%, 4%, 5%, 6%]。密集运行车辆对疲劳损伤的影响如图8所示。
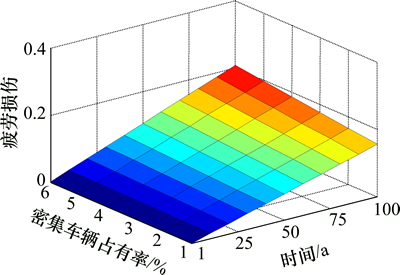
图8 密集运行车辆对疲劳损伤的影响
Fig. 8 Influence of heavy traffic occupancy on fatigue damage
由图8可知：当密集运行车辆占率由1%增加到6%后，100 a后钢箱梁细节疲劳损伤由0.16增加到0.21。密集运行车辆增长5%导致疲劳损伤增加0.3倍。当密集车辆占有率a＝6%时，1~100 a的疲劳损伤由0.002 1增加到0.210 0。这说明，随着运营时间的增加，钢箱梁细节累积疲劳损伤呈线性增长趋势，而密集运行车辆占有率的增长使疲劳损伤增加较缓。
实际交通量会随社会发展水平的提高而增长，因此钢箱梁细节处的循环数会增加，因此，应分析交通量增长对疲劳损伤的影响。暂取密集运行车辆占有率a=6%，交通量线性增长系数b=[1%, 2%, 3%, 4%, 5%, 6%]。交通量增长对疲劳损伤的影响如图9所示。
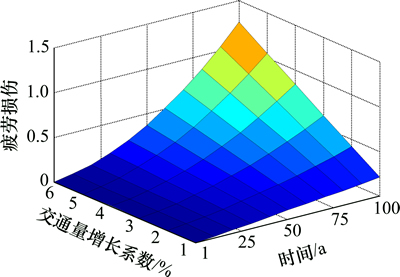
图9 交通量增长系数对疲劳损伤的影响
Fig. 9 Influence of traffic increment on fatigue damage
由图9可知：100 a后，当交通量增长系数由1%增加至6%后，在第1年运营期内，钢箱梁细节累积疲劳损伤由0.002 1增加至0.002 2。在100 a后，疲劳损伤由0.23增加至1.26。由此可知：交通量增长5%导致疲劳损伤增加4.5倍。随着运营期的增加，荷载增长系数对疲劳损伤呈加速增加趋势。
分别研究了密集运行车辆占有率a和交通量增长系数b在1~100 a内对疲劳损伤的影响。为了对比a和b同时对疲劳损伤及疲劳寿命的影响，在100 a的运营期内，钢箱梁细节疲劳损伤如图10所示。
由图10可知：与密集运行车辆占有率相比，交通量增长系数对疲劳损伤更大的影响，且当交通量增长系数达到6%时，100 a后的疲劳损伤已经超过1。当疲劳损伤达到临界损伤D=1时，对应的疲劳寿命如图11所示。
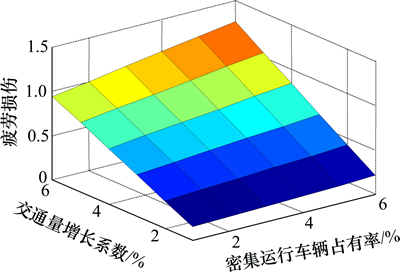
图10 a和b同时对疲劳损伤的影响
Fig. 10 Influence of combined effect of a and b on fatigue damage
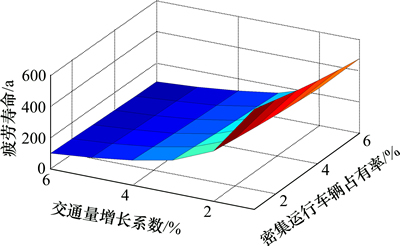
图11 a和b同时对疲劳寿命的影响
Fig. 11 Influence of combined effect of a and b on fatigue life
由图11可知：在交通量确定的情况下，随着密集运营行车辆的占有率的增加，顶板-U型肋细节疲劳寿命呈缓慢降低趋势。在密集运行车辆占有率确定的情况下，随着交通量的增长其疲劳寿命呈加速降低趋势。在交通量增长系数达到6%时，钢箱梁细节疲劳寿命小于设计基准期。这表明了桥梁的交通量统计对其疲劳寿命评估尤为重要。
4 结论
1) 在相同的运营状态下，跨中主梁的日损伤值与等效应力幅值均较L/4处的大，其中等效应力幅值约为L/4处的1.26倍。密集运营状态下的等效应力幅值Seq是稀疏运营状态下的1.52倍。
2) 密集运行车辆占有率增长5%将导致疲劳损伤增加0.3倍。随着密集运行车辆占有率的增加，疲劳损伤呈较缓增长趋势，疲劳寿命呈缓慢降低趋势。
3) 交通量增长5%将导致疲劳损伤增加4.5倍。随着交通量系数的增长，疲劳损伤呈加速增长趋势，疲劳寿命呈加速降低趋势。与密集运行车辆占有率相比，交通量增长系数对疲劳损伤及寿命有更大的影响。
4) 在交通量增长系数达到6%时，钢箱梁细节疲劳寿命小于设计基准期。基于实测车流数据的疲劳性能评估对确保钢桥面板在运营期的安全性尤为重要。
5) 本文在随机车流模拟中未考虑路面平整度，风荷载和构造细节的初始缺陷对疲劳寿命具有一定的影响，今后也可从疲劳的微观机理方面对疲劳裂纹的形成和扩展进行研究。
参考文献：
[1] Chen Z W, Xu Y L, Xia Y, et al. Fatigue analysis of long-span suspension bridges under multiple loading: Case study[J]. Engineering Structures, 2011, 33(12): 3246-3256.
[2] 王春生, 付炳宁, 张芹, 等. 正交异性钢桥面板足尺疲劳试验[J]. 中国公路学报, 2013, 26(2): 69-76.
WANG Cunsheng, FU Bingyu, ZHANG Qin, et al. Fatigue test on full-scale orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2013, 26(2): 69-76.
[3] GUO Tong, CHEN Yuwen. Field stress/displacement monitoring and fatigue reliability assessment of retrofitted steel bridge details[J]. Engineering Failure Analysis, 2011, 18(1): 354-363.
[4] 叶华文, 徐勋, 强士中, 等. 重庆两江大桥正交异性钢桥面板疲劳性能试验研究[J]. 中南大学学报(自然科学版), 2013, 44(2): 749-756.
YE Huawen, XU Xun, QIANG Shizhong, et al. Fatigue test of orthotropic steel bridge deck in Chongqing Liangjiang Bridge[J]. Journal of Central South University (Science and Technology), 2013, 44(2): 749-756.
[5] 郭彤, 李爱群. 基于长期监测数据的桥面板焊接细节疲劳寿命评估[J]. 土木工程学报, 2009, 42(6): 66-72.
GUO Tong, LI Aiqun. Fatigue life assessment of welds in bridge decks using long term monitored data[J]. China Civil Engineering Journal, 2009, 42(6): 66-72.
[6] ZHANG Wei, Cai C S. Fatigue reliability assessment for existing bridges considering vehicle speed and road surface conditions[J]. Journal of Bridge Engineering, 2012, 17(3): 443-453.
[7] Guo T, Frangopol D M, Chen Y. Fatigue reliability assessment of steel bridge details integrating weigh-in-motion data and probabilistic finite element analysis[J]. Computers & Structures, 2012, 112: 245-257.
[8] 周泳涛, 鲍卫刚, 翟辉, 等. 公路钢桥疲劳设计荷载标准研究[J]. 土木工程学报, 2010, 43(11): 79-85.
ZHOU Yongtao, BAO Weigang, ZAI Jun, et al. Study on standard fatigue design load for steel highway bridges[J]. China Civil Engineering Journal, 2010, 43(11): 79-85.
[9] Chotickai P, Bowman M D. Truck models for improved fatigue life predictions of steel bridges[J]. Journal of Bridge Engineering, 2006, 11(1): 71-80.
[10] HE Jingjing, LU Zizi, LIU Yongming. New method for concurrent dynamic analysis and fatigue damage prognosis of bridges[J]. Journal of Bridge Engineering, 2012, 17(3): 396-408.
[11] Eurocode3—2005. Design of steel structures. Part 1-9: Fatigue[S].
[12] 王春生, 冯亚成. 正交异性钢桥面板的疲劳研究综述[J]. 钢结构, 2009, 24(9): 10-13.
WANG Cunsheng, FENG Yacheng. Review of fatigue research for orthotropic steel bridge decks[J]. Steel Structures, 2009, 24(9): 10-13.
[13] 王达. 基于有限元模型修正的大跨度悬索桥随机车流车-桥耦合振动分析[D]. 西安: 长安大学公路学院, 2008: 12-19.
WANG Da. Analysis of vehicle-bridge coupled vibration for long-span suspension bridge with finite element model updating under random traffic flowing[D]. Xi’an: Chang’an University. College of Highway, 2008: 12-19.
[14] Calcada R, Cunha A, Delgado R. Analysis of traffic-induced vibrations in a cable-stayed bridge. Part II: Numerical modeling and stochastic simulation[J]. Journal of Bridge Engineering, 2005, 10(4): 386-397.
[15] 宗周红, 李峰峰, 夏叶飞, 等. 基于 WIM 的新沂河大桥车辆荷载模型研究[J]. 桥梁建设, 2013, 43(5): 29-36.
ZHONG Zhouhong, LI fengfeng, XIA Yefei, et al. Study of vehicle load models for Xinyi river bridge based on WIM data [J]. Bridge Construction, 2013, 43(5): 29-36.
[16] 宋永生, 丁幼亮, 王晓晶, 等. 运营状态下悬索桥钢桥面板疲劳效应监测与分析[J]. 工程力学, 2013, 30(11): 94-100.
SONG Yongsheng, DING Youliang, WANG Xiaojing, et al. Monitoring and analysis of fatigue effects on steel deck of a suspension bridge under actual conditions[J]. Engineering Mechanics, 2013, 30(11): 94-100.
(编辑 杨幼平)
收稿日期：2014-11-02；修回日期：2015-02-28
基金项目(Foundation item)：国家重点基础研究发展规划(973计划)项目(2015CB057705)；国家自然科学基金资助项目(51378071, 51308073)；湖南省自然科学基金资助项目(14JJ3087) (Project(2015CB057705) supported by the National Basic Research Development Program (973 Program) of China; Projects(51378081, 51308073) supported by the National Natural Science Foundation of China; Project (14JJ3087) supported by the Natural Science Foundation of Hunan Province)
通信作者：鲁乃唯，博士(后)，从事桥梁结构可靠度评估与安全控制研究；E-mail: lunaiweide@163.com
