混凝土薄壁连续箱梁剪力滞效应试验研究

祝明桥^{1, 2}

(1. 中南大学 土木工程博士后流动站，湖南 长沙，410075；

2. 湖南科技大学 土木工程学院，湖南 湘潭，411201)

摘  要：对大比例长悬臂梯形截面混凝土薄壁连续箱梁在弹性范围内的剪力滞效应进行试验研究与分析，并研究在各级荷载作用下，中间支座和跨中截面荷载-挠度曲线以及翼缘混凝土应变分布规律等。考虑翼缘弯曲正应力沿宽度方向和厚度方向的不均匀性，给出翼缘等效宽度计算系数公式；根据试验结果，得到连续箱梁中间支座和跨中截面翼缘等效宽度计算系数，并和现行JTG D62—2004规范中翼缘等效宽度计算系数计算结果进行比较。研究结果表明：混凝土薄壁连续箱梁无论在中间支座处，还是在跨中截面均存在正剪力滞现象；规范连续箱梁翼缘等效计算系数公式偏于安全。

关键词：桥梁工程；连续箱梁；剪力滞效应；混凝土；翼缘有效宽度计算系数

中图分类号：U488.219         文献标识码：A         文章编号：1672-7207(2008)02-0375-05

Experimental research and analysis on shear lag effect ofconcrete thin-walled box continuous girder

ZHU Ming-qiao^{1, 2}

(1. Post-Doctor Work Station of Civil Engineering, Central South University, Changsha 410075, China;

2. School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)

Abstract: A test on the shear lag effect of the long flanges and thin-walled box continuous girder of trapezoidal section high-strength concrete was studied in elastic stage. The deflection at mid-span and concrete strain distribution of the flanges in mid-supported and mid-span sections were studied. Considering the flexural stress distribution inhomogeneity along width and thickness of flanges, the formula on equivalent calculated coefficient of flange width was proposed. The experimental values of equivalent calculated coefficient of flange width in mid-supported and mid-span sections were given. The results show that the shear lag phenomena are confirmed in mid-supported and mid-span sections. Compared with the values in the code JTG D62—2004, the calculated values are safer.

Key words: bridge engineering; continuous box girder; shear lag effect; concrete; equivalent calculated coefficient of effective flange width

混凝土薄壁箱梁截面抗弯刚度大，弯曲应力图形合理，能有效地抵抗正负弯矩，在施工和使用过程中具有较强的稳定性，能较好地适应各种现代施工方法(如悬臂施工、顶推施工等)要求，因此，在现代各种桥梁中得到广泛应用，且常被用作抗弯构件^[1-6]。但与传统的矩形截面混凝土受弯构件相比，混凝土薄壁箱梁截面抗弯应力沿翼缘板宽度范围的分布不均匀，存在剪力滞现象^[7-11]，因此，在应用初等混凝土梁理论解决混凝土薄壁箱梁正截面抗弯承载力计算时，需确定混凝土薄壁箱梁翼缘有效宽度。

近几十年来，大部分研究者是从解析理论和数值解法来研究有关混凝土薄壁箱梁剪力滞效应问题，而通过模型试验特别是大比例模型试验来研究混凝土薄壁箱梁剪力滞效应问题还很少^[12-14]。为此，本文作者通过大比例混凝土薄壁连续箱梁模型在弹性范围内抗弯性能试验研究，探讨混凝土薄壁连续箱梁支座和跨中截面剪力滞效应和翼缘等效分布宽度系数的变化规律，以期为在弹性范围内解决混凝土薄壁连续箱梁抗弯正截面抗弯承载力计算提供理论依据。

1  试  验

1.1  试件设计及材料力学性能

混凝土薄壁箱形桥梁多采用宽顶板、窄底板、长悬臂、斜腹板的梯形截面混凝土薄壁箱梁^[2-6]，本次试验模型也采用此类截面。模型长为6.0 m，两端各设有0.2 m厚横隔板，混凝土强度等级为C60，钢筋为HRB335级钢筋，箱梁模型设计尺寸如图1所示，混凝土和钢筋的力学性能见表1。

1.2  试验装置及仪表布置

混凝土薄壁连续箱梁采用二级分配梁对称4点集中力千斤顶加载，外荷载P由压力传感器和电子称读数控制；由于连续梁属于超静定结构，考虑连续梁在试验过程很难保证支座的绝对刚性，各支座的沉降可能不均匀引起构件内力的变化，故在试验过程中，在连续梁中间支座处放置压力传感器，以测得中间支座的反力，利用对称性，根据实际施加的外荷载P，通过计算得到2边支座的反力(R₁=R₂)。

为了全面研究混凝土连续箱梁模型剪力滞现象，利用模型的对称性，设有A-A，B-B和C-C共3个控制截面作为研究对象，如图1所示。每个控制截面顶板均布有9片混凝土应变片，其中B-B和C-C 2个控制截面底板布有5片混凝土应变片。为了较全面测得构件的整体变形，沿构件纵向在支座和跨中截面双向对称布置10个百分表。

(a) 模型平面图；(b) 截面尺寸及配筋

图1  模型箱梁截面尺寸及配筋(单位：mm)

Fig.1  Profile and reinforcements of cross section (Unit: mm)

2  试验结果与分析

在弹性范围内，混凝土薄壁连续箱梁模型的抗弯性能试验加载方法严格按照《混凝土结构试验方法标准》^[15]执行。考虑到混凝土受力基本处于弹性范围内，采用相同试验进行多次，同时利用截面的对称性，取其平均值作为最终的试验结果，主要研究成果包括：荷载-挠度曲线；在不同荷载作用下，混凝土薄壁连续箱梁中间支座、跨中截面顶板和底板应变分布等。

2.1  荷载-挠度曲线

混凝土薄壁连续箱梁在各级集中荷载作用下，测得构件跨中截面的荷载-挠度曲线如图2所示。

表1  钢筋及混凝土力学指标

                         Table 1  Properties of reinforcements and concrete                       MPa

图2  跨中截面荷载-挠度曲线

Fig.2  Curve of load-deflection at mid-span

从图2可以看出：连续梁在集中荷载作用处的挠度与荷载基本呈正比，说明连续梁大致处于线弹性工作状态。

2.2  不同截面处混凝土应变分布

混凝土薄壁连续箱梁在不同荷载作用下，实测的不同截面混凝土应变分布如图3所示。其中：取拉应变为正，压应变为负；距离是指离对称轴的距离。为了减小测试误差的影响，利用截面的对称性，将图中应变取为对称位置的应变平均值。

由于截面A-A截面处于两跨连续梁的中间支座处，在对称集中荷载作用下，截面承受负弯矩；同时，由于底板有支座支撑构件，存在局部作用影响，实际上仅取截面A-A顶板应变分布为主要研究对象，在各级荷载作用下，测得截面A-A顶板应变分布如图3(a)所示。从图3(a)可以看出：截面A-A顶板拉应变分布在腹板与顶板相交处最大，愈往两边应变愈小，呈现明显正剪力滞现象。

考虑连续梁在集中荷载作用的局部影响，取离集中荷载有一定距离(各250 mm处)的B-B和C-C两截面作为正弯矩作用时的研究对象，其中截面C-C为跨中截面。在各级荷载作用下，测得B-B和C-C两截面顶、底板应变分布如图3(b)~(e)所示。可以看出：尽管截面B-B与截面C-C承受的弯矩不同，但顶底板的应变分布规律有相似之处，即顶板受压，在腹板与顶板相交处压应变最大，愈往两边应变愈小，呈现明显正剪力滞现象；底板受拉，在腹板与底板相交处拉应变最大，愈往中间应变愈小，也呈现明显正剪力滞   现象。

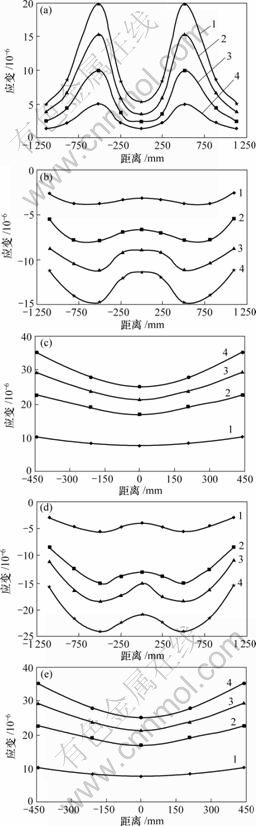
(a) A-A截面顶板应变分布；(b) B-B截面顶板应变分布；(c) B-B截面底板应变分布；(d) C-C截面顶板应变分布；(e) C-C截面底板应变分布

P/kN: 1—35.7; 2—79.7; 3—96.2; 4—118.2

图3  不同截面处混凝土应变分布

Fig.3  Concrete strain distribution in different sections

3  翼缘等效宽度分析

3.1  翼缘等效宽度计算系数定义

混凝土薄壁箱梁翼缘有效宽度，一般采用翼缘等效宽度计算系数来描述。我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)^[16](以下简称JTG D 62—2004规范)中有关箱形截面翼缘等效宽度计算系数的定义，是以与肋板相交处翼板表面的正应力为标准时的翼板折算宽度与实际翼板宽度   之比。

由于混凝土薄壁箱梁存在剪力滞现象，使得翼板内弯曲正应力沿梁宽方向分布不均匀；同时，翼板内弯曲正应力沿厚度方向分布也存在不均匀性，如图4所示。因此，混凝土薄壁箱梁截面翼缘等效宽度计算系数应考虑箱形截面翼缘内应力沿宽度和厚度方向分布的不均匀性，其严格的数学表达式为：

图4  混凝土薄壁箱梁分析模型

Fig.4  Analysis model of concrete thin-walled box

3.2  翼缘等效宽度计算系数对比分析

根据混凝土薄壁连续箱梁在不同荷载作用下，实测的不同截面混凝土应变分布，代入相应的翼缘等效宽度系数计算公式，得到不同截面翼缘等效宽度计算系数；同时，按JTG D62—2004规范计算公式，代入相关试件参数，得到支座负弯矩截面处的上外、上内翼缘等效计算系数和跨中正弯矩截面处的上外、上内和下内翼缘等效计算系数，如表2所示。

表2  翼缘等效宽度计算系数

Table 2  Equivalent calculated coefficients of flange width

通过对比可以看出：混凝土薄壁连续箱梁在支座负弯矩截面处的上外、上内翼缘等效计算系数，规范计算结果与试验分析结果之比分析为72.2%和66.9%；在跨中正弯矩截面处的上外、上内和下内翼缘等效计算系数，规范计算结果与试验分析结果之比分析为67.4%~70.6%，80.9%~83.9%和88.9%~94.5%。

4  结  论

a. 负弯矩区(中间支座处)和正弯矩区(跨中截面附近)均存在正剪力滞现象，但剪力滞效应相差较大。

b. 在正弯矩区(跨中截面附近)，无论是受压翼缘(顶板)，还是受拉翼缘(底板)，均存在正剪力滞现象，且剪力滞效应相差不大。

c. 考虑翼缘弯曲正应力沿宽度方向和厚度方向的不均匀性，给出了翼缘等效宽度计算系数公式。

d. 根据试验结果，得到了连续箱梁中间支座和跨中截面翼缘等效宽度计算系数，并和现行JTG D62—2004规范中翼缘等效宽度计算系数计算结果比较，得出JTG D62—2004规范连续箱梁翼缘等效计算系数公式偏于安全。

参考文献：

[1] 郭金琼. 箱形梁设计理论[M]. 北京: 人民交通出版社, 1991.
GUO Jin-qiong. Theory and design of the box girder[M]. Beijing: China Communications Press, 1991.

[2] 项海帆. 高等桥梁结构理论[M]. 北京: 人民交通出版社, 2001.
XIANG Hai-fan. Theory of the highway bridge structures[M]. Beijing: China Communications Press, 2001.

[3] 张士铎, 邓小华, 王文州. 箱形薄壁梁剪力滞效应[M]. 北京: 人民交通出版社, 1998.
ZHANG Shi-duo, DUN Xiao-hua, WANG Wen-zhou. Shear lag effect on the thin-walled box girder[M]. Beijing: China Communications Press, 1998.

[4] 周凌宇, 康习军, 余志武, 等. 钢-混凝土组合梁的非线性杆系有限元分析[J]. 中南大学学报: 自然科学版, 2004, 35(2): 316-321.
ZHOU Ling-yu, KANG Xi-jun, YU Zhi-wu, et al. The finite element analysis for composite beams of steel and concrete[J]. Journal of Central South University: Science and Technology, 2004, 35(2): 316-321.

[5] GB 50010—2002, 混凝土结构设计规范[S].
GB 50010—2002, Code for design of concrete structures[S].

[6] Song O G, Alexander C. Shear-lag analysis of T, I, and box beams[J]. Journal of Engineering Mechanics, 1994, 116(5): 1290-1304.

[7] Alghamdi S A. Static and modal analysis of thin-walled box girder structures[J]. AIAA Journal, 2001, 39(7): 1406-1410.

[8] 郭金琼, 房贞政, 罗孝登. 箱形梁桥剪力滞效应分析[J]. 土木工程学报, 1983, 16(1): 1-13.
GUO Jin-qiong, FANG Zhen-zheng, LUO Xiao-dun. Analysis of shear lag effect on the box girder[J]. China Civil Engineering Journal, 1983, 16(1): 1-13.

[9] 祝明桥. 混凝土薄壁箱梁受力性能的试验研究与分析[D].长沙: 湖南大学土木工程学院, 2005.
ZHU Ming-qiao. Experimental research and analysis on the behavior of concrete thin-walled box girder[D]. Changsha: School of Civil Engineering, Hunan University, 2005.

[10] 祝明桥. 悬臂混凝土薄壁箱梁剪力滞效应试验研究与分析[J]. 湘潭大学学报: 自然科学版, 2007, 29(3): 103-107.
ZHU Ming-qiao. Experimental research and analysis on the shear lag effect of high-strength concrete thin-walled box continuous girder[J]. Journal of Xiangtan University: Natural Science, 2007, 29(3): 103-107.

[11] 祝明桥, 冷辉平. 混凝土薄壁箱梁变形与裂缝试验研究与分析[J]. 湖南科技大学学报: 自然科学版, 2007, 22(4): 23-26.
ZHU Ming-qiao, LENG Hui-ping. Experimental research and analysis on the crack and deformation of concrete thin-walled box girder[J]. Journal of Hunan University of Science and Technology: Natural Science, 2007, 22(4): 23-26.

[12] 罗旗帜, 吴幼明. 薄壁箱梁剪力滞理论的评述和展望[J]. 佛山科学技术学院学报, 2001, 19(3): 29-35.
LUO Qi-zhi, WU You-ming. Comments and prospect on the theories of the shear lag in thin-walled box girders[J]. Journal of Foshan University: Natural Science Edition, 2001, 19(3): 29-35.

[13] Garden H N, Hollaway L C. An experimental study of the failure modes of reinforced concrete beams strengthened with prestressed carbon composites plates[J]. Composites: Part B, 1998, 29: 411-424.

[14] Wight R G, Green M F, Erki M A. Prestressed FRP sheets for post strengthening reinforced concrete beams[J]. ASCE Journal of Composites for Construction, 2004, 5(4): 214-220.

[15] GB50152—92, 混凝土结构试验方法标准[S].
GB50152—92, Standard methods for testing of concrete structures[S].

[16] JTG D62—2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
JTG D62—2004, Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].