基于神经网络辨识的移动机器人航向误差校准方法

于金霞^{1, 2}, 蔡自兴¹, 邹小兵¹, 段琢华^{1, 3}

(1. 中南大学 信息科学与工程学院, 湖南 长沙, 410083;

2. 河南理工大学 计算机科学与技术学院, 河南 焦作, 454003;

3. 韶关学院 计算机科学系, 广东 韶关, 512003)

摘要: 分析了E-Core RD1100干涉型光纤陀螺的误差产生机理, 提出利用RBF神经网络和遗传算法实现光纤陀螺漂移误差模型的辨识。 通过实验获得进化神经网络的训练样本, 在RBF神经网络的训练中, 提出了基于Elitist竞争机制的遗传进化训练方法。 RBF神经网络具有很强的局部逼近能力, 而遗传算法具有优良的全局搜索与优化性能, 从而能够有效地对陀螺误差的非线性与时变特征进行建模与辨识。 实验结果表明: 该方法大幅度减少了光纤陀螺的误差, 从而提高了移动机器人导航定位的精度。

关键词: 移动机器人; 光纤陀螺; 径向基函数神经网络; 遗传算法; 最优竞争机制

中图分类号:TP24 文献标识码:A 文章编号: 1672-7207(2005)05-0745-06

Calibration method for heading error of mobile robot based on neural networks identification

YU Jin-xia^{1, 2}, CAI Zi-xing¹, ZOU Xiao-bing¹, DUAN Zhuo-hua^{1, 3}

(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;

2. Institute of Computer Science and Technology, Henan Polytechnic University, Jiaozuo 454003, China;

3. Department of Computer Science, Shaoguan University, Shaoguan 512003, China)

Abstract: The basis of error occurrence of E-Core RD1100 interferometric fiber optic gyros (FOG) was analysed. Radial basis function neural network (RBFNN) and genetic algorithm (GA) were adopted to realize the identification of error model for FOG. The training samples were obtained by experiments and the genetic evolutionary method based on elitist rule was presented for neural network training. RBFNN has a good capacity of local approximation, while GA is efficient in global optimization. So this method can be used to realize the nonlinear and time-varying error modeling and identification. The experimental results show that it can reduce the error of FOG to a great extent and enhance the localization precision of mobile robot navigation.

Key words: mobile robot; fiber optic gyros; radial basis function neural network; genetic algorithm; elitist rule

   在移动机器人定位方法中, 航迹推算已经成为未知环境中移动机器人导航定位的主要方法^[1]。 陀螺作为航迹推算的关键部件, 用于测量移动机器人的航向角, 它的性能在很大程度上直接影响着移动机器人航向的精度^{[2, 3]}。 近年来, 光纤陀螺(FOG)以其潜在的优势和应用前景而备受重视, 广泛应用于移动机器人导航控制系统中^{[4, 5]}。

但是, 光纤陀螺存在累积漂移误差, 其受环境的影响很大, 误差模型具有时变性^{[5, 6]}。 因此, 对于光纤陀螺的漂移给移动机器人造成的航向误差需要精确辨识并进行有效校正。 本文作者在光纤陀螺漂移误差分析及常规校正研究基础上, 提出利用RBF神经网络和遗传算法所构建的进化神经网络实现光纤陀螺漂移误差模型的辨识, 并用它对移动机器人航向误差进行校正。 RBF神经网具有很强的局部逼近能力^{[7, 8]}, 而遗传算法具有优良的全局搜索与优化性能^{[9, 10]}, 从而能够有效地对陀螺的误差进行建模与辨识。 在RBF神经网络的训练中, 提出基于Elitist竞争机制的进化训练方法, 具有较快的收敛效率。 通过实验, 证明该方法可以大幅度减少光纤陀螺的误差, 从而提高移动机器人导航定位的精度。

1 航向误差分析及常规校正

1.1 误差分析

光纤陀螺漂移的产生原因比较复杂, 按误差性质可以分为随机漂移和零漂; 按产生原因可以分为由外部因素(如温度变化、 地球自转)和内部因素(如元器件的参数漂移、 工作特性)分别产生的误差; 按性能参数来分包括零漂、 标度因数非线性度、 角度随机游走、 量化噪声等。 造成光纤陀螺漂移误差复杂的原因是各种误差相互关联和相互影响。 实验中采用的E-Core RD1100数字输出速度陀螺是单轴采用干涉测量的光纤速度传感器^[11]。 图1所示为未经任何校正的静态E-Core RD1100光纤陀螺输出的原始数据曲线, 从图1可以看出角速率变化不是很明显, 而角度却在50 min内漂移了150°, 这无疑给移动机器人的定位和导航带来了困难。 通过理论分析和实验, 发现光纤陀螺对移动机器人航向所带来的误差影响因素主要为:

a. 零漂;

b. 标度因数的非线性度;

c. 环境温度所造成系统的时变特性。

1.2 常规校正

1.2.1 零漂

零漂即当输入旋转角速率为零时, 陀螺输出量围绕其均值的离散程度。 零漂是陀螺的固有误差, 可以通过软件设计解决。 一种常用的补偿过程是在陀螺处于静止没有做任何工作之前收集一些静止陀螺输出的漂移数据(比如10~20 s), 算出它们的平均值作为零漂, 进行后面的测量时从读数中减去该偏移值。

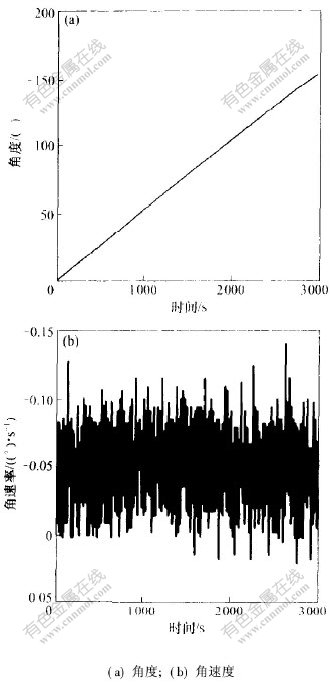
图 1   未经校正的FOG角度和角速率输出曲线(温度: 28.20~34.40 ℃)

Fig. 1   Output of angle and angular rate of FOG without any calibration

1.2.2 标度因数非线性度

标度因数非线性度(或称刻度因子误差)是指在输入角速率范围内, 陀螺仪输出量相对于最小二乘法拟合直线的最大偏差值和最大输出量之比。 通过KVH公司提供的E-Core RD1100光纤陀螺的性能参数分析, 以及对其在电控转台输入角速度为-25~+25 (°)/s之间的标度因数非线性度进行测试。 结果表明, 电控转台输入角速度为-25~+25 (°)/s时, RD1100光纤陀螺的标度因数非线性度非常小。 这说明标度因数非线性度对于研制的移动机器人的航向影响不大。

1.2.3 其他影响因素

通过研究发现, 由于光纤陀螺的数据采样周期为0.1 s, 系统程序中数据通讯过程需要0.1 s, 这样移动机器人当前获得的光纤陀螺数据实际上是0.2 s前的航向角度。 也就是说, 移动机器人系统存在0.2 s的时滞。 为了解决这一问题, 采用了动态系统的α-β滤波的状态预测方程对移动系统机器人系统进行状态补偿。 其基本思想参见文献[12]。

通过以上分析及常规校正, 在环境温度比较稳定的情况下, 将光纤陀螺的角度漂移控制在15~26 (°)/h。 但是, 由于光纤陀螺使用的实时性和对环境温度变化的灵敏性, 使得移动机器人利用光纤陀螺进行航迹推算时仍然不可避免地存在航向误差。

2 神经网络辨识方法

神经网络的类型很多, 鉴于RBF神经网络具有比目前应用较广泛的BP神经网络更强的逼近能力和更快的收敛速度, 这里选用RBF神经网络来实现光纤陀螺漂移误差的非线性辨识。 不过RBF神经网络隐含层的神经元个数及待估计参数较多, 传统的学习算法难以直接对这些众多参数进行有效地估计。 由于GA对于非线性问题求解和大范围空间搜索有其独特的优势, 这里选用GA来确定网络的结构和参数。

2.1 RBF神经网络模型

RBF神经网络与多层前馈神经网络类似, 由输入层、 隐含层和输出层3层组成。 具有n个输入和一个输出的RBF神经网络如图2所示, 设其输入为n维矢量X:

X=[x₁,x₂,…,x_n]^T。

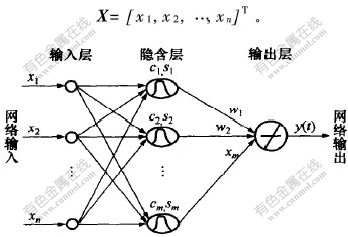
图 2   RBF神经网络的结构图

Fig. 2   Structure of RBFNN

选用高斯函数作为径向基函数, 则第j个隐节点对于输入矢量X的径向基函数为

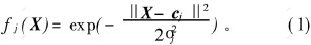
其中: c_j=(c_j1, c_j2, …, c_jn), 是隐含层第j个径向基函数的中心矢量; σ_j=(σ_j1, σ_j2, …, σ_jn)是隐含层第j个神经元的归一化参数, 用来确定隐含层第j个神经元对其输入矢量X之间距离响应的面积宽度; j =1, 2, …, m(m为隐含层神经元个数)。 则网络的输出为

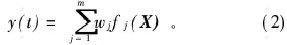
其中: w_j是隐含层第j个神经元节点到输出层的连接权值。 由式(2)可见, RBF神经网络是通过非线性基函数的线性组合实现从Rⁿ到R^m的非线性影射。

2.2 基于遗传算法的网络训练

RBF神经网络训练的关键是根据给定训练样本, 快速有效地确定径向基函数的中心位置、 宽度和输出层权值等有关参数的估计。 遗传算法是模拟生物的进化过程, 根据许可的计算时间, 运用遗传算子对群体优化, 同时以全局并行搜索技术来搜索优化群体中的最优个体, 以求得满足要求的最优解或准最优解^{13-15]。 它是基于最优竞争机制的概率搜索算法。 利用遗传算法优化RBF神经网络时, 一般需要编码, 确定种群规模, 确定适应度函数, 选择操作, 交叉操作, 变异操作以及确定终止条件等几个步骤来实现。 具体的算法如下。

2.2.1 编码

遗传算法编码常用的有二进制编码或实数编码。 这里采用实数编码, 以避免采用二进制编码时, 因过多的估计参数导致码字很长, 从而与精度要求相矛盾的问题。 RBF神经网络的结构参数包括径向基函数的中心位置c_ji、 宽度σ_ji和输出层权值w_j等。 其中: i=1, 2, …, n; j =1, 2, …, m, 待估计参数个数为2mn+m。 个体G_θ编码为:

G_θ={(w₁, …, w_m, c₁₁, …, c_1n, c_m1, …, c_mn,

σ₁₁, …, σ_1n, σ_m1, …, σ_mn}|w_j, c_ji, σ_ji∈R;

i=1, 2, …, n; j=1, 2, …, m}

2.2.2 种群规模

种群的规模直接影响遗传算法的最终结果以及算法的执行效率。 若种群太小, 则容易陷入局部最优解, 优化效果不良; 而若种群太大, 则计算复杂度提高, 不利于求解。 根据经验, 这里取种群规模为P_size=10, 即有P={G_<sub>θk|k=1, 2, …, P_size}。

2.2.3 适应度函数

适应度函数是算法对个体G_θ“好坏”的评价标准, 取值为正。 这里采用RBF神经网络的目标函数作为适应度函数, 即

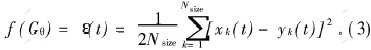
其中: x_k(t)为光纤陀螺的实际输出值; y_k(t)为神经网络的预测输出值; N_size为训练样本个数。

2.2.4 竞争

以初始种群中根据适应度函数选拔出来的最优个体作为优胜者, 具有惟一的与种群中其他个体交叉的权利; 新产生的个体与优胜者竞争, 失利一方作为普通个体。

2.2.5 遗传算子

包括选择, 交叉和变异。 选择是指普通个体按照与适应度函数相关联的概率淘汰, 并由随机产生的新个体取代, 以维持原有的种群规模。 个体G_θ遭遇淘汰的概率为

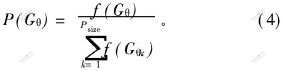
交叉采用单点交叉方式, 以相等的概率(0.5)决定前交叉或后交叉。 1次交叉只产生1个后代个体, 并用该个体替换适应度较低的1个父代个体。 变异采用按位变异。 产生变异有2种情形: 一种是个体的编码与当前优胜者编码相同时, 通过变异, 避免算法早熟; 另一种是普通个体以0.2的概率进行变异。

采用最优竞争机制的遗传算法流程图如图3所示。 种群中个体数量为11个, 其中10个为普通个体, 1个为通过最优竞争挑选出来的优胜者个体。 当连续40代循环没有能够产生新的最优个体时, 结束算法。

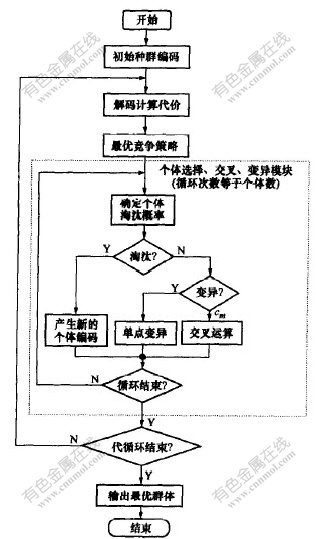
图 3   基于最优竞争机制的GA流程图

Fig. 3   Flow chart of GA based on elitist rule

3 实验方法与结果

3.1 实验方法

为了实现光纤陀螺漂移的误差补偿, 将光纤陀螺的输出角速率作为神经网络的输入, 并取电控转台的旋转角速率作为参考输出, 对不同温度不同旋转角速率下光纤陀螺的输出进行采样。 测试电动转台的转动速度在-25~25 (°)/s范围内以5 (°)/s的间隔作为1个测量点, 陀螺上电后从环境温度逐步上升到1个稳定温度, 通过改变陀螺工作环境温度, 测得温度变化范围为10~40 ℃的数据, 从中选取温度变化间隔为0.1 ℃的100个数据之和作为训练样本, 从而获得神经网络的训练样本集。 利用遗传算法对RBF神经网络进行训练, 调整RBF神经网络的参数, 使RBF神经网络的输出与训练样本集的参考输出之间的误差最小。 当训练完成后, 由于RBF神经网络有良好的泛化能力(即具有插值特性), 系统即可利用该进化神经网络进行补偿。 为了检验训练好的神经网络的灵敏度和容错能力, 利用自行研制的移动机器人样机对用神经网络预测补后的光纤陀螺进行校验。

3.2 实验结果分析

训练神经网络的误差指标为误差平方和(sum-squared error), 图4所示为RBF神经网络的训练结果。 由训练结果可以看出, 采用遗传算法训练RBF神经网络具有较好的收敛效果。 经过261代的优化后, 误差已经收敛到足够小。

经测试, 用该神经网络补偿前, 温度由10 ℃变化到45 ℃, 光纤陀螺角速率输出与温度之间呈现出一定程度的非线性。 陀螺的漂移变化达15~26 (°)/h, 若不进行补偿, 而对移动机器人的导航定位将产生很大的误差。 而经过神经网络补偿后, 在同样的测试条件下, 陀螺的漂移变化控制在3~6 (°)/h, 已经接近于该公司提供的在恒温条件下该产品的测试输出标准(2~4 (°)/h)。 图5所示为应用训练好的神经网络对不同温度段下的光纤陀螺在1 h内的漂移误差进行补偿的结果。 显然, 该神经网络较好地获得了光纤陀螺的输出与温度之间联系的知识, 表明网络具有较强的学习和泛化能力。 经过神经网络对光纤陀螺的温度敏感度特性进行补偿, 大幅度地减少了环境温度变化下光纤陀螺的漂移, 为实现移动机器人准确的航向推算奠定了基础。

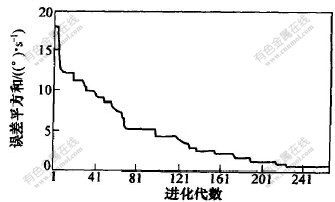
图 4   RBFNN的训练结果

Fig. 4   Training results of RBFNN

图 5   不同温度下进化神经网络校正后的光纤陀螺的输出

Fig. 5   Output of FOG with evolutionary neural network calibration at different temperatures

4 结 论

在光纤陀螺误差分析及常规校正研究基础上, 提出利用RBF神经网络和遗传算法所构建的进化神经网络实现光纤陀螺漂移误差模型的辨识, 大大提高了光纤陀螺的稳定性和抗干扰能力, 从而降低了光纤陀螺的误差影响, 提高了移动机器人导航的定位精度。 通过实验, 证明了应用性能优良的RBF神经网络可以很好地对光纤陀螺漂移所造成的移动机器人航向误差进行校正。

参考文献:

[1]蔡自兴, 贺汉根, 陈虹. 未知环境中移动机器人导航控制研究的若干问题[J]. 控制与决策, 2002, 17(4): 385-390, 464.

CAI Zi-xing, HE Han-gen, CHEN Hong. Some issues for mobile robot navigation under unknown environments[J]. Control and Decision, 2002: 17(4): 385-390, 464.

[2]Barshan B, Durrant-Whyte H F. Inertial navigation systems for mobile robots[J]. IEEE Transactions on Robotics and Automation, 1995, 11(3): 328-342.

[3]Borenstein J. Experimental evaluation of a fiber optics gyroscope for improving dead-reckoning accuracy in mobile robots[A]. IEEE International Conference on Robotics and Automation[C]. Leuven: IEEE, 1998. 3456-3461.

[4]Bennett S M, Emge S, Dyott R. Fiber optic gyros for robotics[J]. American Institute of Aeronautics & Astronautics, 1998, 44(1): 1315-1321.

[5]Chung H, Ojeda L, Borenstein J. Accurate mobile robot dead-reckoning with a precision-calibrated fiber optic gyroscope[J]. IEEE Transaction on Robotics and Automation, 2001, 17(1): 80-84.

[6]朱光辉. 在移动机器人定位中光纤陀螺仪的误差分析与建模[D]. 长沙: 中南大学信息科学与工程学院, 2004.

ZHU Guang-hui. Analysis and Modelling of FOG’s Drift in Mobile Robot’s Localization[D]. Changsha: School of Information Science and Engineering, Central South University, 2004.

[7]蒙祖强, 蔡自兴. 一种基于并行遗传算法的非线性系统辨识方法[J]. 控制与决策, 2003, 18(3): 368-370.

MENG Zu-qiang, CAI Zi-xing. Identification method of nonlinear systems based on parallel genetic Algorithm[J]. Control and Decision, 2003, 18(3): 368-370.

[8]Amir F A, Samir I S. A comparison between neural network forecasting techniques-case study: river flow forecasting[J]. IEEE Transactions on Neural Networks, 1999, 10(2): 402-409.

[9]李英, 李武, 王浣尘. 一种基于演化神经网络的预测算法[J]. 预测, 2003, 22(6): 66-69.

LI Ying, LI Wu, WANG Huan-chen. A forecasting algorithm based on evolutionary neural network[J]. Forecasting, 2003, 22(6): 66-69.

[10]王小平, 曹立明. 遗传算法—理论、 应用与软件实现[M]. 西安: 西安交通大学出版社, 2002.

WANG Xiao-ping, CAO Li-ming. Genetic Algorithm-theory, Application and Software Realization[M]. Xi′an: Xi′an Jiaotong University Press, 2002.

[11]KVH Industries Inc. Core 1000 Fiber Optic Gyro Technical Manual[R]. Middletown: KVH Industries Inc, 1999.

[12]何友, 王国宏, 陆大纟金, 等. 多传感器信息融合及应用[M]. 北京: 电子工业出版社, 2000.

HE You, WANG Guo-hong, LU Da-jin, et al. Multisensor Information Fusion with Applications[M]. Beijing: Electronics Industry Press, 2000.

[13]郑丕谔, 马艳华. 基于RBF网络的递阶遗传训练新方法[J]. 控制与决策, 2000, 15(2): 165-168.

ZHENG Pi-e, MA Yan-hua. A new hierarchical geneti algorithm for training of RBF neural networks[J]. Control and Decision, 2000, 15(2): 165-168.

[14]邹小兵, 蔡自兴. 基于传感器信息的环境非光滑建模与路径规划[J]. 自然科学进展, 2002, 12(11): 1188-1192.

ZOU Xiao-bin, CAI Zi-xing. Non-smooth environment modeling and global path planning based on the sensory information[J]. Progress in Natural Science, 2002, 12(11): 1188-1192.

[15]姜静清, 宋初一, 刘娜仁, 等. RBF神经网络的训练方法与分析[J]. 内蒙古民族大学学报, 2003, 18(4): 301-303.

JIANG Jing-qing, SONG Chu-yi, LIU Na-ren, et al. Training method of RBF neural network and its analysis[J]. Journal of Inner Mongolia University for Nationalities, 2003, 18(4): 301-303.

收稿日期:2005-01-28

基金项目:国家自然科学基金资助项目(60234030)

作者简介:于金霞(1974-), 女, 河南焦作人, 博士研究生, 从事智能控制、 移动机器人定位与环境建模等研究

论文联系人: 于金霞, 女, 博士研究生; 电话: 0731-2655993(O); E-mail: melissa2002@163.com