Al-6.2Zn-0.70Mg-0.30Mn-0.17Zr合金基于Arrhenius模型与ANN模型的热压缩流变行为
来源期刊:中国有色金属学报(英文版)2017年第3期
论文作者:严杰 潘清林 李安德 宋文博
文章页码:638 - 647
关键词:铝合金;热压缩变形;流变应力;本构方程;人工神经网络模型
Key words:aluminum alloy; hot compressive deformation; flow stress; constitutive equation; artificial neural network model
摘 要:在Gleeble-3500热模拟仪上进行热压缩实验,研究在变形温度为623~773 K、应变速率为0.01~20 s-1时均匀化状态下Al-6.2Zn-0.70Mg-0.30Mn-0.17Zr合金的热变形行为。实验结果表明:变形过程中流变应力值随应变速率的减小或变形温度的升高而减小。为研究热压缩过程合金的流变行为,同时建立了应变补偿本构模型与人工神经网络模型。计算结果表明:热压缩过程中各个材料常数与应变之间的关系可分别用6次多项式描述;隐含层含有16个神经元的神经网络模型具有好的预测效果。采用应变补偿本构模型和神经网络模型对流变应力进行预测,预测值平均绝对误差分别为3.49%和1.03%,神经网络模型预测精度与效率均高于应变补偿本构模型。
Abstract: The hot deformation behavior of Al-6.2Zn-0.70Mg-0.30Mn-0.17Zr alloy was investigated by isothermal compression test on a Gleeble-3500 machine in the deformation temperature range between 623 and 773 K and the strain rate range between 0.01 and 20 s-1. The results show that the flow stress decreases with decreasing strain rate and increasing deformation temperature. Based on the experimental results, Arrhenius constitutive equations and artificial neural network (ANN) model were established to investigate the flow behavior of the alloy. The calculated results show that the influence of strain on material constants can be represented by a 6th-order polynomial function. The ANN model with 16 neurons in hidden layer possesses perfect performance prediction of the flow stress. The predictabilities of the two established models are different. The errors of results calculated by ANN model were more centralized and the mean absolute error corresponding to Arrhenius constitutive equations and ANN model are 3.49% and 1.03%, respectively. In predicting the flow stress of experimental aluminum alloy, the ANN model has a better predictability and greater efficiency than Arrhenius constitutive equations.
Trans. Nonferrous Met. Soc. China 27(2017) 638-647
Jie YAN1, Qing-lin PAN1, An-de LI2, Wen-bo SONG2
1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;
2. Suntown Technology Group Co., Ltd., Changsha 410200, China
Received 14 December 2015; accepted 24 December 2016
Abstract: The hot deformation behavior of Al-6.2Zn-0.70Mg-0.30Mn-0.17Zr alloy was investigated by isothermal compression test on a Gleeble-3500 machine in the deformation temperature range between 623 and 773 K and the strain rate range between 0.01 and 20 s-1. The results show that the flow stress decreases with decreasing strain rate and increasing deformation temperature. Based on the experimental results, Arrhenius constitutive equations and artificial neural network (ANN) model were established to investigate the flow behavior of the alloy. The calculated results show that the influence of strain on material constants can be represented by a 6th-order polynomial function. The ANN model with 16 neurons in hidden layer possesses perfect performance prediction of the flow stress. The predictabilities of the two established models are different. The errors of results calculated by ANN model were more centralized and the mean absolute error corresponding to Arrhenius constitutive equations and ANN model are 3.49% and 1.03%, respectively. In predicting the flow stress of experimental aluminum alloy, the ANN model has a better predictability and greater efficiency than Arrhenius constitutive equations.
Key words: aluminum alloy; hot compressive deformation; flow stress; constitutive equation; artificial neural network model
1 Introduction
As one of low Cu-containing alloys in 7xxx series, in addition to good oxidation resistance, low density and high strength, Al-Zn-Mg alloy has greater resistance to stress corrosion cracking (SCC) and better welding performance compared with the other high Cu-containing aluminum alloys, which has been extensively used in the components of automobile and high speed train. However, hot workability of components, which is directly influenced by deformation temperature, strain rate and strain, is one of the most important causes of the wide use of these alloys [1-4].
In the past few decades, the theory of Arrhenius constitutive equations has been proven to be an available approach to investigate the relationship among deformation temperature, strain rate and flow stress during the hot compressive deformation of aluminum alloys. Based on the regression method, constitutive equation is less strictly connected to the deformation mechanisms, so it has been widely applied in practical use and always holds a good performance in establishing the relationship among the deformation parameters. However, the precision of original constitutive equations is limited because they do not consider the effect of strain on flow stress. Therefore, revised constitutive models with the compensation of strain have been proposed by some researchers. LIN et al [5] modified the constitutive models that were then verified by MANDAL et al [6] and SAMANTARAY et al [7] during predicting flow behavior of steels at elevated temperature. In addition, this method was also adopted by ZHAO et al [8] to investigate the flow behavior of Ti600 alloy during hot compressive deformation. The modified models have a better predictability on flow stress. However, due to the non-linear relationships among deformation parameters and the erratic fluctuation of deformation temperature and strain rate during hot compressive deformation, the precision of revised constitutive models is still limited [9-11]. In addition, the material constants must be recalculated after the new deformation parameters are considered. Therefore, the establishment of constitutive equations is a very troublesome question for iterative calculation.
To overcome the disadvantages mentioned above, an artificial neural network (ANN) model, which is unnecessary to derive mathematical model at the beginning, has been successfully applied to predicting elevated temperature flow behavior of metals and alloys. Compared with the constitutive equation, ANN model does not consider the intrinsic physical deformation mechanisms either, but the latter model possesses much stronger ability to handle random data, owing to the readjustment of each neuron’s weight in hidden layer without calculating all the data repeatedly. So, ANN model has been considered as a powerful tool to predict the flow stress of materials under wide range of deformation conditions. Such an ANN model has already been utilized to predict the elevated temperature flow behavior of steels [9], magnesium alloys [10] and aluminum alloys [11]. Unfortunately, although Al-6.2Zn-0.70Mg-0.30Mn-0.17Zr alloy has been used in industry, little research work was focused on the application of constitutive equations and ANN model to characterize hot deformation behavior of this aluminum alloy.
The processing parameters have a great influence on microstructure and macro-performance of aluminum profiles [4]. Predicting the flow behavior of Al-6.2Zn- 0.70Mg-0.30Mn-0.17Zr alloy is of great importance for optimizing its thermo-mechanical process. Accordingly, the present work was to investigate the hot deformation parameters of this aluminum alloy during hot compressive deformation. An Arrhenius model with the compensation of strain and a BP artificial neural network model were established to predict the elevated temperature flow behavior of this aluminum alloy. Furthermore, to compare with Arrhenius model, the performance of these two established models was estimated by correlation coefficient, mean absolute error (MAE) and relative errors.
2 Experimental
The experiments were carried out on Al-6.2Zn-0.70Mg-0.30Mn-0.17Zr alloy produced by semi-continuous casting. The diameter of casting was 260 mm. The chemical composition of the examined alloy is shown in Table 1. Homogenization treatment of ingot was carried out at 738 K for 24 h, and then the ingot was slowly cooled to ambient temperature in air. Before the hot compression tests, the specimen which was derived from the half central area of ingot and was ground, polished and etched with Keller reagent (1.5 mL HCl + 2.5 mL HNO3 + 1 mL HF + 95 mL H2O), was observed by Leica metallographic microscopy. Figure 1 shows the initial microstructure of the alloy consisting of isometric crystal structure, and the calculated average grain size is around 90 μm.
Table 1 Chemical composition of present alloy (mass fraction, %)
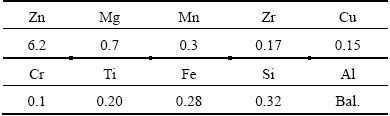

Fig. 1 Initial microstructure of experimental alloy
The hot compression tests were carried out on a Gleeble–3500 testing system. The strain rates were 0.01, 0.1, 1, 10 and 20 s-1 and the deformation temperatures were 623, 673, 723 and 773 K in the experiments. Cylindrical specimens of 10 mm in diameter and 15 mm in height were prepared according to ASTM E209 standard [12]. Before the compression tests, the specimens were heated to deformation temperature with the rate of 10 K/s, then held for 3 min under isothermal conditions to acquire temperature equilibration, afterwards deformed to a true strain of 0.7 which was determined by the actual application.
3 Results and discussion
3.1 Flow behavior and constitutive relationship based on Arrhenius model
3.1.1 True stress-true strain curves
Figure 2 shows the true stress–true strain curves obtained from experiment tests under different deformation conditions. As shown in Fig. 2, the flow behavior of experimental alloy is significantly influenced by deformation conditions. The flow stress increases rapidly with the increase of strain, and the true strain corresponding to steady state flow stress decreases with the decrease of strain rate. Generally, work hardening and dynamic recovery as well as dynamic recrystallization are metallurgical phenomena during the hot deformation process of aluminum alloys [4,13], leading to the complex microstructural evolution which was researched and detailedly illustrated in Ref. [14].
Comparing the values of steady state flow stress under different deformation conditions, it can be found that the steady state flow stress increases with the increase of strain rate or the decrease of deformation temperature. This can be explained that the mobility of dislocation is enhanced at higher deformation temperature. Meanwhile, the time for dislocation reaction is more sufficient when the alloy is deformed at lower strain rate. It is of interest to note that, the oscillations occurred in the curves performed at strain rates of 10-20 s-1 under different deformation temperatures. This phenomenon can be explained in terms of the flow instability such as flow localization or cracking occurred in deformed grains when the strain rate is too high [14]. Moreover, the dislocation glide (DG) is a predominant mechanism of deformation when temperature is low and strain rate is high [15], which causes more inhomogeneous microstructures during hot compressive deformation, leading to flow stress oscillations.
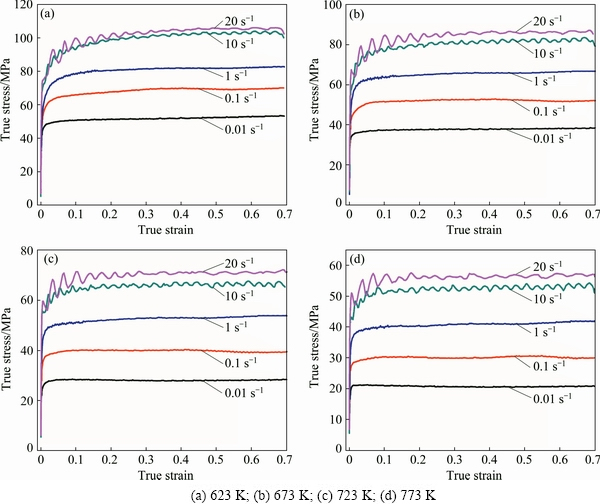
Fig. 2 True stress–true strain curves of alloy
3.1.2 Flow stress prediction by constitutive equations
It has been widely accepted that Arrhenius constitutive equation can be used to express the relationship among the process parameters during the hot compressive deformation of aluminum alloy [16,17]. It can be expressed as
 (1)
(1)
where 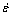 (s-1) is the strain rate, σ (MPa) is the flow stress at a certain deformation temperature, strain and strain rate, T (K) is the thermodynamic temperature, Q (kJ/mol) represents the activation energy for hot deformation, R (8.314 J/(mol·K) and A are the mole gas and material constants, respectively. According to different stress levels, F(σ) can be expressed as
(s-1) is the strain rate, σ (MPa) is the flow stress at a certain deformation temperature, strain and strain rate, T (K) is the thermodynamic temperature, Q (kJ/mol) represents the activation energy for hot deformation, R (8.314 J/(mol·K) and A are the mole gas and material constants, respectively. According to different stress levels, F(σ) can be expressed as
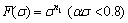 (2)
(2)
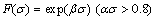 (3)
(3)
 (4)
(4)
where n1, n, β and α are material constants and α can also be defined as α=β/n1. Equations (2) and (3) are suitable for low stress level and high stress level, respectively. However, the hyperbolic-sine (Eq. (4)) proposed by SELLARS and McTEGART [13], is a more general form to describe the stress over a wide range. Therefore, by substituting Eq. (4) into Eq. (1), the following mathematical expression can be obtained:
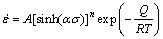 (5)
(5)
To calculate the material constant values, we can combine Eq. (1) with Eq. (2), and Eq. (1) with Eq. (3). Taking the natural logarithm of both sides of these equations, respectively, gives
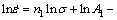 Q/(RT) (6)
Q/(RT) (6)
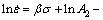 Q/(RT) (7)
Q/(RT) (7)
Hence, constants n1 and β are calculated from the average values of the slopes of ln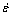 -ln σ plots in the deformation temperature range between 673 and 773 K and
-ln σ plots in the deformation temperature range between 673 and 773 K and  -σ plots in the deformation temperature range between 623 and 723 K, respectively.
-σ plots in the deformation temperature range between 623 and 723 K, respectively.
By taking natural logarithm of both sides of Eq. (5), we can obtain
 Q/(RT) (8)
Q/(RT) (8)
Then, constant n can be calculated from the average values of the slopes of 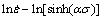 plots. For a given strain rate, differentiating Eq. (8) gives
plots. For a given strain rate, differentiating Eq. (8) gives
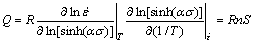 (9)
(9)
So, the activation energy Q can be calculated. The constant S can be calculated from the average values of the slopes of ln[sinh(ασ)]-1000/T plots.
The Zener–Hollomon parameter (Z) can be used to describe the interactive relationship among deformation temperature, strain rate and stress [13,16], which is expressed by
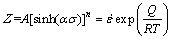 (10)
(10)
where the values of Z under various deformation conditions can be calculated by Eq. (10). After natural logarithm is taken from both sides of Eq. (10), it is transformed into
ln Z=nln[sinh(ασ)]+ln A (11)
Hence, constants n and ln A can be revised and calculated from the slope and intercept of the ln Z-ln[sinh(ασ)] plots, respectively. According to these steps, the values of material constants at a certain true strain can be calculated. By substituting the values of α, Q, n and A into Eq. (1), the constitutive equation can be given, and the flow stresses under different deformation conditions could be predicted.
However, the true strain is not taken into account when the flow stress is predicted by the established model above. Therefore, we need to revise the constitutive equations by incorporating the compensation of strain to make the prediction more precise. The material constants should be expressed as polynomial functions of strain [18]. In order to develop the constitutive equations with strain compensation, the material constants (α, Q, n and ln A) are calculated using data under the deformation strains ranging from 0.05 to 0.65 at an incremental strain of 0.05. Figure 3 shows the relationship between the calculated constant values and true strains. As shown in Fig. 3, three constants α, Q and ln A firstly decreased and then increased slightly with the increase of strain; while the value of n showed a continuous decrease with increasing strain. It can be found that a 6th-order polynomial fitting (as expressed by Eq. (12)) can be applied to describing the influence of strain on material constants, and the fitted lines have a good correlation and generalization. The fitting results of Eq. (12) are listed in Table 2.
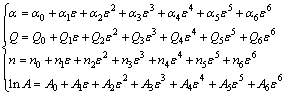 (12)
(12)
As the material constants have been evaluated, the hot deformation behaviors of the alloy can be modelled and the flow stress can be predicted at a particular strain [18], which can be expressed as
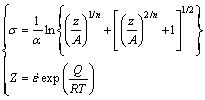 (13)
(13)
3.2 Artificial neural network model
3.2.1 Structure of artificial neural network model
Being a black box approach, artificial neural network (ANN) correlates the input data with the output data using a large class of non-linear functions, and there is no need to develop any mathematical models between input data and output data [19,20]. Therefore, ANN model can effectively serve as a tool to estimate and predict flow stress in hot compressive deformation. A typical ANN model contains one input layer, one output layer and one or more hidden layers [11]. The input layer is used to receive and process input data from outside and send the data to hidden layer; the output layer is used to accept the information from hidden layer and convert results; while in the hidden layer, a series of non-linear functions are used as the transfer function.
A feed-forward back propagation (BP) artificial neural network with Levenberg–Marquardt training algorithm was applied to predicting the flow stress of the experimental aluminum alloy. As for medium size ANN model, the calculation of Levenberg–Marquardt algorithm is fast and efficiency [21]. This makes it easy to recalculate ANN model because the time for ANN model training can be dramatically reduced. For feed-forward network, the errors between experimental and calculated results are calculated and stored, which are used to adjust the weight and threshold of each neuron in hidden layer. This process is network training and validation. After the training process is completed, the weight of each neurons which is used to predict outputs by giving a different set of inputs is stored yet. The three inputs in the present work are temperature (T), strain rate ( ) and strain (ε), and the output is stress (σ). The network architecture is schematically illustrated in Fig. 4.
) and strain (ε), and the output is stress (σ). The network architecture is schematically illustrated in Fig. 4.
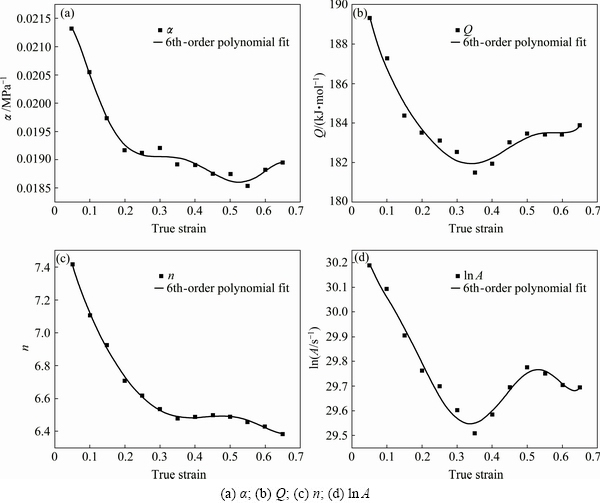
Fig. 3 Relationships between material constants and true strain
Table 2 Coefficients of polynomial fitting curves for material coefficients

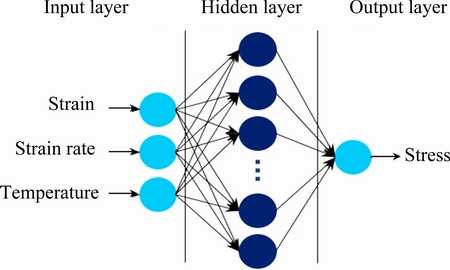
Fig. 4 Schematic illustration of network architecture with one hidden layer
Before the network training, it is necessary to normalize the inputs and outputs data from 0.1 to 0.9 to make the training process more efficient [10,11]. The following equation was widely used for the normalization:
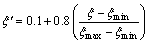 (14)
(14)
where ξ is the original experimental data, ξ′ is the normalized data corresponding to ξ, ξmax and ξmin are the maximum and minimum values of experimental data, respectively. This equation is suitable for normalizing flow stress (σ) and temperature (T) values. Nonetheless, the strain rate (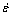 ) changes sharply in this study and this will be harmful to ANN model learning when the strain rate is normalized with Eq. (14). Accordingly, Eq. (15) is utilized to normalize the value of
) changes sharply in this study and this will be harmful to ANN model learning when the strain rate is normalized with Eq. (14). Accordingly, Eq. (15) is utilized to normalize the value of 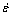 .
.
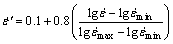 (15)
(15)
Finally, since the data of true strain (ε) is already in the range of 0 to 0.7, there is no need to further normalize. In the current ANN model, a total of 500 input–output pairs were randomly selected from experimental data. Among these data sets, 70% (350) of them were chosen randomly to train the ANN model. The remained 30% (150) input–output pairs which were divided into two equal parts were used to validate the trained ANN model and test the performance of ANN model, respectively. The validation data pairs were used to overcome the over-fitting problem during ANN model training [10]. It is worth noting that the predictability of ANN model is closely associated with the number of neurons in hidden layer. Therefore, the trial-and-error procedure was repeated to identify the number of neurons. Sometimes, it is difficult to find the best weight of each neuron by using optimization methods because the optimum solutions perhaps fall into local optimum [19]. Therefore, average root mean square error (ARMSE) was selected to deal with this problem, which can be expressed as
 (16)
(16)
where ei and ci are the experimental and calculated values, respectively, m is the total number of data employed, j is the training times and is set to 20 in the present work. This means that the ANN model with a fixed number of neurons will repeatedly calculate 20 times. The values of average root mean square error with different number of neurons are shown in Fig. 5. It is found that the ANN model with 16 neurons in hidden layer has the minimum ARMSE, which was taken into consideration.

Fig. 5 Variation of ARMSE with neurons in hidden layer
3.2.2 Performance of well-trained ANN model
The comparison between the experimental flow stresses and the calculated flow stresses is shown in Fig. 6. As can be seen from Fig. 6(a), most of the calculated results were well superposed on experimental flow stresses, which directly illustrated that the ANN model trained before possessed a good performance. In order to further elaborate the performance of the ANN model, Figs. 6(b)-(d) present another form of comparative plots which contain different types of data used in ANN model. For a perfect prediction, the experimental and the calculated values predicted by ANN model should be equal to each other, and all the data sets should lie on the perfect match line. As shown in Figs. 6(b)-(d), all the data points approximately distributed on the perfect match line. Combining with Figs. 6(b) and (c), we can know that the present ANN model is well trained but not over-fitting. From the test results (Fig. 6(d)), we can draw a conclusion that the well-trained ANN model owns a good predication ability.
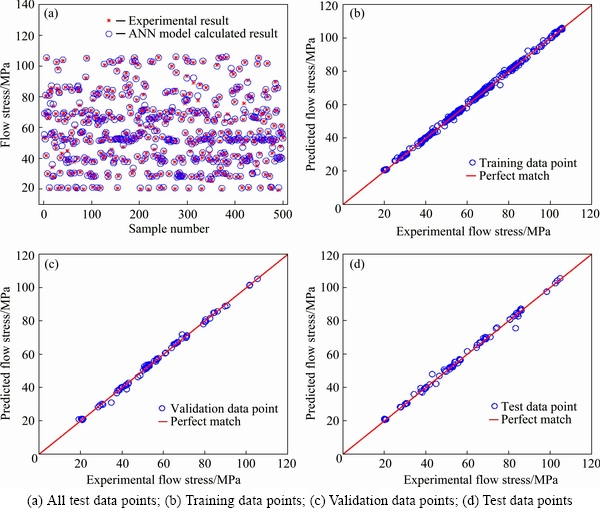
Fig. 6 Comparison between experimental flow stresses and calculated flow stresses
To further quantify the predictability of the ANN model, a series of statistical methods, including correlation coefficient, absolute error as well as the mean absolute error (MAE) were employed in this study [8]. The MAE is defined as
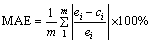 (17)
(17)
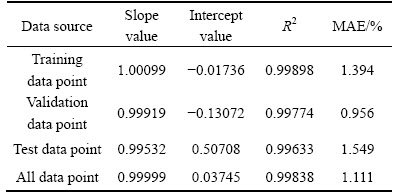
Correlation coefficient (R) is generally utilized to reflect the strength of linear relationship between calculated and experimental results. The value of R ranges from 0 to 1, with near 1 being fitting the data well and near 0 being no linear relationship for the data, and the fitting results of Figs. 6(b)-(d) are listed in Table 3. Combining with the liner fitting results, the slopes of fitting lines and the correlation coefficients are approximately equal to 1. The intercept value of each fitting line is small, close to 0. However, the higher value of R is not a sufficient condition for good performance of the ANN model because the predicted results may be biased towards higher or lower values [19]. Consequently, absolute error and MAE were put forward for evaluating the predictability of the ANN model, and the calculated results are shown in Fig. 7 and Table 3. It can be seen from Fig. 7 that most of absolute errors are less than 4%, and the MAE of each type of data points is less than 2%. Therefore, all the data analyses show that the ANN model with 16 neurons in hidden layer possesses perfect ability to forecast the flow stress of the experimental alloy during hot compressive deformation.
Table 3 Liner fitting results and mean absolute errors of data points
3.3 Comparison between Arrhenius constitutive equations and ANN model
In order to better compare the Arrhenius constitutive equations and ANN model performance, different deformation conditions with strains ranging from 0.05 to 0.65 at an incremental strain of 0.05 were chosen in these two established models. The experimental results and calculated results are shown in Fig. 8. It is revealed that the well-trained ANN model can excellently trace the true stress–true strain curves, indicating that the well-trained ANN model has an admirable predictability. However, as shown in Fig. 8, the flow stress predicted by constitutive equations is not in a good agreement with the whole data set.
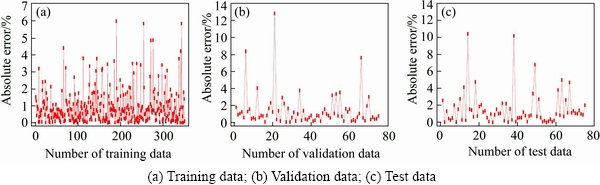
Fig. 7 Absolute errors of samples
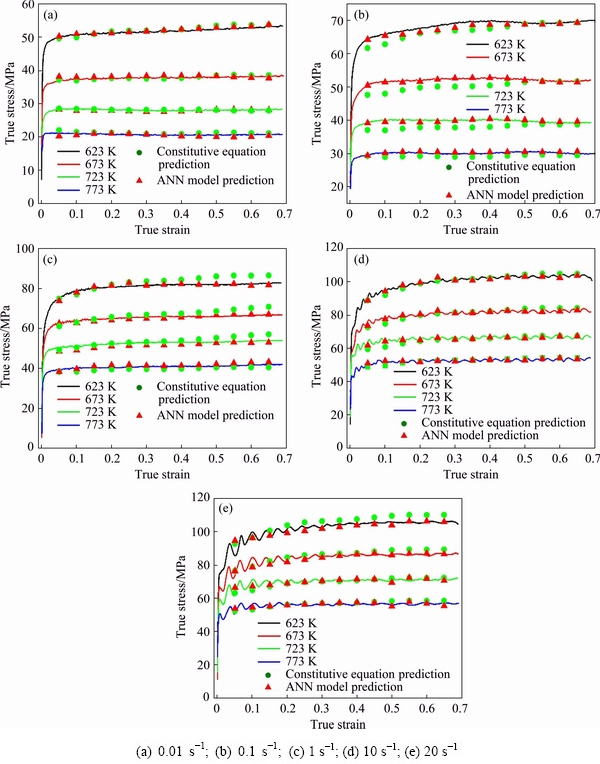
Fig. 8 Comparative plots for experimental (lines) and calculated (dots) results at different strain rates
Figures 9(a) and (b) show another form of comparison between the experimental and calculated results. Similar to the data analysis before, the data closely distributing on perfect match line indicate an excellent predictability. The values of correlation coefficient obtained from constitutive equations and ANN model are 0.986 and 0.998, respectively; the values of MAE are 3.49% and 1.03%, respectively. The MAE of constitutive equations is larger than that of ANN model. These results illustrate that the flow stress predicted by the well-trained ANN model is much more precise.
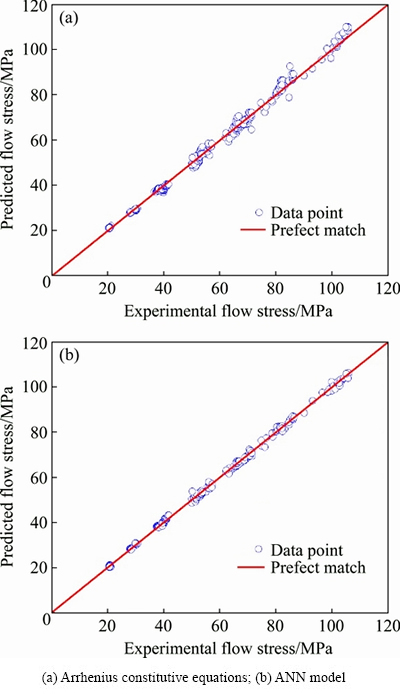
Fig. 9 Evaluation of performance of developed model
Furthermore, the performances of the two established models are evaluated by relative errors. The results are presented in the form of histogram, as shown in Figs. 10(a) and (b). The results show a typical Gaussian distribution. The relative errors calculated by the ANN model vary between -7.048% and 4.470%, while those change from -8.935% to 9.309% by Arrhenius constitutive equations; for more than 98.85% data sets, the relative errors calculated from ANN model was within ±4%, while only 90.77% of the data sets for that of constitutive equations. Therefore, the errors of results calculated by ANN model were more centralized. Moreover, the mean value of relative errors for ANN model is equal to 0.1161%, whereas it is larger (0.1524%) for the constitutive equations. This demonstrates that the flow stresses calculated by constitutive equations are relatively biased towards higher values. Therefore, the constitutive equations with the compensation of strain can be utilized to achieve a superficial estimate for flow stress. On all accounts, all the statistical analysis results indicate that the well-trained ANN model has a better predictability and greater efficiency than the constitutive equations in predicting the flow stress of this aluminum alloy during hot compressive deformation.
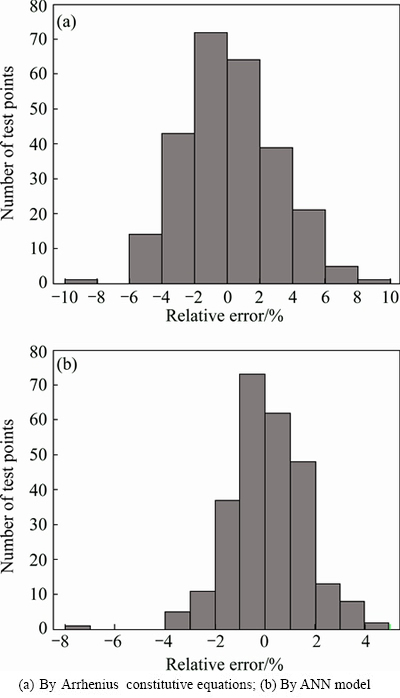
Fig. 10 Statistical analysis of relative errors
4 Conclusions
1) The deformation temperature, strain rate and strain significantly affect the flow stress of the alloy during hot compressive deformation. The flow stress decreases with the increase of deformation temperature and the decrease of strain rate.
2) The values of material constants have relationship with strain. The influence of strain on material constants (α, Q, n and ln A) can be represented by a 6th-order polynomial function.
3) The ANN model with 16 neurons in hidden layer possesses a perfect ability to forecast the flow stress of experimental alloy during hot compressive deformation.
4) The mean absolute errors corresponding to Arrhenius constitutive equations and ANN model are 3.49% and 1.03%, respectively. The errors of results calculated by ANN model are more centralized. In predicting the flow stress of experimental aluminum alloy, the ANN model has a better predictability and greater efficiency than Arrhenius constitutive equations.
References
[1] CHEN Liang, ZHAO Guo-qun, YU Jun-quan. Constitutive analysis of homogenized 7005 aluminum alloy at evaluated temperature for extrusion process [J]. Mater Des, 2015, 66: 129-136.
[2] SHI C J, MAO W M, CHEN X G. Evolution of activation energy during hot deformation of AA7150 aluminum alloy [J]. Mater Sci Eng A, 2013, 571: 83-91.
[3] WANG Ming-liang, JIN Pei-peng, WANG Jin-hui, HAN Li. Hot deformation behavior of as-quenched 7005 aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 2796-2804.
[4] McQUEEN H J, JONAS J J. Plastic deformation of materials [M]. New York: Academic Press, 1975.
[5] LIN Yong-cheng, CHEN Ming-song, ZHONG Jue. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel [J]. Comput Mater Sci, 2008, 42: 470-477.
[6] MANDAL S, RAKESH V, SIVAPRASAD P V, VENUGOPAL S, KASIVISWANATHAN K V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel [J]. Mater Sci Eng A, 2009, 500: 114-121.
[7] SAMANTARAY D, MANDAL S, BHADURI A K. Constitutive analysis to predict high-temperature flow stress in modified 9Cr-1Mo (P91) steel [J]. Mater Des, 2010, 31: 981-984.
[8] ZHAO J W, DING H, ZHAO W J, HUANG M L, WEI D B, JIANG Z Y. Modelling of the hot deformation behaviour of a titanium alloy using constitutive equations and artificial neural network [J]. Comput Mater Sci, 2014, 92: 47-56.
[9] LI H Y, HU J D, WEI D D, WANG X F, LI Y H. Artificial neural network and constitutive equations to predict the hot deformation behavior of modified 2.25Cr-1Mo steel [J]. Mater Des, 2012, 42: 192-197.
[10] SABOKPA O, ZAREI-HANZAKI A, ABEDI H R, HAGHDADI N. Artificial neural network modeling to predict the high temperature flow behavior of an AZ81 magnesium alloy [J]. Mater Des, 2012, 39: 390-396.
[11] LI Bo, PAN Qing-lin, YIN Zhi-ming. Microstructural evolution and constitutive relationship of Al-Zn-Mg alloy containing small amount of Sc and Zr during hot deformation based on Arrhenius-type and artificial neural network models [J]. J Alloys Compd, 2014, 584: 406-416.
[12] ASTM E209. Standard practice for compression tests of metallic materials at elevated temperatures with conventional or rapid heating rates and strain rates [S]. 2010.
[13] SWLLARS C M, McTEGART W J. On the mechanism of hot deformation [J]. Acta Metall, 1966, 14: 1136-1138.
[14] YAN Jie, PAN Qing-lin, LI Bo. Research on the hot deformation behavior of Al-6.2Zn-0.70Mg-0.3Mn-0.17Zr alloy using processing map [J]. J Alloys Compd, 2015, 632: 549-557.
[15] SAKAI T, BELYAKOV A, KAIBYSHEV R, MIURA H, JONAS J J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions [J]. Prog Mater Sci, 2014, 60: 130-207.
[16] REN Fa-cai, CHEN Jun, CHEN Fei. Constitutive modeling of hot deformation behavior of X20Cr13 martensitic stainless steel with strain effect [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 1407-1413.
[17] GHAVAM M H, MORAKABATI M, ABBASI S M. Flow behavior modeling of IMI834 titanium alloy during hot tensile deformation [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 748-758.
[18] LIN Y C, CHEN X M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Mater Des, 2011, 32: 1733-1759.
[19] SMITH M. Neural networks for statistical modelling [M]. New York: Van Nostrand Reinhold, 1993.
[20] HAGHDADI N, ZAREI-HANZAKI A, KHALESIAN A R, ABEDI H R. Artificial neural network modeling to predict the hot deformation behavior of an A356 aluminum alloy [J]. Mater Des, 2013, 49: 386-391.
[21] GUO Z, SHA W. Modelling the correlation between processing parameters and properties of maraging steels using artificial neural network [J]. Comput Mater Sci, 2004, 29: 12-28.
严 杰1,潘清林1,李安德2,宋文博2
1. 中南大学 材料科学与工程学院,长沙 410083;2. 晟通科技集团有限公司,长沙 410200
摘 要:在Gleeble-3500热模拟仪上进行热压缩实验,研究在变形温度为623~773 K、应变速率为0.01~20 s-1时均匀化状态下Al-6.2Zn-0.70Mg-0.30Mn-0.17Zr合金的热变形行为。实验结果表明:变形过程中流变应力值随应变速率的减小或变形温度的升高而减小。为研究热压缩过程合金的流变行为,同时建立了应变补偿本构模型与人工神经网络模型。计算结果表明:热压缩过程中各个材料常数与应变之间的关系可分别用6次多项式描述;隐含层含有16个神经元的神经网络模型具有好的预测效果。采用应变补偿本构模型和神经网络模型对流变应力进行预测,预测值平均绝对误差分别为3.49%和1.03%,神经网络模型预测精度与效率均高于应变补偿本构模型。
关键词:铝合金;热压缩变形;流变应力;本构方程;人工神经网络模型
(Edited by Wei-ping CHEN)
Foundation item: Project (2016GK1004) supported by the Science and Technology Major Project of Hunan Province, China
Corresponding author: Qing-lin PAN; Tel: +86-731-88830933; E-mail: pqlmta102@163.com
DOI: 10.1016/S1003-6326(17)60071-2

