Trans. Nonferrous Met. Soc. China 25(2015) 1648-1656

Analysis and modeling of alumina dissolution based on heat and mass transfer

Shui-qing ZHAN¹, Mao LI¹, Jie-min ZHOU¹, Jian-hong YANG², Yi-wen ZHOU²

1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;

2. Zhengzhou Research Institute, Aluminum Corporation of China Limited, Zhengzhou 450041, China

Received 25 May 2014; accepted 28 August 2014

Abstract: A comprehensive heat and mass transfer model of dissolution process of non-agglomerated and agglomerated alumina particles was established in an aluminum reduction cell. An appropriate finite difference method was used to calculate the size dissolution rate, dissolution time and mass of alumina dissolved employing commercial software and custom algorithm based on the shrinking sphere assumption. The effects of some convection and thermal condition parameters on the dissolution process were studied. The calculated results show that the decrease of alumina content or the increase of alumina diffusion coefficient is beneficial for the increase of size dissolution rate and the decrease of dissolution time of non-agglomerated particles. The increase of bath superheat or alumina preheating temperature results in the increase of size dissolution rate and the decrease of dissolution time of agglomerated particles. The calculated dissolution curve of alumina (mass fraction of alumina dissolved) for a 300 kA aluminum reduction cell is in well accordance with the experimental results. The analysis shows that the dissolution process of alumina can be divided into two distinct stages: the fast dissolution stage of non-agglomerated particles and the slow dissolution stage of agglomerated particles, with the dissolution time in the order of 10 and 100 s, respectively. The agglomerated particles were identified to be the most important factor limiting the dissolution process.

Key words: aluminum reduction cell; alumina particles; dissolution process; heat and mass transfer; finite difference method

1 Introduction

When the alumina is added into a limited zone of molten cryolite bath with modern point feeding technology, it starts to dissolve. The carbon dioxide and liquid molten aluminum are produced by using carbon electrodes because of electrochemical reactions [1]. The effective dissolution of alumina in the cryolite bath is a decisive factor for the stable operation and design of aluminum reduction cells. The part of alumina undissolved in charging forms muck, bottom sludge or crust (essentially solidified sludge) that can affect the velocity profile and the current distribution in liquid molten aluminum and decrease the current efficiency. It is one of the key issues for an advanced aluminium electrolytic process to identify the dissolution mechanism of alumina and improve the dissolution rate of alumina [2,3].

Alumina dissolution in cryolite bath is a very complex phenomenon, in which the bath flow conditions, bath chemical composition, bath temperature, alumina temperature, alumina properties, feeding method, etc., play an important role. Many previous high temperature electrolysis experiments of alumina dissolution were conducted and some significant progress had been made [4-7]. It was difficult to discern the reasonable and credible reaction mechanism for the dissolution process of alumina. WELCH and KUSCHEL [8] studied crust and alumina powder dissolution in aluminum smelting electrolytes. HAVERKAMP and WELCH [9] used modified fast linear sweep voltammetry to investigate the dissolution mechanism of alumina and several models were formulated. BEREZIN et al [10] proposed an alumina dissolution model to study variations of process variables on the formation and dissolution process of alumina agglomerates in “Virtual Cell” program. POI et al [11] thought that heat transfer control was the determining factor for alumina dissolution. Some other studies of alumina dissolution in the laboratory under conditions similar to those encountered in real cells by KUSCHEL and WELCH [12], LILLEBUEN et al [13], VASYUNINA et al [14] and LIU et al [15] had highlighted that both the rate of heat and mass transfer may have important effects on the dissolution rate of alumina. Nevertheless, most literatures about electrolysis experiments of alumina dissolution required strict premises and certain circumstances, which would affect its forecast accuracy and suitability of application, especially for modern large industrial cells.

In recent years, the computational fluid dynamics (CFD) method had been used to investigate the dissolution behaviors of alumina and it was assumed that the dissolution process was instantaneous when the alumina reached the bath surface [16-19]. However, these studies ignored the key fact that the dissolution process of alumina was complex and very slow, which was related with many factors, as mentioned previously. THOMAS [20] used custom programming algorithm to model the dissolution process of alumina in the electrolytic bath, but some other issues, such as the formation and dissolution process of alumina agglomerates and the influences of some operation parameters were not addressed.

The present work aims to establish a comprehensive heat and mass transfer mathematical model and propose an appropriate finite difference method to solve the dissolution process of alumina particles (non- agglomerated and agglomerated particles) employing commercial software and custom algorithm. Based on the above model, the relationships among alumina content, alumina diffusion coefficient, bath superheat, alumina preheating temperature and the dissolution process of alumina were studied, and some suitable dissolution kinetics parameters of alumina were suggested. Besides, the model and the solving methods were used to solve the dissolution process of alumina in a 300 kA aluminum reduction cell. These solutions can provide a new type of custom control algorithms for the quantitative determination of the heat and mass transfer conditions for the alumina dissolution and serve as a reference for the design and optimization of the alumina point feeding technology.

2 Dissolution mechanism and models of alumina

2.1 Dissolution mechanism of alumina

The alumina dissolution in cryolite bath can be described as a coupled heat and mass transfer process. The alumina powder can be treated as monodisperse smooth spheres each with an initial diameter. In practice, the overall dissolution rate of the added powder will be the result of the individual rates of a number of alumina particle sizes. Actually, the particle sizes will range from single grains to aggregates. On one hand, some of the alumina particles may stay in single dispersed states during the dissolution process, which can be described as non-agglomerated particles. The sizes of non- agglomerated particles change very little, just in the normal range of 20-200 μm [1,9,21]. On the other hand, many aspects such as the initial addition of alumina, the phase of alumina, the temperature of the “cold” alumina, the bath superheat will be involved while the alumina is added into the bath. Therefore, some alumina particles can be penetrated by solidified bath and do not disperse in a short time, which can be described as agglomerated particles. The sizes of agglomerated particles are influenced by parameters such as anode gas induced turbulence, alumina preheating temperature, bath superheat and batch sizes of addition of alumina.

Non-agglomerated particles can dissolve fast if the molten bath contains high alumina contents and the relative contact area to volume ratio is high. The dissolution rate of non-agglomerated particles is obviously controlled by mass transfer. The formation of such agglomerated particles strongly reduces the relative contact area to volume ratio compared with the case if all the alumina grains are dispersed in the state of non-agglomerated particles. The dissolution rate of agglomerated particles is limited by heat transfer because of its highly endothermic characteristic and large energy demand on the bath which is therefore proportional to the dissolution rate.

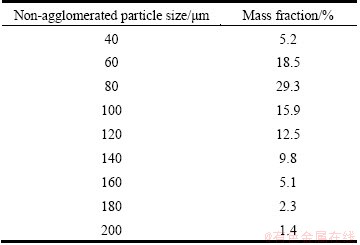
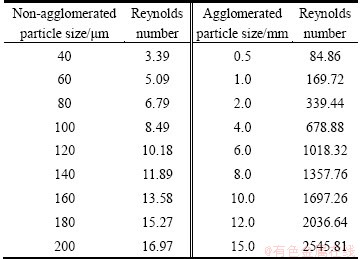
Using the grain size testing instrument from Zhengzhou Research Institute of Aluminum Corporation of China Limited, the initial mass distribution of non-agglomerated particles with respect to the particle diameter was determined as shown in Table 1. As previously explained, it is very difficult to determine the mass distribution of agglomerated particles due to many complicated factors. So far, no such experiment has been reported. For simplification of analysis in this work, the sizes of agglomerated particles were assumed to certain size range, without considering the details of their formation. The agglomerated particles retrieved from the bath were 10 to 50 mm in diameter with a height of 10 to 20 mm [22-24]. In this study, the maximum size of agglomerated particles is defined as 15 mm with sphere diameter for an overall consideration. TAYLOR et al [25] specified that the behavior of agglomerated particles with a diameter of smaller than 400 μm was governed by mass transfer. Therefore, the minimum size of agglomerated particles is set to be 500 μm. Besides, it is assumed that the entire size range of agglomerated particles is divided into nine size groups, which are 0.5, 1.0, 2.0, 4.0, 6.0, 8.0, 10.0, 12.0 and 15.0 mm, respectively.

Table 1 Initial mass distributions of non-agglomerated particles

2.2 Mass transfer model

Equations concerning forced convection mass transfer between fluid and a solid body are usually given as a correlation among the dimensionless Sherwood, Reynolds and Schmidt numbers. For a sphere, the following equation is described by relation in Ref. [26], and can be applied to the free falling non-agglomerated particles in the bath.

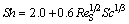                        (1)

where Sh is the Sherwood number calculated by Sh=kd_SD^-1; Re_S is the Reynolds number calculated by Re_S=ρ_Bu_Sd_Sμ_B^-1; Sc is the Schmidt number calculated by Sc=μ_Bρ_B^-1D^-1; k is the mass transfer coefficient; d_S is the non-agglomerated particle diameter; D is the alumina diffusion coefficient; ρ_B is the density of the bath; μ_B is the dynamic viscosity of the bath; the subscript S identifies the non-agglomerated particle.

The terminal free settling velocity of a non-agglomerated particle u_S is in low speed laminar flow area with the Reynolds number Re_S in the range of 3.39-16.97 for u_S being about 0.1 m/s, as shown in Table 2. The latter can be calculated according to the Stokes’ Law [22,26]:

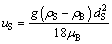                          (2)

where g is the acceleration of gravity; ρ_S is the density of non-agglomerated particles.

The mass transfer rate of single non-agglomerated particle from the surface to the bulk of the bath is

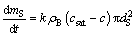                       (3)

where c_sat and c are the saturation alumina content and alumina content, respectively.

The size dissolution rate of non-agglomerated particles based on diameter is defined as

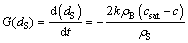               (4)

where G(d_S) is the size dissolution rate of single non-agglomerated particle.

2.3 Heat transfer model

The relationship widely used between the local Nusselt and the local Reynolds number for the free settling of solid particles in liquid flow can be calculated by [26]

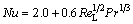                       (5)

where Nu is the Nusselt number calculated by Sh=hd_Lλ_B^-1; Re_L is the Reynolds number calculated by Re_L=ρ_Bu_Ld_Lμ_B^-1; Pr is the Prandtl number calculated by Sc=c_Bμ_Bλ_B^-1; h is the convection coefficient; d_L is the agglomerated particle diameter; λ_B is the thermal conductivity of the bath; c_B is bath specific heat capacity.

The terminal free settling velocity of an agglomerated particle u_L in high turbulence flow area with the Reynolds number Re_L is between 84.86 and 2545.81 for u_L being about 0.2 m/s, as shown in Table 2. Calculation was performed according to the Stokes’ Law [22,26]:

                     (6)

where ρ_L is the density of the agglomerated particles.

The mass transfer rate of single agglomerated particle from the surface to the bulk of the bath can be written as

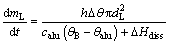                  (7)

where m_L is the mass transfer of agglomerated particles; △θ is the bath superheat calculated by △θ=θ_B-θ_liq; θ_B and θ_liq are the bath and liquidus temperatures, respectively; c_alu is the specific heat capacity of alumina; △H_diss is the enthalpy change for the dissolution plus the phase change.

Table 2 Reynolds number for different non-agglomerated and agglomerated particles

The size dissolution rate of agglomerated particles based on diameter is defined as

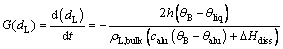 (8)

where ρ_L,bulk is the bulk density of the agglomerated particle; G(d_L) is the size dissolution rate of single agglomerated particle.

2.4 Finite difference numerical solution for dissolution process of alumina

The number of different sizes of non-agglomerated and agglomerated particles can be determined when the initial mass size distribution of alumina and the batch of alumina are known. Therefore, the relationship between the number of alumina particle size per unit volume n(d), the size dissolution rate of single particles G(d) and the total mass transfer ∑m in the domain of the bath Ω can be calculated as

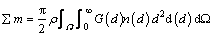           (9)

Thus, the total mass of the alumina particle decreases during the dissolution process.

The mass fraction of non-agglomerated particles P can be expressed as [10]

P=-3.52t_s+58.14                            (10)

where t_s is the complete dissolution time, which is assumed to be 6 min [1,2,9,27].

In this study, a finite difference method employing commercial software and custom algorithm based on shrinking sphere assumption was applied to solving Eq. (9) in the length-based form by considering a dissolution (negative growth) process of alumina particles. Figure 1 shows a sketch of the alumina particle grid. The entire size range of particle is discretized into N small intervals, and the interval between two sizes d_i and d_i+1 is called particle characteristic size △d_i. Every particle size d_i corresponds to a number density of particle n(d_i) and a size dissolution rate of particle G(d_i). Furthermore, an average size dissolution rate G(d)_ave for △d_i can be determined by homogenizing size dissolution rates of its adjacent pivot sizes. So, the mass of alumina particles dissolved △m_i and its corresponding time △t_i from size d_i+1 to d_i of particle size during dissolution process can be calculated as

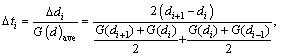
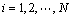          (11)

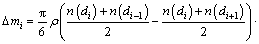
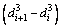                (12)

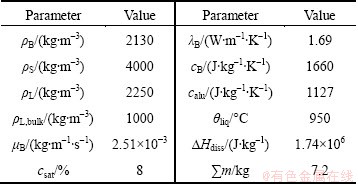
All the analyses of the finite difference numerical solutions described above are suitable to both the dissolution process of the non-agglomerated and agglomerated particles, respectively. Because n(d_i), G(d_i), △t_i and △m_i can be solved dynamically, so all the cumulative masses of alumina particles dissolved will be attained naturally. The important thermodynamic and physical parameters used in the models are given in Table 3.

3 Results and discussion

The main factors that control the dissolution process of alumina include alumina content in the bath, alumina diffusion coefficient in the area within the point feeding zone, bath superheat and alumina preheating temperature. Alumina content and alumina diffusion coefficient that are related to bath convection, mainly affect the dissolution process of non- agglomerated particles. Bath superheat and alumina preheating temperature that are connected to thermal conditions, mainly affect the dissolution process of agglomerated particles. The combination of these four factors determines the overall dissolution process of alumina.

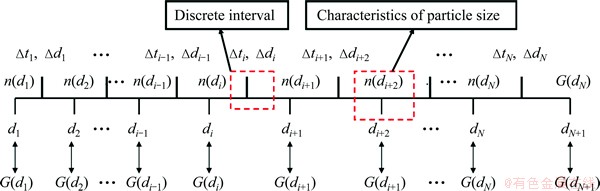
Fig. 1 Sketch of alumina particle grid

Table 3 Thermodynamic and physical parameters of models

3.1 Single parameter effect analysis

3.1.1 Effect of alumina content on dissolution process of non-agglomerated particles

The effect of the alumina content on the dissolution process of non-agglomerated particles was investigated at alumina content of 2%, 3%, 4% and 5%, respectively. In all four variants, a alumina diffusion coefficient of 1.5×10^-9 m²/s was fixed [3]. Figure 2 indicates that the size dissolution rate of non-agglomerated particles decreases with the increase of the alumina content, while dissolution time increases. This is because high alumina content can block the mass transfer from non- agglomerated particles to the bath, which is not beneficial for dissolution process. Under the same alumina content, the size dissolution rate of single non-agglomerated particle firstly decreases and then increases slowly with the increase of non-agglomerated particle size. When the non-agglomerated particle size is larger than 100 μm, its size dissolution rate changes little with the particle size. All the size dissolution rates are of the same order of magnitude, with the value from 4.0×10^-6 to 9.0×10^-6 m/s (Fig. 2(a)). The dissolution time of all the non-agglomerated particles increases approximately linearly on the whole with the increase of non-agglomerated particle size (Fig. 2(b)). Considering for the previously mentioned alumina content between 2% and 5%, the dissolution time is approximately between 25 and 45 s, which is in well accordance with the values of experiments in Refs. [7,15].

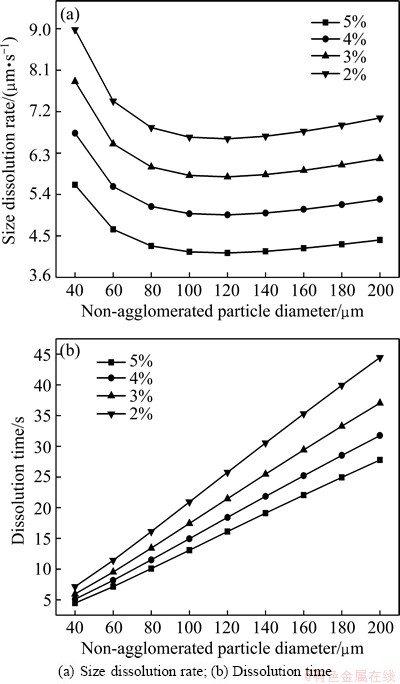
Fig. 2 Effect of alumina content on dissolution process of non- agglomerated particles (D=1.5×10^-9 m²/s)

3.1.2 Effect of alumina diffusion coefficient on dissolution process of non-agglomerated particles

The effect of the alumina diffusion coefficient (D) on the dissolution process of non-agglomerated particles was investigated at alumina diffusion coefficients of 1.5×10^-9, 5.0×10^-9, 1.0×10^-8 and 5.0×10^-8 m²/s, respectively. In this analysis, the alumina content was set to be 3%. The results are shown in Fig. 3. With the increase of alumina diffusion coefficient, the size dissolution rate of non-agglomerated particles increases, and dissolution time decreases. The size dissolution rate of non-agglomerated particles increases nearly 30 times, when D increases from 1.5×10^-9 to 5.0×10^-8 m²/s (Fig. 3(a)). It is indicated that alumina diffusion coefficient has significant effects on dissolution process of non-agglomerated particles. Under the same alumina diffusion coefficient, the size dissolution rate of non-agglomerated particles strictly decreases with the increase of non-agglomerated particle size.

When D is greater than 1.5×10^-9 m²/s, the dissolution time of non-agglomerated particles is significantly reduced; and when D is 5.0×10^-9 m²/s, the dissolution time of non-agglomerated particles is reduced to about 10 s (Fig. 3(b)). The high turbulent conditions in large industrial cells can be obtained due to the strong convection provoked by the motion of anode bubbles and the magnetohydrodynamics effects. Therefore, some better diffusion conditions for alumina dissolution should be considered and the most common approach is the determination of a better feeding point in the cells, such as the crossing points between the centre and the side channels.

3.1.3 Effect of bath superheat on dissolution process of agglomerated particles

In order to determine the effect of bath superheat on dissolution process of agglomerated particles, analyses were carried out at bath superheat of 6, 8, 10, 12 and 15 °C, respectively, under θ_alu of 30 °C. Figure 4 shows the effect of the bath superheat on the dissolution process of agglomerated particles. With the increase of bath superheat, the size dissolution rate of agglomerated particles increases, and dissolution time decreases. This is consistent with the finding that a high bath superheat (△θ=15 °C) gives a high size dissolution rate of agglomerated particles. Increasing bath superheat means that the temperature of the bulk bath increases, which will speed up the heat transport into the agglomerated particles. Consequently, a higher dissolution rate can be gained. Under the same alumina preheating temperature, the size dissolution rate of single agglomerated particles decreases obviously with the increase of agglomerated particle size. Besides, there is a large difference on all of the size dissolution rates of agglomerated particles. It is obvious that the size dissolution rate of the small agglomerated particles increases faster with increasing bath superheat (Fig. 4(a)). Thus, changing the flow path of the anode bubbles could reduce the formation of large agglomerated particles or break up agglomerated particles. When bath superheat increases from 6 to 15 °C, the dissolution time decreases from 640 to 250 s (Fig. 4(b)), which means that bath superheat has a great influence upon the dissolution process of agglomerated particles. The calculated dissolution time is in good agreement with PETER’s result [23], in which the dissolution time of all alumina particles is from about 600 to 360 s.

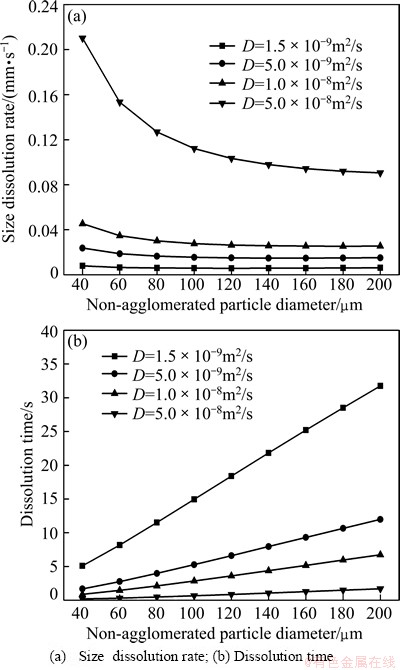
Fig. 3 Effect of alumina diffusion coefficient on dissolution process of non-agglomerated particles (c=3%)

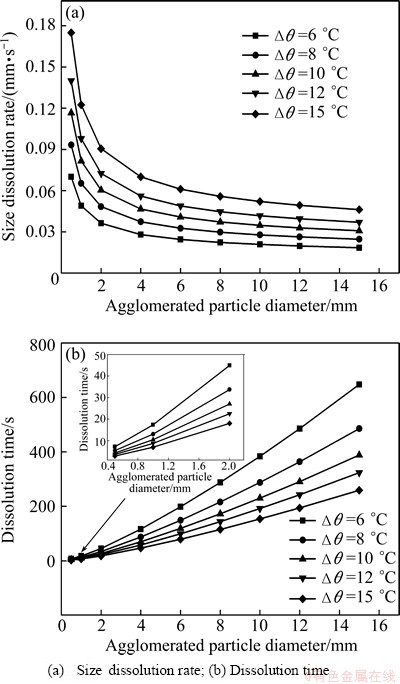
Fig. 4 Effect of bath superheat on dissolution process of agglomerated particles (θ_alu=30 °C)

3.1.4 Effect of alumina preheating temperature on dissolution process of agglomerated particles

The effect of the alumina preheating temperature on the dissolution process of agglomerated particles was determined at alumina preheating temperatures of 30, 100, 200, 300 and 500 °C, respectively, when the bath superheat was set to be 10 °C. Figure 5 reveals that with the increase of alumina preheating temperature, the size dissolution rate of agglomerated particles increases, and dissolution time decreases. But it should be noted that the size dissolution rate of agglomerated particles does not seem to increase much by raising the initial temperature of alumina particles (Fig. 5(a)). Under the same bath superheat, the size dissolution rate of agglomerated particles decreases obviously with the increase of agglomerated particle size. When the alumina preheating temperature increases from 30 to 500 °C, the dissolution time of agglomerated particles decreases from 400 to 310 s (Fig. 5(b)). It can be seen that preheating the alumina particles is not as effective as a higher bath superheat for increasing the dissolution rate and reducing the dissolution time.

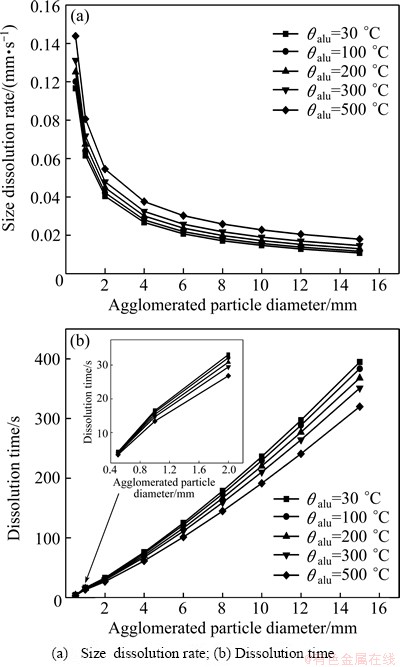
Fig. 5 Effect of alumina preheating temperature on dissolution process of agglomerated particles (△θ=10 °C)

3.2 Comprehensive parameters and effects analysis

The parameters influencing the dissolution process of alumina require a comprehensive analysis, to use the theoretical results for practical optimization of the alumina point feeding technology. Based on the results of the present study, both the decrease of alumina content and the increase of alumina diffusion coefficient can effectively increase the size dissolution rate and decrease the dissolution time of non-agglomerated particles. As bath superheat and alumina preheating temperature increase, the size dissolution rate of agglomerated particles increases and the dissolution time decreases. The dissolution time of non-agglomerated and agglomerated particles is in the order of 10 and 100 s, respectively. It is also found that the alumina diffusion coefficient and bath superheat are more beneficial for the dissolution process of non-agglomerated and agglomerated particles, respectively. For this reason, a high alumina diffusion condition and bath superheat should be properly provided when electrolysis condition permits.

3.3 Application and validation of the model

In this work, the alumina dissolution is applied to a 300 kA industrial aluminum reduction cell for the validation of theoretical model. There are four point feeding hoppers, each with a total batch of 1.8 kg. According to the conservation of mass, alumina is fed in batches of approximately 7.2 kg every 144 s (i.e., normal feeding cycle).

According to the analysis above, the dissolution process of alumina in a normal feeding cycle is studied with the combination of four available operation parameters (c is 3%, D is 4.0×10^-9 m²/s, θ_alu is 30 °C, △θ is 10 °C). As can be seen from Fig. 6, the dissolution process of alumina can be divided into two distinct stages with different rates: the fast dissolution stage of non-agglomerated particles and the slow dissolution stage of agglomerated particles. Approximately 50% (mass percentage) of the batch is dissolved within the first 10 to 15 s, while the rest of the batch is dissolved after 2 min or more. The dissolution rate of the fast dissolution stage is much higher than that of the slow dissolution stage. The agglomerated particles are shown to be the most important factor limiting the dissolution process.

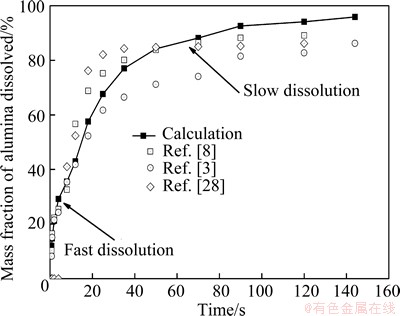
Fig. 6 Comparison of dissolution curve of alumina between calculated results and experimental data

The calculated dissolution curve of alumina (mass fraction of alumina dissolved) is in well accordance with the experimental results from Refs. [3,8,28]. Besides, the complete dissolution of alumina was found to take about 400 s (Fig. 4(b) and Fig. 5(b)), which is almost in agreement with the experimental data (6 min or 360 s) used in this work. Apparently, the calculated result has certain error compared with the laboratory experimental results, and some possible causes are mainly as follows.

1) The dissolution time for all the alumina particles depends heavily on agglomerated particles. It is hard to measure the initial mass distribution of agglomerated particles due to many complicated factors, and so far there have been no relevant experimental measurements reported yet. The hypothetical initial mass distribution of agglomerate particles in this work may be not so accurate.

2) This work ignores the formation of agglomerated particles, but actually it affects the dissolution rate of alumina. Besides, the formation of agglomerated particles in laboratory conditions is not the same as that in industrial conditions. The mass fraction of two kinds of alumina particles would change in different dissolution conditions.

3) The calculated results show that the model is reliable and can be used for complex analysis of the alumina dissolution. The model and algorithms in this study may also be applicable to other systems involving dissolving particles.

4 Conclusions

1) A comprehensive heat and mass transfer model was developed and implemented, in which the alumina is divided into two types: non-agglomerated and agglomerated particles.

2) The results show that both the decrease of alumina content and the increase of alumina diffusion coefficient can effectively increase the size dissolution rate and decrease the dissolution time of non-agglomerated particles. The dissolution time of non-agglomerated particles is in the order of 10 s, and the alumina diffusion coefficient plays a more important role than the alumina content.

3) With the increase of bath superheat and alumina preheating temperature, the size dissolution rate of agglomerated particles increases, while the dissolution time decreases. The dissolution time of agglomerated particles is in the order of 100 s and a higher bath superheat turns out to be more beneficial for a fast dissolution of agglomerated particles.

4) The calculation of a 300 kA aluminum reduction cell shows that the dissolution process of alumina can be divided into two stages with different rates: the fast dissolution stage of non-agglomerated particles and the slow dissolution stage of agglomerated particles. The dissolution rate of the fast dissolution stage is much higher than that of the slow dissolution stage. The agglomerated particles are therefore the most important factor limiting the dissolution process.

References

[1] LIU Ye-xiang, LI Jie. Modern aluminum electrolysis [M]. Beijing: Metallurgical Industry Press, 2008. (in Chinese)

[2] HAVERKAMP R G. Surface studies and dissolution studies of fluorinated alumina [D]. Auckland: University of Auckland, 1992.

[3] KOBBELTVEDT O, ROLSETH S, THONSTAD J. On the mechanisms of alumina dissolution with relevance to point feeding aluminium cells [C]//HALE W. Light Metals 1996. Anaheim, CA: TMS, 1996: 421-427.

[4] ROLSETH R, HOVLAND R, KOBBELTVEDT O. Alumina agglomeration and dissolution in cryolite melts [C]//MANNWEILER U. Light Metals 1994. San Francisco, CA: TMS, 1994: 351-357.

[5] XU Jun-li, SHI Zhong-ning, GAO Bing-liang, QIU Zhu-xian. Dissolution of alumina in molten cryolite [J]. Journal of Northeastern University: Social Sciences Edition, 2003, 24(9): 832-834. (in Chinese)

[6] YANG Zhen-hai, GAO Bing-liang, XU Ning, QIU Zhu-xian, LIU Yao-kuan. Dissolution of alumina in molten cryolite: A video recording study [J]. Journal of Northeastern University: Social Sciences Edition, 1999, 20(4): 398-400. (in Chinese)

[7] KANHong-min,ZHANGNing,WANGXiao-yang. Dissolution rate determination of alumina in molten cryolite based aluminum electrolyte [J]. Journal of Central South University of Technology, 2012, 19(4): 897-902.

[8] WELCH B J, KUSCHEL G I. Crust and alumina powder dissolution in aluminum smelting electrolytes [J]. JOM, 2007, 59(5): 50-54.

[9] HAVERKAMP R G, WELCH B J. Modelling the dissolution of alumina powder in cryolite [J]. Chemical Engineering and Processing, 1998, 37(6): 177-187.

[10] BEREZIN A I, ISAEVA L A, BELOLIPETSKY V M, PISKAZHOVA T V, SINELNIKOV V V. A model of dissolution and heating of alumina charged by point-feeding system in “virtual cell” program [C]//KVANDE H. Light Metals 2005. Warrendale, PA: TMS, 2005: 151-154.

[11] POI N W, HAVERKAMP R G, KUBLER S, STEINHAGEN S M, WELCH B J. Thermal effects associated with alumina feeding in aluminium reduction cells [C]//MANNWEILER U. Light Metals 1994. San Francisco CA: TMS, 1994: 219-225.

[12] KUSCHEL G I, WELCH B J. Further studies of alumina dissolution under conditions similar to cell operation [C]//ROOY E L. Light Metals 1991. San Diego, CA: TMS, 1991: 299-305.

[13] LILLEBUEN B, BUGGE M, HOIE H. Alumina dissolution and current efficiency in  cells [C]//BEARNE G. Light Metals 2009. San Francisco, CA: TMS, 2009: 389-394.

[14] VASYUNINA N V, VASYUNINA I P, MIKHALEV Y G, VINOGRADOV A M. The solubility and dissolution rate of alumina in acidic cryolite aluminous melts [J]. Russian Journal of Non-Ferrous Metals, 2009, 50(4): 338-342.

[15] LIU X M, JENNIFER M P, MARK P T, WELCH B J. Measurement and modeling of alumina mixing and dissolution for varying electrolyte heat and mass transfer conditions [C]//ROOY E L. Light Metals 1991. San Diego, CA: TMS, 1991: 289-298.

[16] FENG Y Q, COOKSEY M A, SCHWARZ M P. CFD modeling of alumina mixing in aluminium reduction cells [C]//JOHNSON J A. Light Metals 2010. Seattle, WA: TMS, 2010: 451-456.

[17] FENG Y Q, COOKSEY M A, SCHWARZ M P. CFD modeling of alumina mixing in aluminium reduction cells [C]//LINDSAY S J. Light Metals 2011. San Diego, CA: TMS, 2011: 543-548.

[18] ZHANG He-hui. Numerical study of vortex flow of melts and transport process of alumina in aluminum reduction cells [D]. Changsha: Central SouthUniversity,2012. (in Chinese)

[19] KAENEL R, ANTILLE J, ROMERIO M V, BESSON O. Impact of magnetohydrodynamic and bubbles driving forces on the alumina concentration in the bath of an  cell [C]//SADLER B. Light Metals 2013. San Antonio, CA: TMS, 2013: 585-590.

[20] THOMAS H. Numerical simulation and optimization of the alumina distribution in an aluminium electrolysis pot [D]. Lausanne:  Polytechnique  de Lausanne, 2011.

[21] KOBBELTVEDT O. Dissolution kinetics for alumina in cryolite melts and distribution of alumina in the electrolyte of industrial aluminium cells [D]. Trondheim: Norwegian University of Science and Technology, 1997.

[22] WALKER D. Alumina in aluminium smelting and its behaviour after addition to cryolite-based electrolytes [D]. Toronto: University of Toronto, 1993.

[23] PETER N. Evolution of alpha phase alumina in agglomerates upon addition to cryolitic melts [D]. Trondheim: Norwegian University of Science and Technology, 2002.

[24] DASSYLVAR V, KISS L I, PONCSAK S, CHARTRAND P, BILODEAU J F, GUERARD S. Modeling the behavior of alumina agglomerate in the  process [C]//GRANDFIELD J. Light Metals 2014. San Diego, CA: TMS, 2014: 603-608.

[25] TAYLOR M P, WELCH B J, ROLSETH S, THONSTAD J. On alumina phase change on the stability of aluminium smelting cells [J]. Journal of AICHE, 1986, 32(5): 1459-1465.

[26] BIRD R B, STEWARD T J, LIGHTFOOT E N. Transport phenomena [M]. New York: John Wiley Sons Inc, 1960.

[27] WALKER M L, PURDIE J M, POI N S, WELCH B J, CHEN J J J. Design considerations the number of the feedings in modern reduction cells [C]//EVANS J. Light Metals 1995. Anaheim, CA: TMS, 1995: 363-370.

[28] KUSCHEL G I. The effect of alumina properties and smelter operation conditions on the dissolution behaviour of alumina [D]. Auckland: University of Auckland, 1990.

基于传热传质的氧化铝溶解过程分析和建模

詹水清¹，李 茂¹，周孑民¹，杨建红²，周益文²

1. 中南大学 能源科学与工程学院，长沙 410083；

2．中国铝业股份有限公司 郑州研究院，郑州 450041

摘  要：基于铝电解槽熔体内氧化铝溶解过程动力学机理，提出了综合的传热传质控制模型，以描述未结块和结块氧化铝颗粒的溶解过程。基于相关商业软件和自定义算法，并结合颗粒收缩核模型，采用合适的差分求解方法，对氧化铝颗粒溶解速率、溶解时间和溶解质量进行计算，探讨若干对流和热条件参数对氧化铝溶解过程的影响。结果表明：降低氧化铝浓度和增大氧化铝扩散速率可以增大未结块颗粒溶解速率，减少未结块颗粒溶解时间；提高电解质过热度和氧化铝预热温度可以增大结块颗粒溶解速率，减少结块颗粒溶解时间。对某300 kA铝电解槽内氧化铝溶解过程进行计算分析，得到的氧化铝溶解质量比例曲线数据与文献结果比较接近；氧化铝溶解过程主要分为两个阶段：未结块颗粒的快速溶解和结块颗粒的缓慢溶解，溶解时间数量级大小分别大约为10和100 s；结块颗粒是影响整个氧化铝溶解过程的最主要因素。

关键词：铝电解槽；氧化铝颗粒；溶解过程；传热传质；差分求解方法

(Edited by Xiang-qun LI)

Foundation item: Project (2010AA065201) supported by the High-tech Research and Development Program of China; Project (2013zzts038) supported by the Fundamental Research Funds for the Central Universities of Central South University, China; Project (ZB2011CBBCe1) supported by the Major Program for Aluminum Corporation of China Limited

Corresponding author: Mao LI; Tel: +86-13055169363; E-mail: limao89@163.com

DOI: 10.1016/S1003-6326(15)63770-0