J. Cent. South Univ. Technol. (2011) 18: 2080-2084
DOI: 10.1007/s11771-011-0946-5
Computational simulation of convective flow in the Earth crust under consideration of dynamic crust-mantle interactions
ZHAO Chong-bin(赵崇斌)1, PENG Sheng-lin(彭省临)1, LIU Liang-ming(刘亮明)1, B. E. HOBBS2, A. ORD2
1. Computational Geosciences Research Centre, Central South University, Changsha 410083, China;
2. School of Earth and Environment, The University of Western Australia, Crawley, WA 6009, Australia
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: The finite element method was used to solve fluid dynamic interaction problems between the crust and mantle of the Earth. To consider different mechanical behaviours, the lithosphere consisting of the crust and upper mantle was simulated as fluid-saturated porous rocks, while the upper aesthenospheric part of the mantle was simulated as viscous fluids. Since the whole lithosphere was computationally simulated, the dynamic interaction between the crust and the upper mantle was appropriately considered. In particular, the mixing of mantle fluids and crustal fluids was simulated in the corresponding computational model. The related computational simulation results from an example problem demonstrate that the mantle fluids can flow into the crust and mix with the crustal fluids due to the resulting convective flows in the crust-mantle system. Likewise, the crustal fluids can also flow into the upper mantle and mix with the mantle fluids. This kind of fluids mixing and exchange is very important to the better understanding of the governing processes that control the ore body formation and mineralization in the upper crust of the Earth.
Key words: computational simulation; crustal fluids; mantle fluids; fluid dynamic interaction
1 Introduction
With the birth and development of the emerging computational geoscience discipline, computational simulation methods have been widely used to solve a broad range of geoscience problems [1]. For example, advanced numerical methods have been employed to simulate the following problems: 1) convective magma flow in the mantle [2-6], 2) convective pore-fluid flow in hydrothermal systems within the upper crust of the Earth [7-9], 3) precipitation and dissolution of minerals in pore-fluid saturated porous rock masses [10-13], and 4) fully coupled problems involving material deformation, pore-fluid flow, heat transfer, mass transport and chemical reactions within the crust of the Earth [14]. Although extensive research has been conducted to investigate the effect of convective pore-fluid flow on ore body formation and mineralization within the upper crust of the Earth, little work has been done to understand the effect of dynamic crust-mantle interaction on the convective pore-fluid flow within the crust of the Earth.
It has been widely recognized that mantle convection is the primary mechanism for the transport of heat and mass from the Earth’s deep interior to its surface [6, 15], so that it influences the Earth’s topography, gravitational field, climate system, cycles of glaciation, biological evolution, and formation of mineral and hydrocarbon resources. As a result, mantle convection becomes the fundamental driving force of plate tectonics, formation and drift of continents, volcanism, earthquakes, and mountain building. Since the thickness of the mantle (i.e. a few thousands of kilometers) is much greater than that of the crust (i.e. only a few tens of kilometers), the crust acts as the skin of a huge body in the whole crust-mantle system. From the computational simulation point of view, this large difference in thickness between the mantle and the crust creates a severe difficulty, when the whole crust-mantle system is modeled simultaneously in a computational simulation. For instance, if the finite element mesh is designed to produce a useful solution for the mantle, then it cannot give any meaningful solution to the crust, because the mesh scale is too large to model the details of the crust. On the other hand, if the finite element mesh is designed to simulate the detailed phenomena within the crust, then it may become computationally impractical because a huge number of degrees-of- freedom are created to model the mantle.
To overcome the aforementioned difficulty, current numerical practice is to simulate the crust and mantle separately. If the behavior of the mantle is of interest, an effective mesh is used to model the mantle, while the crust is treated as an upper boundary in the computational model. However, if the detailed phenomenon within the crust is of interest, an effective mesh is used to model the crust, while the dynamic crust-mantle interaction is neglected so that the effect of the crust/mantle interface can be simplified as a bottom boundary of the computational model. This means that due to the significant scale difference between the mantle and the crust, it remains very difficult, if not impossible, to effectively and efficiently simulate the entire crust-mantle system in a computational model. Nevertheless, for the purpose of investigating the dynamic interaction between the crust and the mantle, it is feasible to simulate the whole crust and a significant part of the entire mantle in a computational model. This is the main motivation of this study.
Taking the above considerations into account, the main purpose of the present work is to extend the existing computational methods to the simulation of convective pore-fluid flow within the crust of the Earth including the dynamic crust-mantle interaction. Since the aesthenospheric part of the mantle is in a partially melted state and the lithospheric rock masses are in a solid state (as far as is considered in this study), there is a melting interface between the aesthenosphere and the lithosphere of the Earth. This means that a melting interface between the aesthenosphere and the lithosphere of the Earth needs to be simulated in the corresponding computational model. Physically, it is necessary to deal with a phase change problem; while mathematically and numerically, it is necessary to deal with a moving boundary problem. The related numerical results are reported to illustrate the convective fluid flow and the temperature distribution in the mantle and crust of the Earth, as well as the effect of dynamic crust-mantle interaction on pore-fluid flow in the upper crust of the Earth.
2 Statement of problem and solution method
2.1 Statement of problem
The lithosphere of the Earth is considered to be comprised of fluid-saturated porous medium, whereas the aesthenospheric part of the mantle is considered to be comprised of viscous fluid. Since the upper aesthenospheric part of the mantle is in a partial melt state, the viscosity value of the viscous fluid should be high enough in the analysis. Under these considerations, the steady-state governing equations for the lithosphere of the Earth are expressed as follows [7]:
vi,i=0 (1)
 (2)
(2)
 (3)
(3)
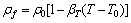 (4)
(4)
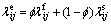 (5)
(5)
where vi is the pore-fluid velocity component in the xi direction; p and T are pore-fluid pressure and temperature; ρ0 and T0 are the reference density of the pore-fluid and the reference temperature used in the analysis; μ and cp are the dynamic viscosity and specific heat of the pore-fluid; 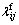 and
and 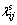 are components of the thermal conductivity tensors for the pore-fluid and solid matrix; f and βT are the porosity of the medium and the thermal volumetric expansion coefficient of the pore-fluid; Kij is the permeability tensor of the medium; gi is the gravity acceleration component in the xi direction.
are components of the thermal conductivity tensors for the pore-fluid and solid matrix; f and βT are the porosity of the medium and the thermal volumetric expansion coefficient of the pore-fluid; Kij is the permeability tensor of the medium; gi is the gravity acceleration component in the xi direction.
On the other hand, the steady-state governing equations for the upper aesthenospheric part of the mantle can be expressed as follows [6]:
ui,i=0 (6)
 (7)
(7)
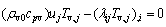 (8)
(8)
 (9)
(9)
where ui is the velocity component of the viscous fluid in the xi direction; pv and Tv are pressure and temperature of the viscous fluid; ρv0 is the reference density of the viscous fluid; μv and cpv are the dynamic viscosity and specific heat of the viscous fluid; λij is the thermal conductivity for the viscous fluid; βvT is the thermal volumetric expansion coefficient of the viscous fluid.
At the melting interface, except for satisfying the pressure and velocity continuity conditions, the temperature and thermal flux continuity conditions should also be satisfied. Since the thermal flux condition at the melting interface involves the latent heat of the rock mass, it provides some extra equations for the problem and therefore, can be used to determine the location of the melting interface. Generally, the temperature and thermal flux continuity conditions at the melting interface can be expressed as
T=Tv (10)
 (11)
(11)
where λn and λvn are thermal conductivities of the pore- fluid and viscous fluid in the normal direction of the melting interface; T,n and Tv,n are thermal gradients of the pore-fluid and viscous fluid in the normal direction of the melting interface, respectively; ρ is the density of the porous rock mass; un is the velocity in the normal direction of the melting interface; L is the latent heat of the porous rock mass.
From the continuum mechanical point of view, both the pore-fluid velocity (i.e. the Darcy velocity) in the porous rock and the viscous-fluid velocity in the upper aesthenospheric part of the mantle are macroscopic quantities. As a result, the following expression exists at the melting interface:
ui=vi (12)
where ui is the i-th component of the viscous-fluid velocity at the melting interface, while vi is the i-th component of the pore-fluid velocity at the melting interface.
Note that as shown in Eqs.(4) and (9), which are based on the well-known Oberbeck-Boussinesq approximation [7], density-driven effects have been considered for both the pore-fluid in the porous rock and the viscous-fluid in the upper aesthenospheric part of the mantle. This indicates that the potential mixing process resulting from the density-driven flow is considered in the computational model.
2.2 Solution method for problem
Due to the complicated and complex nature of the coupled problem described by Eqs.(1)-(11), it is very difficult, if not impossible, to derive analytical solutions to this coupled problem. As an alternative, the computational simulation method is used to solve the coupled problem. The particular solution method selected for solving the related partial differential equations is the finite element method. The reason for this is that the finite element method is one of the most powerful numerical techniques for solving coupled problems between pore-fluid flow/magma flow and heat transfer in either porous media or viscous media. Using the finite element method, not only can the related governing equations of the coupled problem be simulated in an approximate manner, but also the boundary conditions of the coupled problem can be reasonably simulated. Consequently, a numerical solution can be obtained for the coupled problem considered. Generally, the finite element method has the following main advantages. First, hydraulic properties, such as permeability, viscosity and dispersivity, can be easily varied within the computational domain of a system. Second, the complicated and complex geometry of a system, if necessary, can be simulated more efficiently and effectively. Third, the finite element method is easy to understand in concept and straightforward to implement in computation. Fourth, many robust and advanced algorithms have been developed, in recent years, to enable the finite element method to be successfully used for solving a great number of practical engineering problems. Since the finite element method has been well documented in many open publications [1, 16], it is not necessary to repeat it here, for the sake of saving space.
3 Computational simulation results of an example problem
3.1 Description of computational model
In order to examine the effect of the dynamic crust-mantle interaction on the convective pore-fluid flow within the crust of the Earth, the example problem considered in this investigation includes a crust of 35 km, an upper mantle of 115 km and a partial aesthenosphere of 50 km. Note that only a partial part of the aesthenosphere is simulated in the corresponding computational model, for the sake of saving computational efforts. From the material distribution point of view, the crust of the Earth is composed of porous rocks with relatively higher permeability, while the upper mantle of the Earth is mainly composed of porous rocks with relatively low permeability. The aesthenosphere of the Earth is composed of viscous fluids with relatively higher viscosity.
Figure 1 shows the geometry of the computational model for the example problem. The temperature at the top and the bottom of the model is 0 °C and 1 500 °C, respectively. Note that if necessary, a temperature of different value (e.g. 25 °C) can also be assigned at the top of the model, so that the effect of top temperature on the simulation result can be examined in a future study. The partial melting temperature of porous rocks is assumed to be 1 200 °C in the finite element analysis. The dynamic viscosity of the viscous fluid is 1×1020 N·s/m2, while the latent heat of the porous rock mass is 3.5×105 J/kg.

Fig.1 Computational model of example problem
Since the permeability of rock can vary within a wide range, it needs to be carefully determined from geological measurements and observations. This is certainly beyond the scope of this study. To overcome this difficulty, it is feasible to use the previously-available value, as a reference, for estimating the permeabilities of crustal rocks in the computational model [7]. For this reason, the permeability of the rock is assumed to be 1×10-15 m2 and 1×10-16 m2 for the crust and the upper mantle, respectively. The porosity of the rock is 0.1 for both the crust and the upper mantle. The computational domain is simulated using 4 000 four-node quadrilateral elements with 4 141 nodal points in total.
The following parameters are used in the calculation. For the pore-fluid, dynamic viscosity is 10-3 N·s/m2; reference density is 1000 kg/m3; volumetric thermal expansion coefficient is 2.07×10-4 °C-1; specific heat is 4 185 J/(kg·°C); thermal conductivity coefficient is 0.6 W/(m·°C). For the porous matrix, volumetric thermal expansion coefficient is 2.07×10-5 °C-1; thermal conductivity coefficient is 3.35 W/(m·°C); specific heat is 815 J/(kg·°C). For the viscous fluid, volumetric thermal expansion coefficient is 2.07×10-5 °C-1; thermal conductivity coefficient is 3.96 W/(m·°C); specific heat is 1 200 J/(kg·°C); density is 3 300 kg/m3.
3.2 Computational simulation results
Figure 2 shows the distributions of pore-fluid velocity in the lithosphere consisting of the crust and upper mantle, and viscous fluid velocity in the partial aesthenosphere simulated by the computational model. In this figure, arrows are used to represent the fluid velocity vectors, so that the arrow sizes reflect the strength of the fluid flow in the computational model. Similarly, Fig.3 shows the distributions of streamlines for the lithosphere and partial aesthenosphere within the computational model. Due to the relatively high permeability of the crustal rocks, the strongest convective pore-fluid flow (that is shown as a small convection cell of the clockwise direction in Fig.3) takes place within the crust. It can be observed that there exists a large convection cell (of the clockwise direction) within the lithosphere, indicating that there exists a significant dynamic interaction between the mantle fluids and the crustal fluids. Specifically, due to the dynamic crust-mantle interaction, the mantle fluids can flow into the crust and mix with the crustal fluids. Likewise, the crustal fluids can also flow into the upper mantle and mix with the mantle fluids. This kind of fluid mixing is very important to ore body formation and mineralization in the upper crust of the Earth. This indicates that the temperature gradient driven flow, namely the buoyancy driven flow, can carry the precious metal from the mantle and the deeper crust into the upper crust of the Earth.

Fig.2 Distributions of pore-fluid velocity in lithosphere and viscous fluid velocity in partial aesthenosphere
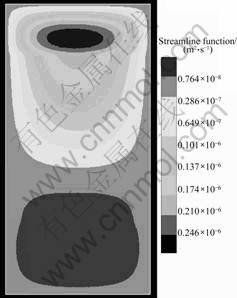
Fig.3 Distributions of streamlines in lithosphere and partial aesthenosphere
Figure 4 shows the distributions of temperature within the computational model, where the temperature difference between two isothermal lines is equal to 150 °C. It is evident that due to the convective pore-fluid flow in the lithosphere, the interface between the crust and the upper mantle is no longer a horizontal line. Similarly, the melting interface, which is usually defined as the isothermal line of 1 200 °C in geology, is also not horizontal. As a result of a convective magma flow cell (of the anti-clockwise direction) occurring in the partial aesthenosphere simulated in the computational model (see Fig.3), the inclination of the crust/mantle interface is different from that of the melting interface in the considered lithosphere-partial aesthenosphere system. As expected from the plate tectonics, the mantle convection indeed takes place in the computational model. When the simulated size of the partial aesthenosphere is increased, the convective magma flow may become stronger in the corresponding computational model.

Fig.4 Temperature distributions within computational model
4 Conclusions
1) The dynamic crust-mantle interaction has a significant effect on the distribution pattern of convective pore-fluid flow in the crust, so that this dynamic interaction should be considered when a reasonable crustal model is established.
2) The mantle fluids can flow into the crust and mix with the crustal fluids, while the crustal fluids can also flow into the upper mantle and mix with the mantle fluids. This kind of fluid mixing is very important to the better understanding of the governing processes behind ore body formation and mineralization in the upper crust of the Earth.
References
[1] ZHAO C, HOBBS B E, ORD A. Fundamentals of computational geoscience: Numerical methods and algorithms [M]. Berlin: Springer, 2009: 241.
[2] RICHTER F M. Convection and large-scale circulation of the mantle [J]. Journal of Geophysical Research, 1973, 78: 8735-8745.
[3] BUCK W R, PARMENTIER E M. Convection between young oceanic lithosphere: Implication for thermal structure and gravity [J]. Journal of Geophysical Research, 1986, 91: 1961-1974.
[4] DOIN M P, FLEITOUT L, CHRISTENSEN U. Mantle convection and stability of depleted and undepleted continental lithosphere [J]. Journal of Geophysical Research, 1997, 102: 2771-2787.
[5] NEIL E A, HOUSMAN G A. Rayleigh-Taylor instability of the upper mantle and its role in intraplate orogeny [J]. Geophysical Journal International, 1999, 138: 89-107.
[6] SCHUBERT G, TURCOTTE D L, OLSON P. Mantle convection in the earth and planets [M]. Cambridge (UK): Cambridge University Press, 2001: 940.
[7] ZHAO C, HOBBS B E, ORD A. Convective and advective heat transfer in geological systems [M]. Berlin: Springer, 2008: 230.
[8] YANG J W. Full 3D numerical simulation of hydrothermal fluid flow in faulted sedimentary basins: Example of the McArthur Basin, Northern Australia [J]. Journal of Geochemical Exploration, 2006, 89: 440-444.
[9] YANG J W, FENG Z, LUO X, CHEN Y. Three-dimensional numerical modeling of salinity variations in driving basin-scale ore-forming fluid flow: Example from Mount Isa Basin, northern Australia [J]. Journal of Geochemical Exploration, 2010, 106: 236-243.
[10] RAFFENSPERGER J P, GARVEN G. The formation of unconformity-type uranium ore deposits: Coupled hydrochemical modeling [J]. American Journal of Science, 1995, 295: 639-696.
[11] ZHAO C, HOBBS B E, M?HLHAUS H B. Finite element modelling of temperature gradient driven rock alteration and mineralization in porous rock masses [J]. Computer Method in Applied Mechanics and Engineering, 1998, 165: 175-187.
[12] GOW P, UPTON P, ZHAO C, HILL K. Copper-gold mineralization in the New Guinea: Numerical modeling of collision, fluid flow and intrusion-related hydrothermal systems [J]. Australian Journal of Earth Sciences, 2002, 49: 753-771.
[13] SORJONEN-WARD P, ZHANG Y, ZHAO C. Numerical modelling of orogenic processes and mineralization in the south eastern part of the Yilgarn Craton, Western Australia [J]. Australian Journal of Earth Sciences, 2002, 49: 935-964.
[14] ZHAO C, HOBBS B E, M?HLHAUS H B. Effects of medium thermoelasticity on high Rayleigh number steady-state heat transfer and mineralization in deformable fluid-saturated porous media heated from below [J]. Computer Methods in Applied Mechanics and Engineering, 1999, 173: 41-54.
[15] ZHAO C, PENG S, LIU L, HOBBS B E, ORD A. Potential mechanisms of pore-fluid movement from the continental lithospheric mantle into the upper continental crust [J]. Journal of Central South University of Technology, 2008, 15(1): 81-88.
[16] ZIENKIEWICZ O C. The finite element method [M]. London: McGraw-Hill, 1977: 787.
(Edited by YANG Bing)
Foundation item: Project(10872219) supported by the National Natural Science Foundation of China
Received date: 2010-10-09; Accepted date: 2011-01-21
Corresponding author: ZHAO Chong-bin, Professor, PhD; Tel: +86-731-88830039; E-mail: chongbin.zhao@iinet.net.au