文章编号：1004-0609(2015)-03-0793-06

全尾砂絮凝沉降速度优化预测模型

王新民，赵建文，张德明

(中南大学 资源与安全工程学院，长沙 410083)

摘  要：建立全尾砂沉降速度GA-SVM优化预测模型，利用遗传学算法对全尾砂沉降速度进行优化预测。建立支持向量机(SVM)回归预测模型，采用训练集对模型进行训练，以验证集预测值的均方误差作为适应度函数，通过遗传算法(GA)对SVM模型参数进行优化选择，应用优化得到的SVM模型对预测集进行预测。以司家营铁矿为例，在絮凝剂单耗8.6 g/t、尾砂浓度18%条件下，沉降速度即可达到1.31 m/h，满足生产需要，比原生产所需絮凝剂单耗减少14%。应用表明：该预测模型具有较高的实用性，为全尾砂沉降速度优化预测提供一种全新思路。

关键词：充填；沉降速度；支持向量机；遗传算法

中图分类号：TD853　　     文献标志码：A

Optimal prediction model of flocculating sedimentation velocity of unclassified tailings

WANG Xin-min, ZHAO Jian-wen, ZHANG De-ming

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Abstract: Based on the GA-SVM optimal prediction model of sedimentation velocity, the genetic algorithm was used to make an optimal predicition. Support vector machine (SVM) regression model was established and trained by the use of samples of training. The acquired mean error of the value was made as a fitness function. Then, the model parameters were optimized through the genetic algorithm (GA). At the end, the optimized SVM was applied to predict the prediction set. GA-SVM optimal prediction mode was used in Sijiaying Iron Mine, the results show that when the flocculating agent consumption and tailings concentration are 8.6 g/t and 18%, respectively, the sedimentation velocity reaches 1.31 m/h. which meet the production requirements. The optimal prediction mode has relatively high practical value, can provide a new method to optimize the sedimentation velocity of unclassified tailings.

key words: backfill; sedimentation velocity; support vectormachine; genetic algorithm

充填采矿法是实现矿山绿色、无废害开采最有效的途径。特别是全尾砂充填采矿法，不仅能提高采矿回收率，降低贫化率，为回收难采矿产资源提供可能性，更重要的是可以解决地表大量全尾砂排放的难题，为减轻尾矿库压力提供有力保障^[1]。在实际生产中，为尽可能减少井下充填排水量，要求充填浆体的浓度尽可能提高，达到膏体或似膏体充填。而选厂排出的全尾砂浆浓度较低，一般仅为10%~25%，无法直接制备高浓度的充填料浆。因此，全尾砂的絮凝沉降成为制约全尾砂高浓度充填的关键因素。

为保证充填系统的连续工作，低浓度的全尾砂浆应能尽快完成絮凝沉降，要求沉降速度越快越好。但沉降速度的提高意味着絮凝剂用量和成本的增加。为此，合理的沉降速度是实现全尾砂充填系统有效、稳定工作的重要参数。传统的研究中，全尾砂沉降速度的选择往往需要进行大量的室内试验。李小斌等^[2]采用Owens二液法各物相的表面自由能，分析赤泥主要物相的表面性质与其沉降性能之间的关系；张钦礼等^[3]通过絮凝沉降试验分析了全尾砂颗粒在浆体中的沉降规律；史秀志等^[4]对多种絮凝剂使用条件下，全尾砂在立式砂仓内的沉降规律进行了研究。但仅通过有限的室内试验，并不一定能得到全尾砂沉降速度的最优值。

支持向量机(SVM)是一种基于结构风险最小化原则的新型回归方法，能较好地解决少数据、频信息、不确定性问题，且不受非线性模型的限制。张钦礼&等^[5]利用SVM建立了充填钻孔寿命优化预测模型；董力通等^[6]对“弹性系数-投入产出”电力需求进行了SVM预测分析；舒服华^[7]提出了一种最小二乘支持向量机的Cu-0.75Gr铜合金反挤压力预测模型。 用LS-SVM对铜铬合金挤压加工挤压力进行了预测。本文作者针对全尾砂沉降速度预测问题，运用SVM进行建模，而针对困扰SVM的模型参数选择问题，结合遗传算法(GA)进行优选，确保所选参数最优化，以保证对全尾砂沉降速度预测的准确性。

1  支持向量机回归模型

SVM^[8-10]的基本原理是利用内积函数定义的非线性变换将输入空间转变为一个高维特征空间，在变换后的高维特征空间中求得输入变量和输出变量之间的一种非线性关系，从而建立SVM预测模型。

已知样本集S={(x₁，y₁)，…，(x_l，y_l)}，l为样本个数，x_i∈Rⁿ；y_i∈R；i=1，2，…，l；n为x_i向量的维数；R为实数集。对于样本空间中的非线性关系，通过变换将输入向量映射到高维特征空间，把寻找最优线性回归超平面的算法归结为求解一个约束条件下的规划问题，从而求得全局最优解。即将原样本集S通过映射f=φ(x)变为高维空间Z，那么对回归问题就转变为，确定一个最优的基于样本集S的函数：

f(x，α)=ωx+b                                (1)

使得|y_i-f(x_i)|≤ε，成立。i=1，…，l；ε为任意小的数；α为拉格兰日乘子；ω为权向量；b为偏置量。S中的点到f(x)的距离d_i：

                         (2)

于是有

d_i≤                              (3)

所以，通过最大化d_i，即最小化||ω||²，就可以得到最优f(x)，此时回归问题化为下面优化问题，考虑到可能误差，引入松弛变量ξ_i，ξ_i^*≥0，i=1，…，l，优化方程为

                    (4)

约束为

f(x_i)-y_i≤ξ_i^*+ε，i=1，…，l                         (5)

y_i-f(x_i)≤ξ_i+ε，i=1，…，l                          (6)

ξ_i，ξ_i^*≥0，i=1，…，l                          (7)

式中：C为惩罚因子。

引入拉格朗日函数

 (8)

式中：α和γ为拉格朗日乘子。

式(8)中分别对ω、ξ和b求偏微分，可得

                     (9)

消去ω和γ后，求出α后，可得f(x)的表达式为

                (10)

故根据Hilbert-Schmidt理论，引入核函数K(x，x_i)=h(x)h(x_i) ^[13]，代入式(10)得到f(x)的表达式为

                     (11)

为避免造成“维数灾难”，选取的核函数为高斯核函数(RBF)：，σ为核函数参数。经过验证，可以使SVM获得平滑的预测。

2  基于GA的SVM预测模型建立

2.1  数据归一化

样本中各个指标的数量级差异较大，在进行计算前，首先对样本中的各向量进行无量纲的归一化处理，公式为

                            (12)

2.2  基于遗传算法的SVM参数寻优

遗传算法极值寻优把训练后的预测结果作为个体适应度值，通过选择、交叉和变异操作寻找函数的全局最优值和对应的输入值^[11-12]。

1) 适应度函数

根据个体得到预测模型的初始权值和阀值，用训练数据训练预测系统输出，把预测输出和期望输出直接的误差绝对值和E作为个体适应度值F，计算公式为

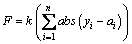                      (13)

式中：n为网络输出节点数，为第i个节点的期望输出；k为系数，为第i个节点的预测输出。

2) 选择操作

遗传算法选择有轮盘赌法，锦标赛法等多种发放，本文作者采用轮盘赌法，即基于适应度比例的选择策略，每个个体i的选择概率p_i为

                                 (14)

                                 (15)

式中：f_i为个体i的适应度值，由于适应度值越小越 好，所以在个体选择前对应适应度求倒数；k系数；N为种群数目。

3) 交叉操作

由于个体采用实数编码，所以交叉操作方法采用实数交叉法，第k个染色体a_k，第l个染色体a_l在j位的交叉操作方法如下：

                          (16)

4) 变异操作

选取第i个个体的第j个基因a_ij进行异变，异变操作方法如下：

           (17)

遗传算法的基本步骤如下。

1) 编码。采用通用的二进制编码法，以σ、C和p 3个参数的二进制编码随机组合构成n组染色体。

2) 选择合适的参数。包括群体大小M(一般取为20~100)，遗传代数T(一般取为100~500)，依据实际数据复杂程度进行选择。

3) 确定适应值函数。根据SVM回归预测模型，要想得到精度高的回归函数，必须使得预测值与实际值的误差尽量小，使回归曲线与实际曲线贴近，因此确定把均方误差作为适应值函数。显然，适应值越小，模型越精确。

4) 随机生成群体。

5) 进行遗传迭代。直到满足停止条件(遗传代数达到)，得到最优SVM参数。

最终得到的GA_SVM结合关系如图1所示。

图1  GA_CV_SVM预测模型

Fig. 1  GA_CV_SVM prediction model

3  应用实例

以司家营铁矿全尾砂充填系统为例，运用GA_SVM模型对全尾砂沉降速度进行预测。大量研究表明，在尾砂的物理力学性质和絮凝剂特性一定的情况下，絮凝剂用量和尾砂浓度是影响絮凝沉降效果的最主要因素。理论上絮凝剂的用量越大，尾砂的沉降速度越快，但用量大，其药剂成本增加，且会造成溢流水中絮凝剂含量高，废水处理困难；絮凝剂用量少，则沉降速度慢，满足不了立式砂仓连续动态放砂的要求，且溢流水中含固量增高，增加废水处理成本。尾砂浓度越高，所含固体颗粒越多，絮凝剂的用量越多，且尾砂颗粒间的相互作用力增加，沉降速度降低；尾砂浓度过低，则造成其最终沉降浓度降低，达不到尾砂使用要求^[13-14]。因此，确定絮凝剂沉降参数主要有絮凝剂单耗q和尾砂浓度c_w(质量浓度，%)可作为主要的影响因素，研究其与全尾砂沉降速度v之间的关系。

3.1  建立样本集

矿山实际生产中，选厂直接排出的全尾砂浆浓度通常为10%~25%，全尾砂浓缩脱水时絮凝剂的添加比例一般为每吨干尾砂添加絮凝剂5~20g。综合考虑据司家营铁矿全尾砂的性质，选择4种比较典型的絮凝剂单耗q和尾砂浓度C_w组合进行正交试验，从而选用可安排二因素、四水试验的正交试验表，试验水平如表1所示。

表1  试验因素与水平

Table 1  Factors and levels in test

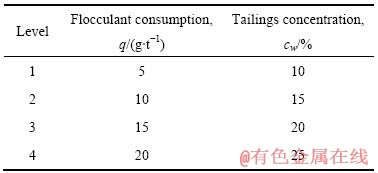
按照试验设计，在实验室通过量筒试验，进行测定其沉降速度。试验过程中通过测定不同时间和沉降界面的高度来计算沉降速度，得到样本数据如表2所列。对样本数据进行归一化处理，所得结果如表3所列。

3.2  GA-SVM模型确立

根据GA-SVM原理，将样本集代入式(10)，求出公式中参数，得到确定的全尾砂沉降速度的GA-SVM预测模型。

表2  参数优选试验结果(样本集)

Table 2  Optimization test result of parameters (samples of training)

表3  归一化处理后的无量纲样本数据

Table 3  Normalized data of normalization

3.3  模型求解

以表3提供的样本数据，运用MATLAB对全尾砂沉降速度GA-SVM预测模型进行计算，可以得出预测输出与期望输出的对比曲线(见图2)。

由图2可以看出，模型的拟合结果良好，预测所得结果与实际值误差较小，模型预测精度较高；全尾砂的沉降速度与絮凝剂单耗、尾砂浓度并不成线性关系，当絮凝剂单耗较小时，沉降速度随浓度的增大而减小。在尾砂浓度较高时，沉降速度随絮凝剂用量的增大而增大。单一的增加絮凝剂单耗和降低尾砂浓度，并不能达到增加沉降速度的要求。

应用遗传算法求解全尾砂沉降速度，遗传算法的迭代次数为50次，种群规模是20，交叉概率0.2，交叉变异概率为0.1，采用浮点数编码^[15-16]，个体长度为2，优化过程中最优个体适应度值变化曲线如图3所示。为满足全尾砂充填系统需要，全尾砂沉降速度应大于1.25 m/h。在此前提下，优选出絮凝剂单耗最小用量。利用遗传算法对全尾砂絮凝沉降预测模型进行求解，由图3可知，预测模型的最优解与实际最大值非常接近，说明了该方法的有效性。最优解为絮凝剂单耗为8.6 g/t，尾砂浓度为18%。此时，全尾砂沉降速度即可达到1.31 m/h，满足生产需求。以预测模型提供的絮凝沉降参数作为实验指导数据，实验结果所得沉降速度为1.32 m/h，与预测模型寻优结果基本一致。

图2  预测输出与期望输出对比图

Fig. 2  Predicted output and desired output

图3  适应度变化曲线图

Fig. 3  Fitness changing

3.4  模型预测结果分析

预测优化结果表明。

1) 遗传学算法在计算过程中，可经过较少的迭代进化，对结果进行优胜劣汰，不断逼近优化解群，并利用待优化指标的试验数据作为适应度函数值。

2) 所建立的絮凝沉降速度预测模型具有较强的预测能力，可以根据输入参数(絮凝剂单耗、尾砂浓度)较精确地预测出沉降速度。根据实际需要，求解出全尾砂沉降速度，试验验证表明求解参数与实际结果具有较高的一致性。

3) 全尾砂的沉降速度与絮凝剂单耗、尾砂浓度并不成线性关系，当过量的絮凝剂加入到全尾砂浆中时，过量的絮凝剂颗粒无法与全部尾砂颗粒发生反应，其本身形成絮凝团，由于其密度小，悬浮于水中，使全尾砂的沉降速度减慢。

综合以上原因，选取司家营铁矿絮凝沉降参数如下：絮凝剂单耗为8.6g/t，尾砂浓度为18%，此时全尾砂在立式砂仓中的沉降速度可达1.31 m/h，沉降效果最好，实际生产需要。相比于实际生产絮凝剂的使用量降低14%，具有较高的经济效益。通过司家营铁矿的生产实践，验证了全尾砂絮凝沉降参数预测模型的实用性，有效降低全尾砂絮凝沉降成本，提高絮凝沉降效果。

4  结论

1) 根据SVM原理，通过简化，建立了以絮凝剂单耗和全尾砂浆体浓度为输入，以沉降速度为输出的GA-SVM预测模型，从而提高了模型的学习和训练速度，减小误差。

2) 通过设计正交试验，产生样本集，运用MATLAB对全尾砂沉降速度GA-SVM预测模型进行计算，所得出的预测输出与期望输出相近。

3) 利用遗传学算法对预测模型进行最优求解，并以预测模型提供的絮凝沉降参数作为实验条件，实验所得结果也预测寻优结果基本一致。

4) 运用全尾砂沉降速度GA-SVM预测模型对司家营铁矿絮凝沉降进行预测优化，避免了传统絮凝沉降参数选择的主观性、随机性，能够做出更为科学、准确、有理论依据的判断。同时，预测模型为矿山全尾砂絮凝沉降参数的选择提供了新的思路和可靠的技术支撑。

REFERENCES

[1] 吴 迪, 蔡嗣经, 杨 威, 王文涛, 王 章. 基于CFD的充填管道固-液两相流输送模拟及试验[J]. 中国有色金属学报, 2012, 22(7): 2133-2142.

WU Di, CAI Si-jing, YANG Wei, WANG Wen-xiao, WANG Zhang. Simulation and experiment of backfilling pipeline transportation of solid-liquid two-phase flow based on CFD[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(7): 2133-2142.

[2] 李小斌, 赵东峰, 章 宣, 刘桂华, 彭志宏, 周秋生. 赤泥主要物相的表面性质对其沉降性能的影响[J]. 中国有色金属学报, 2012, 22(1): 281-286.

LI Xiao-bin, ZHAO Dong-feng, ZHANG Xuan, et al. Effect of surface property of main minerals in red mud on their sedimentation ability[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(1): 281-286.

[3] 张钦礼, 谢盛青, 郑晶晶, 王新民. 充填料浆沉降规律研究及输送可行性分析[J]. 重庆大学学报, 2011(1): 105-107.

ZHANG Qin-li, XIE Sheng-qin, ZHENG Jing-jing, WANG Xin-ming. Sedimentation law research and transportation feasibility study of backfilling slurry[J]. Journal of Chongqing University, 2011(1): 105-107.

[4] 史秀志, 胡海燕, 杜向红, 李茂林, 王怀勇. 立式砂仓尾砂浆液絮凝沉降试验研究[J]. 矿冶工程, 2010(3): 1-3.

SHI Xiu-zhi, HU Hai-ye, DU Xiang-hong, LI Mao-lin, WANG Huai-yong. Experimental study on flocculating sedimentation of tailings slurry in a vertical sand tank[J]. Mining and Metallurgical Engineering, 2010(3): 1-3.

[5] 张钦礼, 陈秋松, 胡 威, 高瑞文. 充填钻孔寿命SVM优化预测模型研究[J]. 中南大学学报: 自然科学版, 2014, 45(2): 536-540.

ZHANG Qin-li, CHEN Qiu-song, HU Wei, GAO Rui-wen. SVM optimal prediction model of the backfill drill-hole life[J]. Journal of Central South University of Technology: Science and Technology, 2014, 45(2): 536-540.

[6] 董力通, 谭显东, 刘伟国, 刘海波. 基于SVM的“弹性系数-投入产生”电力需求预测分析模型[J]. 中南大学学报: 自然科学版, 2012, 43(6): 2442-2444.

DONG Li-tong, TAN Xian-dong, LIU Wei-guo, LIU Hai-bo. Model of forecasting and analysis electricity demand based on SVM of elastic coefficient and input-output[J]. Journal of Xiangtan Normal University: Science and Technology, 2012, 43(6): 2442-2444.

[7] 舒服华. 基于LS-SVM的铜铬合金挤压加工挤压力预测[J]. 中南大学学报: 自然科学版, 2008, 18(9): 1706-1708.

SHU Fu-hua. Prediction model for extrusion force of Cu-0.75Cr alloy based on least square support vector machine[J]. Journal of Central South University of Technology: Natural Science Edition, 2008, 18(9): 1706-1708.

[8] Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction[J] Transactions of Nonferrous Metals Society of China, 2012, 22(2): 433-435.

[9] GHEMTIO L, SOIKKELI A, YLIPERTTULA M, HIRVONEN J, FINEL M, XHAARD H. SVM classification and CoMSIA modeling of UGT1A6 interacting molecules[J]. J Chem Inf Model, 2014, 54(4): 1011-1026.

[10] 杨宏辉, 孙进才, 袁 骏. 基于支持向量机和遗传算法的水下目标特征选择算法[J]. 西北工业大学学报, 2005, 23(4): 512-515.

YANG Hong-hui, SUN Jin-cai, YUAN Jun. A new met ho d for feature selection for underwater acoustic tar gets[J]. J of North western Polytechnical University, 2005, 23(4): 512-515.

[11] 李 杰, 楚 恒, 朱维乐, 彭 静. 基于支持向量机和遗传算法的纹理识别[J]. 四川大学学报, 2005, 37(4): 104-108.

LI Jie, CHU Heng, ZHU Wei-le, PENG Jing. Texture recognition using support vector machines and genetic algorithm[J]. J of Sichuan University, 2005, 37(4): 104-108.

[12] 刘 凯, 黄德镛, 张明旭, 吴东旭. 大红山铜矿全尾砂絮凝沉降的试验研究[J]. 中国矿业, 2008(12): 60-63.

LIU Kai, HUANG De-yong, ZHANG Ming-xu, WU Dong-xu. Experimental study on all tailings flocculation settling in Dahongshan cooper mine[J]. China Mining Magazine, 2008(12): 60-63.

[13] 王 星, 瞿圆媛, 胡伟伟, 韩文亮, 吴 淼. 尾矿浆絮凝沉降影响因素的试验研究[J]. 金属矿山, 2008(5): 149-151.

WANG Xing, QU Yuan-yuan, HU Wei-wei, HAN Wen-ling, WU Miao. Experiment research on factors influencing tailing pulp flocculation settling[J]. Metal Mine, 2008(5): 149-151.

[14] JAE H M, Y C L. Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters[J]. Expert Systems With Application, 2005, 28: 603-614.

[15] 郑春红, 焦李成, 郑贵文. 基于GA的遥感图像目标SVM自动识别[J]. 控制与决策, 2005, 20(11): 1212-1215.

ZHENG Chun-hong, JIAO Li-cheng, ZHENG Gui-wen. Genetic algorithm- based SVM for automatic target classification of remote sensing images[J]. Control and Decision, 2005, 20(11): 1212-1215.

(编辑  李艳红)

基金项目：国家“十一五”科技支撑计划课题：露天境界外驻留矿安全高效开采方法及工艺研究(2008BAB32B03)

收稿日期：2014-05-30；修订日期：2014-12-17

通信作者：王新民，教授，博士；电话：13187011058；E-mail：zhaojianwen0607@qq.com