J. Cent. South Univ. (2019) 26: 673-683

DOI: https://doi.org/10.1007/s11771-019-4038-2

A novel estimation algorithm for torpedo tracking in undersea environment

D. V. A. N. RAVI KUMAR¹, S. KOTESWARA RAO², K. PADMA RAJU³

1. Department of ECE, GVPCEW, Madhurawada, Visakhapatnam-530048, India;

2. Department of ECE, KLEF, Guntur, India;

3. Department of ECE, JNT University, Kakinada, India

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: A novel estimation algorithm is introduced to handle the popular undersea problem called torpedo tracking with angle-only measurements with a better approach compared to the existing filters. The new algorithm produces a better estimate from the outputs produced by the traditional nonlinear approaches with the assistance of simple noise minimizers like maximum likelihood filter or any other algorithm which belongs to their family. The introduced method is extended to the higher version in two ways. The first approach extracts a better estimate and covariance by enhancing the count of the intermediate filters, while the second approach accepts more inputs so as to attain improved performance without enhancement of the intermediate filter count. The ideal choice of the placement of towed array sensors to improve the performance of the proposed method further is suggested as the one where the line of sight and the towed array are perpendicular. The results could get even better by moving the ownship in the direction of reducing range. All the results are verified in the MATLAB environment.

Key words: estimation algorithm; torpedo tracking; angle-only measurements; line of sight; maximum likelihood filter

Cite this article as: D. V. A. N. RAVI KUMAR, S. KOTESWARA RAO, K. PADMA RAJU. A novel estimation algorithm for torpedo tracking in undersea environment [J]. Journal of Central South University, 2019, 26(3): 673–683. DOI: https://doi.org/10.1007/s11771-019-4038-2.

1 Introduction

Tracking is a process of computing the present position of the target. It also involves estimation or anticipation of the future position of the target as close to the true position as possible with the help of the available noisy measurements. The tracking is done with the help of the radar and sonar. Radar stands for radio detection and ranging and it is used to track targets in the air and on land, while the sonar stands for sound navigation and ranging and it is used to track targets in the underwater scenarios. In our paper we are dealing with underwater torpedo tracking so, we are concerned with only the sonar measurements. The sonar can again operate in two modes namely active and passive modes. In active mode of operation of sonar, the principle of operation is that a sound signal will be transmitted towards the target and after some time an echo is heard. Based on the time taken by the signal to travel toward the target and back to us we can find the range of the target and based on the direction from which the echo is received we can find the azimuth at which the target is present. So in active mode of operation of sonar we get both the range and bearing information of the target. The alternate approach is the passive tracking [1, 2] where no signal will be released by us and we will only collect the information from the enemy which is produced by the propellers of the enemy vehicle. Because of this advantage we are concerned only with the passive tracking in this paper. Again the passive mode sonar is supported by a single [3] or multiple sensors [4]. If the sonar uses single sensor, then the lone sensor should be manoeuvring in order to ensure the observability of the target. On the other hand if the sonar uses multiple sensors then these sensors use the concept of triangulation to compute the position of the target. In our paper we are dealing with multiple sensors as in Ref. [5] instead of using a single sensor. Again the multiple sensors are classified into Hull mounted and towed array types. In this research we are dealing with the towed array measurements.

The algorithms which are available in the literature to deal with the above problem are Kalman filter (KF) [6], extended Kalman filter (EKF) [3, 7] and its their variants like modified gain EKF, unscented Kalman filter (UKF) [4, 8, 9] and its variants like integrated UKF, robust UKF, particle filter (PF) [10] and many of its variants [11–13] probability hypothesis density based filters like that in Ref. [14]. A new algorithm called the cubature Kalman filter [15–17] came and showed its speciality in the situation of estimation problems involving large state vectors. Gauss hermite Kalman filter, an algorithm which belongs to the family of cubature Kalman filter, proposed by ARSARATNAM et al [18] makes a useful contribution in the area of tracking. Many other ways of tracking targets in sophisticated situations [19, 20] are proposed. Some of them have the advantage in terms of producing small estimation errors but they struggle in terms of the complexities. On the other hand the algorithms which exhibit superiority in terms of complexities then they struggles in terms of estimation errors. But the algorithm developed in this paper is optimal and produces very less estimation errors at reasonable complexity. The importance of this research is not limited to the target tracking purposes but the work if extended can play a significant role in the other fields like robot tracking [21, 22], video tracking [23], navigation and so on. The complicated tracking environments like the one in Ref. [24] can be supported to a great deal with the suggestions given in this paper.

The principle of operation of the raw form of proposed algorithm is that the refined estimate of the moving target is generated by the fusing algorithm like the maximum likelihood estimator (MLE) or the least squares estimator (LSE). The fusing filter in turn runs with the help of the intermediate estimators which are nonlinear like EKF or UKF. The performance of the proposed method is further improved by optimal positioning and the movement of the towed array sensors. In both cases, the task is achieved by enhancing the amount of information collected by the towed array sensors.

Section 2 deals with the proposed method where the expressions related to the raw form of the proposed method, the optimal choice of the positioning of the towed array sensors, the optimal movement of the towed array sensors to enhance the performance of the proposed method are discussed. Mathematical modelling of the tracking problem, parameters to compare the various estimators is presented in Section 3. The discussion of the simulation results is done in Section 4 and finally the paper is concluded in Section 5.

2 Proposed method

2.1 Proposed estimate refining technique

The proposed refining method works on the principle of fusing the estimates which are given by the conventional estimators. The conventional estimators run with the help of the bearing measurements provided by the towed array sensors. The pictorial representation is presented in Figure 1. The estimator part of Figure 1 can be any of the nonlinear filter; however, in the paper the unscented Kalman filter is used. Here, the black box of the UKF is only presented in Figure 2 to keep our focus only on the refining method proposed and to avoid deviation from the main stream. The technique is expected to work well because here we are not depending on the measurement given by a single estimator but we are depending on the combination of the outputs given by a group of estimators. Secondly here, we are not depending on the measurements given by a single sensor; here we are depending on the measurements given by different combination of sensors. This proposed algorithm can also be applied to the active target tracking as in [25].

If the outputs of individual nonlinear estimators (estimates and covariances) are denoted by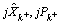with j=1, 2, 3, …, p, here, the expressions related to the nonlinear estimators (UKF) are not included to keep attention on the proposed method. However, the expressions are available in Ref. [2]. The fused estimate and covariance 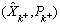can be obtained from any stochastic refiner like the LSE algorithm. Here, the estimation is made in such a way that the mean square error is at the minimum valu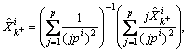e.where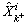is the ith element of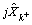andjpⁱ is the (i, i) element of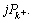

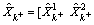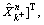
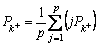…,  (1)

2.2 Higher order refining technique

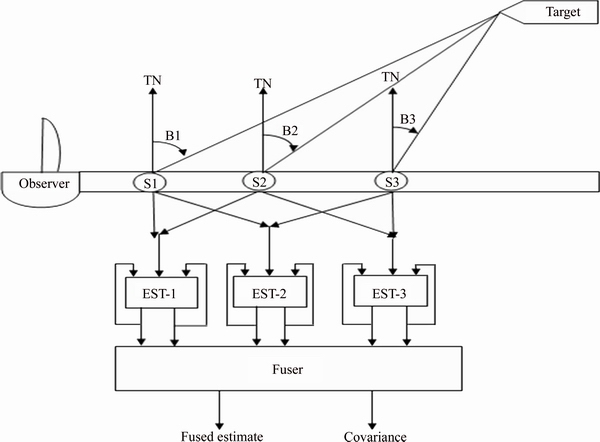
Figure 1 Proposed refining technique based estimator

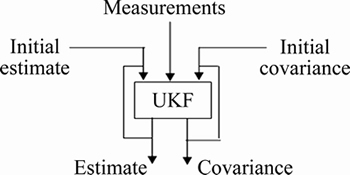
Figure 2 UKF black box

A higher order refining technique based estimator can be designed by increasing the number of intermediate nonlinear estimators whose outputs are to be fused. Here the number of sensors of TA should be increased but the number of inputs applied to each UKF remains the same, namely the dimension of the measurement matrix remains unchanged. The pictorial representation is shown in Figure 3. This is one way of doing that the alternate way of designing the higher order refining technique estimator is to keep the number of sensors as constant and to increase the number of inputs applied to each of the UKF, i.e., by increasing the dimensions of the measurement matrix. The block diagram of this approach is presented in Figure 4.

2.3 Optimal positioning of TA sensors

The performance of the proposed method can be improved by proper positioning of the Towed array (TA) sensors. Here we will see what should be the ideal positioning of the Towed array sensors in order to enhance the performance of the refining technique to the maximum extent. The Towed array can be placed in any of the positions like positions 1, 2, 3, 4, 5 as shown in Figure 5 below. If the TA is in position 1, then the bearing information collected by the three sensors is almost the same namely the angle made by the line of sight with respect to the true north at sensor 1 will be somewhere around 100°and same will be the angle observed at the other two sensors 2 and 3. This means that although we are using three different sensors but we are collecting very less information about the target. Now if we consider the TA in position 2, here the bearing information collected by the sensors in some what is different to the previous. So although we are using same three sensors and we are collecting more information about the target, the triangulation will be better and hence the tracking accuracy will be better. Now the question is what should be the ideal positioning of the TA sensors in order to enhance the performance of the proposed refining technique to the maximum extent. The answer to the question is that, the ideal positioning of the TA is the one at which the maximum information is collected by the sensors of the TA. This happens when the difference between the bearings collected by the three sensors is the maximum. And this happens when the triangulation is at maximum which in turn is possible when the angle between the LOS and the TA is at maximum. Or in simple words the TA should always be placed in such a position that the LOS appears to be the perpendicular bisector at the center sensor of the TA. Under these conditions the performance of the proposed refing algorithm will be at its best.

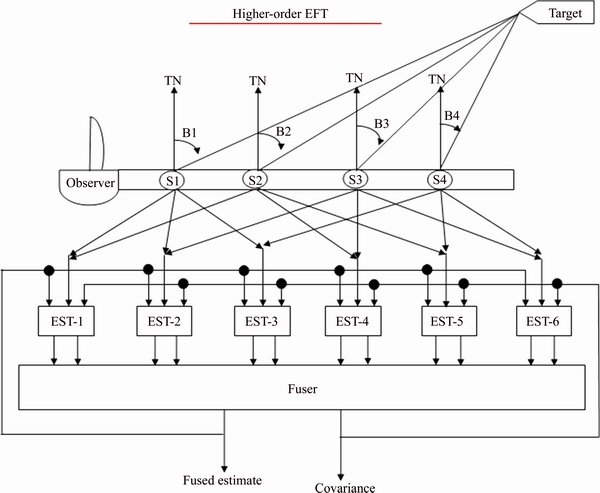
Figure 3 Higher-order refining technique

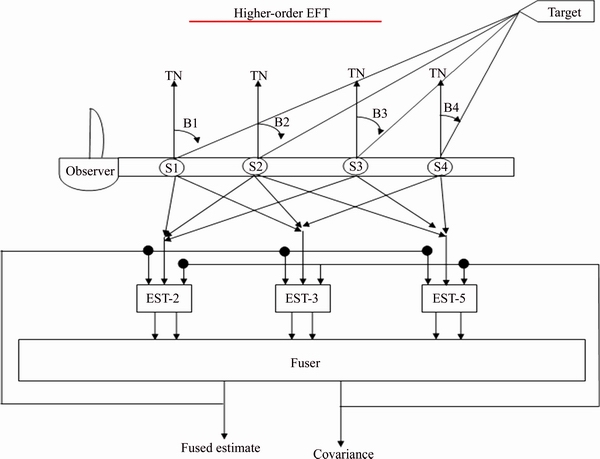
Figure 4 Higher-order refining technique (Alternate form)

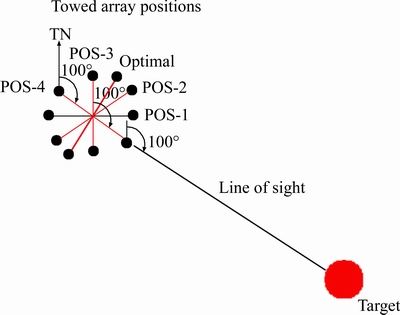
Figure 5 TA positioning options

2.4 Optimal movement of TA sensors

The superiority of the refing technique based algorithms improves when TA is made to move instead of remaining stationary at the place where it is. The movement cannot be a manoeuvering one because of the structure possesed by TA. The available options are to move away/towards/ stationary from the target. The best path is to travel in the enemy’s direction. There are two main resons for this peculier behaviour. One of them is explained with the help of Figure 6 given above. It can be noted that for same values of the bearing errors the range corruption is different for different target ranges. That is if the range is high, then the range corruption is high and vise versa. So when the ownship tries to head towards the target, the range and hence range corruption reduce. The other reason is, if the ownship moves in such a way to reduce the range (Figure 7), the difference between the azimuths at the sensors increases which causes more information collection and hence superior performance. The suggestive movement to yield better performance of the EFM algorithms is to move in the minimizing range direction.

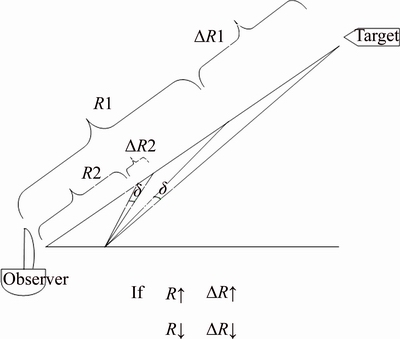
Figure 6 Geometry supporting lower ranges

3 Mathematical modelling

3.1 Mathematical modelling of moving torpedo

The state vector (t_X) for the moving torpedo tracking problem is commonly made of the position tx, ty and velocity elements t_vx, t_vy as 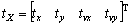and the state equation for a situation is in the form as follows

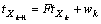                         (2)

where k is time instant. 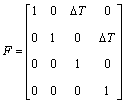and w_k represents the process noise with covariance matrix Q.and q is sigma of the acceleration errors.

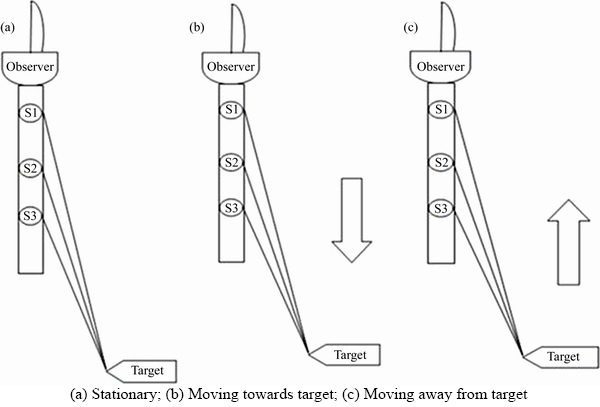
Figure 7 TA movement options:

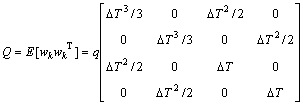 (3)

3.2 TA measurement modelling

The azimuth reading at the two sensors (s_ix, s_iy) and (s_jx, s_jy) denoted by (B_mik, B_mjk) makes the measurement vector t_Yk. The measurement equation can now be written as

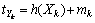                          (4)

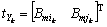
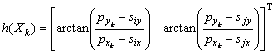
where 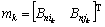is the measurement error matrix with a mean and covariance matrix 0, R.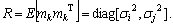 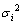and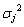are noise variances.

3.3 Performance comparison aspects

3.3.1 RMS Pos. Err.

It is the average distance between the estimated and the true position of the target.

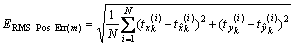 (5)

3.3.2 Average Pos. Err.

It is the ensemble mean of the root mean squares position error as obtained in RMS Pos. Err.

3.3.3 Convergence time

T_cm and T_c are the estimator’s times to pull the RMS Pos Err to <7% and <400 m of range.

4 Simulation results

4.1 Simulation parameters

Underwater scenario considered for testing the refining technique is given in Table 1.

4.2 Results supporting usage of estimate refining technique

For the underwater target tracking scenario as shown in part 1 of section 4 the refining technique along with algorithms (EFT-EKF/UKF) is applied and the following results are obtained.

It is observed from Figure 8 and Table 2 that the performance of the nonlinear algorithms like EKF and UKF is improved by incorporating the proposed refining technique (REF-EKF/UKF) along with them.

Table 1 Underwater scenario considered for tracking

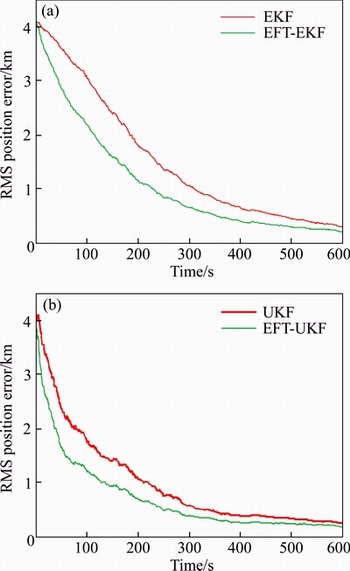
Figure 8 RMS Pos. Err. with (a) and without (b) refining technique

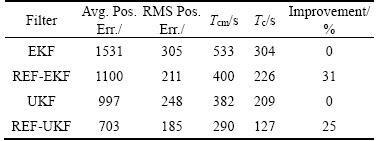
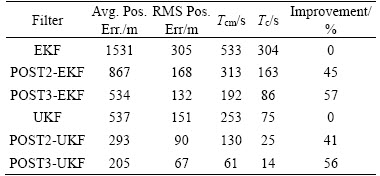
The RMS Pos. Err./Avg Pos. Err. of the proposed refining technique based conventional estimators like the EFT-UKF or REF-UKF is found to be 186 m/704 m which is much less than 249 m/998 m obtained by using traditional UKF. The same is the case observed with EKF where the numbers are reduced from 212 m/1101 m to 306 m/1532 m. The convergence times T_c/T_cm when UKF dealing with the proposed method (128 s/291 s) is observed to be far low compared to the values (210 s/383 s) obtained without application of the novel method. Similarly, the improvements are 25% and 30% when estimate refining technique is applied to the EKF and UKF respectively. All these improvements are achieved because of making a decision about the state of a moving target with the help of number of estimators instead of a single estimator.

Table 2 Comparision of non-linear estimators with and without refining technique

4.3 Results supporting usage of higher-order estimate refining technique

For the underwater target tracking scenario as shown in part 1 of section 4 both the higher-order and the lower-order refining technique based algorithms (Post2/3 EKF/UKF) are applied and the following results are obtained.

It is observed from Figure 9 and Table 3 that the higher-order refining technique based algorithms exhibit superior performance. The RMS position error, average position error convergence times T_c, T_cm are less for the third-order refining technique based algorithms compared to the second order which in turn is much less compared to the non refining technique based algorithms. Added to this, the improvement achieved by using the refining technique is approximately 40% and 55% when dealing with the second- and third-order refining mechanism based algorithms. The reason for exhibiting this superiority is that the estimate extraction from a larger number of sensors and the larger number of the intermediate estimators is obviously going to be much better than their lower number counterparts.

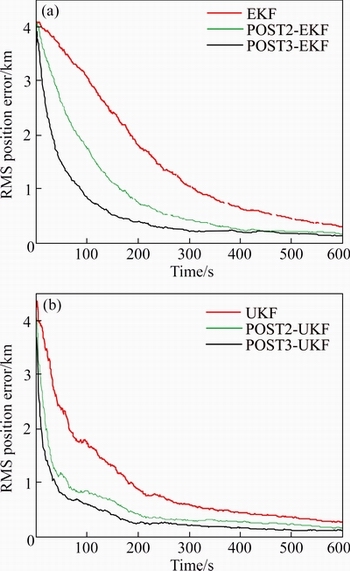
Figure 9 RMS position error for higher and lower-order refining techniques

Table 3 Comparision of non-linear estimators with different orders of refining technique

4.4 Optimal positioning of TA to enhance performance of proposed method

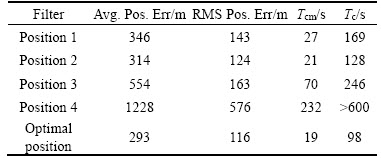
The refining technique based algorithms are applied to track a target for the same scenario as mentioned above but the positions of the TA are varied as in Figure 5 and the performance is accessed. The graphs in Figure 10 and Table 4 show that the performance of the refining technique is indeed at its best when the angle between the LOS and the TA is the maximum. The graphs clearly show that if the difference between the bearing measurements is low as in the case of 4 then the information collected by the sensors is the least, so the triangulation is very poor and hence the estimation error is very high, 577 m; on the other hand if the difference between the bearing measurements is high as in the case of 5 (optimal case) then the information collected by the sensors is high, so the maximum triangulation is possible and hence the estimation errors are very low, 117 m. The results certainly suggest that the TA should always be placed in a position where the difference between the bearings collected by the different sensors is at the maximum and which is possible only when the TA and LOS are the maximum or 90^o.

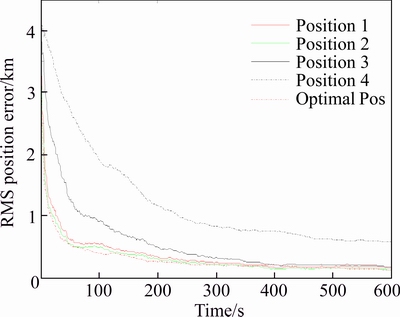
Figure 10 RMS position error when TA is at different positions

Table 4 Refining technique behaviour when TA is at various positions

4.5 Optimal movement of TA to enhance performance of proposed method

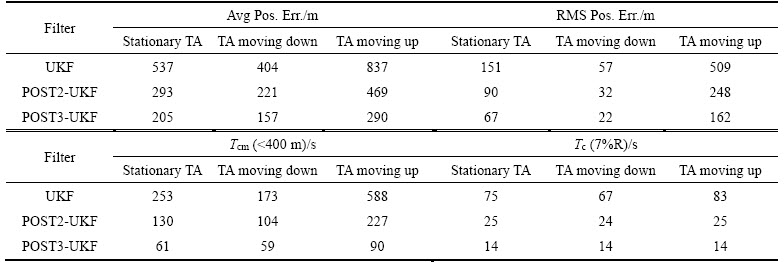
To justify the statement that the performance of the EFM is the best when the TA moves in the enemy’s direction, the target which is heading as in the case given in Table 1 is made to track with the same refining technique based UKF in three different cases. The first one is when the ownship is in a lazy condition or stationary; second and third cases are when the ownship moves towards and away from the enemy. The errors in the range obtained in different cases are shown in Figure 11. The quantitative comparison is shown in Table 5. The errors in the range are minimum (22 m) when the 3-order refining technique tracks the target by moving the TA in the enemy’s direction and maximum (162 m) when the same algorithm tracks the same target when the TA moves away. The same pattern is obeyed by all algorithms that indeed the suggestive way to enhance the performance of the EFM is to keep TA moving towards the enemy.

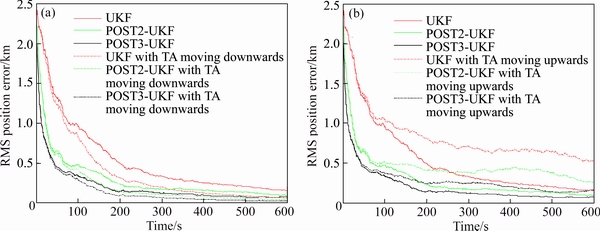
Figure 11 RMS position error when TA is moving in different directions

Table 5 Comparison of performance of refining technique when TA is moved in different directions

This superiority is due to the fact that when we are moving in the direction of the target, the difference between the bearings indeed increases, which in turn causes the sensors of TA to collect more information about the dynamics of a moving target. As a result of this, triangulation improves and hence the estimation errors are reduced to a great deal.

5 Conclusions

It can be concluded that the proposed refining technique when integrated with the available estimators produces excellent results when tracking targets in underwater scenarios. The higher-order versions of the refining technique produce better results. The performance of the novel technique reaches its best by proper positioning and movement of TA sensors. The optimal positioning of the TA is the one at which the LOS acts as a perpendicular bisector to the TA and the optimal movement is the one in which the range reduces. So finally we can conclude that a combination of proper positioning/movement of TA sensors and usage of higher-order refining technique can produce amazing results for bearings-only tracking issue.

References

[1] RAVI KUMAR D V A N, KOTESWARA RAO S, PADMA RAJU K. A novel stochastic estimator using pre-processing technique for long range target tracking in heavy noise environment [J]. Optik, 2016, 127(10): 4520–4530. DOI: https://doi.org/10.1016/j.ijleo.2016.01.196.

[2] RAVI KUMAR D V A N, KOTESWARA RAO S, PADMA RAJU K. Integrated unscented Kalman filter for underwater passive target tracking with towed array measurements [J]. Optik, 2016, 127(5): 2840–2847. DOI: https://doi.org/10. 1016/j.ijleo.2015.11.217.

[3] VIJAYA A, KOTESWARA RAO S, JAWAHAR A, KAR ISHMA B. Application of parameterized modified gain bearings-only extended Kalman filter for undersea tracking [J]. Indian Journal of Science and Technology, 2016, 9(13). 81630. DOI: http://dx.doi.org/10.17485/ijst%2F2016%2Fv 9i13%2F.

[4] RAVI KUMAR D V A N, KOTESWARA RAO S, PADMA RAJU K. Underwater bearings-only passive target tracking using estimate fusion technique [J]. Advances in Military Technology, 2015, 10(2): 31–44. DOI: http://aimt.unob.cz/ articles/15_02/04.kumar.pdf.

[5] DEOK J L. Nonlinear estimation and multiple sensor fusion using unscented information filtering [J]. Signal Processing Letters IEEE, 2008, 15: 861–864. DOI: https://doi.org/ 10.1109/LSP.2008.2005447.

[6] KALMAN R. A new approach to linear filtering and prediction problems [J]. Journal of Basic Engineering, 1960, 82(1): 35–45. DOI: https://doi.org/10.1115/1.3662552.

[7] SONG T, SPEYER J. A stochastic analysis of a modified gain extended Kalman filter with applications to estimation with bearings only measurements [J]. IEEE Trans Autom Control, 1985, 30(10): 940–949. DOI: https://doi.org/10. 1109/TAC.1985.1103821.

[8] JULIER S, UHLMANN J. Unscented filtering and nonlinear estimation [J]. Proc IEEE, 2004, 92(3): 401–422. DOI: https://doi.org/10.1109/JPROC.2003.823141.

[9] LIU K Z, LI J, GUO W, ZHU P Q, WANG X H. Navigation system of a class of underwater vehicle based on adaptive unscented Kalman fiter algorithm [J]. Journal of Central South University, 2014, 21: 550–557. DOI: https:// doi.org/10.1007/s11771-014-1973-9.

[10] ORTON M, MARRS A. Particle filters for tracking with out-of-sequence measurements [J]. IEEE Transactions on Aerosp Electron Syst, 2005, 41(2): 693–702. DOI: https://doi.org/ 10.1109/TAES.2005.1468758.

[11] CLOSAS P, BUGALLO M F. Improving accuracy by iterated multiple particle filtering [J]. Signal Processing Letters IEEE, 2012, 19(8): 531–534. DOI: https://doi.org/10. 1109/LSP.2012.2205565.

[12] FERNANDEZ G. Track-before-detect labeled multi- bernoulli particle filter with label switching [J]. IEEE Transactions on Automatic Control, 2016, 52(5): 2123–2138. DOI: https://doi.org/10.1109/TAES.2016.150343.

[13] YU Y J, COATES M J, RABBAT M G, BLOUIN S A. Distributed particle filter for Bearings-only tracking on spherical surfaces [J]. Signal Processing Letters, IEEE, 2016, 23(3): 326–330. DOI: https://doi.org/10.1109/LSP. 2016.2518173.

[14] BEARD M, BA-TUONG V, BA-NGU V. Multitarget filtering with unknown clutter density using a bootstrap GMCPHD filter [J]. Signal Processing Letters, IEEE, 2013, 20(4): 323–326. DOI: https://doi.org/10.1109/LSP.2013. 2244594.

[15] WANG S, FENG J, TSE C K. Spherical simplex-radial cubature Kalman filter [J]. Signal Processing Letters IEEE, 2013, 21(1): 43–46. DOI: https://doi.org/10.1109/LSP. 2013.2290381.

[16] ARASARATNAM I, HAYKIN S. Cubature Kalman filters [J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254–1269. DOI: https://doi.org/10.1109/TAC.2009.20198 00.

[17] WU H, CHEN S X, YANG B F, LUO X. Robust range-parameterized cubature Kalman filter for bearings-only tracking [J]. Journal of Central South University, 2016, 23(6): 1399–1405. DOI: https://doi.org/ 10.1007/s11771- 016-3192-z.

[18] ARASARATNAM I, HAYKIN S, ELLIOTT R J. Discrete-time nonlinear filtering algorithms using gauss-hermite quadrature [J]. Proceedings of the IEEE, 2007, 95(5): 953–977. DOI: https://doi.org/10.1109/JPROC.2007. 894705.

[19] GODAVARI T, UMADEVI J. Cloud computing based real-time vehicle tracking and speed monitoring system [J]. International Journal of Control Theory and Applications, 2016, 9(4): 1823–1830. DOI: http://www.serialsjournals. com/articles.php?volumesno_id=1037&journals_id=268&volumes_id=848

[20] DWIVEDI P, BHALE P, BHATTACHARYYA A, PADHI R. Generalized estimation and predictive guidance for evasive targets [J]. IEEE Transactions on Automatic control, 2016, 52(5): 2111–2122. DOI: https://doi.org/10.1109/TAES. 2016.140861.

[21] KANT K, BATIA V, RJORA V. A novel robot navigation technique based on signal strength [J]. International journal of Control Theory and Applications, 2016, 9(41): 227–236. DOI: http://www.serialsjournals.com/articles.php?volumesno _id=1153&journals_id=268&volumes_id=848.

[22] VERMA S, SINGH C, MITTAL S, ARORA P, REHALIA A. Mobile surveillance spheroid robot with static equilibrium camera, leaping mechanism and KLT algorithm based Detection with tracking [J]. International Journal of Control Theory and Applications, 2016, 9(41): 473–488. DOI: http://www.serialsjournals.com/articles.php?volumesno_id=1153&journals_id=268&volumes_id=848.

[23] KARTHIKEYAN R, KAVIDA C. Motion tracking and segmentation in the compressed domain using spatio temporal Markov random fields [J]. International Journal of Control Theory and Applications, 2017, 10(1): 73–77. DOI: http://www.serialsjournals.com/articles.php?volumesno_id=1154&journals_id=268&volumes_id=1065.

[24] JIAN L, LI X R. Tracking of extended object or target group using random matrix: new model and approach [J]. IEEE Transactions of Aerosp Electron Syst, 2016, 52(6): 2973– 2989. DOI: https://doi.org/10.1109/TAES.2016.130346.

[25] RAVI KUMAR D V A N, KOTESWARA RAO S, PADMA RAJU K. Under water active target tracking using kalman filter [J]. International Journal of Engineering Research and Technology, 2013, 2(10): 3982–3988. DOI: https://www.ijert. org/browse/volume-2-2013/october-2013-edition?start=580.

(Edited by DENG LU-xiang)

中文导读

海底环境下一个新的鱼雷跟踪问题的估计算法

摘要：本文介绍了一种新的估计算法，用于处理较为普遍的海底问题，即鱼雷跟踪问题。该方法仅使用角度测量，与现有滤波器相比效果更好。借助简单的噪声优化法（如最大似然滤波法或其他相类似的算法），新算法通过传统非线性方法产生的输出结果产生更好的估计值。引入的方法可以两种方式扩展到更高版本。第一种方法通过增强中间滤波器的计数来提取更好的估计值和协方差，第二种方法则是接受更多的输入以便在不增强中间滤波器计数的情况下获得性能的改进。进一步提取拖曳阵列传感器位置以改善算法性能的方法是将瞄准线和拖曳阵列相垂直。通过将所有权转移到减少范围的方向，结果可以变得更好。所有结果均在MATLAB中验证。

关键词：估计算法；鱼雷跟踪；仅使用角度测量；瞄准线；最大似然滤波器

Received date: 2017-05-28; Accepted date: 2018-11-10

Corresponding author: D. V. A. N. RAVI KUMAR, Assistant Professor; Tel: +918985482118; E-mail: ravikumardwarapu@ gvpcew.ac.in; ORCID: 0000-0003-2586-5337