一种改进的基于活动轮廓和光流的运动目标分割方法

方宇强，戴斌，宋金泽，单恩忠

(国防科学技术大学 机电工程与自动化学院，湖南 长沙，410073)

摘要：将光流技术和几何活动轮廓模型结合起来对运动目标进行分割，一方面可以通过算法分割出运动目标轮廓，另一方面，使得算法面对背景变化的情况仍具有一定的适应性。为了更好地将二者结合起来，进行2个方面的改进：建立基于运动边缘的几何活动轮廓模型，从而克服光流计算中由弱纹理区域产生的运动空洞对分割的影响；引入边缘增强的非线性扩散作为光流计算模型中的平滑项约束，可以在平滑流场的同时减小运动边缘处平滑效果而保护边缘，进而提高运动目标分割的完整性。研究结果表明：与现有算法相比较，该算法能够更准确地分割出运动目标的轮廓，同时在一定程度上克服背景运动的情况。

关键词：光流；活动轮廓模型；非线性扩散；运动目标分割

中图分类号：TP391          文献标志码：A         文章编号：1672-7207(2011)04-1035-08

An improved moving objects segmentation method based on optical flow technique and active contour model

FANG Yu-qiang, DAI Bin, SONG Jin-ze, SHAN En-zhong

(College of Mechatronic Engineering and Automation, National University of Defense Technology,

 Changsha 410073, China)

Abstract: Combining the optical flow technique and geometric active contour model to segment moving objects is a promising method. It not only can segment the contour of target accurately but also can be extended to the case with dynamic background. In order to combined these two techniques more effectively, two sides were improved: A new active contour model, which was based on motion edges, was proposed, so the impacts from low textured motion areas can be eliminated; reducing smoothing at those locations where edges in the flow field occur during the computation, the edge-enhancement nonlinear diffusion constraint was chosen as a smoothness term in optical flow computation. Then the flow field could preserve the motion discontinuities which were important information to segmentation, so a better segmentation result could be gotten. The experimental results show that this algorithm performs well, even in the situation of dynamic background. Compared with other methods, more accurate results can be gotten by this method.

Key words: optical flow; active contour model; nonlinear diffusion; moving objects segmentation

运动目标的分割就是在给定的图像序列中提取出感兴趣的运动区域，它可以作为重要步骤应用于各项计算机视觉任务中，如智能监控系统、军事侦察、图像压缩、人的运动分析等。同时，人类的视觉往往对运动的物体或目标感兴趣，大量有意义的视觉信息都包含在运动中。但在实际的图像采集过程中，光照、相机运动、阴影等因素都会给运动目标的分割带来很大的困难；所以，运动目标的分割是计算机视觉领域极具意义且具有挑战性的课题之一。光流技术作为一种重要的二维运动估计技术，能够很好地反映出图像中的运动变化，为运动目标的分割提供有效的信息。如Polley等^[1-2]利用对光流场的估计来检测运动目标。而光流技术与其他常用的运动检测技术，如背景建模、帧间差分法等相比，一方面能够在进行运动检测的同时，给出运动的大小和方向信息；另一方面，对于场景运动的情况具有较好的鲁棒性，即当摄像机运动的情况下，依旧能够有效地反映出运动不一致的区域，如Giachetti等^[2-3]将光流技术应用于智能车辆的障碍物检测中。总之，有效地计算出光流场可以为运动目标的分割提供必要信息。活动轮廓模型是被广泛关注的图像分割方法，主要分为参数活动轮廓模型和几何活动轮廓模型。其中几何活动轮廓模型由于采用了水平集的方法而具有较强的拓扑自适应性，能够很好地处理目标的分裂与合并，所以，得到了广泛应用，如Muford等^[4]提出的M-S模型可以同时实现对图像的分割和去噪，Chan等^[5]于区域分割的思想提出了经典的C-V模型。这些模型一般依据目标的纹理、颜色、边缘等信息建立能量泛函，然后，通过最小化这一能量泛函，得到曲线的演化驱动函数，使曲线收敛于目标轮廓，实现目标的分割。近年来，活动轮廓模型逐渐地被应用于运动目标分割中。其基本思想是将运动信息融入到所要建立的能量泛函中，从而有效地将运动目标分割出来。如万成凯等^[6]通过在能量函数中引入Gauss混合背景模型，来实现运动目标的分割，并取得了很好的效果。 然而，混合Gauss背景建模方法虽然可以有效地处理复杂场景下的目标检测，但无法有效地克服摄像机移动的情况，使其应用范围受到约束。由于光流技术不易受摄像机运动的影响，所以，结合光流和活动轮廓模型的运动目标检测技术受到关注，如Polley等^{[1, 7]}将光流信息融入到活动轮廓模型中进行运动目标分割。然而，其中仍存在以下问题：

一是活动轮廓模型的选择。当选用光流信息作为运动目标分割的依据时，应充分考虑目标的光流特征，运动目标往往在其边界处有较强的光流值，而其内部由于特征一致性较高，常常产生较弱的光流甚至“运动空洞”。所以，选择基于区域的分割模型并不合适，分割时应该更多的考虑运动边缘信息。

二是光流的计算方法。如文献[1, 7]中的计算模型，平滑项约束都采用的是线性平滑，这样，就在平滑整个光流场的同时，使运动边界模糊化，衰减了重要的分割信息——目标的边缘运动信息，降低了分割的准确性。

针对上述问题，本文作者提出一种改进的基于活动轮廓和光流的运动目标分割方法。该方法采用基于非线性扩散的光流计算模型，能够有效地保留运动目标的边缘运动信息，并将光流信息有效地融合到基于边缘的几何活动轮廓模型中，实现运动目标的分割。实验结果表明：本文作者采用的方法充分结合了光流和几何活动轮廓模型的特点，相比于以往的算法，取得了较高的分割准确性。

1  基于非线性扩散的光流估计

1.1  扩散-反应式光流计算模型

扩散是物理学中的1个常见的概念，表示某种浓度分布不均匀的杂质在某种介质中的迁移。若以函数φ(x, y, z, t)表示浓度随时间t和空间(x, y, z)的变化，空间分布的不均匀性用梯度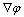来刻画，那么，扩散过程可表述为：

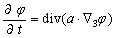
其中：a为传导系数。

经典的光流计算方法中，一般首先建立相应的光流计算模型即能量泛函如Horn-Schunck全局平滑约束模型^[8]以及Bruhn等^[9]提出的结合全局和局部平滑的约束模型，然后，通过变分法来实现能量泛函的最小化，从而得到相应的光流解，并取得了较好的光流计算结果。而能量泛函的设计中一般包括了满足相容性约束的数据项和满足光滑性约束的正则项，如下式(Horn-Schunck全局平滑约束模型^[8])：

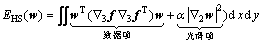   (1)

式中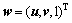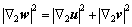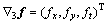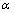：；；；为正则化参数；f为图像中的像素点；w为此点的光流。则由变分法，可以得到式(1)取得最小值时的欧拉方程，并采用梯度下降流方法表示为：

则方程组可以简写为如下形式：

    (2)

因而，光流计算就可以描述为如式(2)所示的反应扩散过程。将光流的求解过程视为一个从无序到有序，从不稳定到稳定的流场反应扩散过程。其中，反应项保证了光流由非稳态到稳态过程中满足自身的运动模型，而扩散项可以控制光流的平滑程度和平滑方向。

1.2  基于非线性扩散光流计算模型

从式(2)可以看出：在经典的光流计算模型中，传导系数a都为常数1，即一种线性扩散的过程。线性扩散在进行流场平滑性约束的同时会造成运动边缘信息的模糊化。而运动边缘信息是光流场的重要信息，同时也是运动分割的最重要特征。所以，为了在进行平滑性约束的同时保护边缘，应使传导系数依赖流场的局部信息变化，实现非线性扩散。如Nagel等^[10-11]采用有向平滑的方式来提高光流计算的精度。本文也是基于这种想法，为了提高后期分割的准确性采取了一种非线性扩散的光流计算方法。

由Perona和Malik^[12]提出的P-M方程是应用于图像滤波的偏微分方程，利用图像的梯度模值，进行各向同性的非线性扩散，将图像的滤波过程与图像边缘检测的过程结合起来。由于数学上P-M模型解的存在唯一性不能保证，Cattle等^[13]针对这一病态性，给出了其空域正则化模型：

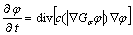
其中：c为满足一定约束的单调减函数，称为扩散率函数。设扩散函数为：

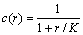
该函数可以保证当r ＜＜  K即梯度模值较小时，扩散过程在边缘的切向和法向都是正扩散，能够起到平滑作用，而当r＞K时，在边缘的切向上是正扩     散，而在法向上是反扩散，锐化边缘。本文利用非线性扩散的想法改进原有的线性扩散过程，设置相应的扩散函数，将正则化的P-M方程引入到光流计算   中，得到同时具有平滑性约束和运动边缘增强的光流计算模型：

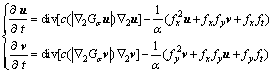 (3)

1.3  数值计算

对于式(3)，本文采用半隐式的计算方案，离散  化为：

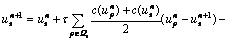
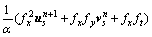
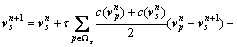
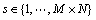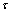其中：扩散项的散度算子采用“半点”离散化方案，如图1所示，式中下标；为离散化时所用的四邻域范围；为时间步长。

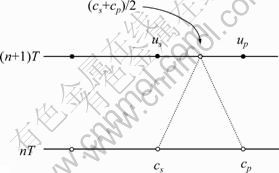
图1  半点离散化方案

Fig.1  Half-point discretisation

若将符合图像大小(M×N)的流场数据u和v转换成M维、N列向量，则可将离散化的公式转化为：

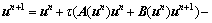
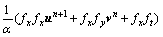
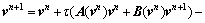
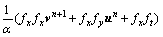
其中：矩阵和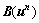表示MN×MN的稀疏化系数矩阵，其中元素表示为

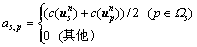
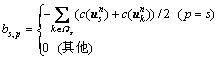
这样，光流的求解可以进一步转化为解下述非线性方程组：

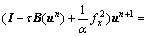
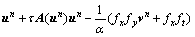
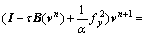
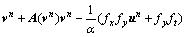
可以看出，方程中的系数项中和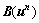会随着每次计算的结果实时改变，而为了克服这种非线性情况，可以采用Lagged-Diffusivity方法^[14]将非线性等式求解分解为一系列的线性方程组求解。具体步骤如下：

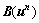(1) 由第n层数据计算权系数和的 数值。

(2) 在固定系数情况下，采取线性方程组的迭代解法(如Gauss-Sidel方法)进行求解，计算出下一时刻的光流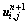和。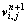

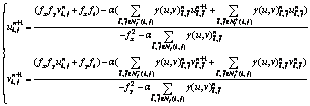
 (3) 再根据新计算出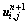和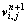，若2层数值差小于设定精度阈值则结束，否则回到第1步，重新计算权系数，求解线性方程组。

这样，便可以通过非线性扩散来改进光流计算中的平滑过程，保留运动的不连续区域，为后期的运动分割提供更为准确的分割信息。

2  基于运动边缘信息的活动轮廓模型

基于水平集方法和曲线演化理论的几何活动轮廓模型中，曲线运动方程往往来自于最小化闭合曲线C的某一能量泛函。如基于边缘信息的测地线活动轮廓模型(GAC)、基于区域信息的Chan-Vese模型等。针对这类由曲线的能量泛函最小化所导出的曲线演化问题，常采用变分方法进行求解。常见的模型往往针对单幅图像中的边缘、亮度和纹理等空间域信息，而运动目标本身就具备不同的纹理和亮度区域，仅仅考虑空域信息往往很难将目标完整地分割出来。但若将光流信息引入模型，则可以很好地反映图像在时域中的变化，有效地分割运动区域。

运动目标往往在其边缘处产生较强的光流信息，而其内部光流信息较弱，甚至产生“运动空洞”，也就是说，运动边缘信息与区域信息相比更有利于分割。本文在得到合适的光流场后，进一步建立基于运动边缘信息的几何活动轮廓模型，实现运动目标的分割。

封闭曲线C可以用如下的隐式表达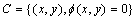：。式中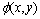：是曲线C的嵌入函数，常初始化为符号距离函数，故曲线C为函数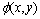的零水平集。

假设得到的光流为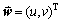，而运动边缘的光流模值往往较大，所以，可以将光流的模值信息融合到活动轮廓模型中，具体描述如下：

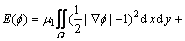
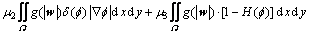
  其中：，。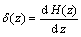

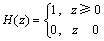边缘停止函数描述为：。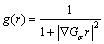

而上式中第1项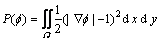的加

入在于避免重新初始化的问题，最小化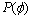则要求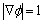，即要求嵌入函数在演化的过程中尽可能地保持为距离函数，这样，模型本身就具有了保持距离函数的能力，简化了重初始化的工作^[15]；第2项和第3项分别是驱动曲线停止于边缘的“内力”和“外力”。参数μ₁，μ₂和μ₃用于控制各项作用的相对大小。

引入时间辅助变量t和正则化的Heaviside阶跃函数，可以求出能量泛函对应的梯度下降流：

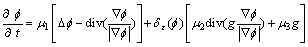  (4)

，

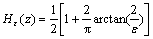对于如上的偏微分方程，本文采用显式的计算方案，即

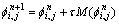
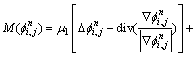
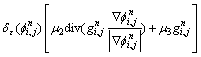
其中，散度计算仍采用半点离散化格式：

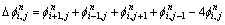
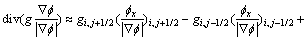
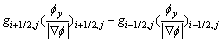
式中每一项“半点”值用相邻2个“整点”的平均值近似表示，如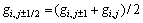：。这样通过选取合适的时间步长，经过有限步迭代可以得到最终解。

3  实验结果与分析

实验1  用基于非线性扩散的光流计算方法和传统的基于线性扩散的光流方法比较。实验图像采用Traffic视频的连续2帧，大小为688×565的灰度图像，程序实现采用Matlab7.1仿真软件。在实验中，分别采用本文的光流算法和传统的光流算法得到相应的光流场，并为了直观显示，采用HSV模型来表示光流的大小和方向，如图2所示。从图2可以看出：本文方法相比于传统方法，可以得到准确的光流场；而从图中局部放大区域的光流场来看，本文算法由于改进了光流计算模型中的扩散项，采取了非线性扩散的方式，所以，减小了运动边缘处的平滑效果，保留了更为准确的运动区域边缘信息。

实验2  将本文算法与结合光流和基于区域的活动轮廓模型分割算法相比较，验证本文算法的有效性。实验素材采用实拍视频，图像为320×240的彩色图像，描述固定场景下多目标的运动情况，如图3所示。图3中列出视频中2组典型的图像序列，并分别利用本文算法和基于区域的算法进行运动目标的分割。从分割结果看，基于区域的方法受到“运动空洞”的影响，往往不能完整地分割出运动目标的轮廓；而本文方法很好地利用了光流计算产生的强边缘信息，并有效地将其融合到基于边缘的几何活动轮廓模型中，较完整地分割出运动的目标，同时也说明水平集方法具备拓扑适应性。

图2  光流计算效果对比实验

Fig.2  comparison of optical flow fields

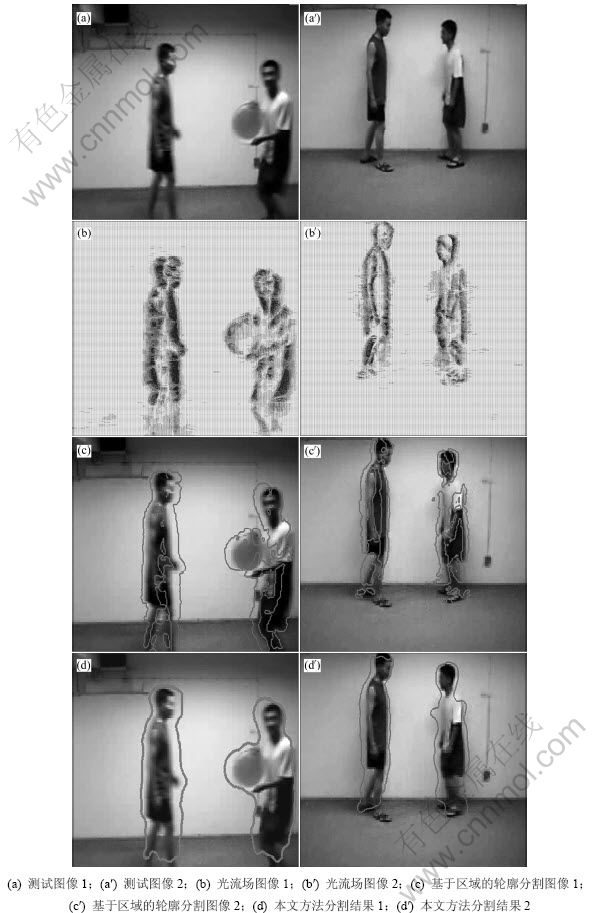
图3  轮廓分割效果对比

Fig.3  Comparison of different segmentation results

图4  运动场景的分割

Fig.4  Segmentation results with dynamic background

实验3  为了更好地说明本文算法对摄像机运动情况的适应性，采用一段车载摄像机录制的视频进行实验。视频图像为640×480的彩色图像，描述了不同时刻车辆行驶在校园道路上的情况。利用本文算法，分割出场景中相对运动的行人目标。其中分割区域根据实际的道路情况来确定，规定为车前方的一块梯形区域，如图4所示。而场景中的运动目标产生的光流往往与车辆本身行驶时产生的光流场不同，利用这种相异性可以使轮廓曲线收敛于道路区域中相对运动明显的边缘区域。从实验结果看，本文算法具备了分割出动态场景中相对运动目标的能力。然而，真正应用于移动机器人的环境感知中还有很多因素需要考虑，如道路上的水迹、阴影的影响等，但在相对简单的场景下，本文算法具有一定的有效性，体现了算法的应用和发展前景。

4  结论

提出了一种改进的基于活动轮廓和光流的运动目标分割算法，在以下方面进行了较好的改进。

(1) 该算法改进了传统光流算法中的扩散约束，采取了边缘增强的非线性扩散约束，有效地保护了运动目标的运动边缘，得到了更为准确的运动边缘，可以为后期分割提供更有效、更完整的信息，使得基于光流技术的运动目标分割算法更加准确和有效。

(2) 将光流信息融合到基于边缘的几何活动轮廓模型中，建立新的运动分割模型，并通过相应的数值计算方法，实现完整的运动目标分割。几组图像数据上的实验结果说明本文算法与以往的算法相比有所改进，得到了更为完整的运动目标轮廓，用运动边缘信息代替运动区域信息，使活动轮廓和光流信息结合模型更有效。

(3) 该算法面对摄像机运动的情况仍具有一定的适应性，可以分割出动态场景中的相对运动目标，充分体现了光流技术应用于运动分割中的优势和该算法广阔的应用前景。

参考文献：

[1] Polley R L, Max Q H M, Peter X L. Optical flow and active contour for moving object segmentation and detection in monocular robot[C]//IEEE Conference on Robotics and Automation. Orlando, Florida: IEEE Comput Soc, 2006: 4075-4080.

[2] Smith S M, Brady J M. ASSET-2: Real-time motion segmentation and shape tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(8): 814-820.

[3] Giachetti A, Campani M, Torre V. The use of optical flow for the autonomous navigation[J]. IEEE Transactions on Robotics and Automation, 1998, 14(1): 34-48.

[4] Muford D, Shan J. Optimal approximation by piecewise smooth functions and associated variational problems[J]. Communication Pure Apply of Mathematics, 1989, 42(4): 577-685.

[5] Chan T, Vese L. Active contours without edges[J]. IEEE Transaction on Image Processing, 2001, 10(2): 266-277.

[6] 万成凯, 袁宝宗, 苗振江. 一种基于活动轮廓和Gauss背景模型的固定摄像机运动目标分割算法[J]. 中国科学F辑: 信息科学, 2009, 39(4): 391-396.
WAN Cheng-kai, YUAN Bao-zong, MAO Zeng-jiang. A moving object segmentation algorithm for static camera via active contours and GMM[J]. Science in China Series F: Information Science, 2009, 39(4): 391-396.

[7] Zinbi Y, Chahir S. Moving object segmentation using optical flow with active contour model[C]//IEEE Conference on ICTTA. Damascus: IEEE Comput Soc, 2008: 273-276.

[8] Horn B K P, Schunck B G. Determining optical flow[J]. Artificial Intelligence, 1981, 17(1/3): 185-203.

[9] Bruhn A, Weickert J. Lucas-Kanade meets Horn-Schunck: Combining local and global optical flow methods[J]. International Journal of Computer Vision, 2005, 61(3): 211-231.

[10] Nagel H, Enkelmann W. An investigation of smoothness constraints for the estimation of displacement vector field from image sequence[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(5): 565-593.

[11] Weickert J, Schnorr C. A theoretical framework for convex regularizers in PDE-based computation of image motion[J]. International Journal of Computer Vision, 2001, 45(3): 245-264.

[12] Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639.

[13] Cattle F, Coll T, Lion P L. Image selective smoothing and edge detection by nonlinear diffusion[J]. SIAM Journal on Numerical Analysis, 1992, 29(1): 182-193.

[14] Chunming L, Chenyang X. Level set evolution without re-initialization: A new variational formulation[C]//IEEE conference on CVPR. San Diego, CA: IEEE Comput Soc, 2005: 430-436.

[15] Chan T, Mulet P. On the convergence of the Lagged diffusivity fixed point method in total varietion image restoration[J]. SLAM Journal on Numerical Analysis, 1999, 36(2): 354-367.

(编辑 陈爱华)

收稿日期：2010-06-10；修回日期：2010-08-15

基金项目：国家自然科学基金重点资助项目(90820302)

通信作者：宋金泽(1979-)，男，陕西西安人，博士研究生，从事模式识别与智能系统研究；电话：13574841568；E-mail: yqfang506@gmail.com