文章编号:1004-0609(2007)01-0085-07
分子动力学模拟金属玻璃压痕过程的应力晶化行为
王海龙,王秀喜,王 宇,梁海弋
(中国科学技术大学 中科院材料力学行为和设计重点实验室,合肥 230026)
摘 要:采用Mishin镶嵌原子势,通过分子动力学方法模拟金属玻璃在压痕过程中的晶化行为,从微观结构演化的角度考察应力晶化过程中晶粒的形核、长大与合并的过程。局部较大剪切应力导致内部临近的非晶原子形成晶核,发生晶粒生长与合并的区域与Hertz理论符合。最终生成的晶粒具有面心立方结构,其(111)方向平行于剪切面。计算结果与文献中的实验现象一致,并且符合最小能量准则。
关键词:金属玻璃;应力晶化;分子动力学;压痕
中图分类号:TG46.1; TB115 文献标识码:A
Molecular dynamics simulation of stress-induced crystallization behavior during indentation for metallic glass
WANG Hai-long, WANG Xiu-xi, WANG Yu, LIANG Hai-yi
(CAS Key Laboratory of Mechanical Behavior and Design of Materials,
University of Science and Technology of China, Hefei 230026, China)
Abstract: The stress-induced crystallization behavior was simulated during the indentation deformation process for metallic glass copper using molecular dynamics method. The Mishin embedded atom method (EAM) was adopted as the interaction among atoms in the system. The nucleation, growth and coalescence of crystal grains were investigated through the evolution of microstructure. The local shear stress of amorphous system makes neighboring atoms nucleate. The site of growth and coalescence of crystal grains agrees well with the Hertz theory. The final crystalline phase has a FCC structure and the (111) plane is parallel to the shear direction. The computational result is consistent with the reported experiment phenomena and the minimum energy principle.
Key words: metallic glass; stress-induced crystallization; molecular dynamics; indentation
金属玻璃材料具有高硬度、耐摩擦和低硬化等优异的力学性能,被广泛应用于宇航和工业制造领 域,是极具潜力的工程材料[1]。在弯曲和压痕实验 中,可以观察到在非晶剪切带内部存在纳米晶粒[2-3],但由于绝热剪切导致的局部温升,无法阐明应力晶化机制。Argon等[4]在室温下对非晶进行准静态加载的纳米压痕实验,排除了局部温度升高,发现压痕附近分布着应力导致的纳米晶粒,首次确认了应力晶化效 应。近年来,通过实验方法对金属玻璃的热力学性能展开大量的研究[5-6],对非晶进行退火或应力晶化成为制备纳米晶体材料的有效方法[7]。
金属玻璃的力学性能源于其独特的微观结构,而其微观结构又与合金的组分和冷却历史有关。然而微结构的演变机理很难由实验获得,计算机模拟技术成为获取这些信息的有效手段。近年来,人们用分子动力学(MD)方法成功地模拟了大量金属玻璃形成和塑性变形过程[8-11],并观察到剪切带中由应力导致的晶化现象 [10-11]。拉伸和剪切变形比较均匀,很难建立晶粒的形成演化与剪切应变之间的联系。本文作者通过分子动力学方法模拟非晶金属Cu在压痕变形过程中的晶化行为,从微观结构演化的角度考察和分析应力晶化过程中晶粒的形核、长大与合并过程,建立晶核生长以及晶粒方向与剪切应变之间的一般规律。
1 模拟方法与过程
1.1 原子势能函数
镶嵌原子势[12-14](Embedded atom method, EAM)是基于有效介质理论的半经验多体势函数,适合模拟金属及其合金原子间的相互作用,可表示为

Mishin等[12]结合第一原理的计算结果,采用更多的参数进行拟合,得到更高精度的势函数。其拟合参数包括金属Cu的结合能、弹性模量、表面能、堆垛层错能、热膨胀系数和压缩系数等多个热力学参数,并能精确地再现金属Cu的相变过程以及特征性质,包括热力学熔点[15]和玻璃转化温度[16]。由于Mishin镶嵌原子对金属Cu晶态、液态,特别是非晶态的热力学性质的精确描述,适合作为模拟应力晶化原子过程的势函数。
1.2 结构分析方法 1.2.1 径向分布函数
径向分布函数(RDF)[17] g(r)与衍射得到的干涉函数互为Fourier变换,是理论和实验对照的基本依据,也是描述液态和无序体系的基本函数。它反映了以一个粒子为中心,在半径 r ~ r+dr的空间范围内发现另一个粒子的概率,描述了一个原子与周围其它原子按距离分布情况。理想晶格结构,在不同近邻位置出现峰值,温度升高导致峰值减弱甚至消失,关键峰值的消失表明熔化开始。径向分布函数的定义为

1.2.2 公共近邻分析
公共近邻分析[18]采用指标I、J、K、L描述系统中局域团簇的结构特征。I表示原子对所属类型,近邻为1,非近邻为2;J为原子对近邻成键数;K表示这些近邻的原子中彼此成键的数目。对某些结构组态来说,仅用I、J、K还不能唯一标识,因此引入第四个参数L,用来区分拓扑结构。例如:1 661和1 441为体心立方的特征键对,1 551为正二十面体的特征键对,1 541和1 431为破损正二十面体的特征键对,1 421既为面心立方的特征键对,又与1 422一起成为密排六方的特征键对,是金属Cu原子体系结晶的标志。
1.2.3 原子Voronoi体积与应力
Voronoi体积这一概念早在1908年即被提出[19]。原子Voronoi元胞的边(面)是原子与其它节点连线的垂直平分线(面),这些垂直平分线(面)形成的最小闭包即为Voronoi元胞。Voronoi构型是对空间随机分布点进行区域划分的有效手段,Voronoi元胞划分具有唯一性,其体积等空间几何特征符合正态分布。
原子应力描述了一个原子与周围原子之间相互作用的强度,反应了一个原子的当前受力状态,量纲是能量密度。原子应力在1954年被第一次引入[20],广泛用于解释原子结构模型的数值模拟结果。在零温度下,第α个原子的应力可表示为

1.3 模拟基本过程
金属玻璃的生成过程: 三维周期边界条件下,液态Cu在2 000 K弛豫50 ps达到平衡状态,然后以1014 K/s的冷却速率降温到100 K。在100 K温度下弛豫50 ps,冷却到1 K。然后,X和Y方向保持周期边界条件,Z方向改为自由表面,在1 K下弛豫50 ps,得到1 K温度下的非晶态金属Cu薄膜。压力始终控制为零。动力学方程用Verlet算法的速度形式进行求解,时间步长取为1 fs,压痕过程采用位移控制方法。温度控制采用Nose-Hoover方法[21],压力控制采用Parrinello-Rahman方法[22]。
如图1所示,金属玻璃模型尺寸为29.1 nm×1.83 nm×21.8 nm,共有96 000个原子,X和Y方向保持周期边界条件,Z方向为自由表面。采用Mishin镶嵌原子势[12]模拟金属原子的相互作用,可用排斥势描述圆柱形压头与金属原子之间的作用[23],即
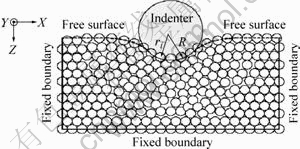
图1 金属玻璃的计算模型
Fig.1 Simulation model of metallic glass

压头半径R=6 nm,压入速度v=3 m/s,时间步长取为1 fs,温度控制在1 K。模拟实际对应圆柱压头Z方向加载厚度为21.8 nm的金属玻璃薄膜,薄膜处于平面应变状态。
2 模拟结果与分析
2.1 金属玻璃模型
图2所示为不同冷却率下形成的晶态和玻璃态金属Cu的径向分布函数。冷却速率为1012 K/s时形成金属晶体;冷却速率为1014 K/s时,形成金属玻璃。金属玻璃与液态金属相比,函数的峰值与宽度变化不大,仅第二峰发生分裂,这是非晶态金属玻璃Cu形成的标志。
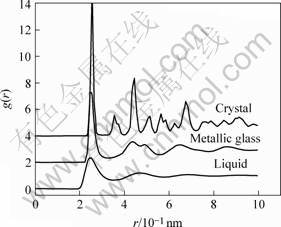
图2 金属玻璃和晶体的径向分布函数
Fig. 2 RDF of metallic glass and crystal
图3所示为金属玻璃原子能量统计分布图。金属玻璃Cu原子为正态对数分布,但离散度较大,接近常规的正态分布。这表明金属玻璃Cu原子能量分布混乱程度很高,局部位置原子能量差别很大。
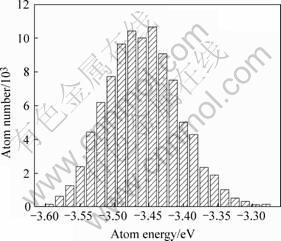
图3 原子内能统计分布图
Fig. 3 Distribution of atomic energy
图4(a)所示为中心层局部截面原子Voronoi体积分布图。金属玻璃内部存在着明显的局部膨胀和局部收缩现象,原子体积分布不均匀。金属玻璃原子体积分布的离散性较大,平均值为12.122(大于理想纳米多晶的11.810)。原子体积单位为10-3 nm3。

图4 截面原子体积(a)与静水压(b)等值线
Fig.4 Section isolines of atomic volume(a) and static pressure(b)
图4(b)所示为中心层截面原子静水压力等值线,样品内部压力不为零,存在着自平衡的本征应力。金属玻璃内部存在着明显的拉伸和压缩应力分布区域,原子应力分布不均匀,均方差达到4.466 GPa。金属玻璃的原子能量、原子Voronoi体积和原子应力分布的离散程度很高,变化十分剧烈,在金属玻璃中存在大量局部收缩和局部膨胀区域,导致剧烈变化的拉伸和压缩本征应力,非稳态结构特征将会对金属玻璃的力学性能产生影响。
2.2 微观结构演变
图5(a)所示为压痕深度达到1.5 nm时的原子构型图,在压头的右下方发现明显的晶化现象,由局部放大图5(b)可观察到生成晶粒的(111)方向与剪切方向平行。根据卢柯等[24-25]的切变合并或切变沉积形核理论,当剪切应变积累到一定程度时,临近的短程序原体积的原子区域会优先形成具有一定有序的结构,类似于Sutton等[26]关于Ni-Zr合金晶化过程研究中发现的预晶核,是发生晶化的必要条件。
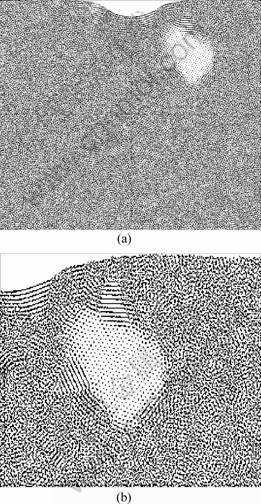
图5 压痕深度1.5 nm时非晶态金属的原子构型图
Fig.5 Amorphous atomic configuration at indentation depth of 1.5 nm: (a) At low magnification; (b) At high magnification
当一个区域的原子受到较大的剪切变形时,随着塑性应变的增加原子会不断从无序态向晶体表面跃迁,从而导致晶核逐渐长大并形成晶粒。晶核的形成、生长与合并是一个非局部协同效应,完全取决于一定范围原子的平均剪切应变情况。当压痕深度达到12 nm时,压头的右下方开始出现纳米晶粒,位置与Hertz弹性接触理论中最大剪应变位置接近,而其它区域的晶化现象不明显。图6所示为有限元计算均匀材料在圆柱压痕作用下的剪应变分布,压头下方的对称位置出现剪应变的极大值。由于金属玻璃的能量与结构的不均匀分布,实际上对称位置不可能同时达到临界晶化,模拟过程中右侧先发生了晶化成核现象。

图6 剪应变分布(有限元计算结果)
Fig.6 Distribution of shear stress (finite element computation result)
2.3 应力晶化方向
图7给出了晶粒生长过程。由图7(a)可见,在金属玻璃的内部有几个原子表现出具有一定结构的晶核。由图7(b)可见,在压头右下方存在比较规则的原子排布,但排列方向相对杂乱。由图7(c)可见,金属玻璃内部出现微小晶粒,表现出明显的主方向,其中包括(111)密排堆积面。图7(d)所示为晶粒的合并生长过程,(111) 方向的晶粒合并了其它方向晶粒。图7(e)所示为晶粒的生长与合并过程,随着晶化区域不断扩大,(111)方向的晶粒不断合并新生成其它方向的晶粒。图7(f) 所示表明,最终的晶化产物具有面心立方结构, 其(111)方向平行于剪切面。

图7 金属玻璃成核、生长与合并过程
Fig.7 Nucleation, growth and coalition processes of metallic glass: (a) d=1.25 nm; (b) d=1.30 nm; (c) d=1.35 nm; (d) d=1.40 nm; (e) d=1.45 nm; (f) d=1.50 nm
由图7(c)可见,初始晶化的方向并不唯一,但小晶粒在剪切作用下不断合并和生长,最终生成的晶粒具有面心立方结构,密排方向(111)与剪切面平行。为探求应力晶化的机制和一般规律,Tarumi等[2, 11]通过实验和分子动力学模拟方法,给出了金属玻璃Ni在纯剪切作用下的晶化方向,本研究得到的规律与他们的结果一致,即密排方向(111)与剪切面平行,说明本研究选取势能函数与模拟过程的正确性。
图8给出了(100), (110), (111) 3个晶体方向平面剪切的能量变化,可以看出,密排方向(111)的晶粒具有最小的能量。最终生成的晶粒具有面心立方结构,其(111)方向平行于剪切面,符合最小能量原则。
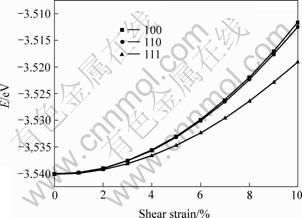
图8 不同方向原子能量—剪切应变关系曲线
Fig.8 Curves of atomic energy vs shear strain in different directions
3 结论
模拟了金属玻璃在压痕过程中的晶化行为,从微观结构演化的角度考察了应力晶化过程中晶粒的形核、长大与合并的演化过程。晶粒生长与合并的区域与Hertz理论符合,发生在具有极大剪切应变的位置。局部较大剪应变导致内部临近的非晶原子形成预晶核,随着塑性应变的增加原子会不断从无序态向晶体表面跃迁,从而导致晶核逐渐长大并形成晶粒。最终生成的晶粒具有面心立方结构,由于最密排面在剪切作用下具有极小的能量,其(111)方向平行于剪切面。
REFERENCES
[1] Schneider S J. Bulk metallic glasses [J]. Phys: Condense Matter, 2001, 13(34): 7723-7736.
[2] Ogura M, Tarumi R, Shimojo M, Takashima K, Higo Y. Control of nanocrystalline orientation using the application of a stress field in an amorphous alloy [J]. Appl Phys Lett, 2001, 79(7): 1042-1044.
[3] Chen H, He Y, Shiflet G J, Poon S J. Deformation-induced nanocrystal formation in shear bands of amorphous alloys [J]. Nature, 1994, 367: 541.
[4] Kim J J, Choi Y, Suresh S, Agron A S. Nanocrystallization during nanoindentation of a bulk amorphous metal alloy at room temperature [J]. Science, 2002, 295(5555): 654-657.
[5] 王美玲,惠希东,董 伟,刘雄军,陈国良. 钨丝增强ZrTiCuNiBeNb金属玻璃基复合材料界面 [J]. 中国有色金属学报,2004,14(10): 1632-1636.
WANG Mei-lin, HUI Xi-dong, DONG Wei, LIU Xiong-jun, CHEN Guo-liang. Interface of W fiber reinforced ZrTiCuNiBeNb bulk metallic glass matrix composite [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(10): 1632-1636.
[6] 陈庆军,范洪波,孙剑飞,沈 军,钱坤明,线恒泽. Fe-Co-Ni-Zr-Mo-W-B块体非晶合金的玻璃形成能力与热稳定性[J]. 中国有色金属学报,2005, 15(10): 1555-1559.
CHEN Qing-jun, FAN Hong-bo, SUN Jian-fei, SHEN Jun, Qian Kun-ming, Xian Heng-ze. Glass-forming ability and thermal stability of Fe-Co-Ni-Mo-W-B bulk amorphous alloys [J]. The Chinese Journal of Nonferrous Metals, 2004, 15(10): 1555-1559.
[7] 卢 柯. 非晶态合金向纳米晶体的相转变 [J]. 金属学报,1994, 30(1): B1-21.
LU Ke. Phase transformation from an amorphous alloy into nanocrystalline materials[J]. Acta Metall Sin, 1994, 30(1): B1-21.
[8] Pang H, Jin Z H, Lu K. Relaxation, nucleation, and glass transition in super cooled liquid Cu [J]. Phy Res B, 2003, 67(9): 94113.
[9] Schuh C A, Lund A C. Atomistic basis for the plastic yield criterion of metallic glass [J]. Nature Materials, 2003, 2(7): 499-452.
[10] Lee B J, Lee C S, Lee J C. Stress induced crystallization of amorphous materials and mechanical properties of nanocrystalline materials: a molecular dynamics simulation study [J]. Acta Materialia, 2003, 51(20): 6233-6240.
[11] Tarumi R, Ogura A, Shimojo M, Takashima K, Higo Y. Molecular dynamics simulation of crystallization in an amorphous metal during shear deformation [J]. Jpn J Appl Phys, 2000, 39(6): B1611-1613.
[12] Mishin Y, Mehl M J, Papaconstantopoulos D A, Voter A F, Kress J D. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations [J]. Phys Rev B, 2001, 63(22): 224106
[13] Daw M S, Baskes M I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals [J]. Phys Rev Lett, 1983, 50(17): 1285-1288.
[14] Daw M S, Baskes M I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals [J]. Phys Rev B, 1984, 29(12): 6443-6453.
[15] 王海龙, 王秀喜, 梁海弋. 金属Cu体熔化与表面熔化行为的分子动力学模拟与分析[J]. 金属学报, 2005, 41(6): 568-572.
WANG Hai-long, WANG Xiu-xi, LIANG Hai-yi. Molecular dynamics simulation and analysis of bulk and surface melting processes for metal Cu [J]. Acta Metallurgica Sinica, 2005, 41(6): 568-572.
[16] 王海龙, 王秀喜, 梁海弋. 金属Cu晶化与玻璃化行为的分子动力学模拟[J]. 化学物理学报,2005, 18(6): 987-992.
WANG Hai-long, WANG Xiu-xi, LIANG Hai-yi. Molecular dynamics simulation of crystallizing and vitrifying Processes for Metal Cu [J]. Chinese Journal of Chemical Physics, 2005, 18(6): 987-992.
[17] Waseda Y. The Structure of Non-crystalline Materials [M]. New York: Mcgraw-Hill, 1980.
[18] Honeycutt J D, Andersen C H. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters [J]. J Phys Chem, 1987, 91(19): 4950-4963.
[19] Brostow W, Dussault J P, Fox B L. Construction of Voronoi polyhedron [J]. J Comput Phys, 1978, 29 (1): 1-92.
[20] Born M, Huang K. Dynamical Theory of Crystal Lattices [M]. Oxford: Clarend Press, 1954.
[21] Nose S. A unified formulation of the constant temperature molecular dynamics methods [J]. J Chem Phys, 1984, 81(1): 511-519.
[22] Parrinello M, Rahman A. Polymophic transitions in single crystals: a new molecular dynamics method [J]. J Appl Phys, 1981, 52(12): 7128-7190.
[23] Lilleodden E T, Zimmerman J A, Folies SM, Nix W D. Atomistic simulation of elastic deformation and dislocation nucleation during nanoindentation [J]. J Mech Phys Solids, 2003, 51(5): 901-920.
[24] 卢 柯,王景唐. 预退火热处理对非晶态Ni-P 合金晶化动力学的影响[J]. 金属学报,1990, 26B: 316-320.
LU Ke, WANG Jing-tang. Effect of pre-annealing on crystallization kinetics of amorphous Ni-P alloys[J]. Acta Metallurgica Sinica, 1990, 26: B316-320.
[25] 卢 柯,王景唐,董 林. 用TEM研究非晶态Ni-P合金薄膜原位加热时的动态晶化过程[J]. 金属学报,1991, 27: B31-B37.
LU Ke, WANG Jing-tang, DONG Lin. In situ observation on dynamic crystallization in amorphous Ni-P alloy foil with TEM[J]. Acta Metallurgica Sinica, 1991, 27: B31-B37.
[26] Sutton M, Yang Y S, Mainville J, Jordan-Sweet J L, Ludwig K F Jr, Stephenson G B. Observation of a precursor during the crystallization of amorphous NiZr2 [J]. Phys Rev Lett, 1989, 62(3): 288-291.
基金项目:国家自然科学基金资助项目(10502047)
收稿日期:2006-05-21;修订日期:2006-11-06
通讯作者:王秀喜,教授;电话:0551-3601283;E-mail: xxwang@ustc.edu.cn
(编辑 龙怀中)