J. Cent. South Univ. Technol. (2010) 17: 187-195
DOI: 10.1007/s11771-010-0029-z 
Robust background subtraction in traffic video sequence
GAO Tao(高韬)1, LIU Zheng-guang(刘正光)1, YUE Shi-hong(岳士弘)1, ZHANG Jun(张军)1,
MEI Jian-qiang(梅建强)1, GAO Wen-chun(高文春)2
1. School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China;
2. Honeywell (China) Limited, Tianjin 300042, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: For intelligent transportation surveillance, a novel background model based on Marr wavelet kernel and a background subtraction technique based on binary discrete wavelet transforms were introduced. The background model kept a sample of intensity values for each pixel in the image and used this sample to estimate the probability density function of the pixel intensity. The density function was estimated using a new Marr wavelet kernel density estimation technique. Since this approach was quite general, the model could approximate any distribution for the pixel intensity without any assumptions about the underlying distribution shape. The background and current frame were transformed in the binary discrete wavelet domain, and background subtraction was performed in each sub-band. After obtaining the foreground, shadow was eliminated by an edge detection method. Experimental results show that the proposed method produces good results with much lower computational complexity and effectively extracts the moving objects with accuracy ratio higher than 90%, indicating that the proposed method is an effective algorithm for intelligent transportation system.
Key words: background modeling; background subtraction; Marr wavelet; binary discrete wavelet transform; shadow elimination
1 Introduction
Identifying moving objects from a video sequence is a fundamental and critical task in many applications of computer-vision. Background subtraction is a method typically used to detect unusual motion in the scene by comparing each new frame with a model of the scene background [1-2]. In traffic video surveillance systems, stationary cameras are typically used to monitor activities on the road. Since the cameras are stationary, the detection of moving objects can be achieved by comparing each new frame with a representation of the scene background. This process is called background subtraction and the scene representation is called background model. Typically, background subtraction is the first stage in automated visual surveillance systems, and the results from background subtraction are used for further processing, such as tracking targets and understanding events. A mixture of Gaussians was used in Ref.[3] to model the intensity of each pixel. The models were learnt and updated for each pixel separately. A mixture of three normal Gaussians distributions was also used in Ref.[4] to model the pixel value for traffic surveillance applications. The pixel intensity was modeled as a weighted mixture of three normal distributions: road, shadow and vehicle distribution. However, in currently existing formulations, temporal adaptation is achieved at a price of slow convergence or large memory requirement, limiting their utility in real-time video applications. In Refs.[5-6], Kalman or Wiener filtering was performed at every pixel. Foreground was detected when the observed intensity was different from the predicted intensity. But visually, it produced the worst foreground masks among all the methods. Even with a large foreground threshold and slow adapting rates, the background model in filtering was easily affected by the foreground pixels. As a result, it typically led to a long trail after a moving object. GUPTE et al [7] modified the background image subtracted from the current image, so that it was looked similar to the background in the current video frame. The background was updated by taking a weighted average of the current background and the current frame of the video sequence. However, since it only used a single previous frame, frame differencing might not be able to identify the interior pixels of a large uniformly-colored moving object. This is commonly known as the aperture problem.
In this work, a new model for background maintenance and subtraction was proposed. A sample of intensity values for each pixel was kept and used to estimate the Marr wavelet probability density function of the pixel intensity. After background modeling, binary discrete wavelet transforms were used for background subtraction. In experiments about the video surveillance on urban road, the model can solve the problem of gradual change of illumination and detect both moving vehicles and foot passengers.
2 Previous background modeling methods
Background modeling is the heart of any background subtraction algorithm. Several models were put forward for background maintenance and subtraction described in introduction. In this work, we only focused on the two most commonly used techniques and excluded the cases that require significant resource for initialization or are too complex.
2.1 Frame-difference background modeling
Frame-difference method [7] obtained the back- ground image as follows:
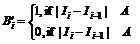 (1)
(1)
where I is the image to be treated. The histogram of the difference image will have high values for low pixel intensities and low values for higher pixel intensities. To set threshold A, a dip is looked for in the histogram that occurs on the right of the peak. Starting from the pixel value corresponding to the peak of the histogram, increasing pixel intensity is searched for a location on the histogram that has a value significantly lower than the peak value (using 10% of the peak value). The corresponding pixel value is used as the new threshold A. Background Bi is:
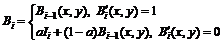 (2)
(2)
Then Bi is the background image. Weight a assigned to the current and instantaneous background affects the update speed, empirically, being determined to be 0.1.
2.2 Mixture of Gaussians background modeling
In mixture of Gaussians (MoG) [8], each pixel location was represented by a number (or mixture) of Gaussians functions that summed together to form a probability distribution function (F):
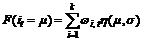 (3)
(3)
If a pixel is a part of the background, the input pixels will be compared to the mean μi of their associated components. If a pixel value is close enough to a given component’s mean, that component will be considered as a matched component. Specifically, to be a matched component, the absolute difference between the pixel and mean must be less than the component’s standard deviation scaled by a factor D: |i-μ|≤Dσ. Then the component variables (ω, μ and σ) are updated to reflect the new pixel value. For the matched components, a set of equations increase the confidence in the component (ω increases, σ decreases, and μ is nudged towards the pixel value). For the non-matched components, the weights decrease exponentially (μ and σ stay the same). The speed change of these variables depends on a learning factor p present in all the equations. Then components that are parts of the background model are determined. First, the components are ordered according to a confidence ω/σ which rewards high ω and low σ. Only M most confident guesses are kept by doing this. Second, a threshold is applied to the component weight ω. The first M components (in order from highest to lowest ω/σ), whose weight (ω) is above the threshold, can be taken as the background model. M is the maximum number of components in the background model, and reflects the number of modes expected in the background probability distribution function (F). Last, foreground pixels are determined. Foreground pixels do not match any components determined to be in the background model.
Robust background modeling method
3.1 Marr wavelet
Marr wavelet [9] is the second derivative of Gaussian smooth function
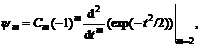
that is:
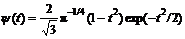 (4)
(4)
The coefficient 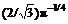 is a guarantee of normalization of ψ(t): ||ψ||2=1. Marr wavelet is widely used in visual information processing, edge detection and other fields. Due to the obvious advantages of extracting characters of the background (especially the edge), Marr wavelet function is used instead of traditional Gaussian function to model the background. The difference of Gaussians (DOG) is a good approximation to Marr wavelet, so DOG is used to approximate Marr wavelet:
is a guarantee of normalization of ψ(t): ||ψ||2=1. Marr wavelet is widely used in visual information processing, edge detection and other fields. Due to the obvious advantages of extracting characters of the background (especially the edge), Marr wavelet function is used instead of traditional Gaussian function to model the background. The difference of Gaussians (DOG) is a good approximation to Marr wavelet, so DOG is used to approximate Marr wavelet:
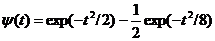 (5)
(5)
3.2 Background modeling
The first frame can be set as the initial background. Considering the dithering of camera, the bias matrix should be obtained before background modeling. The dithering in up-down and left-right planes is mainly concerned. If the background is B and current frame is J, they are firstly processed with two- or three-level Gaussian pyramid decomposition:
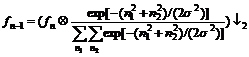 (6)
(6)
where n1=n2=3, and σ=0.5. Suppose the bias matrix is [v, h], and v and h represent the vertical and level dithering parameters, respectively. If the size of fn-1 is M×N, (n-1)-level initial bias matrix will be [vn-1, hn-1], and the maximum pixel value will be fmax, and the minimum one will be fmin. So the bias function is as follows:
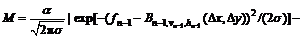
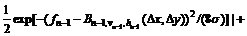
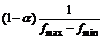 (7)
(7)
where α=0.3; σ=β(fmax-fmin)2; β=0.01; (Δx, Δy) is the offset distance and is changed to obtain the maximum
value D according to  and thus to
and thus to
get the best offset distance (Δxbest, Δybest). [vn-1+Δxbest, hn-1+Δybest] is used as the initial bias matrix for next level fn. By the iterative process, the dithering distance can be finally determined. If the original background after offset correction is B(i, j), and current frame is f(i, j), the probability distribution of deviation between background and current frame is defined as
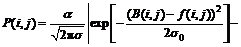
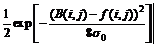 (8)
(8)
The updating weight for background pixel is as follows:
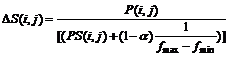 (9)
(9)
The iterative process for updating background is as follows:

 (10)
(10)
where i is the iteration number; N is the frame number; and Bi is the final background.
4 Binary discrete wavelet transform (BDWT) based background subtraction
For one dimension signal f(t), BDWTs [10] are as follows:
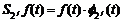 (11)
(11)
 (12)
(12)
where 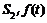 is the projection of f(t) in space Vj; and
is the projection of f(t) in space Vj; and 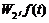 is the projection of f(t) in space Wj. Eqs.(11)- (12) can be rewritten as
is the projection of f(t) in space Wj. Eqs.(11)- (12) can be rewritten as
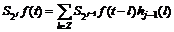 (13)
(13)
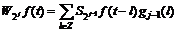 (14)
(14)
For a digital signal d(n)=S1f(t)|t=nT=S1f(n), there exist
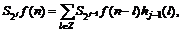 j=1, 2, … (15)
j=1, 2, … (15)
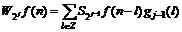 , j=1, 2, … (16)
, j=1, 2, … (16)
where H(z)=(1/4)[-(1/2)z-2+z-1+3+z-(1/2)z2] and G(z)= [(1/4)(z-1-2+z)]. Because the coefficients of the sub-bands of the BDWT are highly correlated, the direction and size are the same as the image, and also, there is no translation in the sub-bands. The difference between digital signals d1(n) and d2(n) is defined as
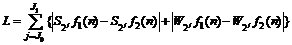
(17)
where J0 and J1 are the starting and ending scales. For a two-dimension digital image, the BDWT is performed to the rows and then the columns. After acquiring L between two frames, the motion area is obtained by setting a threshold which can be obtained automatically by robust segmentation method [11-13]. The noise can be removed by mathematical morphology method. In application, one of the two frames is a background image; the other is the current frame.
5 Shadow removing
In actual test, shadows extracted along with the objects could result in large errors in the object localization and recognition. A method of moving shadow detection based on edge information was proposed, which could effectively detect the cast shadow of a moving vehicle in a traffic scene. In practice, edge detection typically involved the estimation of the first and perhaps the second derivatives of the luminance function, followed by the selection of zero crossings or extrema. For natural images, most shadow scenes were relatively smooth in areas between edges, while large discontinuities occurred at edge locations of the moving object. So shadow could be taken as the sensor noise.
In this work, edge detection depended upon the reliable detection of a non-zero gradient in the luminance function, and the reliable inference of the sign of the second derivative of the luminance function in the gradient direction [14]. The gradient estimates were computed using the two basis functions:
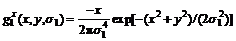 (18)
(18)
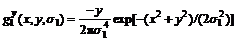 (19)
(19)
The second derivative estimates were computed using the three basis functions:
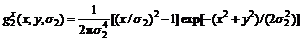
(20)
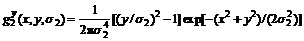
(21)
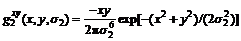 (22)
(22)
where σ1 denotes the scale of the first derivative smoothing kernel; and σ2 denotes the scale of the second derivative smoothing kernel. A multi-scale approach was used for the cases where different scales of sigma were employed: σ1∈[2, 4, 8] and σ2∈[1, 2, 4], so sharp images with little noise required a small scale narrow filter, while blurry noise images required a large scale filter. If the current frame is m, the gradient angle α is:
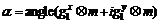 (23)
(23)
Threshold 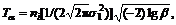 where β=2exp(-6), if |α|<Tα, then α=0. The lap of image m at angle α is:
where β=2exp(-6), if |α|<Tα, then α=0. The lap of image m at angle α is:
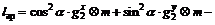
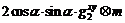 (24)
(24)
Threshold 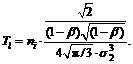 If |lap|<Tl, then
If |lap|<Tl, then
lap=0, and the sensor noise ni=10. For the lap image, edges could be obtained by ‘Canny’ operator. Fig.1 shows the edge detection after removing shadow edge. Eight- direction assimilation method [15-16] was used to fill the edges, combined with the foreground information.

Fig.1 Edge detection without shadow edge: (a) Current frame; (b) Edge detection
6 Experimental results
In this section, the performances of some background modeling techniques were compared: frame- difference, MoG, and Marr-B method that used BDWT- based motion segmentation to perform background subtraction. The video sequences used for testing were taken from urban traffic monitoring cameras. The video was sampled at a resolution of 768×576 and a rate of 15 frame/s. Once the frames were loaded into memory, the Marr-B method averaged 18 frame/s on a 1 400 MHz Celeron CPU. Although grayscale video was used as input, and a grayscale background model was used as output, it was straightforward to extend the algorithm to use color images. The error measurement was used to quantify the degree that each algorithm matched the ground-truth. It was defined in this context as follows:
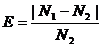 (25)
(25)
where E is the error; N1 is the number of foreground pixels identified by the algorithm; and N2 is the number of foreground pixels in ground-truth.
Fig.2 shows four sample frames of each test video and the background modeling results for every video sequence. The frame numbers of video ‘road’ and ‘car’ are respectively 160 and 224. Fig.3 shows the background subtraction by Marr-B method. Fig.4 shows the background subtraction by frame-difference, and Fig.5 shows background sub-traction by MoG. Fig.6 shows the errors of each method for video sequences ‘road’ and ‘car’, respectively. The experiments show that the frame-difference method has two drawbacks. First, as the foreground objects may have a similar color as the background, these objects cannot be detected by the threshold. Second, the method only slowly adapts to slightly changing environmental conditions. Thus, faster changes as a flashlight signal or fluttering leaves in the wind cannot be modeled. Also, in practice, modeling the background variations with a small number of Gaussian distribution will not be accurate. Furthermore, the very wide background distribution will result in poor detection because most of the gray level spectra will be covered by the background model. Experiments show that Marr-B method is more robust against changes in illumination. Some complicated techniques can also produce superior performance, and the simple method can produce good results with much lower computational complexity. Fig.7 shows the capability of the proposed algorithm to eliminate unwanted shadows. Images in Fig.7(a) are original frames, those in Fig.7(b) are extracted foregrounds, and those in Fig.7(c) are foregrounds after shadow elimination process. Although multiple vehicles with different colors in original image and the vehicle widows are as dark as the shadows, the shadow removal performs well and the vehicles are extracted successfully.

Fig.2 Comparison of background modeling: (a) Video sequence ‘road’; (b) Video sequence ‘car’

Fig.3 Background subtraction by Marr-B method: (a) Video sequence ‘road’; (b) Video sequence ‘car’

Fig.4 Background subtraction by frame-difference: (a) Video sequence ‘road’; (b) Video sequence ‘car’
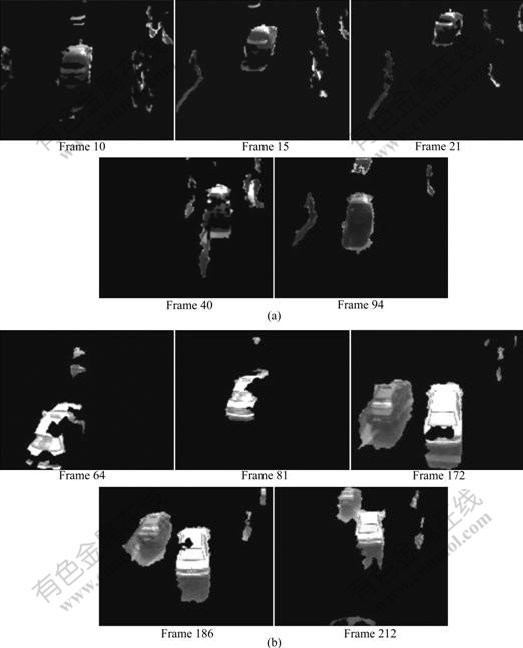
Fig.5 Background subtraction by MoG: (a) Video sequence ‘road’; (b) Video sequence ‘car’
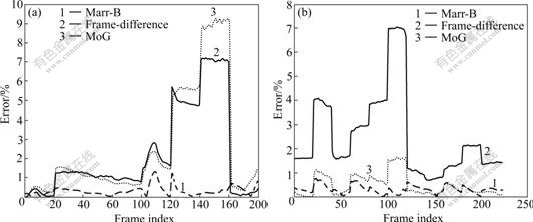
Fig.6 Error measurement of video sequences ‘road’ (a) and ‘car’ (b)

Fig.7 Shadow elimination: (a) Original frames; (b) Extracted foregrounds; (c) Foregrounds after shadow elimination
7 Conclusions
(1) A background modeling and subtraction technique (Marr-B) based on wavelet theory is presented. The background model keeps a sample of intensity values for each pixel in the image and uses this sample to estimate the Marr wavelet probability density function of the pixel intensity.
(2) The density function is estimated using Marr wavelet kernel density estimation technique. Background subtraction is based on BDWT.
(3) Shadow elimination from extracted foreground is based on robust edge information. The method is robust to widely different shadow orientations, shadow appearance and foreground materials such as color and size. No matter how many shadows appear in the video sequence, all these shadows can be precisely eliminated from the background with the proposed method. Future studies lie in improving the robustness against environmental noise and illumination change.
References
[1] GRIMSON W, STAUFFER C, ROMANO R, LEE L. Using adaptive tracking to classify and monitor activities in a site [C]// Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition. Santa Barbara: IEEE Computer Society, 1998: 22-29.
[2] CHEUNG S C, KAMATH C. Robust background subtraction with foreground validation for urban traffic video [J]. Journal on Applied Signal Processing, 2005, 2005(14): 2330-2340.
[3] STAUFFER C, GRIMSON W E L. Adaptive background mixture models for real time tracking [C]// Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition. Fort Collins: IEEE Computer Society, 1999: 246-252.
[4] LEI Bang-jun, XU Li-qun. Real time out door video surveillance with robust foreground extraction and object tracking via multi-state transition management [J]. Pattern Recognition Letters, 2006, 27(15): 1816-1825.
[5] KOLLER D, WEBER J, HUANG T, MALIK J, OGASAWARA G, RAO B, RUSSELL S. Towards robust automatic traffic scene analysis in real-time [C]// Proceedings of the 12th International Conference on Pattern Recognition. Jeiusalem: IEEE Computer Society, 1994: 126-131.
[6] TOYAMA K, KRUMM J, BRUMITT B, MEYERS B. Wallflower: Principles and practice of background maintenance [C]// Proceedings of the IEEE International Conference on Computer Vision. Kerkyra: IEEE Computer Society, 1999: 255-261.
[7] GUPTE S, MASOUD O, MARTIN R F K, PAPANIKOLOPOULOS N P. Detection and classification of vehicles [J]. IEEE Transactions on Intelligent Transportation Systems, 2002, 3(1): 37-47.
[8] LEE D S. Effective Gaussian mixture learning for video background subtraction [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5): 827-832.
[9] van de VILLE D, UNSER M. The Marr wavelet pyramid [C]// Proceedings of the 15th IEEE International Conference on Image Processing. San Diego: IEEE Computer Society, 2008: 2804-2807.
[10] SWANSON M D, TEWFIK A H. A binary wavelet decomposition of binary images [J]. IEEE Transactions on Image Processing, 1996, 5(12): 1637-1650.
[11] CHEN Song-can, ZHANG Dao-qing. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure [J]. IEEE Transactions on Systems, Man, and Cybernetics, 2004, 34(4): 1907-1916.
[12] ZHOU Xian-cheng, SHEN Qun-tai, LIU Li-mei. New two-dimensional fuzzy C-means clustering algorithm for image segmentation [J]. Journal of Central South University of Technology, 2008, 15(6): 882-887.
[13] LI Xiao-he, ZHANG Tai-yi, QU Zhan. Image segmentation using fuzzy clustering with spatial constraints based on Markov random field via Bayesian theory [J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2008, 91(3): 723-729.
[14] ELDER J H, ZUCKER S W. Local scale control for edge detection and blur estimation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(7): 699-716.
[15] GAO Tao, LIU Zheng-guang, ZHANG Jun. BDWT based moving object recognition and Mexico wavelet kernel mean shift tracking [J]. Journal of System Simulation, 2008, 20(19): 5236-5239.
[16] XIAO Mei, HAN Chong-zhao, ZHANG Lei. Moving shadow detection and removal for traffic sequences [J]. International Journal of Automation and Computing, 2007, 4(1): 38-46.
Foundation item: Project(60772080) supported by the National Natural Science Foundation of China; Project(3240120) supported by Tianjin Subway Safety System, Honeywell Limited, China
Received date: 2009-03-10; Accepted date: 2009-09-12
Corresponding author: GAO Tao, Doctoral candidate; Tel: +86-22-28213076; E-mail: taogao@its.la
(Edited by CHEN Wei-ping)