High temperature deformation behavior and mechanism of
spray deposited Al-Fe-V-Si alloy
XIAO Yu-de(肖于德), WANG Wei(王 伟), LI Wen-xian(黎文献)
School of Materials Science and Engineering, Central South University, Changsha 410083, China
Received 15 July 2007; accepted 10 September 2007
Abstract: Al-8.5Fe-1.3V-1.7Si alloy was prepared by spray deposition and hot extrusion. The high temperature plastic deformation behavior of the spray deposited Al-8.5Fe-1.3V-1.7Si alloy was investigated in the strain rate range of 2.77×10-4-2.77×10-2 s-1 and temperature range of 350-550 ℃ by Gleebe-1500 thermomechanical simulator. The mechanism of the high temperature plastic deformation of the alloys was studied by TEM associated with the analysis of Rosler-Artz physical constitutive relationship based on the model of dislocation detaching from dispersion particles. The results show that Al-Fe-V-Si alloy has low strain hardening coefficient, and even exhibits work softening. Stress exponent n and activation energy Q were calculated based on Zener-Hollomon relation and Rosler-Artz physical model respectively. The Rosler-Artz physical model can give a good prediction for the abnormal behavior of high temperature deformation of spray deposited Al-Fe-V-Si alloy, that is, n larger than 8 and Q higher than 142 kJ/mol. However, because of the highly refined microstructure, the high temperature deformation behavior of spray deposited Al-Fe-V-Si alloy deviates more or less from the law predicted by using Rosler-Artz physical model.
Key words: spray deposition; heat-resistant aluminum alloy; constitutive equation; high temperature plastic deformation; stress exponent; activation energy; dislocation detachment
1 Introduction
Rapidly solidified Al-Fe-V-Si heat resistance aluminum alloy is a kind of light-mass structural materials with high specific strength, high specific stiffness and good heat-resistance[1-5]. It is able to be applied in the temperature range of 150-350 ℃ (and even higher temperature) to replace some of titanium alloys or steels, meeting the needs of advanced space shuttle, aircrafts and missiles to achieve high flying velocity and large carrying capacity in the modern space-flight and aviation industries[6-8]. Spray deposition technique can be used to develop large-scale structural materials of the rapidly solidified Al-Fe-V-Si alloy, substituting for the rapid solidification-powder metallurgical process.
Spray deposited Al-Fe-V-Si alloy should be hot worked at high temperature (400-500 ℃) and used in the temperature range from 150 ℃ to 350 ℃[9-12]. Consequently, it is important to understand the high temperature deformation behavior and mechanism of the spray deposited Al-Fe-V-Si alloy. A number of models regarding to the high temperature deformation behavior and mechanism, such as Ansell-Weertman model, critical stress model and Rosler-Artz physical model, have been discussed recently[13-20]. Ansell-Weertman reported that dislocation can climb the dispersed particles or loop the particles according to Orowan mechanism, as a result, the size of the dispersed particles influenced the creep process directly. In critical stress model, MISHA et al[20-21] reported that the creep behavior of dispersed alloys can be describe by
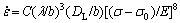(1)
where C is a material constant, σ0 the critical stress, λ the mean particle space, b the length of Burgers vector, DL the coefficient of volume self-diffusion, DL=DL0? exp(-QL/RT), QL the activation energy of crystal diffusion of aluminum alloy, QL≈142 kJ/mol. CARRENO and RUANO[22] utilized this model to describe the creep behavior of rapidly solidified Al-Fe-V-Si alloy. However, the model was unable to give a proper interpretation about the facts that its stress exponent value is much larger than 8, and activation energy larger than 142 kJ/mol.
Recently, ROSLER et al[1-2] reported a new concept in explaining the creep behavior of dispersion reinforced alloys. The creep rate controlled by thermally activated detachment of dislocations from dispersed particles can be expressed as
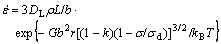(2)
where ρ is the movable dislocation density, σ the applied stress, G the shear modulus, k the relaxation parameter, which describes the decrease in the dislocation line energy at the particle/matrix interface, r the average particle radius, σd the athermal detachment
stress,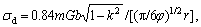 
φ volume fraction of dispersed particles, kB the Boltzmann constant, and T the absolute temperature. The Rosler-Artz physical model can be applied to describe the high temperature deformation behavior of conventional alloys well [23-24].
Spray deposited Al-Fe-V-Si alloy is characterized by the typical microstructures with plenty of nano-sized Al12(Fe,V)3Si particles distributed uniformly in the submicron size α(Al) matrix. As a result, its high temperature deformation behavior might be different from that of the conventional aluminum alloys. In this study, high temperature deformation behavior of the spray deposited Al-Fe-V-Si alloy is investigated, and its deforming mechanism is discussed by using the Rosler-Artz physical model.
2 Experimental
The materials used in this work were spray deposited Al-8.5Fe-1.3V-1.7Si alloy. They were extruded after spray deposition and the extrusion ratio is 6.3.
The thermo-mechanical simulation was carried out in the strain rate range of 2.77×10-4-2.77×10-2 s-1 and temperature range of 350-550℃ in Gleebe-1500 thermomechanical simulator. The heating rate is 2 ℃/s and the max deformation ratio is 40%. The deformation process was controlled by computer and the computer collected the data automatically.
The transmission electron microscope samples were prepared by double-jet electro-polishing in the mixed solution of 25% nitric acid and 75% methanol. The microstructure observation and analysis of the samples were performed on TecnaiG220 transmission electron microscope with an accelerating voltage of 200 kV.
3 Results and discussion
3.1 True stress—true strain curve of high temperature deformation of spray deposited Al-Fe-V-Si alloy
The true stress vs true strain curves of the high temperature deformation of Al-8.65Fe-1.32V-1.75Si alloy on different conditions are shown in Fig.1. The peak flow stresses of Al-8.65Fe-1.32V-1.75Si alloy on different deformation conditions are listed in Table 1. The flow stress increases with the increasing of the strain at the beginning of deformation, exhibiting work hardening effect. After the flow stress achieves its peak rapidly, the flow stress decreases gradually, behaving
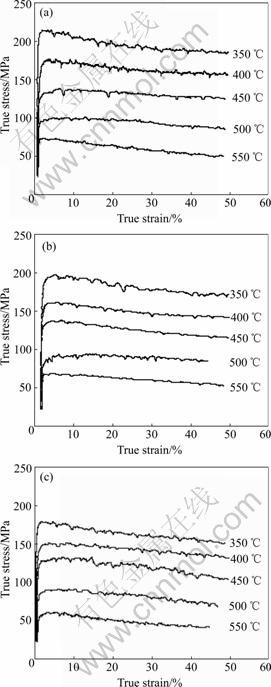
Fig.1 True stress—true strain curve of high temperature deformation of spray deposited Al-Fe-V-Si alloy: (a) 2.77×10-2 s-1; (b) 2.77×10-3 s-1; (c) 2.77×10-4 s-1
Table 1 Peak flow stresses of Al-8.65Fe-1.32V-1.75Si alloy on different high temperature deformation conditions
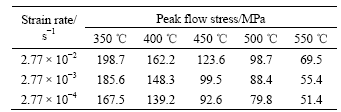
like work softening. The recrystallization temperature of rapidly solidified Al-8.5Fe-1.3V-1.7Si alloy is up to 550℃[24-25], hence it might be intense dynamic recovery that results in the work softening effect. This indicates that Al-Fe-V-Si alloy has low strain hardening coefficient, and even exhibits work softening during plastic deformation at the high temperature of 350-550 ℃.
When the strain rate is fixed, the flow stress declines and the irregular fluctuation of the stress is weakened with the increase of the temperature. Under the same deformation temperature, the flow stress increases with the elevation of the strain rate. This indicates that Al-Fe-V-Si alloy is a kind of materials sensitive to positive strain.
3.2 Discussion of high temperature deformation of Al-Fe-V-Si alloy based on Zener-Hollomon relation
The relationship between the steady flow stress σ and strain rate 
of high temperature deformation of the materials can be described as the follows[26-27].
At low stress level (ασ＜0.8):
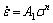(3)
At high stress level (ασ＞1.2):
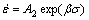(4)
where n ,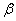
, A1 and A2 are constants.
Considering that high temperature deformation of Al-Fe-V-Si alloy is regarded as a thermal activation process, this process can be characterized by[27-28]
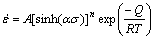(5)
where A, σ are constants, n the stress exponent, R the gas constant, R=8.314 J/(mol·K), T absolute temperature, and Q deformation activation energy.
From Eqns.(4) and (5), the relationship among α, β and n can be expressed as
α=β/n (6)
Meanwhile, Eqns.(4) and (5) can be modified as
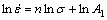(7)
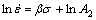(8)
As shown in Figs.2(a) and (b), n and β can be obtained by linear regression from Eqns.(3) and (4), respectively, and α=0.010 4 MPa-1 can be calculated by Eqn.(6). Hence, from Eqn.(3), The stress exponent n and activation energy Q can be obtained:
(9)
(10)
where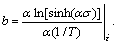 
The calculated n and Q
values from Figs.2(c) and (d) are listed in Table 2. The stress exponents n of spray deposited Al-Fe-V-Si alloy during high temperature deforming process are larger than 8, and increase firstly and then descent with elevation of deforming temperature. The values of activation energy Q are much higher than that of conventional aluminum alloys (142 kJ/mol), and also ascend firstly and then decline with the increasing of deforming temperature. Additionally, the activation energy Q increases with the decreasing of the strain rate.
3.3 High temperature deformation mechanism of spray deposited Al-Fe-V-Si alloy based on Rosler-Artz physical model
During the high temperature deformation process of
Table 2 Stress exponent n and activation energy Q calculated by Zener-Hollomon relation
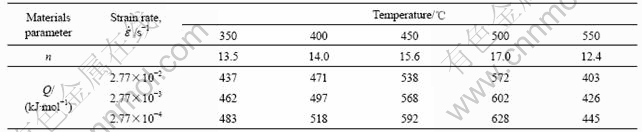
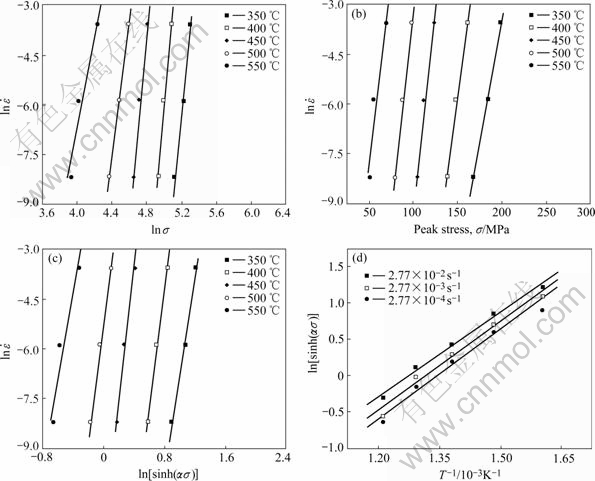
Fig.2 Relationships among peak flow stress σ, flow strain 
and deforming temperature T of high temperature deformation of spray deposited Al-Fe-V-Si alloy: (a) 
vs ln σ; (b) vs σ; (c) vs lnsinh(ασ); (d) lnsinh(ασ) vs 1/T
spray deposited Al-Fe-V-Si alloy, the attraction between particles and dislocations as well as the dislocation detachment process can be observed, as shown in Fig.3. This implies that high temperature deformation process of Al-Fe-V-Si alloy can be described by the Rosler-Artz physical model[1-2].
Eqn.(1) can be modified as
(11)
where
Fig.3 TEM micrograph of dislocation detaching from particles
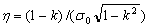(12)
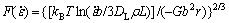(13)
Suppose that the aluminum matrix in the spray deposited Al-Fe-V-Si alloy can be treated as pure aluminum[28], then G/MPa=3.0×104-16T, DL=1.71×10-4exp(-142 120/RT), φ=27%, r=30 nm and ρ=1.3×1013 m-2. As shown in Fig.4, η can be calculated by linear regression from Eqn.(11) and k as well as σd can be obtained. The calculated values of k and σd are listed in Table 3.
By partial differentiation of Eqn.(1), the apparent stress exponent (napp) and the apparent activation energy (Qapp) can be expressed as Eqn.(14) and Eqn.(15), respectively:
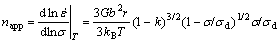(14)
Table 3 Calculated values of relaxation parameter k, athermal detachment stress σd, stress exponent napp and activation energy Qapp based on Rosler-Artz physical model
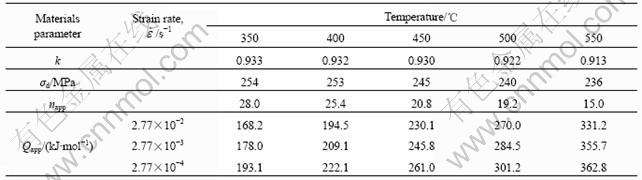
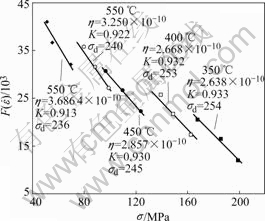
Fig.4 Linear relationship between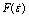 
and σ
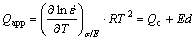(15)
The values of napp and Qapp under different deformation conditions are listed in Table 3. This suggests that napp descends with the enhancement of the deformation temperature and the values of napp are larger than 8. Meanwhile, the values of Qapp increase with the ascending of deformation temperature and the declining of the strain rate. The values of Qapp are larger than 142 kJ/mol. The Rosler-Artz physical model can interpret the facts that the values of napp are larger than 8 and those of Qapp are larger than 142 kJ/mol during the high temperature deformation process. However, the variation trends of napp and Qapp suggested by the Rosler-Artz physical model are not conformed to the results calculated by Zener-Hollomon relation. The aberrancy could be due to high refinement of α(Al) grains and Al12(Fe, V)3Si particles, and additionally might be result from microstructural evolution during high temperature deformation process, which will be investigated much in the further studies.
4 Conclusions
1) The Al-Fe-V-Si alloy is a kind of materials sensitive to positive strain and having low strain hardening coefficient, and even exhibiting work softening during plastic deformation at the high temperature of 350-550 ℃.
2) The stress exponent n and the activation energy Q of spray deposited Al-Fe-V-Si alloy during the high temperature deformation process are much higher than those of conventional aluminum alloys (8 and 142 kJ/mol), and both n and Q increase firstly and then decrease with elevation of deforming temperature.
3) The Rosler-Artz physical model can interpret the facts that the values of napp are larger than 8 and those of Qapp are larger than 142 kJ/mol during the high temperature deformation process. However, the variation trends of napp and Qapp suggested by the Rosler-Artz physical model are not conformed to the results calculated by Zener-Hollomon relation.
References
[1] ROSLER J, ARZT R. A new model-based creep equation for dispersion strengthened materials [J]. Acta Metallurgica, 1990, 38: 671-683.
[2] ROSLER J, JOOS R, ARZT R. Microstructure and creep properties of dispersion-strengthened aluminum alloys [J]. Metallurgical Transaction A, 1992, 23A: 1521-1539.
[3] KIM I S, KIM N J, NAM S W. Temperature dependence of the optimum particle size for the dislocation detachment controlled creep of Al-Fe-V-Si/SiCp composite [J]. Scripta Metall, 1995, 32: 1813-1819.
[4] ART E, WILKINSON P S. Threshold stresses for dislocation climb over hard particles: The effect of an attractive interaction [J]. Acta Metallurgica, 1986, 34: 1893-1898.
[5] SATOH T, OKIMOTO K, NISHIDA S. High temperature deformation behavior of aluminum alloys produced from centrifugally-atimized powders [J]. Journal of Materials Processing Technology, 1997, 68: 221-228.
[6] SPIGARELLI S. Interpretation of creep behaviour of dispersion-strengthened Al-Fe-V-Si alloys in terms of detachment mechanisms: An overview [J]. Mater Sci Eng, 2002, A337: 306-314.
[7] LIN J, DEAN T A. Modelling of microstructure evolution in hot forming using unified constitutive equations [J]. Journal of Materials Processing Technology, 2005, 167: 354-362.
[8] MYHR O R, GRONG O, FJAER H G, MARIOARA C D. Modelling of the microstructure and strength evolution in Al-Mg-Si alloys during multistage thermal processing [J]. Acta Mater, 2004, 52: 4997-5008.
[9] MCQUEEN J, RYAN N D. Constitutive analysis in hot working [J]. Mater Sci Eng A, 2002, 322: 43-63.
[10] ENGDAHL T, HANSEN V, WARREN P J, STILLER K. Investigation of fine scale precipitates in Al-Zn-Mg alloys after various heat treatments [J]. Mater Sci Eng A, 2002, 327: 59-64.
[11] ROBSON J D. A new model for prediction of dispersoid precipitation in aluminium alloys containing zirconium and scandium [J]. Acta Mater, 2004, 52: 1409-1421.
[12] PETER A L, RICHARD P D. An artificial neural network approach to multiphase continual constitutive modeling [J]. Composites Part B: Engineering, 2007, 38: 817-823.
[13] STARINK M J, WANG S C. A model for the yield strength of overaged Al-Zn-Mg-Cu alloys [J]. Acta Mater, 2003, 51: 5131-5150.
[14] EBRAHIMI R, ZAHIRI S H, NAJAFIZADEH A. Mathematical modelling of the stress—strain curves of Ti-IF steel at high temperature [J]. Journal of Materials Processing Technology, 2006, 171: 301-305.
[15] CLAYTON J D, MCDOWELL D L, BAMMANN D J. Modeling dislocations and disclinations with finite micropolar elastoplasticity [J]. International Journal of Plasticity, 2006, 22: 210-256.
[16] LANG Li-hui, LI Tao, ZHOU Xian-bin, KRITENSEN B E, DANCKERT J, NIELSEN K B. Optimized constitutive equation of material property based on inverse modeling for aluminum alloy hydroforming simulation [J]. Trans Nonferrous Met Soc China, 2006, 16(6): 1379-1385.
[17] MA A, ROTERS F, RAABE D. A dislocation density based constitutive model for crystal plasticity FEM including geometrically necessary dislocations [J]. Acta Materialia, 2006, 54: 2169-2179.
[18] MA A, ROTERS F, RAABE D. On the consideration of interactions between dislocations and grain boundaries in crystal plasticity finite element modeling—Theory, experiments, and simulations [J]. Acta Materialia, 2006, 54: 2181-2194.
[19] CHINH N Q, ILLY J, HORITA Z, LANGDON T G. Using the stress–strain relationships to propose regions of low and high temperature plastic deformation in aluminum [J]. Mater Sci Eng A, 2005, 410/411: 234-238.
[20] MISHRA R S, PARADKAR A G, RAO K N. Steady state creep behavior of a rapidly solidified and further progress [J]. Acta Metal Mater, 1993, 41: 2243-2251.
[21] MISHRA R S, PANDEY A B. Some observations on the high-temperature creep behavior of 6061 Al-SiC composites [J]. Metall Trans A, 1990, 21: 2089-2090.
[22] CARRENO F, RUANO O A. Separated contribution of particles and matrix on the creep behavior of dispersion strengthened materials [J]. Acta Mater, 1998, 46: 159-167.
[23] DOBES F. Interpretation of the creep behaviour of dispersion-strengthened Al-Fe-Ni alloys in terms of the detachment mechanism [J]. Mater Sci Eng A, 1995, 194: 19-21.
[24] CARRENO F, PEREZ-PARDO M T, GONZALEZ-DONCEL G. Texture stability of a rapidly solidified dispersion strengthened Al-Fe-V-Si [J]. Scripta Materialia, 1998, 38: 1427-1433.
[25] KIM D H, CANTOR B. Structure and decomposition behavior of rapidly solidified Al-Fe alloys [J]. Journal of Materials Science, 29: 2884-2892.
[26] ZHOU M, CLODE M P. A constitutive model and its identification for the deformation charactered by dynamic recovery [J]. Transactions of the ASME, 1997, 119: 138-142.
[27] ESTRIN Y. Dislocation theory based constitutive modeling: Foundations and applications [J]. Journal of Materials Processing Technology, 1998, 80: 8-15.
[28] PENG L M, ZHU S J, MA Z Y, CHEN H R, WANG F G. High temperature creep deformation of an Al-Fe-V-Si alloy [J]. Mater Sci Eng A, 1999, 259: 25-33.
(Edited by YANG Bing)
Corresponding author: XIAO Yu-de; Tel: +86-731-8837456; E-mail: xiaoyude@mail.csu.edu.cn
