DOI: 10.11817/j.issn.1672-7207.2015.10.021
海上风电传输中MMC的模型预测控制
周云1,夏向阳1,孔祥霁1,范家铭1,赵相涛2
(1. 长沙理工大学 电气与信息工程学院,湖南 长沙,410077;
2. 国网山东省电力公司济宁供电公司,山东 济宁,272000)
摘要:针对海上风电柔性直流输电系统(HVDC)中模块化多电平换流器(MMC)的循环电流抑制及MMC中子模块电容电压平衡问题,提出一种模型预测控制(MPC)策略。该方法根据系统的离散时间数学模型,开发对应的预测控制方式,将每个MMC单元中最佳的开关状态问题转化为求目标函数的最优化问题,以抑制环流,并实现MMC单元的电容电压平衡。最后利用MATLAB/SIMULINK进行仿真验证,研究结果表明:该模型预测控制策略是有效的和可行的,且实现原理简单,适用于海上风电传输的MMC-HVDC系统。
关键词:模块化多电平换流器;模型预测控制;电容电压平衡;循环电流控制;海上风电
中图分类号:TM76 文献标志码:A 文章编号:1672-7207(2015)10-3703-07
Model predictive control of modular multilevel converter for offshore wind power transmission
ZHOU Yun1, XIA Xiangyang1, KONG Xiangji1, FAN Jiaming1, ZHAO Xiangtao2
(1. College of Electrical and Information Engineering,
Changsha University of Science and Technology, Changsha 410077, China;
2. Jining Power Supply Company, State Grid Shandong Electric Power Company, Jining 272000, China)
Abstract: For the circulating currents suppression of modular multilevel converter (MMC) and the equalizing voltages of sub-module capacitor of flexible high voltage direct current(HVDC) system for offshore wind, a model predictive control (MPC) strategy was proposed, the corresponding prediction model was developed according to discrete-time mathematical model of the system, and the best switching state in each MMC unit was obtained by solving an objective function optimization problem to eliminate the circulating currents and achieve the voltage balancing task of DC capacitor. Finally, MATLAB/SIMULINK was used to simulate the control strategy. The results show that the model predictive control strategy is effective and feasible, its implementation principle is easy and simple, and it is suitable for MMC-HVDC system of offshore wind power transmission.
Key words: modular multilevel converter (MMC); model predictive control (MPC); capacitor voltage balancing; circulating current control; offshore wind power
在可再生能源开发中,风力发电技术是最成熟、最具商业化发展前景的发电形式之一[1],近年来,由于土地资源短缺,海上风电凭借其风速高、噪音小、风力稳定及发电量大等诸多优势,在世界范围内得到迅速发展[2-3]。截至2011年底,全球海上风电总装机容量达到4.954 GW,其中,我国2011年海上风电累计为241.3 MW。另外,我国提出了到2020年海上风电总装机容量为30 GW的目标,发展海上风电已成为未来风电发展的主要方向。随着海上风电机组容量和风电场的规模不断增大,基于模块化多电平换流器的柔性直流输电(modular multilevel converter-high voltage direct current, MMC-HVDC)系统得到越来越多的关注和研究[4-6],与VSC-HVDC相比,MMC-HVDC系统有效地减少了输出电压的谐波含量,降低了功率器件开关频率和损耗,实现高电压大功率的运行[7-8],非常适合于长距离、大容量的海上风电传输。然而,MMC拓扑自身也存在一些不足:由于分布式布置的储能电容,其功率单元电容电压脉动较大以及各相之间能量分配不平衡,这不仅会使本来正弦的桥臂电流发生畸变,而且还提高了器件的额定电流容量,进一步增加了系统成本等[9]。MMC子模块间电容电压的均衡分配与桥臂间存在的循环电流问题成为MMC亟需解决的难点,有必要采用合适的控制策略对电容电压平衡和环流进行协同控制。丁冠军等[10]介绍了MMC子模块的拓扑机制与调制策略,采用基频开关调制时子模块导通角度的计算方法,但没有给出与其配合的电容均压策略。Hagiwara等[11]提出对调制波进行微调的形式来实现电容电压的平衡,但此方法需要与脉冲宽度调制相配合,这使得换流器每个子模块所用的调制波不一样,子模块越多就越难以实现。屠卿瑞等[9]推导了MMC在运行中相间环流的解析表达式,并针对环流抑制给出了MMC桥臂电抗器的计算方法。梁帅奇等[12-14]给出了一种基于上桥臂和下桥臂的平均直流电容的电压差值进行环流抑制的方法,并通过实验验证,但该方法需用到所有功率单元的直流电容电压,对系统信号采集环节提出了较高要求。为此,本文针对应用于海上风电柔性直流输电领域的MMC子模块电容电压平衡及换流器内部存在的循环电流抑制问题,提出一种模型预测控制(MPC)策略,根据柔性直流输电系统的离散时间数学模型,开发对应于离散时间模型的预测模型。利用它的目标函数最优化技术,并使用预测模型来选择每个MMC单元中最佳的开关状态,来抑制循环电流,并通过冗余开关状态达到电容电压平衡。最后,通过MATLAB/SIMULINK仿真验证该策略的有效性和可行性。
1 MMC-HVDC的基本结构
图1所示为MMC-HVDC系统的结构图。该系统由2个换流站及直流线路组成,送端、受端换流器均采用MMC拓扑,则2个换流器具有相同的结构,分别为图1中MMC1和MMC2。MMC的交流侧通过串联电阻器R和电感器L以及三相变压器T连接到公用电网,交流系统由等值电源Us和等值电感LAC表示,直流侧电压用Vdc表示。每个MMC单元的同步控制信号从对应的变压器低压侧提取。
图2所示为MMC主电路结构图。由图2可知:每个MMC单元各相均有2个桥臂(即上桥臂和下桥臂),其中每个桥臂由n个相互连接且结构相同的半桥式子模块SM(sub-module)与一系列电抗器串联构成,相臂内的电抗器l是用来抑制桥臂间因总直流电压差异引起的相间环流。系统结构具有高度模块化特点,子模块之间可以互换,具有很强的扩展性和灵活性。
2 MMC的模型预测控制策略
2.1 MMC基本运行原理
构成模块化多电平的基本功率单元SM由1个直流储能电容C和2个绝缘栅双极晶体管(insulated gate bipolar transistor,IGBT)半桥组成,其拓扑如图3所示。图3中:VSM为子模块的输出电压;iSM为子模块的充放电电流;Vc为子模块的瞬时电容电压。
从图3可知:每个功率单元都是两端元件,通过2个开关器件T1和T2的作用;VSM可以实现在电容电压Vc与0之间的切换,从而调整桥臂输出电平的个数。子模块4种常用的工作状态如表1所示。

图1 MMC-HVDC系统结构
Fig. 1 Typical structure of MMC-HVDC system

图2 MMC主电路结构图
Fig. 2 Main circuit structure of MMC

图3 单个子模块结构
Fig. 3 Structure diagram of single sub-module
表1 MMC子模块的常用工作状态
Table 1 Common working states of SM in MMC

理论上,各子模块构成的桥臂电压均可等效成1个可控电压源vPjk和vNjk(j为a,b和c,表示三相;k为1和2,分别对应MMC1和MMC2系统)[15];下标P表示上桥臂;下标N表示下桥臂;iPjk和iNjk为相应桥臂电流。
为了维持直流电压稳定,一般要求MMC同相上、下2个桥臂的子模块互补对称投入,即满足
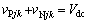 (1)
(1)
在任意时刻,每一相有且仅有n个子模块导通n个子模块关断,则开关管的导通个数必须满足
 (2)
(2)
假设每个SM电容电压理想调节为Vdc/n,在MMC中的各相端子,1个理想的(n+1)的电平波形,相对于1个虚构的直流侧中点t,交流侧的输出电压满足如下关系[9]:
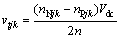 (3)
(3)
式中:vtjk为MMCk中交流侧的相电压。由式(3)可知:vtjk在Vdc/2和-Vdc/2范围内,以步长为Vdc/n呈阶梯状变化。在实际运行过程中,MMC中各个SM电容电压应被实时监测且维持平衡,即通过使用有源电压平衡技术使各个子模块电容电压维持其额定值Vdc/n。
根据MMC的三相对称性,以MMC1为例,环流等值电路图如图4所示。其中:ijk为相电流。相应的臂电流描述如下:
 (4)
(4)
 (5)
(5)
其中:iCir jk为流过MMCk中j相的循环电流。环流分量叠加在桥臂电流中,增加了器件的额定容量,增大了换流器的损耗,导致子模块电容电压的波动,严重时还会造成系统不稳定。因此,为了最大限度地减少其负面影响,应该设计相应的控制策略对环流进行有效抑制。

图4 MMC1环流等值电路图
Fig. 4 Circulation equivalent circuit diagram in MMC1
2.2 MMC的数学模型
据基尔霍夫电压定理,MMCk中j相动态数学方程如下:
 (6)
(6)
式中:vsjk为变压器低压侧的电网电压。根据式(4)~(6),推导交流侧相电流ijk与环流iCir jk分别为
 (7)
(7)
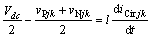 (8)
(8)
由式(7)和(8)可知:交流侧相电流受上、下桥臂电压之差的影响,而上、下桥臂电压之和与直流电压不相等是内部环流产生的根本原因。
图2中MMC单元的SM电容电压的动态开关描述为
 (9)
(9)
其中:i=1,2,…,n;j=a,b,c;k=1,2。若在上桥臂中的子模块,则iCijk=iPjk;若在下桥臂中的子模块,iCijk=iNjk。
2.3 模型预测控制策略
模型预测控制(MPC)是一类特殊的控制,具有控制效果好、鲁棒性强等优点,其本质是在每一个采样瞬间通过求解1个有限时域开环最优控制问题。在前面MMC的数学模型基础上,本文提出一种改进的MPC控制策略,控制交流侧电流,同时调节SM的电容电压平衡,并抑制循环电流。其实现过程如下:首先,为MMC变量正向预测其离散时间模型;然后,定义与控制目标相关的目标函数;最后,选择换流器所有可能的最好状态来评估定义的目标函数,得到所定义的目标函数的最小值[16]。
2.3.1 交流侧电流控制
电流控制的目的是调节MMC交流侧电流与参考值一致(即参考电流跟踪)。在式(7)的基础上,假设1个采样周期Ts,用欧拉近似推导出的电流导数作为MMC交流侧电流的预测模型如下:

 (10)
(10)
式中:L′=L+l/2,K′=R+L′/Ts;ijk(t+Ts)为交流侧电流的预测值;ijk(t)为实际测定值;vsjk(t+Ts)为变压器低压侧电网电压的预测值,假设Ts足够小时,可近似为测定值vsjk(t);vPjk(t+Ts)和vNjk(t+Ts)分别为上、下桥臂电压的预测值,它的计算可通过增加一步向前预测上桥臂和下桥臂投入子模块的电容电压来获得。
为了减小预测电流和参考电流之间的误差,定义与电流误差有关的目标函数为
 (11)
(11)
式中:ijk ref为参考电流,它根据预先设定传递到交流系统的有功和无功功率求得。在理想情况下,若交流侧电流跟踪参考值,目标函数Jjk达到其最小值0,则这种情况被作为交流侧电流控制的理想状态。在每个采样期间,Jjk为MMC所有可能的开关状态计算并比较,从而得到式(11)的最小值,作为下一个开关周期最佳的开关状态。
2.3.2 电容电压平衡
根据式(9),电容电压的下一个预测值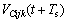 的计算方法为:
的计算方法为:
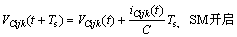 (12)
(12)
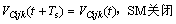 (13)
(13)
对于上桥臂的子模块,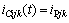 ;对于下桥臂的子模块,
;对于下桥臂的子模块, 。为了实现电容电压均衡,改进的MPC策略需在原始的目标函数基础上,通过引入1个附加项,得出子模块电容电压与它们参考值之间的电压偏差。因此,目标函数修改为
。为了实现电容电压均衡,改进的MPC策略需在原始的目标函数基础上,通过引入1个附加项,得出子模块电容电压与它们参考值之间的电压偏差。因此,目标函数修改为
 (14)
(14)
式中: 为加权因子,其调整是基于分配给电容电压偏差的成本贡献。该过程基于经验方法完成,具体过程见文献[17]。
为加权因子,其调整是基于分配给电容电压偏差的成本贡献。该过程基于经验方法完成,具体过程见文献[17]。
2.3.3 循环电流控制
基于式(8),推导出循环电流的离散时间预测模型如下:
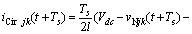
 (15)
(15)
改进的MPC策略目的是通过添加式(15)中第3项来抑制循环循环电流,与循环电流相关的目标函数如下:

 (16)
(16)
式中: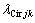 为加权因子,其调整是基于分配给循环电流的成本贡献[17]。每个MMC单元的MPC策略框图见图5。
为加权因子,其调整是基于分配给循环电流的成本贡献[17]。每个MMC单元的MPC策略框图见图5。

图5 MMC单元的MPC策略框图
Fig. 5 Block diagram of MPC strategy for MMC
在1个(n+1)电平MMC中,共有 个可能的开关状态。MPC策略根据MMCk中j相所有可能的开关状态来评估目标函数
个可能的开关状态。MPC策略根据MMCk中j相所有可能的开关状态来评估目标函数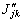 ,选择开关状态使
,选择开关状态使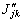 到达最小值,此状态就作为所需的开关状态。图5所示为海上风电传输系统中每个MMC单元的MPC策略的具体实现过程。在每个采样周期Ts内,跟踪参考电流,把每个MMC单元中最佳的开关问题转化为求目标函数的最优化问题,并采用冗余开关状态形式,实现SM电容电压平衡和抑制循环电流。
到达最小值,此状态就作为所需的开关状态。图5所示为海上风电传输系统中每个MMC单元的MPC策略的具体实现过程。在每个采样周期Ts内,跟踪参考电流,把每个MMC单元中最佳的开关问题转化为求目标函数的最优化问题,并采用冗余开关状态形式,实现SM电容电压平衡和抑制循环电流。
3 仿真分析
3.1 仿真模型及参数
为了验证海上风电柔性直流输电系统中模型预测控制策略的有效性和可行性,利用MATLAB/SIMULINK软件对三相MMC模型进行仿真验证。采用MMC单元精确开关模型,主电路结构如图1所示。选定每相桥臂级联的功率单元数为4,系统参数如下。
1) MMC系统参数:SN=50 MV·A,额定频率f1=f2=50 Hz,子模块电容C=3 300 μF,直流侧电压Vdc/2=30 kV,桥臂串联电抗l=3 mH。
2) 交流系统参数:交流系统电压幅值VN= 138 kV,线路阻抗参数R=0.03 Ω,L=5 mH,采用换流变压器Yn/Δ接法,变压器额定功率为55 MV·A,漏抗标么值XT=0.05,两侧交流系统短路比为5;采样周期Ts=100 μs。
3.2 仿真结果
最初,海上风电传输MMC-HVDC系统处于稳定状态,40 MW的电能从交流系统1流向交流系统2。Vdcref=60 kV,所有的MMC单元在单位功率因数条件下运行,模型预测控制的环流抑制功能在初始状态是禁用的(即式(16)中的系数 )。在t为0.1 s和 0.4 s时,开启MMC单元的环流抑制功能(系数
)。在t为0.1 s和 0.4 s时,开启MMC单元的环流抑制功能(系数 ),仿真结果如图6和图7所示。
),仿真结果如图6和图7所示。
MMC1中的环流和A相上、下桥臂的电流图分别如图6(a)和6(b)所示。从图6(a)和6(b)可见:在t=0.1 s开启模型预测控制的环流抑制功能之后,环流和上下桥臂的电流显著减小,抑制效果明显。
图6(c)显示了MMC1设置在参考值(Vdc/4)时其子模块的电容电压,验证了所提出的模型预测控制策略对维持子模块电容电压在其额定值的有效性。从电容电压波形可以看出,子模块的电容电压纹波在t=0.1 s后显著减少,这是由于抑制了环流。
MMC1的交流输出相电流波形和交流输出线电压波形图分别如图6(d)和6(e)所示。从图6(d)和6(e)可见:当t=0.1 s时,由于环流的影响,子模块的电容电压纹波增加,导致交流侧电压和电流波形失真;在t=0.4 s开启模型预测控制功能后,改善了交流侧电压和电流的波形质量,得到了理想的波形。
在t=0.4 s开启环流抑制功能时,MMC2中相应的波形如图7所示。图7(a)~(e)所示图形分别与图6(a)~(e)所示波形有密切联系。
仿真图验证了所提出的模型预测控制策略抑制MMC单元环流的有效性,并实现MMC单元的电容电压均压,同时也反映了环流和电容电压不平衡对MMC单元的运行有不利影响,突出了环流抑制和电容电压平衡的重要性。

图6 MMC1中模型预测控制策略的仿真结果
Fig. 6 Simulation results of MMC1 with predictive control strategy

图7 MMC2中模型预测控制策略的仿真结果
Fig. 7 Simulation results of MMC2 with predictive control strategy
4 结论
1) 提出一种模型预测控制(MPC)策略用于海上风电的MMC-HVDC系统。在模型预测控制理论的基础上,根据MMC的离散时间数学模型,开发对应于离散时间模型的预测模型,并定义相对应的目标函数,通过求解这个目标函数的最优化问题,得到每个MMC单元中开关器件的最佳开关状态来抑制循环电流,并实现MMC单元的电容电压平衡。
2) 利用MATLAB/SIMULINK软件对五电平MMC-HVDC系统的进行仿真,结果证明了该模型预测控制策略的有效性和可行性。该策略可大大降低输出波形的畸变程度,使其更逼近正弦波;实现原理简单,非常适用于海上风电传输的MMC-HVDC系统。
参考文献:
[1] Noro Y, Arai J, Takagi K, et al. System study of direct current power transmission system connected to wind farm[C]// Transmission and Distribution Conference and Exhibition. Yokohama, Japan: IEEE, 2002: 944-949.
[2] 宋础, 刘汉中. 海上风力发电厂开发现状及发展趋势[J]. 上海电力, 2008, 2(1): 59-63.
SONG Chu, LIU Hanzhong. Development situation and trend of offshore wind farm[J]. Shanghai Electric Power, 2008, 2(1): 59-63.
[3] 王志新. 海上风力发电技术[M]. 北京: 机械工业出版社, 2012: 1-16.
WANG Zhixin. Offshore wind energy generation technology[M]. Beijing: China Machine Press, 2012: 1-16.
[4] Marquard T R, Lesnicar A. A new modular voltage source inverter topology[C/CD]//European Conference on Power Electronics and Applications. Toulouse, France: EPE, 2003: 72-75.
[5] 张振华, 江道灼. 基于模块化多电平变流器的STATCOM研究[J]. 电力自动化设备, 2012, 32(2): 62-66.
ZHANG Zhenhua, JIANG Daozhuo. STATCOM based on modularized multilevel converters[J]. Electric Power Automation Equipment, 2012, 32(2): 62-66.
[6] 何大清, 蔡旭. 模块化多电平变流器的限幅控制和混合调制[J]. 电力自动化设备, 2012, 32(4): 63-66.
HE Daqing, CAI Xu. Limitation control and hybrid modulation of modularized multilevel converter[J]. Electric Power Automation Equipment, 2012, 32(4): 63-66.
[7] Glinka M, Marquardt R. A new AC/AC multilevel converter family[J]. IEEE Transactions on Industrial Electronic, 2005, 52(3): 662-669.
[8] Allebrod S, HamerskI R, Marquardt R. New transformerless,scalable modular multilevel converters for HVDC-transmission[C]//Power Electronics Specialists Conference. Chicago, USA, 2008: 174-179.
[9] 屠卿瑞, 徐政, 郑翔, 等. 模块化多电平换流器型直流输电内部环流机理分析[J]. 高电压技术, 2010, 36(2): 547-552.
TU Qingrui, XU Zheng, ZHENG Xiang, et al. Mechanism analysis on the circulating current in modular multilevel converter based HVDC[J]. High Voltage Engineering, 2010, 36(2): 547-552.
[10] 丁冠军, 汤广福, 丁明, 等. 新型多电平电压源换流器模块的拓扑机制与调制策略[J]. 中国电机工程学报, 2009, 29(36): 1-6.
DING Guanjun, TANG Guangfu, DING Ming, et al. Topology mechanism and modulation scheme of a new multilevel voltage source converter modular[J]. Proceedings of the CSEE, 2009, 29(36): 1-6.
[11] Hagiwara M, Akagi H. Control and experiment of pulse width-modulated modular multilever converters[J]. IEEE Trans on Power Electronics, 2009, 24(7): 1737-1746.
[12] 梁帅奇, 牟晓春, 赵雪, 等. 含有储能单元的微电网运行控制技术[J]. 电力科学与技术学报, 2011, 26(4): 74-79.
LIANG Shuaiqi, MOU Xiaochun, ZHAO Xue, et al. Operation and control techniques of micro-grids with energy storage[J]. Journal of Electric Power Science and Technology, 2011, 26(4): 74-79.
[13] Hagiwara M, Maeda R, Akagi H. Control and analysis of the modular multilevel cascade converter based on double-star chopper-cells(MMCC-DSCC)[J]. IEEE Transactions on Power Electronics, 2011, 26(6): 1649-1658.
[14] Hagiwara M, Maeda R, Akagi H. Negative-sequence reactive-power control by the modular multilevel cascade converter based on double-star chopper-cells (MMCC- DSCC)[C]//IEEE Energy Conversion Congress and Exposition (ECCE). Atlanta, USA: IEEE, 2010: 3949-3954.
[15] Marquardt R, Lesnicar A, Hildinger J.Modulares stromrichterkonzept for netzkupplung san-wendung bei hohen spannungen[C]//Proceeding of ETG-Fachtagung. Bad Nauheim, Germany: IEEE, 2002: 1-7.
[16] Qin J, Saeedifard M. Predictive control of a modular multilevel converter for a back-to-back HVDC system[J]. IEEE Transactions on Power Delivery, 2012, 27(3): 1538-1547.
[17] Cortes P, Kouro R, Rocca B L, et al. Guidelines for weighting factors design in model predictive control of power converters and drives[C]//IEEE International Conference on Industrial Technology. Gippsland, Australia: IEEE, 2009: 1-7.
(编辑 陈灿华)
收稿日期:2014-10-10;修回日期:2014-12-23
基金项目(Foundation item):国家自然科学基金资助项目(51207048);湖南省科技计划项目(2014GK3006);长沙市科技计划项目(K1501012-11)(Project (51207048) supported by the National Natural Science Foundation of China; Project (2014GK3006) supported by Hunan Science and Technology Program; Project (K1501012-11) supported by Changsha Science and Technology Program)
通信作者:夏向阳,博士,教授,从事电力电子技术在电力系统的应用研究;E-mail:xia_xy@126.com