J. Cent. South Univ. (2012) 19: 1832-1838
DOI: 10.1007/s11771-012-1216-x
Trispectrum and correlation dimension analysis of magnetorheological damper in vibration screen
WU Fu-sen(吴福森), HUANG Yi-jian(黄宜坚), HUANG Kai(黄凯), XU Shan(徐姗)
College of Mechanical Engineering and Automation, Huaqiao University, Xiamen 361021, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: In order to improve the screening efficiency of vibrating screen and make vibration process smooth, a new type of magnetorheological (MR) damper was proposed. The signals of displacement in the vibration process during the test were collected. The trispectrum model of autoregressive (AR) time series was built and the correlation dimension was used to quantify the fractal characteristics during the vibration process. The result shows that, in different working conditions, trispectrum slices are applied to obtaining the information of non-Gaussian, nonlinear amplitude-frequency characteristics of the signal. Besides, there is correlation between the correlation dimension of vibration signal and trispectrum slices, which is very important to select the optimum working parameters of the MR damper and vibrating screen. And in the experimental conditions, it is found that when the working current of MR damper is 2 A and the rotation speed of vibration motor is 800 r/min, the vibration screen reaches its maximum screening efficiency.
Key words: screening efficiency; vibration screen; magnetorheological (MR) damper; autoregressive (AR) time series; trispectrum slices; correlation dimension
1 Introduction
Magneto-rheological fluid (MRF) [1] is a smart soft-matter. It can reversibly transform from Newtonian fluid into viscoplastic fluid with controllable yield strength in milliseconds when exposing to a magnetic field. MRF has wide application because it has many advantages such as higher strength, lower viscosity, consuming fewer energy and being insensitive to impurity [2]. A main application area for MR fluids is in dampers mounted in semi-active or adaptive vibration control, which have attracted a great deal of attention in recent years. YANG [3] developed a fundamental understanding of large-scale MR dampers for the purpose of designing and implementing these “smart” damping devices in large-scale structures. XIA [4] presented an inverse model of the MR damper, and the model can predict the required voltage accurately so that the MR damper can produce the desired force to meet the requirement of vibration control of structures.
Vibration screen has combined the theory of probability sieve with the engineering practice successfully. It is an important unit operation for the separation of particles according to their sizes. Presently, the probability screen is widely used in industries ranging from the traditional mineral and metallurgical sectors to the contemporary fast-growing food and pharmaceutical engineering [5]. But both the vibration absorbing and noise reduction are the problems to be badly solved in the practical operation of vibrating screen [6].
Higher order spectrum (HOS) is the multi- dimensional Fourier transform of higher order cumulant. It can restrain the additive white noise because it is insensitive to the Gaussian noise [7]. The amplitude and phase of the signals can be reconstructed by using the higher order spectrum. Trispectrum [8] is a kind of HOS with fourth-order cumulant. For the high estimation accuracy of its slices, trispectrum is conductive to extract the nonlinear coupling characteristics of vibration signal.
Correlation dimension can extract and recover natural law [9] of vibration system from a component of the time series. And the GP algorithm [10] used to solve correlation dimension is simple and reliable. Therefore, we can calculate correlation dimension as fractal dimension, then reconstruct the dynamic characteristics of the system.
The MR damper is applied to vibration system of vibration screen. Displacement signals are collected in vibration process. And inherent characteristic information of vibration system can be extracted with the unique advantages of the combination of trispectrum and correlation dimension. Then, the impact of different working parameters on the vibration system is analyzed. The estimation model of MR damper and vibration screen operating parameters can be established based on trispectrum-correlation dimension.
2 AR trispectrum model
Assume that the non-Gaussian zero-mean white noise a(t), which is contained in the output displacement signals, is the input of the process; y(t) is the additive white Gaussian noise. The AR model responding to an autoregressive process can be written as [11]
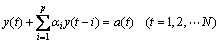 (1)
(1)
where αi(i=1, 2,…, p) denotes AR coefficient, and p is the order of AR model.
The high order cumulant of a(t) can be expressed with γa,n:
 (2)
(2)
where τ1, τ2,…, τn-1 are delays. Assume that τ1=τ2=…=τn-1=0. From Eq.(2), we can obtain:
 (3)
(3)
Then, define S=γa,3/(γa,2)3/2 and K=γa,4/(γa,2)2 as skewness and kurtosis [12], respectively. Assume that delay is given as i0=i1-τ1=i2-τ2=…=in-1-τn-1=i, then the high order cumulant of system output y(t) can be expressed as
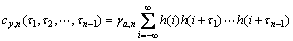 (4)
(4)
On the assumption, time series have additive n-th order cumulant cy,n(τ1, τ2, …, τn-1). Then, define the (n-1) dimensional Fourier transform as the n-th order spectrum. It can be denoted as
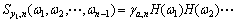
 (5)
(5)
where ω is frequency, H(ω) is the systemic transfer function, H*(ω) is the conjugate function of H(ω). Specially, when n=4, Eq. (5) becomes trispectrum TAR(ω1, ω2, ω3):
TAR(ω1, ω2, ω3)=γa,4H(ω1)H(ω2)H(ω3)H*(ω1, ω2, ω3) (6)
The amplitude of AR trispectrum can be obtained:
 (7)
(7)
When freezing one frequency of AR trispectrum TAR(ω1, ω2, ω3), ω3=C1(const), the expression formula of 2-D slices of AR trispectrum can be defined by
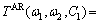
 (8)
(8)
The amplitude is
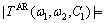
 (9)
(9)
When ω1=ω2=ω3=C2(const), the expression formula of E-F slices is given as follows:
 (10)
(10)
The amplitude is
 (11)
(11)
3 Calculation of correlation dimension
Correlation dimension can be obtained by calculating the dynamical system attractor dimension of one-dimensional time series. This method is called GP algorithm.
To reconstruct phase space of time series, assume that {XK} is the observed time series, K=1,2,…N:
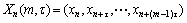 (12)
(12)
where n=1, 2, …, N-m+1, τ=K?t is time-delay, ?t is data sampling interval, K is any integer, and m is embedding dimension of phase space. So, the correlation dimension of strange attractor in reconstructed phase space is
 (13)
(13)
where C(r) is coherently integral used in vibration signal:
 (14)
(14)
and r is m-dimensional sphere radius. H is called Heaviside function:
 (15)
(15)
Delay parameter τ and embedding dimension m are two important parameters in the process of solving correlation dimension. ADD (Across Displacement) [13] cross-displacement method is used to determine the delay parameter τ; Improved-FNN method (improved false nearest point method) [14] is used to obtain the minimum embedding dimension m. The method of wavelet decomposition and reconstruction which are used in original vibration signal processing can solve the correlation dimension fluctuation problems in actual solving process, meanwhile, the noise impact on correlation dimension of the system can be eliminated. So, the calculated correlation dimension is more reliable.
4 Test
4.1 Test equipment
MR damper was developed for screening test in GLS10 vibration screen. Table 1 lists the technical parameters.
Table 1 Technical parameters of GLS10 vibration screen

All MR dampers used in test and engineering are independently researched and developed. The MRF used in test and engineering are prepared, which has viscosity of 0.2-0.3 Pa·s, density of 1-3 g/cm3, operating temperature from 35 to 150 °C. Damping force can be continuously adjusted in the load range by changing the voltage and current value of the damper. Therefore, the semi-active control of vibration system can be achieved. Table 2 lists the technical parameters of MR damper.
Table 2 Technical parameters of MR damper

Figure 1 (a) shows the vibration screen tester, and Fig. 1(b) shows the MR damper.

Fig. 1 MR damper testing in vibration screen: (a) Tester; (b) MR damper
4.2 Signal acquisition
The equipments that are used to collect the displacement signals in the direction of vibration consist of hardware and software. The module control unit of hardware is a kit of PXI-8195RT signal collecting instrument, which is produced by the National Instruments (NI). In addition, there is a GPS-3030D DC electrical source, a ST-1-03 eddy-current transducer with a resolution of 0.1×10-4.
According to the parameters of the actual work requirements, three groups of motor speed are selected: 700, 800 and 900 r/min. And each group is divided by current into four groups: 0, 1, 2 and 3 A.
5 Analysis
5.1 Trispectrum
The major problem about the calculation of trispectrum is how to display it. Due to having three frequency variables, the amplitude of trispectrum requires four-dimensional space to display, which is depicted in Fig. 2(a). Here, an overall picture of the phase space to display the magnitude of the entire trispectrum is given. To achieve this, a sphere is drawn at each point in the phase space in Fig. 2(b). The size and shade of the sphere represent the magnitude of that point: large dark points represent high magnitude, and smaller light points represent low magnitude [15].
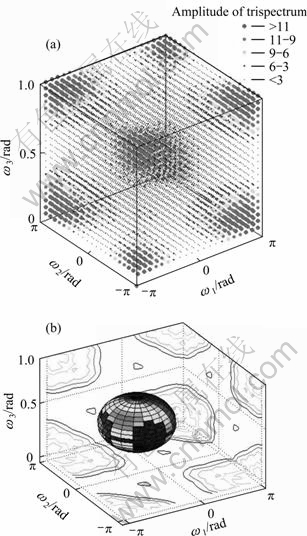
Fig. 2 Phase space (a) and contour map (b)
5.2 Two dimensional slices of trispectrum (2-D slices)
In order to accurately select the optimal operating parameters, firstly, the sampled data of various operating currents at each speed were analyzed and bispectra through their trispectra were reconstructed. Figure 3 shows 2-D slices, when the applied motor speed is 700, 800 and 900 r/min. These slices indicate the effect of phase coupling of different input signals. Overall, with the speed increasing, spectrum peak gradually changes from deconcentration to concentration. This shows that, the higher the motor speed is, the more the excitation frequency deviates from the natural frequency of vibration screen. The distribution of peaks accurately reflects the vibration dynamics of the system itself. From the speed point, compared with n=800 r/min, when the speed is 700 r/min or 900 r/min, spectrum shape is relatively thick, and spectral peaks also have a relatively dispersed distribution. From the current perspective, no matter what the speed is, there are concentrated peaks where current is 1 A or 2 A. Especially, when n=700 r/min, I=1 A or 2A, the distribution of peak on the frequency domain surface is more concentrated, and there are not too many clusters around the peak.
According to the observation of 2-D trispectrum slices, it can be found that, when n=800 r/min, and I=1 A or 2 A, MR damper performance emerges better variable, and also the coordination and stability of vibration system are better.
5.3 Equal frequency slices (E-F slices)
Figure 4 shows the trispectrum of E-F slices, as well as further analysis and comparison in working condition of I=1 A and 2 A.
The information of phase coupling shown in Fig. 4 is much clearer than that in Fig. 3. Obviously, E-F slices show more information of signal’s nonlinear, non-Gaussian characteristics than 2-D slices. In Fig. 4(a), there is a baseband at ωa=±0.5π and ωb=±0.3π, when I=1 A, 2 A and n=700 r/min. In Fig. 4(b), ωc=(ωa- ωb)/2=±0.1π is a new frequency generating from beat frequency of baseband, which is called phase coupling. ±0.1π is the characteristic frequency which plays a leading role when the damper works. Characteristic frequency ωc gradually replaces the role of fundamental frequencies ωa and ωb, contributing almost all the energy of vibration system. In Fig. 4(c), when n=900 r/min, peaks at ±0.5π become very large again. At the same time, the peaks at ±0.3π move to ±0.25π.
Now, it can be clearly confirmed that, when n=800 r/min, the peak is more concentrated than that at other speeds. And also, the peak is more concentrated at I=2 A than I=1 A. This further validates that MR damper has better damping effect with the operating parameters of n=800 r/min and I=2 A.
5.4 Correlation dimension analysis
The sampled data with various operating parameters were analyzed by the fractal approach and correlation dimension (D) calculation. Kurtosis (K) and skewness (S) are both the important parameters on describing situation of steepness and symmetry in peak distribution. The curves in Fig. 5(a) show the relationship of correlation dimension (D) and working current (I), and Fig. 5(b) shows the D-N curves of correlation dimension at each working speed (N) when I=2 A. In Fig. 5(c), K-S-D curves show the relationship among kurtosis, skewness and correlation dimension.
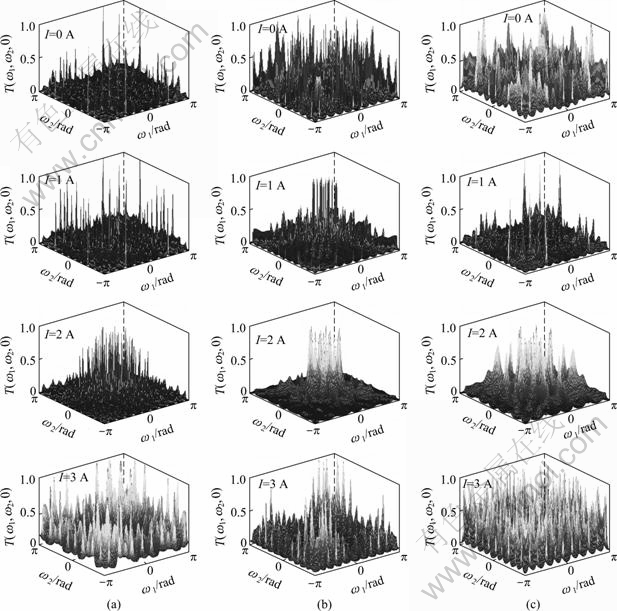
Fig. 3 2-D slices: (a) n=700 r/min; (b) n=800 r/min; (c) n=900 r/min
Figure 5(a) shows that correlation dimension D increases with motor speed and current. Curves of correlation dimension appear a turning point when I=2 A at each speed. Correlation dimension becomes larger abruptly, because high current makes damper stiffness too large, and also increases system noise. When n= 900 r/min, vibration signal has higher correlation dimension, and this is because high-frequency vibration makes frequency signal of damper covered by the noise signal. When n=700 r/min, current has little effect on the correlation dimension. Therefore, from the perspective of correlation dimension, n=800 r/min and I=1.5 A are the optimal combinations of parameters.
Figure 5(b) shows that correlation dimension curve occurs turning point at I=2 A and n=800 r/min. And when the speed reaches 900 r/min, correlation dimension increases sharply because of system noise. This also explains that MR damper achieves the optimal working state when n=800 r/min and I=2 A.
The K-S-D curve shown in Fig. 5(c) describes the variation within correlation dimension of vibration signal and peak distribution of trispectrum slices. Both kurtosis and skewness curves occur turning points at D=2.3, and there is no large fluctuations in following range of correlation dimension. This confirms, with the work parameters of n=800 r/min and I=2 A, MR damper does have the best damping performance. That makes vibration screen achieve the best working condition.
So, kurtosis and skewness of trispectrum and correlation dimension can be used as the characteristic quantities to identify damping effect of MR damper. And the parameter estimation model can be established after experiment.
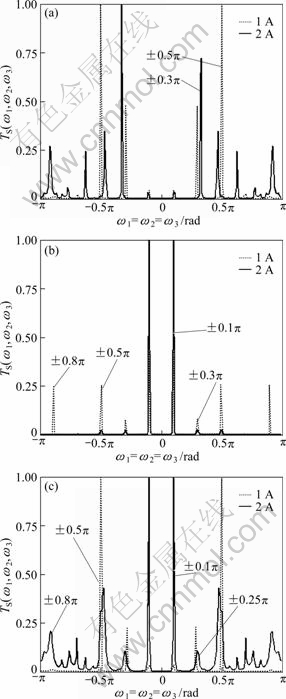
Fig. 4 E-F slices: (a) n=700 r/min; (b) n=800 r/min; (c) n=900 r/min
5.5 Screening efficiency analysis
Figure 6 shows the efficiency-current curve of screening test of vibration screen. Obviously, when the current of MR damper is 2 A and rotation speed of vibration motor is 800 r/min, the screening efficiency can reach 92.7%, which is much higher than that in other working conditions. The result is consistent with the analysis of Figs. 3, 4 and 5.
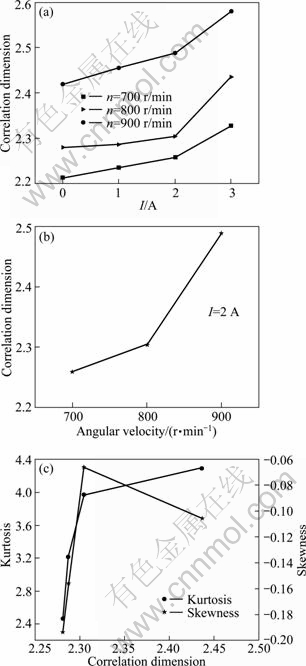
Fig. 5 Correlation dimension curves: (a) D-I curve; (b) D-N curve; (c) K-S-D curve
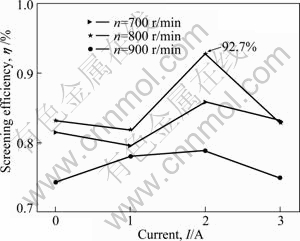
Fig. 6 Efficiency-current curve
6 Conclusions
1) When the working current is 2 A and the rotation speed of vibration motor is 800 r/min, the MR damper has the best working performance, and the vibration screen has the maximum screening efficiency.
2) When the vibration system is interfered with a zero mean and non-Gaussian white noise, AR model of fourth-order cumulant is established, and the higher order spectrum can be used to investigate the dynamic characteristics of MR damper.
3) Trispectrum slices can dispose the non-Gaussian, nonlinear coupling information of vibration signals quite well, which can reflect the dynamic characteristics of the MR damper in different working conditions.
4) Correlation dimension can reflect the internal rules of vibration signal. It is reliable to analyze the stability of vibration system in vibration screen and select the optimum working parameters of the MR damper.
References
[1] SOHAMED J, CETTEY A, MARWALA N. A magnetorheological actuation system: Test and model [J]. Smart Material and Structure, 2008, 17: 1-15.
[2] YING Z G, NI Y Q, KO J. Semi-active optimal control of linearized systems with multidegree of freedom and application [J]. Journal of Sound and Vibration, 2005, 279(1/2): 373-388.
[3] YANG G Q. Large-scale magnetorheological fluid damper for vibration mitigation: Modeling, testing and control [D]. Indiana: University of Notre Dame, 2001.
[4] XIA Pin-qi. An inverse model of MR damper using optimal neural network and system identification [J]. Journal of Sound and Vibration, 2003, 266(5): 1009-1023.
[5] KORDONSKI W I, SHOREY A B. Magnetorheological (MR) jet finishing technology [J]. Journal of International Material Systems and Structures, 2007, 18(12): 1127-1130.
[6] YARWALA D S, RILAKAZI B. Noise and vibration reduction of a vibrating screen [C]// 2005 SME Annual Meeting. Got Mining Preprints: SAM, 2005: 519-531.
[7] SCHURTER K C, ROSCHKE P N. Fuzzy modeling of a magnetorheological damper using ANFIS [C]// The 9th IEEE International Conference on Meeting. Xiamen, China: FUZZ IEEE, 2000: 122-127.
[8] BERGER B S, BETAI C, ANAND D K. time series analysis with auto regressive SVD algorithms [C]// The 37th Heat Transfer and Fluid Mechanics Institute. Sacramento: CSUS, 2001: 1-13.
[9] KYUNG J, JONGWON S, BYUNG M. A behavioral model of axisymmetrically configured magnetorheological fluid using Lekner summation [J]. Journal of Applied Physics, 2009, 105(7): 1-3.
[10] BALAN C, DIANA B, GHEORGHIU E. Rheological characterization of complex fluids in electro-magnetic fields [J]. Non-Newtonian Fluid Mech, 2008, 154: 22-30.
[11] YANG Shu-zi, WU Ya. Time series analysis in engineering application [M]. Wuhan: Huazhong University of Science and Technology Press, 2007: 181-187. (in Chinese)
[12] KHASHABA U A, SELMY A I. Prediction of surface roughness profiles for milled surfaces using an artificial neural network and fractal geometry approach [J]. Journal of Materials Processing Technology, 2008, 200(3): 271-278.
[13] ODIBAT Z, MOMANI S. Numerical methods for nonlinear partial differential equations of fractional order [J]. Applied Mathematical Modelling, 2008, 32(1): 28-39.
[14] DAVIS G B, KOHANDEL M. The constitutive properties of the brain paraenchyma. Part 2. Fractional derivative approach [J]. Medical Engineering and Physics, 2006, 28(5): 455-459.
[15] CHEN Bing-san, HUANG Yi-jian. Autoregressive trispectrum and its slices analysis of magnetorheological damping device [J]. Journal of Central South University of Technology, 2008, 15(s1): 247-251.
(Edited by YANG Bing)
Foundation item: Project(50975098) supported by the National Natural Science Foundation of China; Project(2008HZ0002-1) supported by the Major Scientific and Technological Program of Fujian Province, China
Received date: 2011-04-14; Accepted date: 2011-07-18
Corresponding author: HUANG Yi-jian, Professor; Tel: +86-13505026048; E-mail: yjhuang@hqu.edu.cn