Trans. Nonferrous Met. Soc. China 22(2012) 3087-3094
Three-dimensional analytical solution of acoustic emission or microseismic source location under cube monitoring network
DONG Long-jun, LI Xi-bing
School of Resources and Safety Engineering, Central South University, Changsha 410083, China
Received 11 May 2012; accepted 18 August 2012
Abstract: To find the analytical solution of the acoustic emission/microseismic(AE/MS) source location coordinates, the sensor location coordinates were optimized and simplified. A cube monitoring network of sensor location was selected, and the AE/MS source localization equations were established. A location method with P-wave velocity by analytical solutions (P-VAS) was obtained with these equations. The virtual location tests show that the relocation results of analytical method are fully consistent with the actual coordinates for events both inside and outside the monitoring network; whereas the location error of traditional time difference method is between 0.01 and 0.03 m for events inside the sensor array, and the location errors are larger, which is up to 1080986 m for events outside the sensor array. The broken pencil location tests were carried out in the cross section of 100 mm×98 mm, 350 mm-length granite rock specimen using five AE sensors. Five AE sources were relocated with the conventional method and the P-VAS method. For the four events outside monitoring network, the positioning accuracy by P-VAS method is higher than that by the traditional method, and the location accuracy of the larger one can be increased by 17.61 mm. The results of both virtual and broken pencil location tests show that the proposed analytical solution is effective to improve the positioning accuracy. It can locate the coordinates of AE/MS source only using simple four arithmetic operations, without determining the fitting initial value and iterative calculation, which can be solved by a conventional calculator or Microsoft Excel.
Key words: acoustic emission; seismic source; sensor; location; analytical solution
1 Introduction
It is generally accepted that most solids emit low-level seismic signals when they are stressed or deformed. Figure 1 shows the schematic classification of various kinds of events which generate seismic waves. In the geotechnical field, this phenomenon is generally referred to as acoustic emission/microseismic (AE/MS) activities [1,2]. When rock fractures, it produces AE/MS signals transmission through the rock as elastic waves [3,4]. The application of the AE/MS system, which monitors the self-generated acoustic signals occurring within the ground, has now rapidly increased for monitoring of underground structures such as mines, tunnels, natural gas, and petroleum storage caverns, as well as surface structures such as foundations, rock, and soil slopes [5,6].
The location of a seismic event (earthquake, MS or AE) is the first and most basic step in any study of seismicity at any scale since 1910 [7]. In general, earthquakes are solved for their source locations, defined by the coordinates and the origin time, assuming a seismic velocity model and minimizing the difference between the observed and the calculated travel times. Source location is one of the classic problems in seismic areas. A considerable number of studies published in the last more than 100 years on seismic source location prove the importance and, at the same time, the complexity of this problem [8].
Many researchers have developed different AE/MS/seismic source location techniques, some of which were mature and widely used in the positioning of AE or seismic source currently, for example, the Joint Hypocenter Determination method [9,10], the double difference method [11], master event relocation method [12] and topographic inverse [13]. Nevertheless, the problem of determining the four source parameters (geocentric: x, y, z and origin time) can still not be considered to be definitively solved. The iterative analytic procedures, which are nowadays most often used for the calculation (cf. Geiger’s method), are not infrequently divergent, or at any rate do not give very reliable results. This can lead to negative consequences when interpreting the activity itself. It is well-known that the correct location of the source is dramatically hindered by the following factors: 1) insufficient knowledge of the seismic wave velocity; 2) inadequate distribution of the stations; and 3) the intrinsic limitations of the iteration algorithm applied. Generally, those factors do not act independently each other [14]. Taking Geiger’s algorithm which is actually the most used and known one as an example, the use of initial evaluated hypocenter coordinates is presupposed, and an iterative least-squares technique is used. These conditions significantly influence the location accuracy [15].
To find the analytical solution of the AE/MS source location coordinates, the sensor location coordinates were optimized and simplified. A cube monitoring network of sensor location was selected, and the acoustic emission source or seismic source localization equations were established. A set of analytical solutions were obtained. Since, the proposed method is non-iterative, there is no convergence problem. The proposed algorithm is based only on acoustic measurements and does not need any electrical measurements, hence can be applied directly for online and real-time application. It requires only five sensors and some simple mathematical calculation. This method highlights two outstanding advantages: 1) without using iterative solution; 2) without initial evaluated hypocenter coordinates.
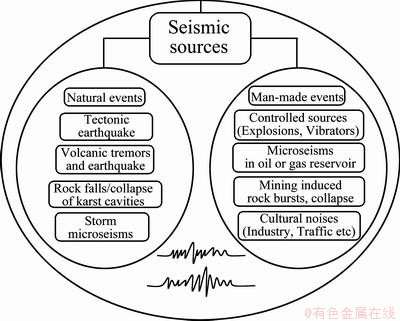
Fig. 1 Schematic classification of various kinds of events which generate seismic waves
2 Three-dimensional analytical solution of AE/MS source
The AE/MS/seismic source location method using P wave trigger time is widely used to calculate the source coordinates for two reasons: the fastest propagation velocity of the P wave, and the easy identification of that first trigger time. By positioning using this method, the P-wave velocity is known, and at least four or more different location monitoring stations are needed. Assume that the medium is homogeneous between each station (i.e. a uniform velocity model), and the P wave propagation speed is a constant value v; the AE/MS/seismic source location coordinate is (x0, y0, z0); Ti(i=1, 2, …, n) is the i-th monitoring station, and its coordinate is (xi, yi, zi) (i=1, 2, …, n); li(i=1, 2, …, n) is the distance from the AE/MS/seismic source to the station Ti; ti(i=1, 2, …, n) is the trigger time recorded by sensor in the station Ti; and t0 is the origin time of acoustic emission or seismic source. Then ti can be expressed as
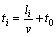 (1)
(1)
By the spatial distance formula between two points (the source location and the monitoring station location), one can obtain
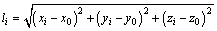 (2)
(2)
By taking Eq. (2) into Eq. (1), it becomes
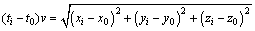 (3)
(3)
In Eq. (3), ti(i=1, 2,…, n), v, and (xi, yi, zi) (i=1, 2, …, n) are known; the seismic or AE source (x0, y0, z0) and origin time t0 are unknown, which need to be solved.
By taking each station datum to Eq. (3), an equation can be obtained; 4 stations correspond to 4 equations, and they can constitute a set of nonlinear equations. Generally, the more the number of station is, the higher the positioning accuracy is. In the past more than 100 years, most work was focused on nonlinear optimization or iteration methods to locate the AE/MS/seismic source. The location precision is greatly influenced by the error of sonic velocity and the intrinsic limitations of the iteration algorithm applied. In this work, in order to find out the analytical solution of the AE/MS/seismic source location coordinates, the sensor location coordinates were optimized and simplified.
A cube monitoring network of sensor location was selected, and the AE/MS/seismic source localization equations were established. The sensors were required to install at the vertices of the cube monitoring network; 4 sensors were installed in a face and additionally one sensor in another face, as shown in Fig. 2. For every face, there are four types of monitoring network including (a), (b), (c) and (d). The first type (a) is analyzed in this work, and the others are the same. Five sensors were installed at the vertices A, B, C, D and E of the cube monitoring network. The center of the cube is taken as the coordinate origin, and the coordinate direction is shown in Fig. 2.
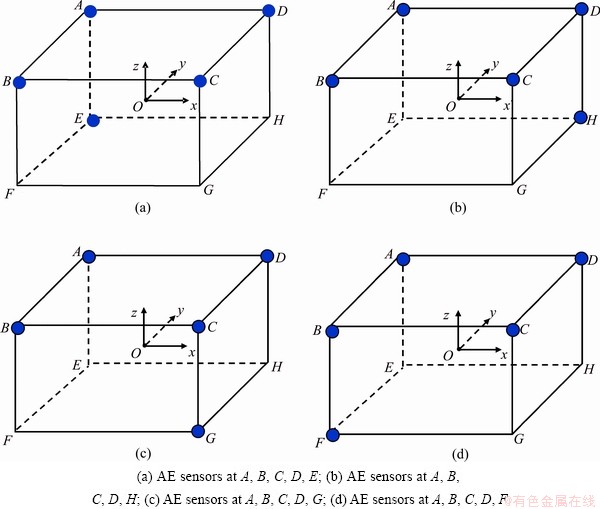
Fig. 2 Schematic of three-dimensional location of cube monitoring network
The lengths of three sides of the monitoring network cube are 2a, 2b and 2c. The first sensor A is taken as a reference. The travel time of the sensor A from an AE/MS/seismic event is expressed as t10, and the trigger time of sensor B, C, D and E are t10+Δt2, t10+Δt3, t10+Δt4 and t10+Δt5, respectively. According to Eq. (3), one can obtain
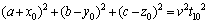 (4)
(4)
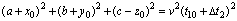 (5)
(5)
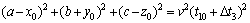 (6)
(6)
 (7)
(7)
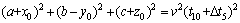 (8)
(8)
Equation (4) minus Eqs. (5), (6), (7) and (8), respectively, can be expressed as
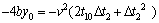 (9)
(9)
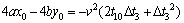 (10)
(10)
 (11)
(11)
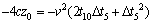 (12)
(12)
Equation (9) plus Eq. (11), and then their sum equals Eq. (10), and one can obtain
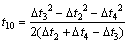 (13)
(13)
As the wave velocity v is known, y0, x0, and z0 are solved by Eqs. (9), (11) and (12), respectively, and are expressed as follows:
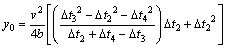 (14)
(14)
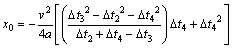 (15)
(15)
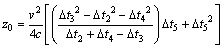 (16)
(16)
In Eqs. (14), (15) and (16), only x0, y0 and z0 are unknown, the others are known parameters, therefore, the exact analytical solution of the AE/MS/seismic source can be obtained by solving Eqs. (14), (15) and (16). The above method can be called location method with P-wave velocity by analytic solution (P-VAS).
3 Virtual position tests and analysis
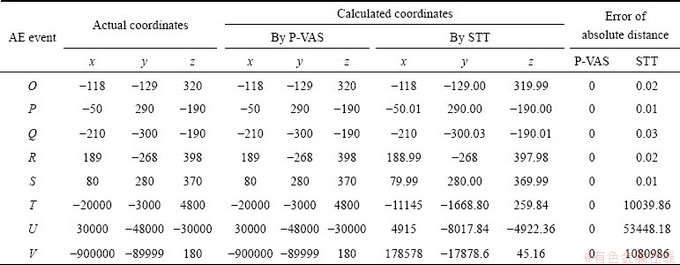
In virtual position tests, a positioning system includes 5 sensors at the 5 cube vertices, and the coordinates are A(-200, 300, 400), B(-200, -300, 400), C(200, -300, 400), D(200, 300, 400), E(-200, -300, -400), and the average equivalent P-wave velocity propagation in the medium is expressed as v, and v=5.2 m/ms. Assume that AE/MS sources O(-118, -129, 320), P(-50, 290, -190), Q(-210, -300, -190), R(189, -268, 398), and S(80, 280, 370) are in the sensor array; the sources T(-20000, -3000, 4800), U(30000, -48000, -30000), V(-900000, -89999, 180) are out of the sensor array (all coordinates are the length unit: m). The trigger times recorded by sensors are listed in Table 1. By using P-VAS method to calculate the AE/MS source coordinates, the coordinates of the five sensor values, velocity values and triggered time of 5 sensors for 8 events are taken into Eqs. (14), (15) and (16), and the coordinate values of eight acoustic emission events can be resolved. The calculated results are listed in Table 2. As can be seen from Table 2, the location results of P-VAS method are fully consistent with the actual coordinates for both inside and outside events of the monitoring network, and the accurate rate is 100%.
In order to compare with the existing positioning method, the traditional location method STT (Speed- trigger time) [16] was used to calculate the seismic or AE source coordinates, and the results are also listed in Table 2.
The location error of STT is between 0.01 and 0.03 m for events inside of the monitoring network, and the location errors are larger (the maximum can reach 1080986 m) for events outside of the monitoring network.
It is shown that the proposed P-VAS method is effective to improve the positioning accuracy, and especially for the events outside of the sensor array. The positioning accuracy is much higher than that of the traditional method STT. The analytical solution based on a cube monitoring network of sensor location can locate the coordinates of acoustic emission or seismic source only using simple four arithmetic operations, without determining the fitting initial value and iterative calculation. It can be solved with a conventional calculator or Microsoft Excel. The advantages of P-VAS can be summarized as follows: high precision, single solution, simple method, and convenient application.
Table 1 Trigger time recorded by sensors
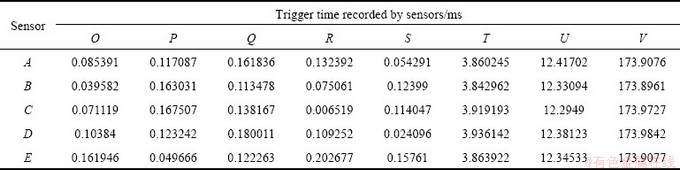
Table 2 Result comparison between P-VAS and STT (unit: m)
4 Broken pencil location tests in granite rock
4.1 Location tests
The tests were carried out in the cross section of 100 mm×98 mm, 350 mm-length rod of granite rock using five AE sensors. A broken pencil was simulated as an acoustic emission source in the rocks. Five AE sensors and PCI-2 based AE system of Physical Acoustics Corporation were used to record the trigger time and waveform data.
Five AE events include No.1, No.2, No.3, No.4 and No.5, and the corresponding coordinates are (-18, -24, 50), (-20, -49, 0), (20, -49, 0), (-100, 1, 50), and (-200, 0.5, 50), respectively. Five AE sensors are expressed as S1, S2, S3, S4 and S5, and arranged at the vertices A, B, C, D and E of the cube mmonitoring network, as shown in Fig. 2(a). Figure 3 shows the typical waves of AE events No.1. The trigger time recorded by AE sensors is listed in Table 3. Before positioning work, the wave velocity of various directions in the rock was tested. There are no obvious visible defects in the granite surface, but the velocities of different directions are obviously different, and the velocity interval is in the range of 2500 m/s-5400 m/s.
4.2 Results and analysis
Both STT and P-VAS methods were applied to relocate the acoustic emission source. The positioning velocity values were selected from 2500 m/s to the maximum value of 5400 m/s, and each solving location by additional 50 m. Some groups of the smaller errors of absolute distance were selected to compare the position accuracy of the two methods. Table 4 lists the average positioning coordinates and the average absolute distance error (AADE) of five acoustic emission events at different level of velocities using two methods. Figure 4 shows the absolute distance errors of 5 AE events positioning results of the two methods at different velocities.
Fig. 3 Typical waves of AE event No.1
Table 3 Trigger time recorded by AE sensors
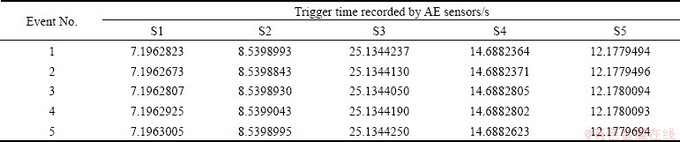
Table 4 Result comparison between P-VAS and STT (unit: mm)
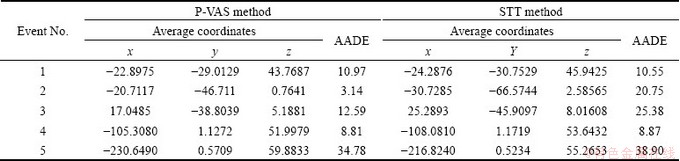
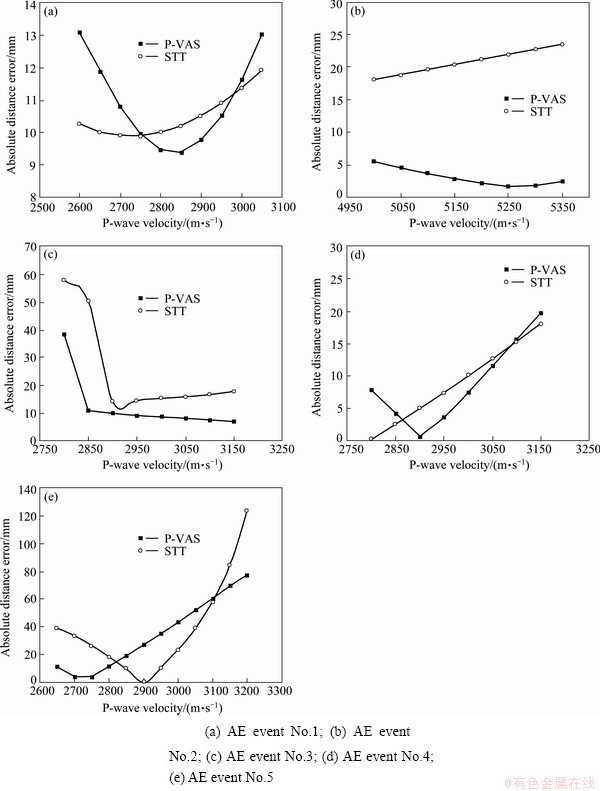
Fig. 4 Comparison of absolute distance errors at different velocities using P-VAS and STT methods
The results show that positioning accuracy has been markedly improved by using the analytical solution. The absolute distance errors of AE events No.1 and No. 4 are the same by the two methods. And the positioning accuracy of AE events Nos. 2, 3, and 5 are significantly improved. The larger one can be increased by 17.61 mm.
It can be seen from Fig. 4 that, the smallest points of absolute distance errors of five AE events can be found when using P-VAS method, however, only event Nos.4 and 5 have the smallest points when using STT method. It also shows that for the events Nos. 2, 3, 4 and 5, which are out of the cube of the monitoring network, the AADEs are lower by using P-VAS method. The results are consistent with that in virtual position tests in section 3.
The proposed P-VAS can locate the coordinates of AE/MS source only using simple four arithmetic operations, without determining the fitting initial value and iterative calculation, which can be solved by a conventional calculator or Microsoft Excel.
4.3 Discussion
The plane positioning accuracy is seriously influenced by the sonic speed, and the plane positioning error is larger than the line positioning error, which means that when the line position can satisfy the need in practical engineering, it is better to use the line position instead of the plane location [17]. There are three reasons as follows: the calculation of one-dimensional location is simple; the analytical solution of the location coordinate is easy to solve for any arbitrary distribution network. If a straight line of the wave propagation assumptions approximates reasonable, the analytical method can calculate the focal coordinates more accurately by the average velocity for heterogeneous medium.
The analytical solutions are very difficult to resolve. To solve the analytical solution in two-dimensional or three-dimensional location problem, the conditions of monitoring distribution network should be always pre-supposed. For example, this work is based on the analytical solution of the cube monitoring network. When z=0, then it becomes a two-dimensional positioning. In two-dimensional and three-dimensional location problems, the accurate coordinates can be obtained from the analytical solution for homogeneous media. However, for heterogeneous medium, the velocity field is very complex, even if the use of analytical location solution will produce larger error. For example, the MS monitoring in mining, gas and oil reservoir, the fact is that wave velocity is changed from time to time due to the continuous geological or man-made activity, and the accurate wave velocity cannot be estimated in advance; then, inaccurate wave velocity values seriously affect the positioning accuracy using already existing method. The proposed methods (TD) in Refs. [16,18] without using sonic speed can effectively decrease the positioning errors induced by velocity error, and can locate in real-time. Combined with TD and P-VAS methods [19], the coupled location method would have the advantages both of TD and P-VAS. Only the coordinates of the sensors and P wave arrival times are required to accurately solve the real-time source location parameters (including source coordinates, the source origin time and P wave velocity).
5 Conclusions
1) Based on the optimized and simplified coordinate of sensors, the AE source or seismic source localization equations were obtained, and a set of analytical solutions were developed under the cube monitoring network of sensor location.
2) Virtual source of the location tests and broken pencil location tests were carried out for verifying the proposed P-VAS method. And the STT methods were also applied to relocate the sources for comparing the location accuracy of two methods. The virtual location tests show that the relocation results of analytical method are fully consistent with the actual coordinates for events both inside and outside of the monitoring network; whereas the location error of traditional time difference method is between 0.01 and 0.03 m for events inside of the sensor array, and the location errors are larger, which reached 1080986 m for events outside of the sensor array. The broken pencil location tests were carried out in the cross section of 100 mm×98 mm, 350 mm-length granite rock specimen using five AE sensors. The five AE sources were relocated with the traditional method and the analytical method P-VAS. The positioning accuracy by P-VAS is higher than that by the traditional method for the four events outside of monitoring network, and the location accuracy of the larger one can be increased by 17.61 mm.
3) The proposed P-VAS method is effective to improve the positioning accuracy, and especially for the outside events of the sensor array. The positioning accuracy by P-VAS method is much higher than that by the traditional method. Based on a cube monitoring network of sensor location, the P-VAS method can locate the coordinates of AE/MS source only using simple four arithmetic operations, without determining the fitting initial value and iterative calculation. It can be solved by a conventional calculator or Microsoft Excel. The advantages of P-VAS are single solution, simple method and high precision.
References
[1] JONES G A, NIPPRESS S E J, RIETBROCK A, REYES- MONTES J M. Accurate location of synthetic acoustic emissions and location sensitivity to relocation methods, velocity perturbations, and seismic anisotropy [J]. Pure and Applied Geophysics, 2008, 165: 235-254.
[2] ZHOU Jian, LI Xi-bing, SHI Xiu-zhi, WEI Wei, WU Bang-biao. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2734-2743.
[3] LI Xi-bing, YAO Jin-rui, GONG Feng-qiang. Dynamic problems in deep exploitation of hard rock metal mines [J]. The Chinese Journal of Nonferrous Metals, 2011, 21(10): 2551-2563. (in Chinese)
[4] YIN Zhi-qiang, LI Xi-bing, JIN Jie-fang, HE Xian-qun, DU Kun. Failure characteristics of high stress rock induced by impact disturbance under confining pressure unloading [J]. Transactions of Nonferrous Metals Society of China, 2011, 22(1): 175-184.
[5] WANG Hong-liang, GE Mao-chen. Acoustic emission/microseismic source location analysis for a limestone mine exhibiting high horizontal stresses [J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45: 720-728.
[6] GE M. Source location error analysis and optimization methods [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2012, 4(1): 1-10.
[7] GEIGER L. Herdbestimmung bei erdbeben aus den ankunftszeiten, nachrichten von der  gesellschaft der wissenschaften zu
gesellschaft der wissenschaften zu  [J]. Mathematisch-Physikalische Klasse, 1910, 4: 331-349.
[J]. Mathematisch-Physikalische Klasse, 1910, 4: 331-349.
[8] PAUL G R, WALDHAUSER F, SCHAFF D, KIM W. The applicability of modern methods of earthquake location [J]. Pure Appl Geophys, 2006, 163: 351-372.
[9] PAVLIS G L. Appraising earthquake hypocenter location errors: A complete, practical approach for single-event locations [J]. Bull Seimol Soc Am, 1986, 76: 1699-1717.
[10] PAVLIS G, BOOKER J. Progressive multiple event location (PMEL) [J]. Bull Seismol Soc Am, 1983, 73: 1753-1777.
[11] WALDHAUSER F, ELLSWORTH W L. A double-difference earthquake location algorithm: Method and application to the northern hayward fault, California [J]. Bull Seism Soc Am, 2000, 90(6): 1353-1368.
[12] REYES-MONTES J M, RIETBROCK A, COLLINS D S, YOUNG R P. Relative location of excavation induced microseismicity at the underground research Laboratory (AECL Canada) using surveyed reference events [J]. Geophys Res Letts, 2005, 32: 1-4.
[13] HUSEN S, KISSLINGE, FLUEH E, ASCH, G. Accurate hypocentre determination in the seismogenic zone of the subducting Nazca Plate in northern Chile using combined on-/offshore network [J]. Geophys J Int, 1999, 138: 687-701.
[14] CACCAMO D, NERI G. A new analytic procedure to determine hypocentral parameters of local seismic events [J]. Bull Seism Soc Am, 1984, 74: 655-667.
[15] LI X B, DONG L J. Comparison of two methods in acoustic emission source location using four sensors without measuring sonic speed [J]. Sensor Letters, 2011, 9(5): 2025-2029.
[16] DONG Long-jun, LI Xi-bing, TANG Li-zhong, GONG Feng-qiang. Mathematical functions and parameters for microseismic source location without premeasuring speed [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2057-2067. (in Chinese)
[17] LI Qi-yue, DONG Long-jun, LI Xi-bing, YIN Zhi-qiang, LIU Xilin. Effects of sonic speed on location accuracy of acoustic emission source in rocks [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2719-2726.
[18] LI Xi-bing, DONG Long-jun, GONG Feng-qiang, ZHOU Zi-long. A location method for acoustic emission and microseismic sources: China, 201010600262.3 [P]. 2011-07-20. (in Chinese)
[19] DONG Long-jun, LI Xi-bing, GONG Feng-qiang. An analyticallocation method for acoustic emission and microseismic sources: China, 201110273728.8 [P]. 2012-05-02. (in Chinese).
一种立方体监测网络的声发射源和微震源解析定位方法
董陇军, 李夕兵
中南大学 资源与安全工程学院,长沙 410083
摘 要:通过选取合理的坐标原点及传感器位置简化声发射源定位方程, 得到声发射源或微震源三维定位方法的解析解。算例研究表明, 对于传感器阵列内、外的声发射源事件, 解析方法定位结果完全与实际坐标一致;对于传感器阵列内的声发射源事件, 传统方法略有误差, 一般为0.01-0.03 m, 而对于传感器阵列外的微震源, 传统时差定位方法的定位误差很大, 最大的达到1080986 m;采用横截面为100 mm×98 mm、长度为350 mm的花岗岩试样, 进行5次断铅定位实验, 分别用传统方法和解析方法进行定位, 结果发现在监测网络外的4个声发射事件, 解析定位的误差亦小于传统方法的定位误差。可见解析定位精度较传统方法有明显提高, 最高可提高17.61 mm;利用解析解定位, 无需确定拟合初值和拟合迭代算法, 仅通过简单的四则运算即可定位, 用常规的计算器或Microsoft Excel即可求解。
关键词:声发射;微震源;传感器;定位;解析解
(Edited by YUAN Sai-qian)
Foundation item: Project (10872218) supported by the National Natural Science Foundation of China; Project (2010CB732004) supported by the National Basic Research Program of China; Project (kjdb2010-6) supported by Doctoral Candidate Innovation Research Support Program of Science & Technology Review; Project (201105) supported by Scholarship Award for Excellent Doctoral Student of Ministry of Education of China
Corresponding author: DONG Long-jun; Tel: +86-18711191205; E-mail: csudlj@163.com
DOI: 10.1016/S1003-6326(11)61575-6