来流速度分布对径向热管换热器性能影响的数值模拟

涂福炳，马士伟，高晟扬，刘庆赟，毛建丰

(中南大学 能源科学与工程学院，湖南 长沙，410083)

摘要：利用FLUENT软件对径向热管换热器壳程进行数值计算，研究烟气入射角和速度均匀度对换热器流场、温度场和单位压降换热系数的影响规律。研究结果表明：当来流速度均匀时，入射角增大使热管背风侧回流区发生偏移，下游管束被上游管束尾迹覆盖，减少烟气与管束的碰撞，降低烟气压力损失，换热效率降低，在同一横截面上烟气温度分布较均匀；当来流速度不均匀时，换热器壳程烟气出现明显的高速区与低速区，使温度场均匀性变差，出现低温区，且不均匀因子τ越大，温度场均匀性越差，低温区范围也越大；单位压降换热系数α/△p随烟气入射角的增大而逐渐增大，在45°时达到最大值，此时换热器整体性能最好；此后，随入射角进一步增大，α/△p急剧减小，换热器性能恶化；当因子τ较小时，多股扰流能提高换热器整体性能，而少股扰流将降低换热器整体性能，且因子τ越大，换热器整体性能越差；壳程温度模拟结果与测试结果相比，相对误差在5%以内。

关键词：径向热管换热器；数值模拟；速度分布；入射角；单位压降换热系数；换热性能

中图分类号：TK172.4                 文献标志码：A         文章编号：1672-7207(2013)09-3904-07

Numerical simulation of radial heat pipe heat exchanger under different velocity distribution inflows

TU Fubing, MA Shiwei, GAO Shengyang, LIU Qingyun, MAO Jianfeng

(School of Energy Science and Engineering, Central South University, Changsha 410083, China)

Abstract: The characteristics of the flow field, temperature field and heat transfer coefficient of unit pressure drop were analyzed under different inclination angles and velocity evenness by simulating the shell side of a radical heat pipe heat exchanger with the software FLUENT. The results show that when the velocity inflows are evenly distributed, the inclination angles with increment cause the migration of the reflux zones behind the heat pipes and make the wake of the upper pipes cover the lower pipes, so the collision between the flue gas and the heat pipes abates, the pressure loss drops and the heat exchange rate decreases, while a uniform temperature reaches at the same cross section. When the velocity inflows are unevenly distributed, sensible high velocity zone and low velocity zone emerge in the shell side of the heat exchanger, the uniformity of temperature field becomes worse with low temperature zone, and the larger the unevenness factor τ is, the worse the uniformity of temperature field is, the larger the low temperature zone is. The heat transfer coefficient of unit pressure drop α/△p increases gradually as the inclination angle enlarges and culminates at 45° where the thermal performance of the heat exchanger gets its optimum, since then α/△p decreases rapidly and the thermal performance of the heat exchanger deteriorates remarkably. Inflows with more interference flows and smaller τ factor can improve the integrity performance of the heat exchanger, but inflows with less interference flows will decrease the integrity performance, and the larger the τ factor is, the more deterioration. The relative error of the temperature simulation results in the shell side to experimental results is less than 5%.

Key words: radial heat pipe heat exchanger; numerical simulation; velocity distribution; inclination angle; heat transfer coefficient of unit pressure drop; thermal performance

传统的管壳式换热器传热系数低、易结垢、易腐蚀、占地面积大且金属耗量大，已不能满足节能降耗和系统优化的要求。而径向热管换热器由于传热效率高、等温性好、压降小、结构简单、紧凑性好、抗露点腐蚀等优点而广受青睐^[1]，已广泛应用于工业余热的回收利用。Cotter^[2]于1965年提出热管理论后，热管的研究一直受到很大关注。Lee等^[3]通过实验研究了影响热管传热性能的各种内外因素；Peretz等^[4]从参变量的非线性特征出发，对热管换热器几何结构进行了优化；孙世梅等^[5-6]借助计算流体力学软件对径向热管换热器内流体的流动和传热进行了数值模拟研究；陈洁等^[7]以经济效益为目标函数对用于回收空调排风热量的热管换热器进行了研究，得到了不同温度下换热器的最优结构；许欣^[8]通过引入多孔介质模型和分布阻力方法，得到了径向热管换热器在来流速度均匀情况下压力分布特征以及压降公式。在此，本文作者应用数值模拟方法研究来流速度分布对换热器流场、温度场和整体性能的影响规律，以便为径向热管换热器工程应用提供参考。

1  模型的建立

1.1  物理模型

径向热管换热器几何结构和壳程流场比较复杂，为了得到研究对象的壳程流场和压力场，同时考虑到换热器壳程烟气流动的实际情况，对研究对象进行如下简化：(1) 不考虑烟气中烟尘颗粒的影响，将烟气视为多质单相流体；(2) 烟气物理性质稳定，不发生相变和化学变化等；(3) 将烟气视为各向同性、均匀连续性的不可压缩牛顿流体；(4) 将烟气流动视为稳态流动；(5) 不考虑热管污垢对换热的影响。热管换热器结构参数如表1 所示。

换热器计算区域如图1所示。考虑到热管的对称性，只需对1-1和2-2这2个对称面之间的区域进行模拟。对于换热器的网格划分，以径向热管单元为中心将模型划分成众多的小体，然后，对这些小体分别进行网格划分；利用六面体网格来划分径向热管单元及翅片部分，用三棱柱网格划分换热器壳程空间。图2所示为计算区域局部三维网格图。

1.2  数学模型

数学模型包括质量方程、动量方程、能量方程以及气体状态方程。这些模型是较普遍的计算模型，具体方程式见文献[9]。标准k-ε双方程湍流模型可用于壁面边界层、管流、无旋及弱旋的二维或三维流动、通道流等，在工程实际及科学研究中得到了广泛的应用。本文运用标准k-ε双方程模型的输运方程模拟径向热管换热器壳程烟气的流动。

表1  径向热管换热器的结构参数

Table1  Structural parameters of radial heat pipe heat exchanger

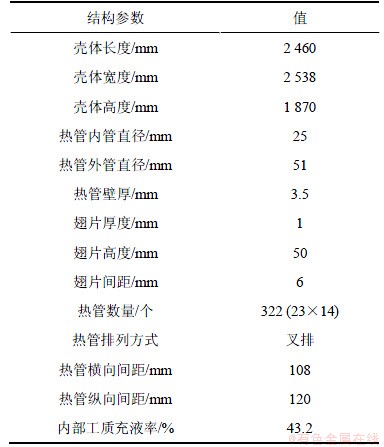
图1  换热器计算区域示意图

Fig.1  Schematic diagram of heat exchanger computational domain

图2  热管换热器局部三维网格图

Fig.2  Local three-dimensional mesh of radial heat pipe heat exchanger

1.3  模型设置求解及边界条件

采用稳态、定常模型和PRESTO压力插补格式；利用二阶迎风格式离散控制方程对流项；采用SIMPLE算法求解离散方程；采用标准壁面函数法处理近壁面烟气流动。

采用速度入口边界条件，以现场运行的径向热管换热器为研究对象。由于烟气进入换热器前在烟道中进行了转向，使得换热器入口速度分布比较复杂。通过对其流场进行模拟，可得到换热器入口烟气速度分布，速度拟合式为(不考虑烟气沿热管轴向流动)：

v_x =-0.494 6-45.371 3x+154.565 2x²-139.875 1x³+51.879 7x⁴-7.096 2x⁵，拟合度r=0.987 4    (1)

v_y =1.882 9-64.753 3x+84.351 9x²-40.805 6x³+6.811 9x⁴，拟合度r=0.972 8         (2)

入口烟气温度为185 ℃，流量为128 203 m³/h。烟气成分见表2。入口烟气湍流采用水力直径和湍流强度。

表2  烟气成分(体积分数)

Table2  Components of flue gas          %

出口边界采用自由流出口边界，近壁区采用壁面函数法处理。面1-1和2-2设置为对称边界；换热器壳侧壁面设置为无滑移、无渗透及绝热边界；热管内壁面设置为定温；外壁面设定为无滑移，无渗透；选择Coupled流固耦合条件。

采用等效导热系数法对热管工质相变过程进行简化^[10-11]。热管等效导热系数由下式^[12]计算：

         (3)

式中：为等效导热系数，W/(m·K)；R为充液率，%，文中取R=43.2%。

2  模型验证

换热器壳程不同点温度测试结果与模拟结果对比如表3所示。

表3中4个测点均布于热管换热器的中心线上。从表3可以看出：数值模拟结果与测试结果有相同的变化趋势，各测点温度相对误差小于5%，说明所建模型合理，结果可靠。

表3  壳程温度模拟结果与测试结果比较

Table 3  Comparison between simulation results and test results of temperature in shell side

3  来流速度分布对换热器性能影响的数值模拟

速度包含方向与大小2个特征，可以从入射角和均匀度2方面设计来流速度分布方案，模拟分析换热器性能变化情况，以便为改善换热器整体性能提供依据。

3.1  来流入射角方案

烟气入射角φ定义为：在X-Y平面内，烟气速度与竖直方向所成的角度。方案设计以换热器入口烟气质量流量不变为基础，且换热器入口处速度均匀，入射角方案如表4所示。

表4  烟气入射方案

Table 4  Schemes for smoke inclination angles

3.2  来流速度均匀度分布方案

在来流平均速度相等的基础上，引入速度不均匀因子τ衡量来流速度的不均匀程度，其定义式为^[13]

             (4)

式中：n为控制单元数；S为换热器迎风面面积，m²；S_i为换热器第i个单元迎风面面积，m²；v_i为第i个单元进口速度，m/s；为换热器入口截面平均速度，m/s。

在入射角为0°的前提下，选取3种典型的阶梯型即二阶阶梯型、三阶阶梯型和抛物阶梯型速度分布进行模拟计算，各阶梯型速度分布如表5所示。从表5可见：方案序号越大，速度分布越不均匀，因子τ越大；各阶梯型速度分布中的分速度在换热器入口X轴方向上的宽度相等。

3.3  模拟结果分析

3.3.1  对流场的影响

图3所示为来流速度均匀且入射角φ为0°时换热器壳程局部速度矢量图。由图3可知：换热器壳程流场较均匀，烟气流无明显偏移。前排管束的尾迹与单圆柱绕流的尾迹非常相似，在管束后形成稳定的楔形双涡旋回流区。沿烟气流向，由于管束的干扰，烟气流湍流度增加，热管背风侧产生涡脱落现象。

图4所示为来流速度均匀且入射角φ为45°时换热器壳程局部速度矢量图。由图4可知：由于烟气流斜向进入换热器，热管背风侧回流区发生偏移，下游管束被上游管束尾迹覆盖，出现类似于顺排管束的流动状态，减少了烟气与管束的碰撞以及烟气压力损失，换热效率有所下降；此外，在换热器入口左侧有一范围较小的烟气滞流区，且随来流速度的增大，滞流区范围增大。

表5  不同阶梯型速度分布

Table 5  Different step velocity distributions        m/s

图3  φ=0°, Z=1.75 mm且来流速度均匀时局部速度矢量图

Fig.3  Local velocity vectors with uniform velocity inflow when φ=0° and Z=1.75 mm

图4  φ=45°, Z=1.75 mm且来流速度均匀时局部速度矢量图

Fig.4  Local velocity vector with uniform velocity inflow when φ=45° and Z=1.75 mm

图5所示为方案4的三阶阶梯型速度分布中换热器壳程速度矢量图。由图5可知：由于来流速度分布不均匀，换热器壳程出现明显的高速区与低速区，且不均匀度越大，高速区与低速区越明显；在不同速度交界处，烟气由高速区向低速区偏移。烟气流的偏移使热管背风侧回流区发生偏移，同样出现类似于顺排管束的流动状态，且速度不均匀程度越大，烟气产生偏移范围越大；沿壳程流向，烟气偏移逐渐减弱，速度逐渐均匀；此外，烟气经过管束间隙时速度越大，管束的磨损、振动越严重，故应避免换热器入口局部速度过大的情况出现。

3.3.2  对温度场的影响

图6所示为来流速度均匀且入射角φ为0°时换热器壳程温度分布云图。由图6可知：当来流速度均匀时，不同位置的烟气经过每排管束的温降基本相同，烟气在同一横截面上温度较均匀；靠近换热器壳壁的烟气温度较高，这是换热器壳壁设置为绝热边界的缘故。

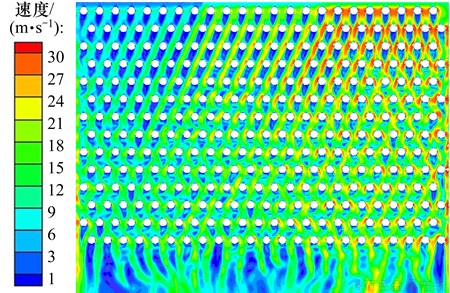
图5  φ=0°, Z=1.75 mm且来流速度为三阶阶梯型(方案4)时速度分布云图

Fig.5  Velocity profile with third-order type of velocity inflow for Scheme 4 when φ=0° and Z=1.75 mm

图6  φ=0°, Z=1.75 mm且来流速度均匀时温度分布云图

Fig.6  Temperature profile with uniform velocity inflow when φ=0° and Z=1.75 mm

图7所示为方案4的抛物阶梯型速度分布中换热器壳程温度分布云图。由图7可知：由于来流速度分布不均匀，换热器温度场均匀性变差，烟气在来流烟气速度小的区域停留时间较长，与管束换热时间也较长，出现低温区。在同一阶梯型分布中，因子τ越大，温度场均匀性越差，低温区范围也越大，此时，若低温区温度低于烟气露点，将使换热器产生局部腐蚀。

图7  φ=0°, Z=1.75 mm且来流速度为抛物阶梯型(方案4)时温度分布云图

Fig.7 Temperature profile with parabolic type of velocity inflow for Scheme 4 when φ=0° and Z=1.75 mm

3.3.3  对换热器整体性能的影响

在评价换热器整体性能时，换热量与压降往往是要兼顾的，有多种将换热量与压降结合的评价方法，如单位压降换热系数法、熵分析法、热经济学分析法等^[14]。实践证明：将单位压降换热系数α/△p作为衡量换热器综合性能的指标能获得理想效果^[15]；α/△p越大，表明换热器整体整体性能越好。

图8所示为α/△p 随入射角的变化情况。由图8可知：随着烟气入射角的增大，α/△p逐渐增大，并在入射角约为45°时达到最大，此时，换热器整体性能最好，提高幅度为2.31%；此后，α/△p随入射角的进一步增大急剧减小，换热器性能恶化。

图8  速度均匀时单位压降换热系数α/△p 随入射角变化情况

Fig.8  Relationship between α/△p and inclination angle when velocity inflow is uniform

当入射角为0°时，α/△p随τ因子的变化情况如图9所示。从图9可以看出：在二、三阶阶梯型下，随因子τ的增大，α/△p逐渐减小且下降幅度逐渐增大，换热器整体性能恶化；在抛物阶梯型下，α/△p随τ的增大先逐渐增大，并在τ为20%左右时达到最大；此后，随τ的继续增大，α/△p逐渐减小。经比较可知：二阶阶梯型速度分布下换热器性能恶化最严重，α/△p最大降幅为11.88%；其次是三阶阶梯型，最大降幅为5.14%；而抛物阶梯型在τ较小时提高了换热器整体性能。因此，当τ较小时，多股扰流能提高换热器整体性能；而少股扰流将削弱换热器整体性能，且τ越大，整体性能越差。

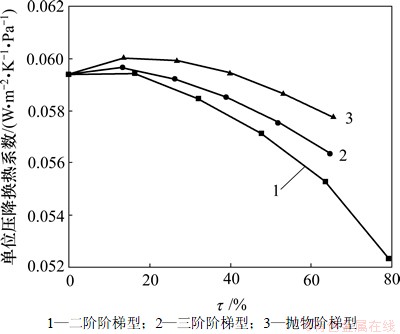
图9  入射角为0°时单位压降换热系数α/△p随不均匀因子τ变化情况

Fig.9  Relationship between α/△p and τ when inclination angle is 0°

4  结论

(1) 当来流速度均匀时，入射角增大使热管背风侧回流区发生偏移，下游管束被上游管束尾迹覆盖，减少了烟气与管束的碰撞，降低了烟气压力损失，换热效率有所降低；当来流速度分布不均匀时，换热器壳程烟气出现明显的高速区与低速区，烟气产生偏移，且不均匀度越大，高速区与低速区越明显，烟气偏移范围也越大。

(2) 当来流速度均匀时，同一横截面上烟气温度分布较均匀；当来流速度不均匀时，换热器温度场均匀性变差，来流速度小的区域烟气停留时间较长，与管束换热时间也较长，出现低温区，且因子τ越大，温度场均匀性越差，低温区范围也越大。

(3) 单位压降换热系数α/△p随烟气入射角的增大而逐渐增大，并在入射角为45°时达到最大，此时换热器整体性能最好。此后，α/△p随入射角的增大急剧减小，换热器性能恶化明显。

(4) 在τ较小时，多股扰流能提高换热器整体性能；而少股扰流将降低换热器整体性能，且烟气流不均匀度越大，整体性能恶化越严重。

参考文献：

[1] 毛建丰, 涂福炳, 许欣, 等. 同轴径向热管换热器壳程流场数值模拟[J]. 热科学与技术, 2010, 9(1): 31-35.

MAO Jianfeng, TU Fubing, XU Xin, et al. Numerical simulation on flow field of jacketed heat pipe heat exchanger[J]. Journal of Thermal Science and Technology, 2010, 9(1): 31-35.

[2] Cotter T P. Theory of heat pipes[R]. Los Alamos: Los Alamos Scientific Lab, 1965: 1-37.

[3] Lee Y, Mital U. A two-phase closed thermosyphon[J]. International Journal of Heat and Mass Transfer, 1972, 15(9): 1695-1707.

[4] Peretz R, Horbaniuc B. Optimal heat pipe heat exchanger design[J]. Journal of Heat Recovery Systems, 1984, 4(1): 9-24.

[5] 孙世梅, 张红. 热管换热器流动与传热的CFD模拟及试验[J]. 南京工业大学学报, 2004, 26(2): 62-66.

SUN Shimei, ZHANG Hong. Analysis of CFD simulation with experiment of heat transfer and pressure drop for heat pipe heat exchanger[J]. Journal of Nanjing University of Technology, 2004, 26(2): 62-66.

[6] 孙世梅, 张红. 热管换热器传热性能及温度场数值模拟[J]. 化工学报, 2004, 55(3): 472-475.

SUN Shimei, ZHANG Hong. Numerical simulation of thermal performance and temperature field in heat pipe heat exchanger[J]. Journal of Chemical Industry and Engineering, 2004, 55(3): 472-475.

[7] 陈洁, 曹家枞. 空调排风能量回收用热管换热器的优化设计[J]. 制冷与空调, 2007, 21(3): 44-47.

CHEN Jie, CAO Jiazong. Optimum design for heat pipe heat exchanger in air-conditioning ventilation system[J]. Refrigeration and Air-Conditioning, 2007, 21(3): 44-47.

[8] 许欣. 夹套式热管传热特性试验研究及其换热器壳程压力场数值模拟[D]. 长沙: 中南大学能源科学与工程学院, 2009: 1-55.

XU Xin. Study on heat transfer characteristics of the jacketed heat pipe and numerical simulation on flow field of the exchanger[D]. Changsha: Central South University. School of Energy Science and Engineering, 2009: 1-55.

[9] 周萍, 周乃君, 蒋爱华, 等. 传递过程原理及其数值仿真[M]. 长沙: 中南大学出版社, 2006: 299-301.

ZHOU Ping, ZHOU Naijun, JIANG Aihua, et al. Principle and numerical stimulation of transport process[M]. Changsha: Central South University Press, 2006: 299-301.

[10] Zhang C, Sousa A C M, Venart J E S. The numerical and experimental study of a power plant condenser[J]. Heat Transfer, 1993, 115(2): 435-445.

[11] Jacobi A M, Shall R K. Heat transfer surface enhancement through the use of longitudinal vortices: A review of recent progress[J]. Experimental Thermal and Fluid Science, 1995, 11(3): 295-309.

[12] 张岭. 夹套式热管换热器多场数值模拟与优化研究[D]. 长沙: 中南大学能源科学与工程学院, 2010: 1-72.

ZHANG Ling. Numerical simulation and optimum research on jacket-type heat pipe heat exchanger[D]. Changsha: Central South University. School of Energy Science and Engineering, 2010: 1-72.

[13] 邓斌, 陶文铨, 余汪洋. 来流不均匀性对冷凝器性能影响的数值模拟研究[J]. 制冷与空调, 2007, 21(3): 1-6

DENG Bin, TAO Wenquan, YU Wangyang. Numerical investigation of condensers with non-uniform air distribution[J]. Refrigeration and Air-Conditioning, 2007, 21(3): 1-6.

[14] 史美中, 王中铮. 热交换器原理与设计[M]. 南京: 东南大学出版社, 2005: 275-278.

SHI Meizhong, WANG Zhongzheng. Principia and design of heat transfer device[M]. Nanjing: Southeast University Press, 2005: 275-278.

[15] 王玉琴, 宋天民, 张国福. 椭圆管管壳式换热器壳程传热性能的试验研究[J]. 压力容器, 2008, 25(10): 11-15.

WANG Yuqin, SONG Tianmin, ZHANG Guofu. Experiment research on heat transfer performance in shell of the shell-and-tube heat exchanger with elliptic tube[J]. Pressure Vessel Technology, 2008, 25(10): 11-15.

(编辑  陈灿华)

收稿日期：2012-09-10；修回日期：2012-11-23

基金项目：湖南省科技计划项目(2007CK3070)

通信作者：涂福炳(1966-)，男，湖南邵阳人，博士，副教授，从事热工过程设备仿真优化、工业节能和余热利用技术研究；电话：13908439589；E-mail: fbtu@csu.edu.cn