J. Cent. South Univ. Technol. (2009) 16: 0677-0682
DOI: 10.1007/s11771-009-0112-5

Energy consumption in rock fragmentation at intermediate strain rate
HONG Liang(洪 亮)1, 2, ZHOU Zi-long(周子龙)1, YIN Tu-bing(尹土兵)1,
LIAO Guo-yan(廖国燕)1, YE Zhou-yuan(叶洲元)1
(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. Department of Civil Engineering, Hunan City University, Yiyang 413000, China)
Abstract: In order to determine the relationship among energy consumption of rock and its fragmentation, dynamic strength and strain rate, granite, sandstone and limestone specimens were chosen and tested on large-diameter split Hopkinson pressure bar (SHPB) equipment with half-sine waveform loading at the strain rates ranging from 40 to 150 s-1. With recorded signals, the energy consumption, strain rate and dynamic strength were analyzed. And the fragmentation behaviors of specimens were investigated. The experimental results show that the energy consumption density of rock increases linearly with the total incident energy. The energy consumption density is of an exponent relationship with the average size of rock fragments. The higher the energy consumption density, the more serious the fragmentation, and the better the gradation of fragments. The energy consumption density takes a good logarithm relationship with the dynamic strength of rock. The dynamic strength of rock increases with the increase of strain rate, indicating higher strain rate sensitivity.
Key words: rock; large-diameter SHPB test; intermediate strain rate; energy consumption density; fragment distribution; dynamic strength
1 Introduction
The dynamic fragmentation of rock is a fundamental activity that lies in the operation of many manufacturing and recovery processes, most notably during crushing in the minerals and aggregates industries, during blasting in quarries and tunnels and in the action of some rock cutting processes [1-3]. The rock fragmentation is essentially a process of energy consumption. The energy consumption analysis is the key approach to illuminate the mechanism of rock fragmentation [4].
In current percussive drilling, blasting, crushing, and grinding, the effective energy used in rock breakage is found to be quite low in comparison with the total input energy. According to Ref.[5], it was estimated that only 10% of the input energy was used to break rock in cutting and drilling, the energy used in rock fragmentation varied from 5% to 15% in blasting, and the energy utilization was of the order of 3% at the maximum in grinding. Lots of effort has been paid to the study on the relationship between rock fragmentation and energy consumption by now. Laboratory tests of rock specimens with Brazilian test (e.g. BOHLOLI and HOVEN [6]), split Hopkinson pressure bar (SHPB, e.g. LI et al [7]), drop-weight test (e.g. REDDISH et al [3], WHITTLES et al [4]) or impact load cell and ultrafast load cell (e.g. TAVARES and KING [8]) showed that the degree of fragmentation increased with the impact loading or loading rate. Some simulation procedures, such as the distinct element method (e.g. COUROYER et al [9]), PFC3D (e.g. WHITTLES et al [4]), FLAC (e.g. REDDISH et al [3]), and theory (e.g. WEICHERT [10]) showed similar conclusions. The research by LI et al [11] indicated that there was a certain relationship between the degree of fragmentation and the energy consumption density. And the higher the density, the greater the degree of rock fragmentation. All these researches have made great contribution to the development of rock fragmentation and the knowledge of rock mechanics. However, owing to the complexity of rock properties, most of the results are rather qualitative.
In this work, granite, sandstone and limestone specimens were tested on large-diameter SHPB equipment at the strain rates ranging from 40 to 150 s-1 to investigate their energy consumption characteristics.
2 Test equipment
Since Hopkinson pressure bars are successfully used to measure the dynamic properties of materials in compression, the SHPB increasingly becomes the standard method to measure the dynamic mechanical
properties of the material at high strain rates [12]. With the assumption of one dimensional stress wave theory, the specimen’s dynamic stress σs(t), strain rate  and strain εs(t) can be determined with incident strain
and strain εs(t) can be determined with incident strain  and reflected strain
and reflected strain 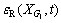 recorded by strain gauge G1 on the input bar, and transmitted strain
recorded by strain gauge G1 on the input bar, and transmitted strain 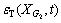 recorded by strain gauge G2 on the output bar.
recorded by strain gauge G2 on the output bar.
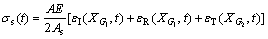 (1a)
(1a)
 (1b)
(1b)
 (1c)
(1c)
where A, E and C0 are the cross sectional area, dynamic elastic modulus and longitudinal elastic wave velocity of elastic bar, respectively; As and ls are the specimen’s cross sectional area and length, respectively; and t is the propagation time of the stress wave.
For heterogeneous brittle materials like rock and concrete, if the specimen is processed too small, it will not represent the authentic properties of specimen [1]. In SHPB test, the diameter of specimen should match the diameter of elastic bar to ensure the stress uniformity, especially the radial stress in specimen. So the large-diameter SHPB equipment must be developed. The set-up of 75 mm diameter SHPB developed by LI et al [7] was used in this study. The diameter and length of the input and output solid circular bars are 75 and 2 000 mm, respectively. Longitudinal elastic wave velocity and density of the bars are 5.400 km/s and 7.810 g/cm3, respectively.
In the conventional SHPB equipment, the striker is a solid circular bar with the same diameter and material as the input/output bars. This arrangement initiates an approximate rectangular loading pulse that has a relatively small rising slope. While many researches indicated that the rectangular stress wave would generate waveform oscillation when it propagated along the bars because of the relatively abundant wave frequency spectrum. The wave oscillation would significantly increase with the increase of the impact loading, the propagation distance and the elastic bar diameter [1, 13-14]. Due to the relatively low elastic modulus and strength of rock materials, as compared to those of metal materials, the oscillation of the incident wave, reflected wave and transmitted wave in a conventional SHPB will result in random oscillation of resultant test curves. Because of its small failure strain, the specimen of brittle rock always breaks during the initial rising slope or oscillatory part of loading waves. This makes it impossible to obtain the true rock properties. So it is impossible to obtain accurate and effective results with conventional circular striker that produces rectangular incident wave [15-16].
Producing a slope rising incident wave with few frequency components seems to be the best solution to overcome the defects of rectangular wave.
The striker whose structure was obtained by inverse design [17-18] was used in SHPB tests. It can produce a half-sine incident wave that has a relatively mild rising slope, and can also avoid the oscillation effectively.
3 Test samples and properties
The samples used in SHPB tests were cored from the same granite block, sandstone block or limestone block. The length-to-diameter ratio (L/D) of sample was controlled about 0.5 to reduce the inertial effect and end effect (The length-to-diameter ratio of the sample is  when the inertial effect is zero, where μ is the Poisson ratio [19]). All the test samples were labeled according to the cores from which the samples were prepared. For example, test sample “2-1” indicates the first sample obtained from the second core. The dimensions, mass and P-wave velocity of samples were measured after air-dry (see Table 1).
when the inertial effect is zero, where μ is the Poisson ratio [19]). All the test samples were labeled according to the cores from which the samples were prepared. For example, test sample “2-1” indicates the first sample obtained from the second core. The dimensions, mass and P-wave velocity of samples were measured after air-dry (see Table 1).
Table 1 Characteristics of samples

To obtain the static strength and deformation properties of granite, sandstone and limestone, cored samples with L/D=2 were tested on an electro-hydraulic servo control material testing machine of Instron 1342. The average stress—strain relationship is shown in Fig.1. It can be observed that the granite has an average static strength of 112 MPa, elastic modulus of 21.5 GPa. The sandstone has an average static strength of 85 MPa, elastic modulus of 14.5 GPa. The limestone has an average static strength of 137 MPa, elastic modulus of 26.3 GPa.
4 Experiment and result analysis
The SHPB tests were carried out in five groups for granite, sandstone and limestone, respectively. Different loading levels were employed for different groups. Specific loading level was fulfilled by changing the impact velocity of striker controlled by the position of
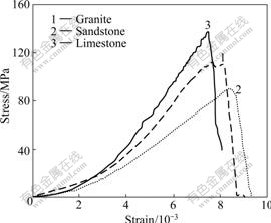
Fig.1 Average stress—strain curves of rocks (Loading rate is 0.007 5 mm/s)
striker in gas tube, or the air pressure in gas tank.
4.1 Relationship between energy consumption density and incident energy
In the SHPB test the energy consumption for rock fragmentation and its density can be determined using Eqns.2(a) and (b), respectively [2]:
WC=WI-(WR+WT) (2a)
 (2b)
(2b)
where WC is the energy consumption for rock fragmentation, WI, WR and WT donate the energy with the incident wave, reflected wave and transmitted wave, respectively, ed is the energy consumption density, and V is the specimen volume. WI, WR and WT can be determined using Eqn.(2c) [2]:
 (2c)
(2c)
where σ(t) is the stress pulse in the elastic bars at certain time of t. ρece is the impedance of the elastic bars, and Ae is the area of cross section of elastic bars.
With Eqn.(2), the incident energy, reflected energy, transmitted energy, and the energy consumption density of specimens can be calculated.
Fig.2 shows the results of the total incident energy and the corresponding energy consumption density of rocks in SHPB tests. It may be observed from Fig.2 that the energy consumption densities of granite, sandstone and limestone increase with the increase of the total incident energy. There is a good linear relationship between them. After data fitting, it is found that the relationship between the energy consumption density of rock and the total incident energy can be expressed as
ed=aWI-b (3)

Fig.2 Relationship between energy consumption density and total incident energy
where a and b are the parameters related to loading modes and lithology. In these tests the values of a, b and the correlation coefficient R are listed in Table 2. According to Eqn.(3), if ed=0, then WI=b/a≠0. This implies that there is a critical value of energy level for rock damage, i.e. when the input energy is less than the critical value, the rock will never be damaged, and the incident energy will dissipate in the form of elastic wave and noise.
Table 2 Values of a, b and correlation coefficient R

4.2 Influence of energy consumption density on fragment distribution
After tests, the broken pieces of specimens were collected and sieved. The sieve sizes were chosen to be 40.00, 20.00, 10.00, 5.00, 2.00 and 1.00 mm, respectively. After sieving, the mass fractions of fragments within a certain size span or the cumulative mass fraction of fragments passing a certain sieve size were determined by weighting.
The fragment distribution curves of granite specimens under different loading levels are given in Fig.3. In order to reflect the fragment size distribution preferably, the half-logarithm coordinate system was used for the relatively large range of fragment size. It can be seen from Fig.3 that the higher the energy consumption density, the flatter the fragment distribution curve. This indicates that the higher the energy consumption density, the more serious the fragmentation, and the better the gradation of fragment.
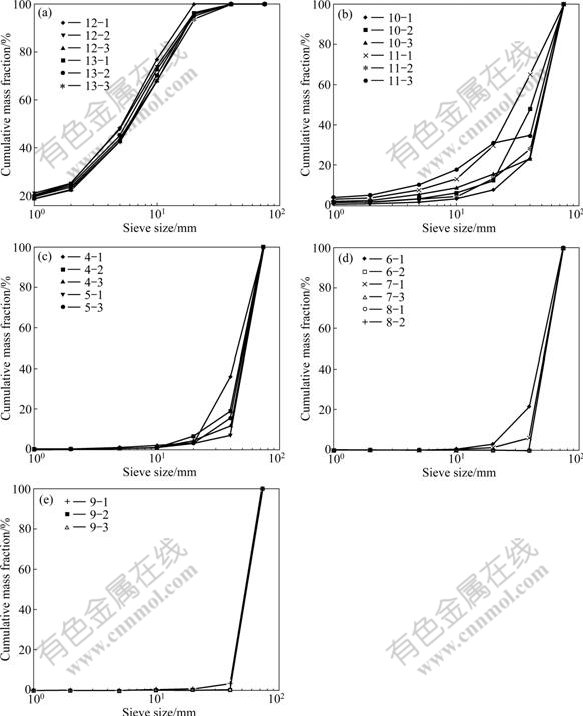
Fig.3 Cumulative frequency size distribution curves at different loading levels: (a) The 1st loading set (ed=5.423 5-5.844 3 J/cm3); (b) The 2nd loading set (ed=1.686 0-2.358 7 J/cm3); (c) The 3rd loading set (ed=0.843 1-1.075 2 J/cm3); (d) The 4th loading set (ed=0.484 5-0.703 2 J/cm3); (e) The 5th loading set (ed=0.427 0-0.468 0 J/cm3)
To quantitatively describe the fragmentation of specimens, the average fragment size of specimen is defined as
 (4)
(4)
where 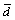 is the average fragment size of specimen after the impact test, di is the mean grain size of the fragments situated between sieves with successive mesh sizes, and ηi is the mass fraction of fragments corresponding to the size of di. According to the sieve size span in this work, d1 can be determined as (75+40)/2=57.5 mm. And d2=30 mm, d3=15 mm, d4=7.5 mm, d5= 3.5 mm, d6=1.5 mm and d7=0.5 mm can be decided accordingly.
is the average fragment size of specimen after the impact test, di is the mean grain size of the fragments situated between sieves with successive mesh sizes, and ηi is the mass fraction of fragments corresponding to the size of di. According to the sieve size span in this work, d1 can be determined as (75+40)/2=57.5 mm. And d2=30 mm, d3=15 mm, d4=7.5 mm, d5= 3.5 mm, d6=1.5 mm and d7=0.5 mm can be decided accordingly.
Fig.4 shows the calculated results of the average fragment size of granite, sandstone and limestone specimens and the corresponding energy consumption density in SHPB tests. It can be observed from Fig.4 that the average fragment size of rock specimens decreases with the increase of the energy consumption density and there is a good exponent relationship between them, which can be expressed as
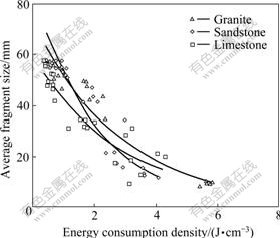
Fig.4 Relationship between average fragment size and energy consumption density of rock specimens
 (5)
(5)
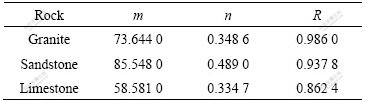
where m and n are the parameters related to loading modes and lithology. In these tests,the values of m, n and the correlation coefficient R are listed in Table 3.
Table 3 Values of m, n and correlation coefficient R
4.3 Relationship among dynamic strength, strain rate and energy consumption density
In order to describe the dynamic strength of rock, lots of studies have been carried out and some predicting formulae have been proposed. Among them, the strain rate dependence relationship has been accepted world-widely, as shown in Eqn.(6) [2]:
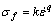 (6)
(6)
where σf is the dynamic strength of rock,  is the strain rate, k and q are the parameters related to loading modes and lithology.
is the strain rate, k and q are the parameters related to loading modes and lithology.
From test results, the dynamic strength of granite, sandstone and limestone specimens under different strain rates are obtained and shown in Fig.5. With Eqn.(6), the values of k, q and the correlation coefficient R are listed in Table 4. The R values for granite, sandstone and limestone are 0.791 8, 0.685 1 and 0.673 3, respectively, which indicates that Eqn.(6) describes the strain rate dependence of rock dynamic strength to some extent, but the large discrepancy still exists at the intermediate strain rates.

Fig.5 Relationship between dynamic strength of rock and strain rate
Table 4 Values of k, q and correlation coefficient R

According to the thermodynamics law, the failure process of material is essentially a procedure of energy absorption, transformation and release. Therefore, the strength characteristics of material under the external loading should be better interpreted with the concept of energy consumption. Usually, the energy consumption of material is evaluated with the energy consumption density. So the dynamic strength of material should be described with energy consumption density.
Fig.6 gives the scatter diagram between dynamic strength and energy consumption density for specimens of granite, sandstone and limestone. The fitting curves indicate that there is a good logarithm relationship between the rock dynamic strength and its energy

Fig.6 Relationship between dynamic strength and energy consumption density
consumption density with the expression as follows:
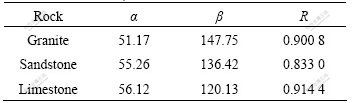
σf=αln ed+β (7)
where α and β are the parameters related to loading modes and lithology.
The fitting values of α, β and the correlation coefficient R for the three kinds of rock are listed in Table 5. It can be seen that their R values are 0.900 8, 0.833 0 and 0.914 4, respectively, indicating the good prediction ability of Eqn.(7), and the dynamic strength of rock can be perfectly predicted with the energy consumption density of specimen.
Table 5 Values of α, β and correlation coefficient R
5 Conclusions
(1) The energy consumption density increases in a good linear relationship with the total incident energy.
(2) The higher the energy consumption density, the more serious the fragmentation, and the better the gradation of fragment. The energy consumption density is of an exponent relationship with the average size of rock fragments.
(3) The dynamic strength of rock depends on and increases with the increase of the strain rate. The strain rate sensitivity varies with the lithology.
(4) The dynamic strength of rock takes a good logarithm relationship with the energy consumption density, which can be perfectly predicted with the energy consumption density of specimen.
References
[1] LI X B, LOK T S, ZHAO J, ZHAO P J. Oscillation elimination in the Hopkinson bar apparatus and resultant complete dynamic stress—strain curves for rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(7): 1055-1060.
[2] LI Xi-bing, GU De-sheng. Rock impact dynamics [M]. Changsha: Central South University of Technology Press, 1994. (in Chinese)
[3] REDDISH D J, STACE L R, VANICHKOBCHINDA P, WHITTLES D N. Numerical simulation of the dynamic impact breakage testing of rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(2): 167-176.
[4] WHITTLES D N, KINGMAN S, LOWNDES I, JACKSON K. Laboratory and numerical investigation into the characteristics of rock fragmentation [J]. Minerals Engineering, 2006, 19(14): 1418-1429.
[5] ZHANG Z X, KOU S Q, JIANG L G, LINDQVIST P A. Effects of loading rate on rock fracture: fracture characteristics and energy partitioning [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 745-762.
[6] BOHLOLI B, HOVEN E. A laboratory and full-scale study on the fragmentation behavior of rock [J]. Engineering Geology, 2007, 89(1): 1-8.
[7] LI X B, LOK T S, ZHAO J. Dynamic characteristics of granite subjected to intermediate loading rate [J]. Rock Mechanics and Rock Engineering, 2005, 38(1): 21-39.
[8] TAVARES L M, KING R P. Single-particle fracture under impact loading [J]. International Journal of Mineral Processing, 1998, 54(1): 1-28.
[9] COUROYER C, NING Z, GHADIRI M. Distinct element analysis of bulk crushing: Effect of particle properties and loading rate [J]. Powder Technology, 2000, 109(1): 241-254.
[10] WEICHERT R. Theoretical prediction of energy consumption and particle size distribution in grinding and drilling of brittle materials [J]. Particle and Particle Systems Characterization, 1991, 8(1): 55- 62.
[11] LI Xi-bing, LAI Hai-hui, GU De-sheng. Energy absorption of rock fragmentation under impulsive loads with different wave forms [J]. Transactions of Nonferrous Metals Society of China, 1992, 2(4): 10-14. (in Chinese)
[12] FIELD J E, WALLEY S M, PROUD W G, GOLDREIN H T, SIVIOUR C R. Review of experimental techniques for high rate deformation and shock studies [J]. International Journal of Impact Engineering, 2004, 30(7): 725-775.
[13] LI Xi-bing, HONG Liang, YIN Tu-bing, ZHOU Zi-long, YE Zhou-yuan. Relationship between diameter of split Hopkinson pressure bar and minimum loading rate under rock failure [J]. Journal of Central South University of Technology, 2008, 15(2): 218-223.
[14] ZHAO H, GERARD G, KLEPACZKO J R. On the use of viscoelastic split Hopkinson pressure bar [J]. International Journal of Impact Engineering, 1997, 19(4): 319-330.
[15] LI Xi-bing, GU De-sheng, LAI Hai-hui. On the reasonable loading stress waveforms determined by dynamic stress-strain curves of rocks by SHPB [J]. Chinese Journal of Explosion and Shock Waves, 1993, 13(2): 125-130. (in Chinese)
[16] LOK T S, LI X B, LIU D, ZHAO P J. Testing and response of large diameter brittle materials subjected to high strain rate [J]. Journal of Materials in Civil Engineering, 2001, 14(3): 262-269.
[17] LIU De-shun, LI Xi-bing. Dynamic inverse design and experimental study of impact piston [J]. Chinese Journal of Mechanical Engineering, 1998, 34(4): 506-514. (in Chinese)
[18] LI Xi-bing, ZHOU Zi-long, WANG Wei-hua. Construction of ideal striker for SHPB device based on FEM and neural network [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(23): 4215-4218. (in Chinese)
[19] DAVIES E D H, HUNTER S C. The dynamic compression testing of solids by the method of the split Hopkinson pressure bar [J]. Journal of the Mechanics and Physics of Solids, 1963, 11(3): 155-179.
(Edited by CHEN Wei-ping)
Foundation item: Projects(50674107, 10472134, 50490274) supported by the National Natural Science Foundation of China
Received date: 2008-10-12; Accepted date: 2009-01-06
Corresponding author: HONG Liang, PhD; Tel: +86-13974801644; E-mail: hongliangcus@163.com