基于二次退火机制的改进多态蚁群算法

杜振鑫^1,2，王兆青²，王枝楠²，秦伟²，段云涛²

(1. 韩山师范学院 基础教育师资系，广东 潮州，521041；

2. 浙江理工大学 计算机技术教研部，浙江 杭州，310018)

摘要：利用多态蚁群算法和模拟退火算法的优点提出一种新的融合优化算法。研究结果表明：模拟退火用于优化每轮迭代后的路径，使得信息素释放更好的反映路径的质量；退火思想同时用于信息素更新机制，避免算法早熟、停滞，较差的路径按照退火竞争机制释放信息素；由于每轮迭代最优路径释放信息素最多，对其进行3-opt优化，提高搜索效率。同时，新发现的最优路径允许释放更多的信息素，使得蚂蚁在后续迭代中能够记住这条新路径。实验结果验证了算法的有效性。

关键词：多态蚁群算法；模拟退火；信息素；3-opt

中图分类号：TP18          文献标志码：A         文章编号：1672-7207(2011)10-3112-06

Improved polymorphic ant colony algorithm with

double simulated annealing

DU Zhen-xin^1,2, WANG Zhao-qing², WANG Zhi-nan², QIN Wei², DUAN Yun-tao²

(1. Department of Basic Education Teachers, Hanshan Normal University, Chaozhou 521041, China;

2. Instructional Division of Computer Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Abstract: Using each advantage of polymorphic ant colony algorithm (PACA) and simulated annealing (SA), a new hybrid algorithm was proposed. The results show that SA is applied to shorten the length of each path after every round of search,so that the increment of pheromone can effectively reflect the quality of a path. The idea of SA is also applied to the pheromone release mechanism to avert precocity and stagnation, thus the inferior paths can release the pheromone by the competition mechanism based on SA. The 3-opt strategy is applied to the best path of every round of search to improve the search efficiency because it plays the most important role in releasing pheromone. Meanwhile, the newly discovered path is better and can release more pheromone so that the ants can “remember” the new path in the follow-up iterations. Experiment results show the effectiveness of the proposed algorithm.

Key words: polymorphic ant colony algorithm; simulated annealing; pheromone; 3-opt

TSP(Traveling salesman problem)问题是典型的NP(Non-deterministic polynomial problem)难问题^[1]，在车辆调度、工程控制、VLSI设计等领域具有重要用途^[2]，目前不存在多项式复杂度以内的全局算法^[3]，可以将其简述为：求1条经过n个城市1次且仅1次的闭合回路，使其最短。Dorigo等^[4]提出的蚁群算法是目前求解TSP问题最有效的算法之一^[5]。观察已知的TSP最短路径可以发现其应当满足3个基本原则：(1) 空间距离最近的城市应当在TSP最短路径中尽可能相邻；(2) 距离最远的2个城市中间应尽可能插入其他城市；(3) 最优路径中绝无子路径交叉现象。徐精明等^[6]提出的多态蚁群算法在蚂蚁选路时只从最近的n_MAXPC个城市中选择，在很大程度上减少了计算量，较好地满足了第1个原则，本文作者在此基础上加以改进，使之同时满足3个原则。同时，本文作者提出基于竞争机制更新信息素、新路径信息素加强和压缩信息素的机制，使得算法不容易陷入局部最优解。

1  多态蚁群算法

基本蚁群算法有2个主要步骤，即蚂蚁构建问题的解和信息素更新。τ_ij表示t时刻城市i和j之间的信息素浓度，第k(k=1，2，…，m)只蚂蚁在搜索过程中根据路径上遗留的信息素浓度决定下一步访问的城市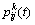，表示t时刻蚂蚁k由城市i访问城市j的概率：

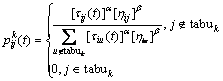
式中：η为启发信息，一般取η=1/d_ij；d_ij为路径ij的长度；α和β分别表示信息素和启发信息的重要程度。tabu_k表示蚂蚁k已经访问过的城市。

所有蚂蚁完成1次循环以后，各路径上的信息素更新：

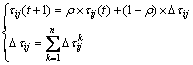
其中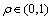：为挥发系数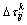；表示第k只蚂蚁本次循环中留在路径ij上的信息素浓度：

其中：Q为设定的常数。

基本蚁群算法中的蚂蚁只有1种，不能完全反映真实蚂蚁群体的复杂性，而且蚂蚁由当前城市i访问下一个城市时要从剩下的所有城市中选择1个，搜索空间过大，而实际最优路径只可能经过城市i最近的n_MAXPC个城市之一^[7]。据此，徐精明等^[6]提出了多态蚁群算法(Polymorphic ant colony algorithm，PACA)，主要的改进是将蚂蚁分为侦察蚁和搜索蚁。首先将m个侦察蚁分别放置在m个城市中，每个侦察蚁以所在城市为中心，侦查其余m-1个城市，将结果与先验知识相结合记为s[i][j]，标记在路径ij上：

其中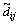：表示以城市i为中心到其余m-1个城市的最短距离。据此结果，首先置初始时刻各条路径上的信息量如下：

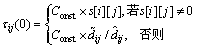
式中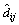：表示以i为中心到其他m-1个城市的最大距离；C_onst为常量。搜索蚁负责全局搜索，第k个搜索蚁在t时刻由城市i访问城市j的概率为：

2  多态蚁群算法的缺陷及改正

多态蚁群算法中搜索蚁只从最近的n_MAXPC个城市中选择城市，减轻了选路计算量。但是，若最近的n_MAXPC个城市全部访问完时(如图1所示)，假设n_MAXPC为3，则当蚂蚁从1号城市走到4号城市时，因为4号城市邻近的n_MAXPC=3个城市全部选择完毕，蚂蚁无路可走。实际上，出现图中所示情况的概率很小，但是，为了使算法不失严谨性，仍然应当从理论上予以避免。采用增大n_MAXPC的办法可以避免上述情况。实验发现：对于100个城市TSP问题，至少应当满足：

取40个城市以上才能完全避免上述问题，但是，这又丧失了多态蚁群算法减少选路计算量的优点，而且算法运行中一般只有少数几只蚂蚁出现无法选路的情况。本文在不增大n_MAXPC的情况下将概率选择公式改为式(7)。根据式(7)，蚂蚁选路时仍然主要从邻近的n_MAXPC个城市中选路，只有无法选路时才会采用上式中s[i][j]=0的情况，兼顾了多态蚁群算法快速收敛的优点，又使得算法不至于停滞。

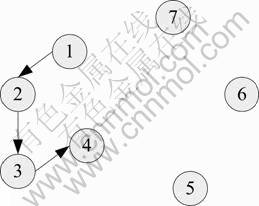
图1  多态蚁群算法停滞示意图

Fig.1  Phenomenon of PACA’s falling into stagnation

3  基于二次退火机制的改进多态蚁群算法

本文改进的主要思想是通过退火和局部优化使得多态蚁群算法满足TSP最短路径三原则。为了避免算法局部收敛，对信息素更新方式加以改进，采用模拟退火竞争释放机制，使得信息素更新多样化。同时，对新发现最优路径信息素加强和信息素压缩，减少信息素浓度差。

张晓婧等^[8]也提出了基于模拟退火的蚁群算法，但是容易导致早熟收敛，并且退火时仅使用普通的随机交换城市的方案，效率不够高。刘波等^[9]提出模拟退火和回火策略的蚁群算法，可以有效缓解基本蚁群算法容易早熟、停滞和收敛较慢的问题，但是，蚂蚁每次选路在所有路径中随机选择，其效率仍然有待于进一步提高。

3.1  一次退火优化路径

根据引言中提出的原则(2)，距离越远的2个城市中间应当以越大的概率插入其他城市，使路径总长度尽可能地减小。退火过程可分4步完成。

(1) 在当前蚂蚁形成的TSP路径中，以较大的概率选择2个距离较远的相邻城市，其中起点城市记为i，则终点城市为i+1。假设当前蚂蚁找到的TSP路径是C₀，以数组l(k)表示路径C₀中相邻2个城市之间的距离，那么有：

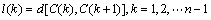
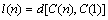
其中：d表示距离。则选取起点城市i的概率为：

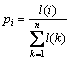
根据式(9)，空间距离越远的2个城市越容易被选中，从而在这2个城市中间插入其他城市使得路径缩短的概率也越大。

(2) 由第一步选择的城市i，进一步选择插入i和i+1之间的城市。根据引言中提出的思想，应当让距离越近的城市以越大的概率相邻。设d_max表示距离城市i最远的城市的距离，即d_max=max(k(i，j))，j为i的相邻城市，为了防止下一步选择的城市是当前城市本身，设置d(i，i)=d_max，则选取插入i和i+1之间的城市j的概率为：

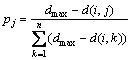
假设根据式选出的在TSP路径中相邻、而空间距离较远的城市是i和i+1，在式中选出的“距离起点城市i较近的”的城市是j，则j被插入在i和i+1之间，形成子路径i，j和i+1，使得引言部分提出的前2条原则同时得到满足。

(3) 假设经上述2步以后C₀变为C₁，则以模拟退火原则决定保留C₁还是C₀：计算路径长度L(C₁)和L(C₀)的差值?L=L(C₁)-L(C₀)，若?L＜0，则用C₁替换C₀；否则若exp(-?L/T)＞rand(0，1)，则也用C₁替换C₀，否则，就保留C₀而抛弃C₁。退火温度按照T(t+1)=λT(t)进行迭代(λ为退火系数)。此处的退火温度T和下面的二次退火温度为同一个温度。

(4) 每条路径C_i在第t次迭代时的退火温度恒定不变，都为T(t)。每条路径的退火次数：首先对各条路径长度按照从小到大排序，形成排序队列q_i(1≤i≤m，m为蚂蚁的个数)，第i条路径的退火次数为，因为较好的路径释放信息素的可能性较大，所以，退火次数较多；较差路径释放信息素的可能性较小，所以，退火次数较少，使得信息素释放更好地反映路径的质量。

3.2  最优路径3-opt修正

3-opt修正的原理可以用图2表示。图2中，实线(包含粗实线和细实线)所示是修正前的路径，城市j是距离城市i最近的城市，那么将图中3条粗实线3条路段用3条虚线路段代替，路径变短的可能性很大，交叉，因为若该路径含有交叉，则必定不是最优路径，必然可以被3-opt优化；反之，经过3-opt优化的路径，必定不含交叉。

从而原来实线所示路径以较大概率得到优化。通过3-opt优化，基本可以满足引言中的原则(3)：最优路径不含

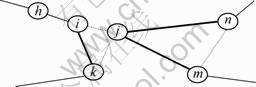
图2  3-opt修正原理

Fig.2  Principle of 3-opt

3.3  二次退火竞争释放信息素

信息素是蚁群算法中最重要的启发因素，因此，其释放方式十分重要。主要的信息素释放方式有2种：

一是全局释放信息素方式。其特点是所有蚂蚁都贡献信息素，优点是不容易陷入局部最优解，缺点是收敛速度较慢；

二是精英蚂蚁系统。其特点是只有当次迭代最优的蚂蚁才有释放信息素的权利，优点是只有较优路径才能释放信息素，所以算法收敛速度较快，缺点是容易使算法陷入局部最优解，对初始信息素分布敏感。

Dorigo等^[10-11]提出限制路径上的信息素浓度，减少优势路径的选择压力；Zhu等^[12]提出信息素变异和动态更新的机制，这些改进方案的目的都是为了一方面避免优势路径上的信息素过度积累，增强算法跳出局部最优解的能力，另一方面又要保证算法快速收敛，取得全局和局部寻优之间的平衡。本文结合现有信息素释放方式的优点，提出一种退火竞争释放信息素的方式。

(1) 变量定义：假设搜索蚁的数目是m，以A_k(C_k，L_k)表示第k(k=1，2，…，m)只搜索蚁搜索到的路径，C_k是该只蚂蚁生成的TSP路径，L_k是该路径的长度。{A_k(C_k，L_k)|1≤k≤m}表示m只蚂蚁形成的路径集合。A_tmin(C_tmin，L_tmin)是第t次迭代生成的最优路径，即满足L_tmin=min(L_k)，第k只(k=1，2，…，m)的蚂蚁，C_tmin是其经过的TSP路径，L_tmin是其TSP路径的长度。 A_min(C_min，L_min)表示直到第t次迭代时算法找到的最短路径，C_min表示其TSP路径，L_min表示其路径长度。T(t)表示模拟退火的第t次迭代温度，初始温度为T₀。

(2) 各蚂蚁竞争获得释放信息素的权利：采用竞争释放信息素的机制，计算当次迭代中候选集{A_k(C_k，L_k)+1≤k≤m}中的每一个路径L_k，计算

?L=L_k-L_tmin

p_k=exp(-?L/T(t))，如果?L＞0      

若?L=0，则该只蚂蚁k释放信息素的竞争标记f_k=1；若p＞rand(0，1)，则竞争标记f_k=1。否则f_k=0。

(3) 竞争成功者释放信息素：

其中：ρ为信息素挥发系数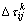；为每轮迭代结束后竞争成功的蚂蚁在路径(i，j)上释放的信息素；ω为固定常数，作用是对当前为止最优路径A_min(C_min，L_min)上的信息素加强ω倍，使得上式兼顾了全局和局部2个原则。

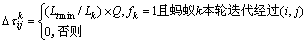
式中：Q为信息素释放常数；Δτ_min是直到第t次迭代为止，算法找到的全局最优路径在路段(i，j)上释放的信息素：

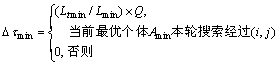
(4) 回火机制。当每轮搜索完成，蚂蚁释放信息素以后，对退火控制参数T(t)降温：

T(t+1)=λT(t)                  

其中：λ为退火系数，决定了退火温度T下降的速度。退火温度T决定了上一步释放信息素过程中竞争成功的蚂蚁的个数，若T取值较大，则上一步计算的竞争概率p_k就较大，蚂蚁竞争成功的个数就比较多，有利于信息素均匀分布，使得算法侧重于全局搜索，避免过早陷入局部最优解；随着退火温度T的逐步下降，竞争概率减小，竞争成功的蚂蚁越来越少，最后，只有接近本次迭代最优解A_tmin(C_tmin，L_tmin)的蚂蚁才能获得释放信息素的权利，促进算法加速收敛。本算法使用较小的退火系数λ促使算法快速收敛，但是，这有可能引起算法陷入局部最优。所以，采用多次回火机制，当温度T从T₀下降到T_min时，将温度T重新回火为T_max(T_max＜T₀)，重新开始退火。本文称这种机制为回火机制。实验中发现只要退火系数λ和最大回火次数N_Smax控制得当，能够取得比单一退火机制更快的收敛速度，且算法更容易跳出局部最优解。

3.4  新路径信息素加强和信息素压缩

蚁群算法在迭代中偶尔发现更优的路径，由于信息素浓度得不到及时增大，会因为挥发机制很快被遗忘，使得算法探测功能逐渐减弱。因此，提出对新路径上不属于老路径的路段的信息素加强方法：

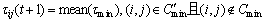
式中：C′_min表示新的全局最优路径；C_min表示老的全局最优路径；mean(τ_min)为C_min路径上所有路段(i，j)的信息素浓度平均值。

蚁群算法容易局部收敛的另一个原因是迭代后期路径上的信息素浓度相差过大，使得蚂蚁搜索空间越来越小，最后陷入局部最优解。特别对于大规模TSP问题，由于算法迭代次数较多，使得路径上的信息素浓度相差更大，很容易使算法陷入局部最优解。为了解决这个问题，Stutzle等^[11]提出了最大-最小蚂蚁系统，通过在算法中设置信息素浓度上限τ_max和下限τ_min，抑制信息素浓度相差过大的情况，算法性能有了较大改进。但是，如果τ_max设置过大或者τ_min设置过小，仍然会导致信息素浓度相差过大；如果τ_max设置过小或者τ_min设置过大，会使得优势路径上的信息素浓度都等于τ_max，较差路径上的信息素浓度都等于τ_min，从而失去了信息素的区分作用，算法趋近于随机算法，不利于算法收敛，所以，很难准确地设置τ_max和τ_min。为了弥补这一缺陷，付治政等^[13]提出一种压缩信息素浓度的方法，但其算法需要对信息素浓度分段考虑，并且采用的分段参数不容易控制，且不能保证压缩后信息素的顺序。本文提出一种信息素压缩方法，既能保持信息素浓度的小顺序，又能避免浓度相差过大。算法中只设置一个信息素浓度下限τ_min，不设置信息素浓度上限τ_max。当路径上的最大信息素浓度max(τ)和最小信息素浓度min(τ)的比值大于固定值R时，所有路径上的信息素执行以下压缩操作：

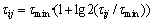
经过压缩以后，各路径上的信息素浓度顺序仍保持不变，但是比值被大幅度减小，有利于为下一次迭代提供均等的机会。

3.5  算法流程

以上描述的基于二次退火机制的改进多态蚁群算法(Double simulated annealing based PACA，DSAPACA)算法具体步骤如下。

Step 1：初始化各参数，按式初始化各路径信息素；

Step 2：迭代计数器N_C=0。

Step 3：将m只搜索蚁随机放入n个城市中，并将该城市放入每只搜索蚁的禁忌表tabu中；

Step 4：按照改正的概率转移式选择每只蚂蚁下一步前进的城市，并将该城市放入每只蚂蚁的禁忌表中，直到所有蚂蚁都完成1次遍历，生成候选路径集合{A_k(C_k，L_k)|1≤k≤m}。

Step 5：对于{A_k(C_k，L_k)|1≤k≤m}集合中的每一条路径，按式和(10)进行1次退火过程，生成新的候选解集合{A′_k(C′_k，L′_k)|1≤k≤m}，并在该集合中确定本轮迭代最优解A_tmin(C_tmin，L_tmin)。

Step 6：对A_tmin(C_tmin，L_tmin)按照3-opt原理进行修正，生成新的迭代最优解A′_tmin(C′_tmin，L′_tmin)。若其优于全局最优解A_min(C_min，L_min)，则A_min(C_min，L_min)= A′_tmin(C′_{t min}，L′_{t min})。

Step 7：对{A′_k(C′_k，L′_k)|1≤k≤m}中的每个路径按照式和竞争释放信息素；按照式更新退火温度；若退火温度T(t)＜T_min，则进行回火，即T(t)=T_min，同时，回火次数N_S=N_S+1；若N_S＞N_Smax，则输出最优解并退出循环，否则继续进行下一步。

Step 8：对各条路径上的信息素按照式对新的全局最优路径上的信息素加强，按照式信息素进行压缩。

Step 9：Δτ_ij重新初始化为0，tabu表重新置空，迭代计数器N_C=N_C+1。若达到循环结束条件，则转Step 10；否则，转Step 3。

Step 10：输出全局最优解并退出循环。

4  实验与分析

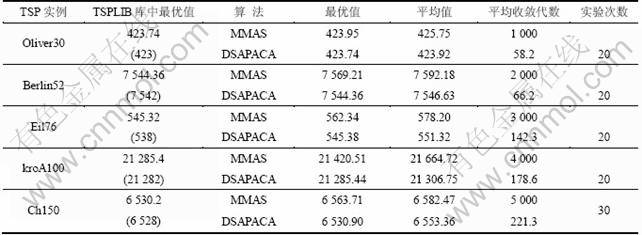
DSAPACA算法参数设置为：α=1，β=3，m=城市规模，ρ=0.15，Q=20，τ_min=0.5，R=30，ω=2。对于城市规模小于100的TSP问题，M_AXPC =10，退火参数设置为：初始温度T₀=10⁵，退火系数λ=0.95，[T_max，T_min]=[10⁴，30]，最大回火次数N_Smax=4。对于城市规模大于等于100的TSP问题，M_AXPC=15，退火参数设置为：T₀=10⁶，退火系数λ=0.96，[T_max，T_min]=[10⁵，30]，最大回火次数N_Smax=6。MAX-MIN算法的参数设置参照文献[13]。表1所示为2种算法对5个TSP问题的测试结果。从表2可以看出：DSAPACA算法在5个不同规模的TSP问题中收敛精度和速度都比MMAS算法的高，且问题规模越大其优势越明显，DSAPACA的最优值也与TSPLIB库中的最优值非常接近。

表1  TSP问题测试结果

Table 1  Search results of  TSP

5  结论

(1) 改正了基本多态蚁群存在的选路方面的缺陷，在此基础上加以改进，使其满足最短路径三原则。

(2) 通过一次退火，以较大概率使得“空间距离越近的城市在TSP路径中以越大的概率相邻”，并且改进算法充分利用原有多态蚁群算法中的“侦查素”,无需额外计算。通过二次退火，使得信息素释放大体围绕最优路径呈正态分布，既保证了优势路径释放较多的信息素，又增加了较差路径的释放机会，避免信息素单一释放机制引起的局部最优现象。

(3) 改进算法收敛速度较快，精度较高。

参考文献：

[1] Garey M R, Johnson D S. Computer and intractability: A guide to the theory of NP-completeness[M]. New York: Freeman, 1979: 18-19.

[2] Michalewicz Z, Fogel D B. How to solve it: Modern heuristick[M]. Berlin Heidelberg: Spring-Verlag, 2000: 37-38.

[3] Salman A, Ahmad I, Al-Madani S. Particle swarm optimization for task assignment problem[J]. Microprocessors and Microsystems, 2002, 26: 363-371.

[4] Dorigo M, Socha K. An introduction to ant colony optimization[R]. Belgium: Universite Libre de Bruxelles, 2006: 7-9.

[5] 段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社, 2006: 45-96.
DUAN Hai-bin. Ant colony algorithms: Theory and applications[M]. Beijing: Science Press, 2006: 45-96.

[6] 徐精明, 曹先彬, 王煦法. 多态蚁群算法[J]. 中国科学技术大学学报, 2005, 35(1): 59-65.
XU Jing-ming, CAO Xian-bin, WANG Xu-fa. Polymorphic ant colony algorithm[J]. Journal oF University of Science and Technology of China, 2005, 35(1): 59-654.

[7] 全惠云, 文高进. 求解TSP子空间的遗传算法[J]. 数学理论与应用, 2002, 22(1): 36-39.
QUAN Hui-yun, WEN Gao-jin. Subspace genetic algorithm for TSP[J]. Mathematical Theory and Applications, 2002, 22(1): 36-39.

[8] 张晓婧, 高慧敏. 基于模拟退火的蚁群算法求解Job-Shop问题[J]. 计算机应用与软件, 2008, 25(5): 77-79.
ZHANG Xiao-jing, GAO Hui-min. Application of ant colony optimization based on simulated annealing to job-shop problem.[J]. Computer Applications and Software, 2008, 25(5): 77-79.

[9] 刘波, 蒙培生. 采用基于模拟退火的蚁群算法求解旅行商问题[J]. 华中科技大学学报: 自然科学版, 2009, 37(11): 26-30.
LIU Bo, MENG Pei-sheng. Simulated annealing-based ant colony algorithm for traveling salesman problems[J]. Huazhong University of Science and Technology: Natural Science Edition, 2009, 37(11): 26-30.

[10] Dorigo M, Stutzle T. Ant colony optimization[M]. London: MIT Press, 2004: 153-172.

[11] St Stutzle T, Hoos H. Max-Min ant system[J]. Future Generation Computer System, 2000, 16(9): 889-914.

[12] Zhu Q B, Yang Z J. An ant colony optimization algorithm based on mutation and dynamic pheromone updating[J]. Journal of Software, 2004, 15(2): 185-192.

[13] 付治政, 肖菁, 张军. 基于信息素调整的蚁群算法求解JSP问题[J]. 计算机工程与设计, 2010, 31(2): 378-381.
FU Zhi-zheng, XIAO Jing, ZHANG Jun. Implementation of ant colony system algorithm with changing pheromones for job shop scheduling problem[J]. Computer Engineering and Design, 2010, 31(2): 378-381.

(编辑 陈灿华)

收稿日期：2010-10-08；修回日期：2010-12-28

基金项目：浙江省自然科学基金资助项目(Y106460)

通信作者：王兆青(1965-)，男，浙江杭州人，博士，教授，从事网络计算、嵌入式系统的研究；电话：15550951071；E-mail：zilggjb@163.com