文章编号:1004-0609(2015)-05-1200-09
Mohr-Coulomb屈服准则与Drucker-Prager屈服准则在块体非晶合金中的应用
邹 萍,钟 鸣,龙志林,陈舒敏,廖光开,杜雪林
(湘潭大学 土木工程与力学学院,湘潭 411105)
摘 要:推导Mohr-Coulomb(M-C)和Drucker-Prager(D-P)屈服准则在不同应力状态下的表达式以及它们之间的相互关系;基于文献数据,比较两个准则描述块体非晶合金屈服行为的适应性,详细地阐述了正应力与静水压力对块体非晶合金屈服行为的影响。结果表明:静水压力对材料屈服的影响相当于一个叠加的正应力,无论是压缩还是拉伸,均对剪切屈服或断裂起抑制作用。D–P屈服准则函数描述块体非晶合晶的屈服断裂比M–C准则更好。
关键词:块体非晶合金;Mohr-Coulomb屈服准则;Drucker-Prager屈服准则;正应力;静水压力
中图分类号:TG139 +.8 文献标志码:A
Applications of Mohr-Coulomb yield criterion and Drucker-Prager yield criterion in bulk amorphous alloys
ZOU Ping, ZHONG Ming, LONG Zhi-lin, CHEN Shu-min, LIAO Guang-kai, DU Xue-lin
(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)
Abstract: The expressions and relationships of the Mohr-Coulomb (M-C) and Drucker-Prager (D-P) yield criteria under various stress states were derived firstly, and the yield behavior adaptabilities of bulk amorphous alloys described by the two criteria were compared based on the data of literatures. Finally, effects of normal stress and hydrostatic pressure on the yield behavior of BAAs were intelligently demonstrated. The results show that the influence of hydrostatic pressure on the yield behavior of BAAs is equivalent to a superposition of normal stress under tensile or compressive load, and either the shear yielding or fracture is inhibited by hydrostatic pressure; The D–P criterion is more suitable for explaining the yielding of BAAs than M–C yielding criterion.
Key words: bulk amorphous alloy; Mohr-Coulomb yield criterion; Drucker-Prager yield criterion; normal stress; hydrostatic pressure
块体非晶合金材料因其优异的力学、物理和化学性能而具有广阔的应用前景。像其他各类材料一样,在大规模工业应用前,需要细致探究非晶合金的变形和损伤的机制。不同于传统晶体材料,正应力和剪切应力均影响块体非晶合金材料的屈服和断裂行为。因此,如何构建或采用合适的本构模型描述这类长程无序而短程有序材料的屈服与断裂是目前非晶合金研究领域面临的一个重要课题[1-5]。研究人员对块体非金合金的断裂行为及特性以及非晶的合成进行了大量研 究[6-8]。陈德民[8]研究认为,块体非晶合金在不同应力状态下遵循不同的屈服准则,如在拉伸条件下遵循Mises屈服准则,而在压缩条件下遵循Mohr-Coulomb (M-C)屈服准则。基于Mises屈服准则、M-C和Drucker-Prager(D-P)屈服准则,REZAEE-BAZZAZ等[4]采用有限元分别模拟了Zr55Cu30Al10Ni5块体非晶合金的纳米压痕行为。结果表明:不同于Mises屈服准则,M-C与D-P屈服准则均能很好地预测该合金的载荷-位移曲线及压痕周围的“堆积现象”。研究人员基于自由体积理论和剪切转变区理论对块体非晶合金的屈服行为进行了讨论[9-11],一些反映非晶材料变形过程中剪胀效应的屈服准则也已经被提出,如M-C准则和D-P准则,但对于M-C准则和D-P准则如何描述正应力与静水压力对非晶合金屈服行为的影响及其适应性或优劣性仍然缺乏清晰的阐述。
本文作者首先推导了M-C准则和D-P准则在不同应力状态下的表达式以及它们之间的相互关系;然后基于文献实验和模拟数据,比较两个准则描述块体非晶合金屈服行为的适应性和优劣性;最后探讨了几何因数和应力状态对块体非晶合金材料的屈服和断裂的影响,进而阐述正应力与静水压力对块体非晶合金屈服行为的影响。
1 Mohr-Coulomb(M-C)屈服准则
在1900年,MOHR[12]提出当材料中任意点在某一方向的平面上所受的剪应力τn达到某一特定临界值时,该点就进入屈服,其表达式如式(1)所示:
 (1)
(1)
式中,σn为任意平面上的正应力(以拉为正);φ为内摩擦角;c为黏聚力,且φ和c都是材料常数,由实验确定。对于无内摩擦材料(φ=0),式(1)即为Tresca屈服条件,c是纯剪切屈服应力。当Coulomb强度直线与Mohr应力圆相切时,材料发生屈服或破坏。M-C准则在三维主应力空间(σ1、σ2和σ3为主应力)的屈服面为不规则六角形截面的角锥体表面,在π平面上的屈服轨迹为不等角的六边形。τn和σn用主应力可表示为
 (2)
(2)
 (3)
(3)
将式(2)和(3)代入式(1)中,M-C屈服条件可用主应力表示为
 (4)
(4)
 (5)
(5)
 (6)
(6)
基于式(4),单轴拉伸屈服应力(σt)和单轴压缩屈服应力(σc)计算式分别为
 (7)
(7)
 (8)
(8)
 (9)
(9)
由式(4)~(9)则M-C准则可表示为
 (10)
(10)
由式(4)可得
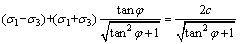 (11)
(11)
因此,M-C准则在复杂应力状态下可以表示为
 (12)
(12)
 (13)
(13)
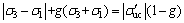 (14)
(14)
式中: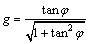 ;
; 。
。
若将主应力换成应力张量的第一不变量I1和应力偏张量的第二不变量J2及应力洛德角θσ,M-C准则可表述为

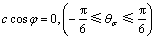 (15)
(15)
式中: ;
;
 ;
; 。
。
2 Drucker-Prager(D-P)屈服准则
在Mises屈服条件的基础上,考虑静水压力的存在,就有了Drucker-Prager(D-P)屈服准则(或广义米塞斯准则),表达式如式(16)所示:
 (16)
(16)
式中:α和k分别为与材料内摩擦角φ和黏聚力c有关的常数;不同的α和k在π平面上代表不同的圆。D-P准则在主应力空间则是一个圆锥面,在π平面上是一个圆。在偏平面上的圆半径r在数值上等于偏平面上的剪应力τπ,表达式为
 (17)
(17)
将 和
和 代入式(16),则D-P准则可表示为
代入式(16),则D-P准则可表示为
 (18)
(18)
3 D-P系列屈服准则与M-C屈服准则之间的参数关系
对式(15)中M-C准则进行变换可得

 (19)
(19)
若取θσ为常数,比较式(16)与(19),可得M-C准则的等效D-P系列准则变换的统一表达式如式(20)和(21)所示:
 (20)
(20)
 (21)
(21)
通过该关系式可以求得与M-C准则匹配的D-P系列准则对应的α和k参数。基于θσ的定义,不同的θσ可以反映材料的不同应力状态。当θσ为一定值时,α和k完全取决于c和φ,M-C屈服函数也就简化成了D-P准则,它在π平面上是一个圆。因此,θσ取不
同的值,就可以得到不同的D-P准则。不同D-P准则与M-C准则的之间的关系可以根据等效圆面积确定,从而实现两种准则的相互转换[13-14]。表1所列为不同应力状态下D-P系列准则与M-C准则的参数关系。需要说明的是,D-P系列准则能否准确描述材料的屈服行为常取决于材料的应力状态。
4 M-C屈服准则与D-P系列屈服准则在块体非晶合金中的应用
4.1 单轴应力状态
当α和k用单轴拉伸屈服应力σt和单轴压缩屈服应力σc表示时,D-P准则又可以表示为
 (22)
(22)
式中: ;
; 。
。
基于M-C准则和D-P准则,单轴拉伸、单轴压缩以及纯剪状态的屈服应力计算表达式如表2所列。由表2可以看出,M-C准则和D-P准则均能描述非晶合金的拉压强度的差异性(S-D)。D-P准则与M-C准则的之间的关系可以根据等效圆面积确定。
通过两种准则的相互转换,可以实现统一的计算。因此,在单轴应力状态下,由表1中D-P系列准则与M-C准则的参数关系可得
 (23)
(23)
 (24)
(24)
 (25)
(25)
表1 M-C屈服准则与D-P系列屈服准则的参数表达式
Table 1 Parameter expressions of M-C yield criterion and D-P yield criteria

表2 基于M-C准则与D-P准则的屈服应力表达式
Table 2 Yield stress expressions based on M-C and D-P criteria

 (26)
(26)
 (27)
(27)
 (28)
(28)
式中:σt,DP1、σc,DP1、σt,DP2、σc,DP2、σt,DP3和σt,DP3分别为基于D-P系列屈服准则DP1、DP2和DP3的单轴拉伸屈服应力和单轴压缩屈服应力的计算表达式。
表3 不同块体非晶合金在拉伸和压缩过程中不同参数的实测值及基于D-P系列准则和M-C准则的预测值
Table 3 Experimental parameters values of different bulk metallic glasses (BMGs) and predictive values based on D-P and M-C criterions in process of tension and compression

表3所列为不同合金成分块体非晶合金的拉伸断裂角(θT)、压缩断裂角(θC)、拉伸屈服或断裂应力(σt)、压缩屈服或断裂应力(σc)的实验值以及基于M-C准则(σt,M-C)和D-P系列屈服准则(DP1、DP2和DP3 )预测的拉伸屈服或断裂应力(σt,DP1、σt,DP2和σt,DP3)。图1所示为不同非晶合金通过实验测定的单轴拉伸屈服或断裂应力以及通过M-C准则和D-P系列屈服准则(DP1、DP2和DP3)预测的拉伸屈服或断裂应力。图2所示为预测的非晶合金拉伸屈服或断裂应力与实验值之差的绝对值及其平均值的对比情况。从表3及图1和2可以看出,在单轴应力状态下,DP1、DP2及M-C准则预测值与实验值相近,尤其DP1能很好地拟合实验数据;单轴压缩或单轴拉伸不满足平面应变条件,因此,DP3预测值与实验结果相差较大。

图1 基于D-P系列准则和M-C准则预测的非晶合金拉伸屈服或断裂应力与其对应的实验测量值
Fig. 1 Tensile yield or fracture stress of bulk metallic glasses predicted by D-P criteria and M-C criterion and corrosponding experimental values

图2 不同准则预测的非晶合金拉伸屈服或断裂应力与实测值之差的绝对值
Fig. 2 Absolute difference values of between experimental tensile yield or fracture stress values of amorphous alloys and predictive values based on different criterions
4.2 复杂应力状态
在室温下,块体非晶的拉伸与压缩断裂常常表现为脆性的剪切断裂。M-C准则与D-P准则都是从剪切变形的观点出发的,当任意斜截面上的剪应力达到某一极限值时,材料就发生屈服。在双轴应力或复杂应力状态下,必然存在两个较大的主剪应力或一个较大和一个较小的主剪应力,在这种复杂的应力状态下,也能使剪应力达到某一极限值,从而使材料发生剪切滑移,甚至断裂。此时,正应力与静水压力在剪切过程中所起的作用就成了值得研究的问题。
根据式(12)~(14)分别绘出两条平行线,复杂应力状态下的M-C准则仍然是一个不规则的六边形。复杂应力状态下的D-P准则如式(29)所示:
 (29)
(29)

图3 平面应力状态下不同原子数Cu-Zr非晶合金屈服行为原子模拟数据以及基于M-C准则和D-P准则拟合的对应屈服面[39]
Fig. 3 Atomistic simulation data on yield behavior of Cu-Zr amorphous alloys with different atoms under plane stress state and corresponding yield surfaces predicted by M-C yield criterion and D-P yield criterion[39]

图4 平面应力状态下不同原子数Dzugutov非晶合金屈服行为原子模拟数据以及基于M-C准则和D-P准则拟合的对应屈服面[40]
Fig. 4 Atomistic simulation data on yield behavior of Dzugutov amorphous alloys with different atoms under plane stress state and corresponding yield surfaces predicted by M-C yield criterion and D-P yield criterion[40]
式中: ;
;
 。
。
选取块体非晶合金屈服的原子模拟结果[39-40],利用M-C准则与D-P准则对平面应力状态下屈服的原子模拟数据进行拟合,其结果如图3和4所示。由式(12)~(14)可得,图3中M-C准则的c为0.986,φ为3.5°及图4中M-C准则的c为0.818,φ为6.5°;由式(22)可得,图3中D-P准则的α为0.066,k为0.889,图4中D-P准则的α为0.137,k为0.915。M-C准则与D-P准则均能很好地拟合对应块体非晶合金屈服的原子模拟结果。然而,D-P准则呈现一个更精确的描述(见图3和4)。M-C准则屈服函数具有不连续尖点,不利于块体非晶合金的数值模拟和计算。D-P准则和M-C准则之间的区别为D-P准则考虑了静水应力的影响,剪切变形不改变物体的体积,而实际上块体非金合金自由体积的重排和聚集形成剪切带使得材料的屈服发生改变。大量的研究表明,块体非金合金的剪切带的形成和扩展与合金中的自由体积密切相关[41]。M-C准则主要是解释不同块体非晶合金多样化的剪切带倾角角度,然而,膨胀系数也显著影响剪切带角。因此,在复杂应力状态下,M-C准则并不是最好的选择。
4.3 正应力与静水压力对块体非晶合金屈服行为的影响
正应力对剪切破坏面在拉伸时起促进作用,在压缩时起抑制作用[32,36]。剪切带是块体非晶合金塑性变形的显著特征,不同高径比样品表现出不同的宏观塑性,即不同的剪切带行为。在单轴压缩应力(σ1)作用实验中,加载端的面积大于样品端面的面积,在加载时会在样品两端产生具有梯度的侧向应力。高径比较大时,侧向应力对块体非晶合金的变形及断裂造成的影响很小,只有少量沿断裂方向的主剪切带;高径比较小或低于某一临界值时,侧向应力对块体非晶合金的变形及断裂影响很大,除了大量密集的主、次剪切带,剪切带之间发生密集的分叉、交割、形成割阶,造成大量剪切带滑移,在样品表面形成网状剪切带[42]。对于高径比低于某一临界值时正应力对单轴压缩试样网状剪切带的形成可以解释如下:高径比低于某一临界值的单轴压缩试样的应力状态相当于多轴应力作用;块体非晶合金是理想线弹性或弹塑性材料,多轴应力作用下其剪切带如图5所示。在多轴应力状态下,随着剪切带的不断萌生与扩展,剪切带之间发生相互交汇,扩展受到迟滞,其扩展方向可能产生改变。主控剪切带逐渐形成,随后的塑性变形集中在一条主控剪切带内,塑性变形的承载能力下降,出现应变软化现象。剪切带越多,材料的塑性变形能力越强。

图5 多轴应力下块体非晶合金剪切带示意图
Fig. 5 Schematic diagram of shear banding in bulk amorphous alloys under multiaxial stress state
静水压力是指由均质流体作用于一个物体上的压力,这是一种全方位的力,并均匀地施加在物体表面的各个部位。在静水压力(σp)作用下,非晶合金单轴拉伸(σ1)或压缩(σ3)试样中,其任一点的应力状态可表示为 或
或 ,斜面的外法线n的方向余弦为cosα、cosβ、cosγ,则该斜面上的正应力σn与剪应力τn的大小分别为
,斜面的外法线n的方向余弦为cosα、cosβ、cosγ,则该斜面上的正应力σn与剪应力τn的大小分别为
 (30)
(30)
 (31)
(31)
式(30)和(31)分别为静水压力作用下非晶合金单轴拉伸或压缩条件下试样任意斜面上的正应力σn与剪应力τn的计算表达式。因为cosγ=sinθ,并将式(30)和(31)代入式(1)可得
 (32)
(32)
 (33)
(33)
由 或
或 ,则
,则 (单轴压缩)或
(单轴压缩)或 (单轴拉伸)。由式(32)和(33)进一步可推知:静水压力与材料的断裂角以及摩擦系数并没有数值上的关联;静水压力与剪应力呈线性关系。因此,静水压力是一个叠加的正应力,正应力效应中蕴含了静水应力效应。图6所示为基于M-C屈服准则拟合的计算数据点,发现断裂面上的剪切应力与静水压力之间存在依赖关系,即无论拉伸还是压缩,静水压力对剪切屈服或破坏均起抑制作用。在单轴拉伸过程中,块体非晶合金自由体积数量的产生大于湮灭的速率,自由体积在剪切带内聚集而表现为应变软化。单轴压缩过程中,塑性形变的集中导致局部区域内自由体积增加,局部的自由体积聚集主导着非晶合金的形变行为。静水压力越大,自由体积在剪切带内聚集越多,剪切带的分支和交叉现象就越多[43]。因此,静水压力对块体非晶合金的剪切带的形成与扩展有重要影响,从而影响块体非晶合金的屈服断裂行为。
(单轴拉伸)。由式(32)和(33)进一步可推知:静水压力与材料的断裂角以及摩擦系数并没有数值上的关联;静水压力与剪应力呈线性关系。因此,静水压力是一个叠加的正应力,正应力效应中蕴含了静水应力效应。图6所示为基于M-C屈服准则拟合的计算数据点,发现断裂面上的剪切应力与静水压力之间存在依赖关系,即无论拉伸还是压缩,静水压力对剪切屈服或破坏均起抑制作用。在单轴拉伸过程中,块体非晶合金自由体积数量的产生大于湮灭的速率,自由体积在剪切带内聚集而表现为应变软化。单轴压缩过程中,塑性形变的集中导致局部区域内自由体积增加,局部的自由体积聚集主导着非晶合金的形变行为。静水压力越大,自由体积在剪切带内聚集越多,剪切带的分支和交叉现象就越多[43]。因此,静水压力对块体非晶合金的剪切带的形成与扩展有重要影响,从而影响块体非晶合金的屈服断裂行为。

图6 在单轴拉伸、单轴压缩以及静水压力(0.1~700 MPa)下非晶合金试样断裂剪切面上的正应力和切应力[23]
Fig. 6 Normal stress and shear sress acting on fracture shear plane in amorphous alloy under unaxial tension, unaxial compression and hydrostatic pressure ranging from 0.1 to 700 MPa[23]
5 结论
1) 对比不同非晶合晶单轴应力状态和复杂应力状态下M-C准则与D-P准则关于实验数据与原子模拟数据拟合的结果。结果表明:单轴拉伸应力状态下,DP2与M-C计算值相同,DP1计算值比M-C计算值更接近于实验值;在复杂应力状态下,D-P模型因为考虑了静水压力的影响,对材料的屈服描述较为精确。D-P屈服准则函数描述块体非晶合晶的屈服断裂比M-C准则更好。
2) 块体非晶合金的剪切和塑性行为取决于样品的几何和应力状态。静水压力与材料的断裂角以及内摩擦系数没有数值上的关联。静水压力对材料屈服的影响相当于一个叠加的正应力,无论是压缩还是拉伸,均对剪切屈服或断裂起抑制作用,正应力效应中蕴含了静水应力效应。
REFERENCES
[1] BREST J S, KERYYIN V, LONGERE P, YOKOYAMA Y. Insight into plasticity mechanisms in metallic glasses by means of a Brazilian test and numerical simulation[J]. Journal of Alloys and Compounds, 2014, 586: 236-241.
[2] LI J C, WEI Q, CHEN X W, HUANG F L. On the mechanism of deformation and failure in bulk metallic glasses[J]. Materials Science and Engineering A, 2014, 610: 91-105.
[3] JIANG M Q, WILDE G, CHEN J H, QU C B, FU S Y, JIANG F, DAI L H. Cryogenic-temperature-induced transition from shear to dilatational failure in metallic glasses[J]. Acta Materialia, 2014, 77: 248-257.
[4] REZAEE-BAZZAZ A, MARVI-MASHHADI M, HADDAD- SABZEVAR M. Study of mechanical deformation of Zr55Cu30Al10Ni5 bulk metallic glass through instrumented indentation[J]. Materials Science and Engineering A, 2011, 528: 6630-6635.
[5] FORNELL J, GONZALEZA S, PELLICER E, STEENBERGE N, PEREZ P, SURINACH S, BARO M D, SORT J. Deformation and fracture behavior of corrosion-resistant, potentially biocompatible, Ti40Zr10Cu38Pd12 bulk metallic glass[J]. Journal of Alloys and Compounds, 2012, 536: S74-S77.
[6] 马卫锋, 寇宏超, 李金山, 陈春生, 杜三明, 周 廉, 付恒志. 钨丝增强Zr基非晶复合材料动态力行为及断裂特性[J]. 中国有色金属学报, 2008, 18(6): 1045-1050.
MA Wei-feng, KOU Hong-chao, LI Jin-shan, CHEN Chun-sheng, DU San-ming, ZHOU Lian, FU Heng-zhi. Dynamic mechanical behaviors and fracture characteristic of tungsten fiber reinforced Zr-based metallic glass matrix composites[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(6): 1045-1050.
[7] 杨元政, 董振江, 仇在宏, 陈小祝, 谢致薇, 白晓军. 块体非晶合金Cu58Zr20Ti20Mo2的形成与力学性能[J]. 中国有色金属学报, 2007, 17(7): 1090-1095.
YANG Yuan-zheng, DONG Zhen-jiang, QIU Zai-hong, CHEN Xiao-zhu, XIE Zhi-wei, BAI Xiao-jun. Formation and mechanical properties of Cu58Zr20Ti20Mo2 bulk metallic glass[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(7): 1090-1095.
[8] 陈德民. Zr基块体非晶合金屈服行为及屈服准则研究[J]. 装甲兵工程学院学报, 2010, 24(1): 83-86.
CHEN De-min. Research on yield behavior and criterion of Zr-base bulk amorphous alloy[J]. Journal of Academy of Armored Force Engineering, 2010, 24(1): 83-86.
[9] 廖光开, 龙志林, 杨 妙, 陈舒敏, 邹 萍. 钨纤维增强锆基块体非晶复合材料的黏弹性响应[J]. 中国有色金属学报, 2014, 24(11): 2762-2769.
LIAO Guang-kai, LONG Zhi-lin, YANG Miao, CHEN Shu-min, ZOU Ping. Viscoelastic response of tungsten fiber reinforced Zr-based bulk metallic glass matrix composites[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(11): 2762-2769.
[10] 廖光开, 李乡安, 邹 萍, 陈舒敏, 龙志林. 基于均匀化方法的钨丝增强锆基块体非晶复合材料等效弹性常数预测[J]. 中国有色金属学报, 2014, 24(6):1449-1458.
LIAO Guang-kai, LI Xiang-an, ZOU Ping, CHEN Shu-min, LONG Zhi-lin. Homogenization based approach for predicting equivalent elastic constants of tungsten fiber reinforced Zr based bulk metallic glass matrix composites[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 1449-1458.
[11] WU H, LIU Y, LI K Y, ZHANG Z W. Casting effect on compressive brittleness of bulk metallic glass[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(2): 385-392.
[12] MOHR O. Welche umst nde bedingen die elastizit
nde bedingen die elastizit tsgrenze und den brucheines materials[J]. Zeitschrift des Vereins Deutscher Ingenieure, 1900, 46: 1572-1577.
tsgrenze und den brucheines materials[J]. Zeitschrift des Vereins Deutscher Ingenieure, 1900, 46: 1572-1577.
[13] 郑颖人, 赵尚毅, 李安洪, 唐晓松. 有限元极限分析法及其在边坡中的应用[M]. 北京: 人民交通出版社, 2011: 17-24.
ZHENG Ying-ren, ZHAO Shang-yi, LI An-hong, TANG Xiao-song. FEM limit analysis and its application in slope engineering[M]. Beijing: China Communications Press, 2011: 17-24.
[14] 郑颖人, 沈珠江, 龚晓南. 岩土塑性力学原理[M]. 北京: 中国建筑工业出版社, 2002: 45-61.
ZHENG Yin-ren, SHEN Zhu-jiang, GONG Xiao-nan. The principles of geotechnical plastic mechanics[M]. Beijing: China Architecture and Building Press, 2002: 45-61.
[15] BARICCO M, BASER T A, DAS J, ECKERT J. Correlation between poisson ratio and Mohr-Coulomb coefficient in metallic glasses[J]. Journal of Alloys and Compounds, 2009, 483: 125-131.
[16] INOUE A, ZHANG W, ZHANG T, KUROSAKA K. High-strength Cu-based bulk glassy alloys in Cu-Zr-Ti and Cu-Hf-Ti ternary systems[J]. Acta Materialia, 2001, 49(14): 2645-2652.
[17] DONOVAN P E. A yield criterion for Pd40Ni40P20 metallic glass[J]. Acta Materialia, 1989, 37(2): 445-456.
[18] MUKAI T, NIEH T G, KAWAMURA Y. Effect of strain rate on compressive behavior of a Pd40Ni40P20 bulk metallic glass[J]. Intermetallics, 2002, 10: 1071-1077.
[19] DAVIS L A, KAVESH S. Deformation and fracture of an amorphous metallic alloy at high pressure[J]. Journal of Materials Science, 1975, 10(3): 453-459.
[20] KIMURA H, MASUMOTO T. Plastic constraint and ductility in tensile notched specimens of amorphous Pd78Cu6Si16[J]. Metallurgical Transactions A, 1983, 14: 187-230.
[21] LEWANDOWSKI J J, LOWHAPHAUDU P. Effects of hydrostatic pressure on the flow and fracture of a bulk amorphous metal[J]. Philosophical Magazine A, 2002, 82: 3427-3441.
[22] JIANG M Q, LING Z, MENG J X, DAI L H. Energy dissipation in fracture of bulk metallic glasses via inherent competition between local softening and quasi-cleavage[J]. Philosophical Magazine, 2008, 88: 407-426.
[23] SERGUEEVA A V, MARA N A, KUNTZ J D, LAVERNIA E J, MUKHERJEE A K. Shear band formation and ductility in bulk metallic glass[J]. Philosophical Magazine, 2005, 85(23): 2671-2687.
[24] LIU C T, HEATHERLY L, EASTON D S, CARMICHAEL C A, WRIGHT J L, SCHNEIBEL J H, YOO M H, CHEN C H, INOUE A. Test environments and mechanical properties of Zr-base bulk amorphous alloys[J]. Metallurgical and Materials Transactions A, 1998, 29: 1811-1820.
[25] HE G, LU J, BIAN Z, CHEN D J, CHEN G L, TU G C, CHEN G J. Fracture morphology and quenched-in precipitates induced embrittlement in a Zr-base bulk glass[J]. Materials Transactions JIM, 2001, 42(2): 356-364.
[26] ZHANG Z F, ECKERT J, SCHULTZ L. Fatigue and fracture behavior of bulk metallic glass[J]. Metallurgical and Materials Transactions A, 2004, 35: 3489-3498.
[27] YOSHIKAWA T, TOKUDA M, INABA T. Influence of thermoplastic deformation on mechanical properties of Zr-based bulk metallic glasses at room temperature[J]. International Journal of Mechanical Sciences, 2008, 50(5): 888-896.
[28] KERYVIN V, VAILLANT M L, ROUXEL T, HUGER M, GLORANT T, KAWAMURA Y. Thermal stability and crystallisation of a Zr55Cu30Al10Ni5 bulk metallic glass studied by in situ ultrasonic echography[J]. Intermetallics, 2002, 10: 1289-1296.
[29] HIRANO T, KATO H, MATSUO A, KAWAMURA Y, INOUE A. Synthesis and mechanical properties of Zr55Al10Ni5Cu30 bulk glass composites containing ZrC particles formed by the in-situ reaction[J]. Materials Transactions JIM, 2000, 41(11): 1454-1459.
[30] GAO H L, SHEN Y, XU J. Weibull analysis of fracture strength for Zr55Ti2Co28Al15 bulk metallic glass: Tension-compression asymmetry and porosity effect[J]. Journal of Materials Research, 2011, 26: 2087-2097.
[31] OTT R T, SANSOZ F, JIAO T, WARNER D, FAN C, MOLINARI J F, RAMESH K T, HUFNAGEL T C. Yield criteria and strain-rate behavior of Zr57.4Cu16.4Ni8.2Ta8Al10 metallic- glass-matrix composites[J]. Metallurgical and Materials Transactions A, 2006, 37: 3251-3258.
[32] ZHANG Z F, HE G, ECKERT J, SCHULTZ L. Fracture mechanisms in bulk metallic glassy materials[J]. Physical Review Letters, 2003, 91: 045505.
[33] SZUECS F, KIM C P, JOHNSON W L. Mechanical properties of Zr56.2Ti13.8Nb5.0-Cu6.9Ni5.6Be12.5 ductile phase reinforced bulk metallic glass composite[J]. Acta Materialia, 2001, 49(9): 1507-1513.
[34] WU F F, ZHANG Z F, MAO S X, PEKER A, ECKERT J. Effect of annealing on the mechanical properties and fracture mechanisms of a Zr56.2Ti13.8Nb5.0Cu6.9Ni5.6Be12.5 bulk- metallic- glass composite[J]. Physical Review B, 2007, 75: 134201.
[35] INOUE A. Stabilization of metallic supercooled liquid and bulk amorphous alloys[J]. Acta Materialia, 2000, 48(1): 279-306.
[36] WU F F, ZHANG Z F. Strength asymmetry of ductile dendrites reinforced Zr- and Ti-based composites[J]. Journal of Materials Research, 2006, 21(9): 2331-2336.
[37] LEE M L, LI Y, SCHUH C A. Effect of a controlled volume fraction of dendritic phases on tensile and compressive ductility in La-based metallic glass matrix composites[J]. Acta Materialia, 2004, 52(14): 4121-4131.
[38] CONNER R D, LI Y, NIX W D, JOHNSON W L. Shear band spacing under bending of Zr-based metallic glass plates[J]. Acta Materialia, 2004, 52(8): 24-29.
[39] SCHUH C A, LUND A C. Atomistic basis for the plastic yield criterion of metallic glass[J]. Nature Materials, 2003, 2: 449- 452.
[40] VARGONEN M, HUANG L P, SHI Y F. Evaluating Mohr-Coulomb yield criterion for plastic flow in model metallic glasses[J]. Journal of Non-Crystalline Solids, 2012, 358: 3488-3494.
[41] RUITENBERG G, HEY P D, SOMMER F, SIETSMA J. Pressure-induced structural relaxation in amorphous Pd40Ni40P20: The formation volume for diffusion defects[J]. Physical Review Letters, 1997, 79: 4830-4833.
[42] 胡 静. 应力状态对大块金属玻璃剪切带行为影响的研究[D]. 湘潭: 湖南科技大学, 2011: 27-33.
HU Jing. The study on effect of stress state to shear banding behaviors in bulk metallic glasses[D]. Xiangtan: Hunan University of Science and Technology, 2011: 27-33.
[43] LIU L F, YANG J, HU J, LI H Q, GUO S B. Effect of hydrostatic pressure on shear banding behaviors in bulk metallic glasses[J]. Materials Letters, 2013, 24: 289-292.
(编辑 王 超)
基金项目:国家自然科学基金资助项目(51471139,51071134);湖南省自然科学基金重点项目(12JJ2024);湖南省研究生科研创新项目(CX2014B278)
收稿日期:2014-08-04;修订日期:2014-12-20
通信作者:龙志林,教授,博士;电话:0731-58298287;E-mail:longzl@xtu.edu.cn