J. Cent. South Univ. (2018) 25: 653-661

DOI: https://doi.org/10.1007/s11771-018-3768-x

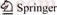
Degradation of joint surface morphology, shear behavior and closure characteristics during cyclic loading

FAN Wen-chen(范文臣)^{1, 2}, CAO Ping(曹平)¹, LONG Long(龙龙)^{1, 2}

1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: In order to investigate the failure mechanism of rock joint, a series of laboratory tests including cyclic direct shear tests under constant normal load(CNL) conditions were conducted. Morphology parameters of the rock joint surface were precisely calculated by means of a three-dimensional laser scanning machine. All test results were analyzed to investigate the shear behavior and normal displacement behavior of rock joints under CNL conditions. Degradation of rock joint surface during cyclic shear tests was also analyzed. The comparison results of the height parameters and the hybrid parameters of the joint surface during cyclic tests show that the degradation of the surface mostly happens in the first shear and the constant normal loads imposed on the joints have significant promotion effects on the morphology degradation. During cyclic shear tests, joints surfaces evolve from rough state to smooth state but keep an overall undulation. Dilatancy of rock joints degrades with the degradation of joint surface and the increase of normal loads. The closure deformation of joint is larger than that of the intact rock, and the normal stiffness increases with the increase of shearing times.

Key words: rock joint; constant normal load condition; surface morphology degradation; shear behavior; joint closure characteristic

Cite this article as: FAN Wen-chen, CAO Ping, LONG Long. Degradation of joint surface morphology, shear behavior and closure characteristics during cyclic loading [J]. Journal of Central South University, 2018, 25(3): 653–661. DOI: https://doi.org/10.1007/s11771-018-3768-x.

1 Introduction

Mechanical properties of rock joint have been an important issue since they have significant influences on the mechanical behavior of rock masses. Properties of joints such as extent, orientation, roughness, infilling and joint wall strength often are the key factors to the stability and safety of structures built in jointed rock masses.

Lots of studies have been performed to investigate the failure mechanism of rock joint [1–7]. The key constitutive law was established for rock joint under shear work, and the correlation between the shear strength of rock joints and the surface morphology had become the heading study direction of joint mechanics. Based on the direct shear test, GRASSELLI et al [8, 9] established a constitutive law considering three-dimensional surface parameters. In fact, the surface of natural rock joint is very complex and hardly replicated. In order to study the complex rough surfaces of rock joints, the fractal methods and statistics methods were utilized to describe the surface morphology [10–13]. Even now, the accurate description of the 3D surface is a difficult project. Meanwhile, the artificial joints made up of rock-like materials overcome this problem since rock joints can be made in the form of idealized saw-tooth. INDRARATNA [14–16] manufactured a series of saw-tooth joints to test the influence of the properties of joint infill on the shear behavior of rock joints, and remarkable test results were obtained. ZHU [17] used artificial joints made of high gypsum to investigate the mechanics of rock joint with different first-order and second-order asperity heights. However, the regular triangular joints cannot reflect the asperity degradation in the direct shear. In fact, the asperity degradation of joint surface is the dominant factors to the mechanical behaviors of irregular joints. Due to the difficulty in the accurate measuring of the irregular joint surface, the degradation of joint surface was seldom directly quantified even though many methods were born intending to solve this problem [18–20].

Generally, according to previous research papers [21, 22] , the joint direct shear test includes two kinds of experimental modes, the constant normal load (CNL) and the constant normal stiffness (CNS). These two loading methods can model the rock joint under different stress conditions. The tests under CNL condition are more suitable to investigate the shear behavior of rock joints in slopes, while the tests under CNL condition are more widely used to evaluate the peak shear strength in laboratory and field tests[23]. As for the rock joints existed in underground rock masses, the displacements of rock joints are usually restricted, so the stress state of joints under CNS condition is more similar with that in the underground. But in laboratory direct shear test under CNS condition, a joint specimen is often broken just after one circle of shearing. Consequently, in order to investigate the joint surface morphology degradation and the evolution of joint closure characteristics, the CNL condition was adopted to perform the direct shear tests in this study, and the asperity of rock joint surface was accurately measured by means of a 3D laser scanning machine. The relationship between the degradation of shear behaviors, closure characteristics and the degradation of the joint surface morphology was analyzed.

2 Experimental

2.1 Specimen preparation and test apparatus

The joint specimens used in the experiment were granite joint specimens. The origin shape of the specimen was cube, and the sizes were 7 cm×7 cm×7 cm. A series of Brazilian tensile tests were performed to split the cubes and manufacture artificial joint specimens, as shown in Figure 1. The mechanical parameters of granite used in the experiment were tested, elasticity modulus is 44.2 GPa, uniaxial compressive strength is 103.51 MPa, Poisson ratio is 0.24 and tensile strength is 6.82 MPa.

Figure 1 Specimen manufacture process:

A servo-controlled shear testing machine was chosen to finish direct shear tests and joint closure tests. The whole tests were conducted under the temperature condition of 20^oC. With the help of a rigid customized shear box, the shear load and normal load could be imposed on the specimen indirectly, and both loads and displacements were recorded (Figure 2). The joint surface morphology was measured by Talysurf CLI 2000, a 3D-laser scanning machine as shown in Figure 3. Through laser beam emitting and receiving, the 3D-laser scanning machine can gauge the distance between the projected point and the laser emitting point in a precision of 0.5 μm. With the specimen platform moving in two horizontal directions X and Y, series of distances of points on joints surface were gauged and recorded. The distance between neighbor joints profiles is 0.1 mm. The Talymap Gold software was used to form the joint surface morphology by orderly arranging the recorded points and then relevant morphology characters were analyzed.

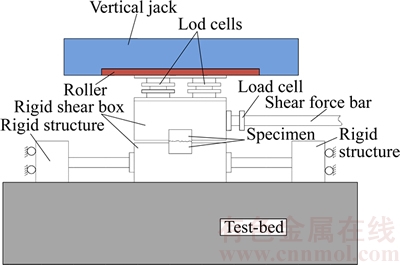
Figure 2 Direct shear test system

Figure 3 Joint surface morphology measuring system

2.2 Testing procedures

The direct shear tests were conducted under constant normal loads of 1, 2 and 3 MPa, and the shear loads were imposed on the specimen with a displacement rate of 0.9 mm/min. One shear test was regarded as completed until the shear displacement of the joint reached 6–7 mm, about 10% of the specimen size. The joint closure tests were performed in the form of uniaxial compression, and all compression tests were conducted from an initial stress level of approximately 1 kPa. To make sure the complete closure of the joints, the maximum applied stress was 30 MPa, which was equivalent to 1/3–1/2 of the uniaxial compressive strength.

3 Degradation of joint surface morphology characteristics under CNL

3.1 Morphology parameters

By means of Talymap analysis software, the joint surface morphology is analyzed. Based on the measurement result files, a series of statistical parameters of surface morphology can be output by Talymap [24–27]. All three-dimensional parameters of the joint surface are calculated related to the least-squares plane, which is defined as a plane that the quadratic sum of the distance between various points on the surface and the plane attains the minimum value. The details can be found in the user’s manual of Talymap.

The maximum peak height (S_p) is the height between the highest peak and the mean plane Eq. (1). S_pn in Eq. (1) represents the height between the highest peak point and the mean plane in the nth surface profile.

                   (1)

The maximum pit height (S_v) is the depth between the mean plane and the deepest valley as follows:

                  (2)

The maximum height (S_z) of the 3D joint surface is the height between the highest peak and the deepest valley, defined by

                             (3)

Root mean square height (S_q) is the standard deviation of the height distribution, which can reflect the mean surface roughness. It computes the standard deviation for the amplitudes of the surface (RMS):

                    (4)

where A is the definition area.

Kurtosis of the height distribution (S_ku) is the fourth statistical moment, qualifying the flatness of the height distribution.

                 (5)

The developed interfacial area ratio (S_dr) is the ratio of the increment of the interfacial area of the scale limited surface within the definition area over the definition area, defined by Eq. (6). The developed surface indicates the complexity of the surface by the comparison between the curvilinear surface and the support surface. A completely flat surface will have a S_dr near 0, and a complex surface will have a S_dr of several percent.

   (6)

Density of summits (S_ds) is expressed in peaks/mm². A point is considered as a peak if it is higher than its 8 neighbors. Arithmetic mean summit curvature of the surface (S_sc) can reflect the mean form of the peaks: either pointed or rounded, according to the mean value of the curvature of the surface at these points.

Root mean square gradient (S_dq) reflects the root-mean-square slope of the surface, can be obtained by

   (7)

The height parameters are a class of surface finish parameters which quantify the Z-axis perpendicular to the surface. The height parameters analyzed in this study include S_p, S_v, S_z, S_q and S_ku. Hybrid parameters are a class of surface finish parameters which quantify the information present on the X-, Y- and Z-axe of the surface, include S_dr, S_ds, S_sc and S_dq.

3.2 Analysis of joint surface morphology degradation

The laser scanning results of a joint surface is shown in Figure 4(a). In Figure 4(a), different colors represent different heights of the surface points, the approximate values of the colors correspond to the scale bar. The peaks and valleys can be observed obviously. It can be noticed evidently that the height between the peak points and the valleys decreases sharply from the initial state to the final state as shown in Figure 4(b). Most peak points were broken for the effect of friction during the direct shear for four times. After sheared for four times, the surface hardening was presented on the joints surface.

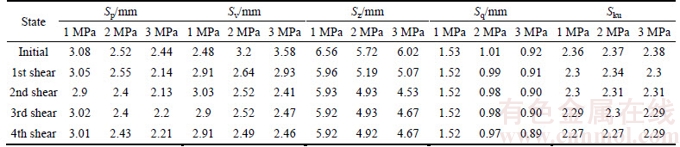
According to the height parameters listed in Table 1, the maximum heights (S_z) of the specimens under normal loads of 1, 2 and 3 MPa decreased by 9.15%, 9.26%, and 15.78% respectively after the specimens suffered the first shear, and the total decrements of S_z from the 2nd shear to the final state were 0.61%, 4.72% and 6.64%. This means that the height between the highest peak point and the deepest valley decreased significantly during the shear progress, which also indicates that the larger normal loads exert the greater effect on the degradation of joint surface morphology in the direct shear under CNL condition. The root mean square height (S_q) and Kurtosis of the height distribution (S_ku) can reflect the curvature of the joint surface profile. The decrements of S_q and S_ku indicate that the sharp parts of the joints surface were worn and the amplitude curves gradually became smoother than the initial state.

Figure 4 Degradation of surface morphology reflected in diagram:

Table 1 Height parameters of surface morphology

From Table 2, the hybrid parameters can be analyzed. The developed interfacial area ratio (S_dr) under every condition is in decreasing tendency. This indicates that the degree of roughness decreases and the case of ups and downs became more uncomplicated than that of the initial state. Under the action of the first shear, the values of S_dr of specimens reduce by 18.62%–19.22%. From the 2nd shear to the final state, the values of S_dr reduce by 4.67%–14.82%, which reflects that the destruction of the surface summits mostly happens in the first shear. Density of summits (S_ds) of the joints surfaces decreases sharply during the shear progress, especially during the first shear. The parameter S_sc reflects the mean value of the curvature of the surface. The reduction of S_sc indicates that the mean curvature of the surface decreases slightly under the action of shear friction. The parameter (S_dq) values of joint specimens under direct shear of different normal stress decrease generally. This means that the joints surfaces change from rough state to smooth state under the cyclic direct shear.

Based on this analysis referred to above, it can be concluded that the direct shear exerts significant effect on the joint surface morphology degradation, and the larger normal loads impose greater promotion effects on morphology degradation. Through comparing the height parameters and the hybrid parameters, it can be pointed out that the degradation of the surface mostly happens in the first shear.

4 Shear stress behavior in cyclic direct shear under CNL condition

4.1 Shear stress behavior

The shear stress behavior of the specimens under the normal stress 3, 2 and 1 MPa is shown in Figure 5. In the direct shear test under CNL condition, the shear stress increases with increase of shear displacement until it hits the peak, then it decreases to residual value. Similar results can be found in previous literatures [28, 8, 9]. It can be learned from the curves of shear stress– displacement in Figure 5 that the increase process of shear stress before the peak value consists of two different linearly phases. Obviously, in the former phase, the shear stress increases with the shear displacements in a relatively low rate, and increases in a larger rate in the successive phase. This is because in the former phase the resistance force in the joint surface is mainly the surface friction, and in the second phase the resistance forces of the joint are comprised of the surface friction, the shear strength of the asperity and the resistance to dilatancy.

Under the CNL conditions, the shear stress behavior mainly depends on the constant normal loads imposed on the specimens [1, 3, 29, 30]. The peak shear strengths of the joints under CNL conditions are decided by the normal loads, joint wall compressive strength (JCS) and joint roughness coefficient (JRC). To the fresh rock joints, the specimens were made through Brazilian tensile, so the JCS was equal to the uniaxial compressive strength [3]. In this study, a series of cyclic direct shear tests under CNL conditions were carried out. During the cyclic direct shear tests, the constant normal loads were kept constant in cycles under one normal load level and the JCS were all the same. The joint surface morphology was the only variate in the test. This indicates that the direct shear test under CNL condition is a good approach to studying the characteristics of the joint surface morphology and shear stress behavior.

As shown in Figure 5, the peak shear strengths of the joints in first direct shear cycle are much higher than those of the second, third and fourth direct shear cycles, meanwhile, the peak shear strength decreases with the increase of the shear cycle times. Compared with peak shear strength of the specimens in the first shear, peak shear strengths of the joint specimens dropped by 25.5%–49.16% during the second shear. In fact, there are no prominent peak points in the shear stress–shear displacement curves of the third and fourth shears. As analyzed above, most summits of the joint surface are broken and the joint roughness decreases significantly during the first shear, and the surface is changing towards smooth and hardening under the action of normal and shear stress. In the residual stage of the curves, the residual strengths of the specimens under the same normal stress were in decrease tendency from the first shear to the fourth shear, but the decrements between the values were very small, particularly in the last three shears. This indicates that the peak points behaved in the shear stress–shear displacement curves of the direct shear tests under CNL condition are due to the existing of the summits and the roughness ups and downs. The residual strength is determined by the friction of the smooth tortuous surface which does not fail in the test.

Table2 Hybrid parameters of surface morphology

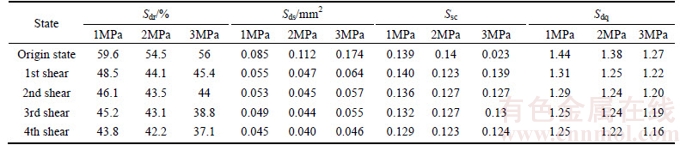
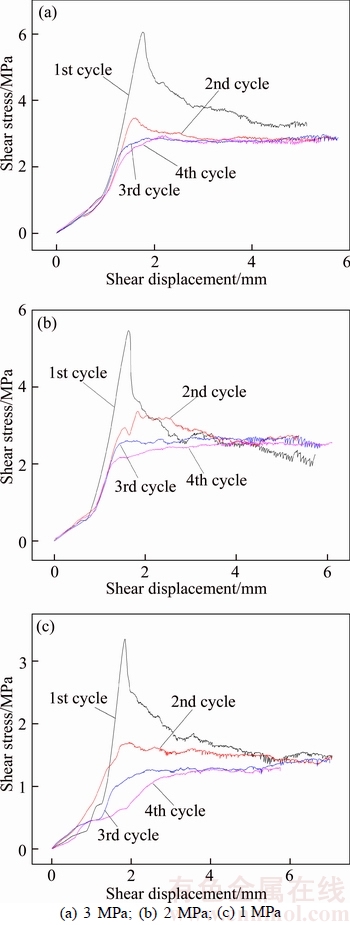
Figure 5 Shear stress vs shear displacement curves of joints under cyclic direct shear:

4.2 Dilatancy degradation during cyclic direct shear

In the joint direct shears under constant normal load condition, the dilation of the joint behaves in the mode of the increase of normal displacement during the shear progress. In this study, in order to observe the dilation in the test, the shear loads were imposed after the cease of the normal displacement. The normal displacement was reset to zero as the shear load was imposed on the specimen boundary. The normal displacement behaviors of joint specimens under various normal loads are shown in Figure 6. The normal displacement increases with the increase of shear displacement during the shear progress. By comparing the dilation under different constant normal loads, it can be concluded that as the normal loads increase, the increment of the normal displacement decreases. For the cyclic shear under a constant normal load, with the times of shear cyclic increasing, the normal displacement decreases especially from the first cyclic to the second one. This indicates that because of the degradation of the joint surface morphology during the cyclic direct shear, the joint dilation in the cyclic direct behaves in a tendency of weakening.

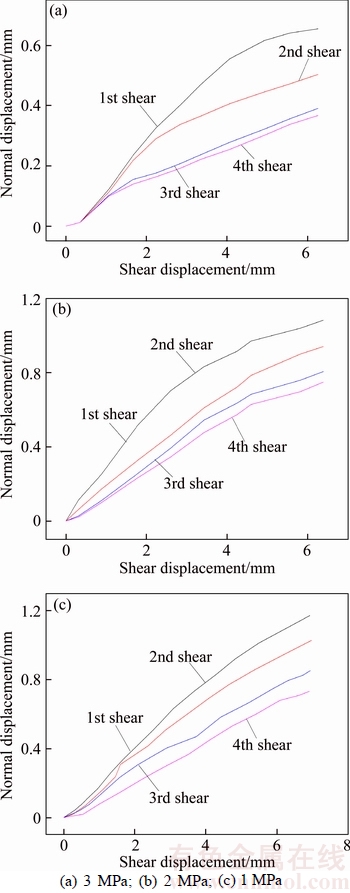
Figure 6 Behavior of normal displacement vs shear displacement curves at various normal loads:

4.3 Joint closure characteristics

Generally, most natural rock joints are unclosed, and the capacity of the normal deformation of a rock joint is mainly determined by the normal aperture and the rock property. According to the previous research, under the same normal load, the normal deformation of the joint specimen is much larger than that of the intact rock, and the normal deformation of mismatched joint is larger than that of the interlocked joint. This indicates that the joint surface morphology can be used to investigate the closure characteristics of joint.

In this study, a series of uniaxial compression tests were carried out on the joint specimens during the whole test. The closure characteristics of joints before and after shearing were observed. Figure 7 shows the closure behaviors of specimens under the uniaxial compressive stress of 30 MPa. Under the same stress, the normal deformation of the intact rock is much less than those of the joint specimens, this result is in a good agreement with test results of BARTON and BANDIS [24]. The closure deformations of the joint specimens decrease with the increase of the shear times, and the decrements of the closure deformation between the first closure and the second closure were larger than those of others.

In fact, it can be observed from Figure 4(b) that the upper face and the lower face of a fresh joint are coupled very well, but there are many spaces existing between the upper face and lower face of a joint after suffered shearing. The emergence of the spaces is because many summits of the joints are broken during the shear test. Under the compression, the contact area of the fresh coupled is a whole surface, but after the shear test the contact area of the joint reduces sharply. According to the previous analysis, as the shear times increases, the joint surface changes from the rough state to the smoother and more hardened state. All of these increase the joint normal stiffness and lead to the weakening of the capacity of the normal deformation. As a result, the closure deformation decreases with the degradation of joint surface morphology.

5 Conclusions

1) In this study, a series of laboratory tests including cyclic direct shear tests under CNL condition and joint closure tests were conducted to investigate the failure mechanism of rock joint. By the assistance of 3D laser scanning machine, the morphology of the rock joints before and after shear tests were studied. The shear behaviors of rock joint, degradation of the joint surface morphology and the closure characteristics during cyclic shear were analyzed.

2) The heights between peak points and the valleys on joint surface decrease sharply with the increase of the shear times, and the joint surface changes from rough state to smoother state. The comparison results of the height parameters and the hybrid parameters of the joint surface during cyclic tests show that the degradation of the surface mostly happens in the first shear, the constant normal loads imposed on the joints have significant promotion effects on the morphology degradation. Since most summits on joint surface are broken during the first shear progress, there are no prominent peak stress values in the sequent direct shears. As the joint dilation is decided by the normal loads and the waviness of joint surface, the dilation displacement degrades with the degradation of joint surface morphology during the cyclic direct shear test under various normal loads, and the dilation displacement decreases with the increase of normal loads. The closure deformation of joint is larger than that of the intact rock, and it decreases with the increase of shearing times. This indicates that the degradation of joints surface morphology leads to the degradation of normal deformation capacity of rock joint.

Figure 7 Comparison of closure deformation characteristics of intact rock and joint specimens after cyclic shearing under various normal loads:

References

[1] PATTON FD. Multiple modes of shear failure in rock [C]// Proceedings of the 1st Congress of International Society of Rock Mechanics. Lisbon: ISRM, 1966: 509–513.

[2] BARTON N. Review of a new shear-strength criterion for rock joints [J]. Engineering Geology, 1973, 7: 287–332.

[3] BARTON N, CHOUBEY V. The shear strength of rock joints in theory and practice [J]. Rock Mechanics, 1976, 10: 1–54.

[4] BANANOURI N, KANIMI N S, BAGHBANAN A, MOHAMADI H R. Over-consolidation effect on shear behavior of rock joints [J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 8: 83–91.

[5] PARK J W, SONG J J. Numerical method for the determination of contact areas of a rock joint under normal and shear loads [J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 58: 8–22.

[6] KHABAT A H, NIMA B, SAEED K N. The influence of asperity deformability on the mechanical behavior of rock joints [J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 70: 154–161.

[7] LI Kai-hui, CAO Ping, ZHANG Ke, ZHONG Yong-fang. Macro and meso characteristics evolution on shear behavior of rock joints [J]. Journal of Central South University, 2015, 22: 3087–3096.

[8] GRASSELLI G, EGGER P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters [J]. International Journal of Rock Mechanics & Mining Sciences, 2003, 40(1): 25–40.

[9] GRASSELLI G, WIRTH J, EGGER P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing [J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39(6): 789–800.

[10] KULATILAKE PHSW, UM J, PAN G. Requirements for accurate quantification of self-affine roughness using the variogram method [J]. International Journal of Solids and Structures, 1998, 35(31, 32): 41–67.

[11] HUANG SL, OELFKE SM, SPECK R. Applicability of fractal characterization and modelling to rock joint profiles [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics, Abstracts, 1992, 29(2): 89–98.

[12] HOMAND F, BELEM T, SOULEY M. Friction and degradation of rock joint surfaces under shear loads [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(10): 973–999.

[13] LI Yan-rong, HUANG Run-qiu. Relationship between joint roughness coefficient and fractal dimension of rock fracture surfaces [J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 75: 15–22.

[14] INDRARATNA B, HAQUE A, AZIZ N. Shear behavior of idealized infilled joints under constant normal stiffness [J]. Geotechnique, 1999, 49(3): 331–355.

[15] INDRARATNA B, WELIDENIYA H S, BROWN E T. A shear strength model for idealised infilled joints under constant normal stiffness (CNS) [J]. Geotechnique, 2005, 55(3): 215–226.

[16] INDRARATNA B, JAYANATHAN M, BROWN E T. Shear strength model for over consolidated clay-infilled idealised rock joints [J]. Geotechnique, 2008, 58(1): 55–65.

[17] ZHU Xiao-ming, LI Hai-bo, LIU Bo, ZOU Fei, MO Zhen-ze, YANG Feng-wei, HAO Ya-fei. Experimental study of shear strength of joints with first-order and second-order asperities [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1810–1818. (in Chinese)

[18] HUTSON R W, DOWDING C H. Joint asperity degradation during cyclic shear [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics, 1990, 27(2): 109–119.

[19] BELEM T, SOULEY M, HOMAND F. Modeling surface roughness degradation of rock joint wall during monotonic and cyclic shearing [J]. Acta Geotech, 2007, 2(4): 227–248.

[20] BELEM T, SOULEY M, HOMAND F. Method for quantification of wear of sheared joint walls based on surface morphology [J]. Rock Mech Rock Eng, 2009, 42(6): 883–910.

[21] MOHD M, MOHD N, SONG K I, KIM D W, CHANG I H. Evolution of joint roughness degradation from cyclic loading and its effect on the elastic wave velocity [J]. Rock Mechanics Rock Engineering, 2015. DOI: 10.1007/s00603- 015-0879-7.

[22] INDRARATNA B, HAQUE A. Experimental study of shear behavior of rock joints under constant normal stiffness conditions [J]. International Journal of Rock Mechanics & Mining Sciences, 1997, 34(3, 4): 141–154.

[23] JIANG Y, XIAO J, TANABASHI Y, MIZOKAMI T. Development of an automated servo controlled direct shear apparatus applying a constant normal stiffness condition [J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41: 275–286.

[24] BARTON N R, BANDIS S. Effects of block size on the shear behavior of jointed rock [C]// Proceedings 23rd US Rock Mechanics Symposium. Berkeley, California, 1982: 739–760.

[25] CHEN Yu, CAO Ping, CHEN Rui, YUN Teng. Effect of water–rock interaction on the morphology of a rock surface [J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47: 816–822.

[26] TSE R, CRUDEN D M. Estimating joint roughness coefficients [J]. International Journal of Rock Mechanics & Mining Sciences, 1979, 16: 303–307.

[27] MAERZ N H, FRANKLIN J A, BENNETT C P. Joint roughness measurement using shadow profilometry [J]. International Journal of Rock Mechanics & Mining Sciences, 1990, 27: 329–343.

[28] REEVES M J. Rock surface roughness and frictional strength [J]. International Journal of Rock Mechanics & Mining Sciences, 1985, 22: 429–442.

[29] BARTON N, BANDIS S, BAKHTAR K. Strength deformation and conductivity coupling of rock joints [J]. International Journal of Rock Mechanics & Mining Sciences, 1985, 22: 121–140.

[30] HAQUE A, RANJITH P G. Laboratory and numerical modelling of shear behavior of natural rock joints under CNS [C]// Proceedings of 3rd Asian Rock Mechanics Symposium. Rotterdam: Mill press, 2004: 1017–1020.

(Edited by HE Yun-bin)

中文导读

循环剪切下节理表面形貌及节理力学特性劣化规律研究

摘要：为研究岩石节理循环剪切破坏机理，对岩石节理进行3种不同的常法向荷载下的直剪试验，并对节理表面初始形貌以及剪切后的形貌采用高精度三维激光形貌扫描仪进行形貌测测试，分析节理表面形貌的劣化规律。结果表明，随着剪切次数的增加，节理表面最高点与最低点之间的垂直距离迅速减小，节理表面峰点被剪断，使得上、下节理面出现较多空隙。在节理剪切过程中，剪切荷载对节理表面形貌的劣化起主要作用，而对试件所施加的法向荷载越大则会增加节理表面形貌的劣化程度，通过对比循环剪切过程中形貌高度参数和混合参数可知，节理表面的劣化主要发生在第一次剪切过程。在循环剪切过程中，节理峰值剪切强度与残余强度均随剪切次数增加而减小，随着形貌特征的劣化，节理剪胀随着剪切次数的增加而减小。节理的闭合变形远大于完整岩石的在同等法向荷载下的变形值，而节理的法向闭合位移也随着循环次数的增加及节理表面形貌特征的劣化而逐步减小。

关键词：岩石节理；常法向加载；表面形貌劣化；剪切力行为；节理闭合特征

Foundation item: Project(51274249) supported by the National Natural Science Foundation of China; Project(2015zzts076) supported by the Explore Research Fund for Graduate Students of China; Project(201406) supported by the Hunan Key Laboratory of Coal Resources and Safe Mining Open-end Funds, China

Received date: 2016-07-29; Accepted date: 2017-12-20

Corresponding author: FAN Wen-chen, PhD; Tel: +86–15273192341; E-mail: 876514389@qq.com; ORCID: 0000-0003-0150-8343