J. Cent. South Univ. (2021) 28: 1448-1458

DOI: https://doi.org/10.1007/s11771-021-4708-8

A new nonlinear empirical strength criterion for rocks under conventional triaxial compression

XIE Shi-jie(谢世杰)¹, LIN Hang(林杭)¹, CHEN Yi-fan(陈怡帆)¹, WANG Yi-xian(汪亦显)²

1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. School of Civil Engineering, Hefei University of Technology, Hefei 230009, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021

Abstract: The failure criterion of rocks is a critical factor involved in reliability design and stability analysis of geotechnical engineering. In order to accurately evaluate the triaxial compressive strength of rocks under different confining pressures, a nonlinear empirical strength criterion based on Mohr-Coulomb criterion was proposed in this paper. Through the analysis of triaxial test strength of 11 types of rock materials, the feasibility and validity of proposed criterion was discussed. For a further verification, six typical strength criteria were selected, and the prediction results of each criterion and test results were statistically analyzed. The comparative comparison results show that the prediction results obtained by applying this new criterion to 97 conventional triaxial compression tests of 11 different rock materials are highly consistent with the experimental data. Statistical analysis was executed to assess the application of the new criterion and other classical criteria in predicting the failure behavior of rock. This proposed empirical criterion provides a new reference and method for the determination of triaxial compressive strength of rock materials.

Key words: rock mechanics; conventional triaxial compressive strength; empirical strength criterion; statistic evaluation

Cite this article as: XIE Shi-jie, LIN Hang, CHEN Yi-fan, WANG Yi-xian. A new nonlinear empirical strength criterion for rocks under conventional triaxial compression [J]. Journal of Central South University, 2021, 28(5): 1448-1458. DOI: https://doi.org/10.1007/s11771-021-4708-8.

1 Introduction

The interest in the failure behavior of rocks under complicated geological conditions has been growing as the result of an increasing number of engineering activities around the world [1-7]. Wherein, the assessment of the failure criteria of rocks is crucial to geotechnical engineering practice. Typically, there are numerous forms of failure criterion, including stress failure criterion (i.e., strength criterion), energy failure criterion, strain failure criterion, among which stress failure criteria are the most commonly used criteria in the field of rock engineering [8-11]. Consequently, the investigation on the stress failure criterion of rocks is of great practical significance for designing safe and economical structures in geotechnical engineering [12].

The existing stress failure criteria for describing the failure of materials, such as metal, rock, soil, and concrete, can be classified into three classes [13]: single-shear strength theory (SSS theory), twin-shear strength theory (TSS theory) and octahedral-shear strength theory (OSS theory). These failure criteria have been well elucidated and discussed by YU [14].Specifically for rock materials, multitudinous of stress failure criteria were proposed by researchers and experts to characterize the strength of rock during last few decades [15-18]. By fitting experimental data of intact rock on the least absolute deviation, YOU [19] compared the mathematical accuracy of 16 existing failure criteria. NASSERI et al [20] investigated the available experimental data from more than 80 intact rocks and developed a strength criterion that could explain the nonlinear strength response of isotropic intact rocks. Based on the experimental data from published literature, SINGH et al [21] first proposed a parabolic strength criterion. To standardize the failure criteria adopted in engineering applications, in “Suggested Methods for Failure Criteria”, the International Society of Rock Mechanics (ISRM) recommended the use of Drucker-Prager criterion [22], Mohr-Coulomb criterion [23], and Hoek-Brown criterion [24]. Unfortunately, these three criteria also have inherently embedded in some forms of assumption, which limits their wider application. For example, classical linear strength criteria, such as the Mohr-Coulomb criterion and the Drucker-Prager criterion, cannot be adopted to characterize the nonlinear rock strength characteristics under high normal stress condition. In addition, the Hoek-Brown criterion is more applicable in the region of brittle behaviour of rock and tends to overestimate the strength of the ductile zone [25]. And numerous experimental data [26] show that the rock strength prediction results obtained by Hoek-Brown criterion under high confining pressure are significantly higher than the experimental results.

These aforesaid ground-breaking contributions provided a deep insight into the failure theory for rock materials. However, despite significant efforts, stress failure criterion of rock maintains a subject of limited understanding. Relevant comparative studies [27, 28] show that although there are more than 40 known failure criteria in the existing literatures, there is no universal failure criterion that can best characterize the complex stress states of rock materials in various geological states. None of the existing stress failure criteria [29, 30] shows obvious advantages over other failure criteria in terms of mathematical expressions or mechanical mechanisms. Therefore, it is necessary to carry out a new and deeper research on rock failure criterion.

In this paper, based on the linearized Mohr-Coulomb criterion and the triaxial strength fitting results, a nonlinear empirical strength criterion for different types of rocks is proposed. The empirical criterion is verified by abundant triaxial test data and other typical strength criteria in the published literatures. Then, this paper conducts a concise statistical analysis of the predicted results and errors. Finally, the predictive capability of new criterion is analyzed.

2 Construction of empirical strength criterion

The Mohr-Coulomb criterion (M-C criterion) is one of the most widely adopted criteria to characterize the rock failure performance. According to the linearized Mohr-Coulomb criterion, the linear relationship between triaxial compressive strength (σ₁ at failure) and confining pressure (σ₃) was given by:

                             (1)

where c and f are the cohesion and internal friction angles of rocks respectively; k and b are the material parameters that are respectively the slope and intercept of the compressive strength-confining pressure curve.

The linear M-C criterion uses only a linear failure envelope, which makes it more consistent with the typical failure line at low confining pressures. However, as shown in Figure 1, the gradient of typical failure envelope tends to decline under higher confining pressures, which means that with the increase of confining pressures, the increase rate of rock strength gradually declines [31, 32]. In this case, the linear M-C criterion is inaccurate to characterize rock failure under higher confining pressures.

In this paper, to make up for the accuracy of linear M-C criterion, an exponential form is introduced in an attempt to modify the linear M-C criterion and is further improved to describe the nonlinear characteristics of triaxial compressive strength. The specific measures are as follows:

Figure 1 Schematic diagram of linear M-C criterion overestimating triaxial compressive strength under high confining pressure

An intermediate variable was introduced:

                        (2)

Take Eq. (2) as a quadratic equation with one unary variable (where the independent variable is X), and its two roots are:

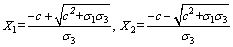       (3)

According to the definition of X, it can be known that X>0, therefore, X₂ term is omitted, namely:

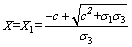                     (4)

It is easy to see: 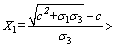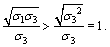Referencing to the method of YAO [33] in a guesswork way:

                             (5)

where A and B are the fitting parameters.

Substituting Eq. (5) into Eq. (2) produces

        (6)

where A and B are model parameters, which can be obtained by fitting the conventional triaxial test results.

When σ₃=0, the relationship between uniaxial compressive strength σ_1c and parameters A and c can be obtained from Eq. (6) as:

                                (7)

In fact, a strength criterion is usually phenomenological, because few strength criteria for brittle materials can be derived from rigorous mechanics [34, 35]. Most of the existing strength criteria also are generalizations of the experimental results obtained from a limited number of conventional triaxial compressive tests. The success of a strength criterion should be evaluated by its application. In the following sections, the test results are used to verify the correctness of the proposed criterion (Eq. (6)).

3 Verification of proposed empirical criterion

To prove the performance of the proposed empirical criterion, it is necessary to use reliable triaxial test data to verify the predictive capabilities of the criterion. Based on the test results from published articles [36-43], a series of conventional triaxial test data (86 tests) corresponding to 10 types of rocks were selected to examine the predictive performance of the proposed empirical criterion. For each test data, its confining pressure (σ₃) and triaxial compressive strength (σ₁ at failure) are presented in Table 1.

These test results are fitted according to the proposed empirical criterion (Eq. (6)), and the fitting curves are displayed in Figures 2-6. It can be seen from Figures 2-6 that the proposed empirical criterion well captures the nonlinear variation of triaxial compressive strength (σ₁ at failure) with confining pressure (σ₃).

According to the fitting results from Figures 2-6, the expressions of proposed empirical criterion, fitting parameters (A, B, c) and the regression R-square (R²) value are all presented in Table 2. Applicable results of collected test data demonstrated that the proposed empirical criterion shows great applicability to different rock materials. A higher regression R-square (R²) also indicates that this criterion can truly reflect the nonlinear variation law of rock triaxial compressive strength (σ₁ at failure) with confining pressure (σ₃).

4 Comparison of various criteria

To objectively assess the effectiveness and efficiency of the proposed empirical criterion in predicting the triaxial compressive strength, a test case [44] (Indiana limestone) was studied and the test results are shown in Table 3.

Table 1 Triaxial test results of different rocks

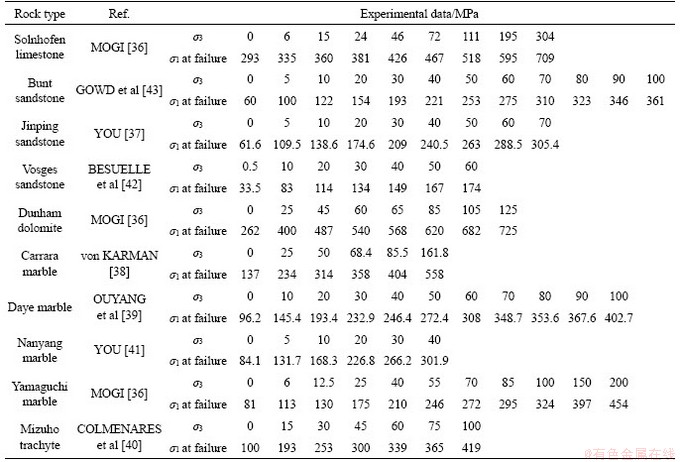
Figure 2 Failure envelopes fitted by proposed empirical criterion for Solnhofen limestone [36]

Six different criteria are widely employed in engineering practice: Mohr–Coulomb criterion (M-C criterion), Hoek-Brown criterion (H-B criterion), negative power criterion (N-P criterion) [45], modified Mohr–Coulomb criterion (MM-C criterion) [46], modified Hoek-Brown criterion (MH-B criterion) [47], exponential criterion (EXP criterion) [41] and proposed empirical criterion were used independently to predict republished triaxial compressive strength (σ₁ at failure) results. For these comparisons, four different error measurements including relative difference (D_ri), average absolute relative error percentage (AAREP, E_aar), root mean square error (RMSE, E_rms) and regression R-square value (R²), were adopted to evaluating these criteria. Equations of these error measurements are given in Eq. (8).

                 (8)

Figure 3 Failure envelopes fitted by proposed empirical criterion for sandstone:

where σ_1,pre is the predicted value by the criterion; σ_1,test is the test value; N is the total test data number; σ_1,ave is the average of the test value; D_ri is a dimensionless number which demonstrates whether the failure criterion overrates or underrates the value of triaxial compressive strength (σ₁ at failure) of rocks, and the negative values of D_ri mean underestimation; E_aar is also dimensionless, which can be adopted to represent how close the predicted value is to the test value; E_rms is used to evaluate the variation degree of data; R² is a dimensionless number to measure the fitting performance of the criterion, ranging from 0 to 1. The higher the value of R, the better the fitting effect. Besides, the smaller the values of D_ri, E_aar, and E_rms, the more accurate the corresponding criteria.

Figure 4 Failure envelopes fitted by proposed empirical criterion for dolomite [36]

Taking the proposed empirical criterion as an example to illustrate the process of solving the specific criterion expression of the listed seven criteria. By substituting the test data in Table 3 into Eq. (8), the expressions of fitting parameters A, B and c can be obtained. The fitting results are shown in Figure 7. Finally, the corresponding criterion expression is as follows:

           (9)

The M-C, H-B, MH-B and other criteria were expressed in the same way, and the specific mathematical expressions of the six criteria for the Indiana limestone test were obtained as follows:

Mohr-Coulomb criterion (M-C criterion):

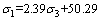                        (10)

Hoek-Brown criterion (H-B criterion):

                   (11)

Negative power criterion (N-P criterion):

             (12)

Modified Mohr–Coulomb criterion (MM-C criterion):

Figure 5 Failure envelopes fitted by proposed empirical criterion for Marble:

Figure 6 Failure envelopes fitted by proposed empirical criterion for trachyte [40]

  (13)

Modified Hoek-Brown criterion (MH-B criterion):

                  (14)

Exponential criterion (EXP criterion):

      (15)

The fitting results of the above seven criteria to the experimental results are shown in Figure 8.

The calculation results of the aforementioned seven criteria (Eqs. (9)-(15)) and the test results of conventional triaxial compressive tests are given in Figure 9.

In addition, Table 4 sums up the relative difference between the calculated results of seven criteria and test results. It can be seen from Table 4 that the triaxial compressive strength predicted by the new criterion and exponential criterion are basically consistent with the real magnitude of rock.

When the proposed empirical criterion and experimental data were statistically analyzed, it was found that the values of AAREP, RMSE and R² were 1.4%, 1.49 and 0.998, respectively. In contrast, the values of AAREP, RMSE and R² values calculated using another criterion are 15.77%, 28.79 and 0.736 (M-C criterion), 12.88%, 23.98 and 0.79 (H-B criterion), 3.5%, 6.59 and 0.97 (N-P criterion), 1.96%, 2.26 and 0.995 (MM-C criterion), 3.09%, 4.401 and 0.983 (MH-B criterion), respectively. Obviously, the proposed method performs better in estimating the triaxial compressive strength (σ₁ at failure) of rocks to some extent.

Table 2 Matches between proposed empirical criterion and conventional triaxial test data

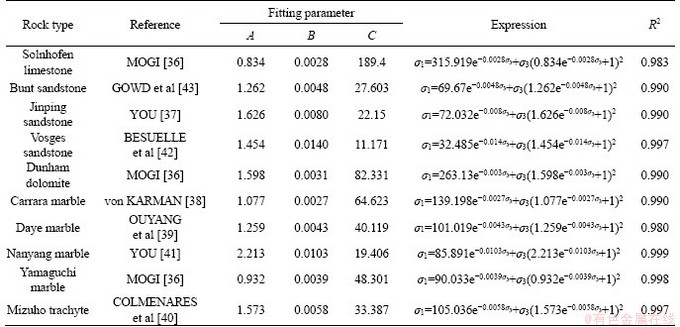
Table 3 Experimental data from conventional triaxial compression tests of Indiana limestone [44]

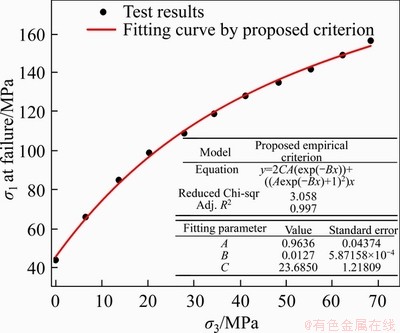
Figure 7 Proposed empirical criterion used to match test results [44] from conventional triaxial compressive tests on intact Indiana limestone

Figure 8 Fitting curves using seven criteria for test results of Indiana limestone [44]

Figure 9 Measured triaxial compressive strength of samples and calculated values of various criteria

Table 4 Test and estimated values of triaxial compressive strength and estimation errors

Figure 10 illustrates the comparison of relative difference (D_ri) in predicting test data using different criteria.

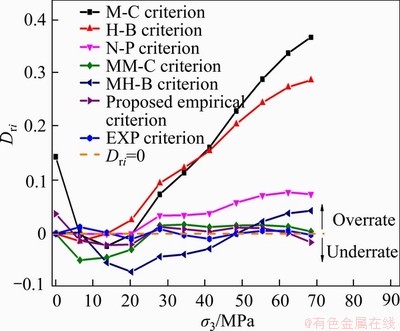
Figure 10 Representation of relative difference calculated for test data

The results presented in Figure 10 show that, as expected, the proposed empirical criterion significantly improves the estimation efficiency of triaxial compressive strength (σ₁ at failure) of rocks. In fact, the prediction error of the other three typical criteria (M-C criterion, H-B criterion, N-P criterion) gradually increases by increasing the confining pressure (σ₃), which means that the prediction ability of those criteria tends to decline under the condition of higher confining pressure(σ₃).

5 Conclusions

Based on the classical Mohr-Coulomb criterion, a new nonlinear empirical strength criterion for rocks is proposed. This criterion can accurately describe the nonlinear relationship between triaxial compressive strength and confining pressure. After a comprehensive comparison and analysis with the predicted results of the triaxial compressive test strength of 11 different rock materials and five other typical strength criteria, the following conclusions are obtained.

1) The predicted values of the proposed empirical criterion show significant consistency with the triaxial strength test values of 11 types of rock materials in the published literatures, and the correlation coefficients are all greater than 0.98, which indicates a great capacity in characterizing the nonlinear triaxial strength at high confining pressures. This demonstrates that the new strength criterion can well predict the strength values of different rock materials and has universal applicability.

2) By comparing the proposed strength criterion of this paper with six other typical strength criteria, various error statistical parameters illustrate that the accuracy of the prediction of the strength of the rock with this new criterion is far better than those failure criteria commonly adopted in geotechnical engineering: the Mohr-Coulomb, the Hoek-Brown, the negative power, the Modified Mohr-Coulomb and Modified Hoek-Brown criteria. The new criterion in this paper has a prediction effect close to that of exponential criterion. In addition, the criterion proposed in this paper effectively solves the application limitations of the linear M-C criterion, which makes it more convenient for engineering application. All these indicate that the predictive capabilities of the proposed empirical criterion are superior to those of other typical criteria.

Contributors

The overarching research goals were developed by LIN Hang and XIE Shi-jie, CHEN Yi-fan provided the experiment data, and analyzed the experiment data, WANG Yi-xian analyzed the calculated results. The initial draft of the manuscript was written by XIE Shi-jie and CHEN Yi-fan. All authors replied to reviewers’ comments and revised the final version.

Data availability statement

Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.

Conflict of interest

All the authors state that there is no conflict of interest.

References

[1] ZHANG K, LI N, LIU W L, XIE J B. Experimental study of the mechanical, energy conversion and frictional heating characteristics of locking sections [J]. Eng Fract Mech, 2020, 228: 106905. DOI: https://doi.org/10.1016/j.engfracmech. 2020.106905.

[2] XIE Shi-jie, LIN Hang, WANG Yi-xian, CAO Ri-hong, YONG Rui, DU Shi-gui. Nonlinear shear constitutive model for peak shear-type joints based on improved Harris damage function [J]. Archives of Civil and Mechanical Engineering, 2020, 20(3): Article number 95. DOI: 10.1007/s43452-020-00097-z.

[3] YANG S Q, YIN P F, ZHANG Y C, CHEN M, ZHOU X P, JING H W, ZHANG C Y. Failure behavior and crack evolution mechanism of a non-persistent jointed rock mass containing a circular hole [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 114: 101-121. DOI: 10.1016/ j.ijrmms.2018.12.017.

[4] LIN Q B, CAO P, CAO R H, LIN H, MENG J J. Mechanical behavior around double circular openings in a jointed rock mass under uniaxial compression [J]. Archives of Civil and Mechanical Engineering, 2020, 20(1): Article number 19. DOI: 10.1007/s43452-020-00027-z.

[5] ZUO J P, CHEN Y, LIU X L. Crack evolution behavior of rocks under confining pressures and its propagation model before peak stress [J]. Journal of Central South University, 2019, 26: 3045-3056. DOI: 10.1007/s11771-019-4235-z.

[6] SHI G C, CHEN G, PAN Y T, YANG X L, LIU Y, DAI G Z. Stress-drop effect on brittleness evaluation of rock materials [J]. Journal of Central South University, 2019, 26: 1807-1819. DOI: 10.1007/s11771-019-4135-2.

[7] LIN Q B, CAO P, MENG J J, CAO R H, ZHAO Z Y. Strength and failure characteristics of jointed rock mass with double circular holes under uniaxial compression: Insights from discrete element method modelling [J]. Theoretical and Applied Fracture Mechanics, 2020, 109: 102692. DOI: 10.1016/j.tafmec.2020.102692.

[8] MENG M, CHEN P J, REN R. Statistic evaluation of failure criteria in wellbore stability with temperature effects [J]. Fuel, 2019, 252: 730-752. DOI: 10.1016/j.fuel.2019.04.110.

[9] ZHANG C Y, LIN H, QIU C M, JIANG T T, ZHANG J H. The effect of cross-section shape on deformation, damage and failure of rock-like materials under uniaxial compression from both a macro and micro viewpoint [J]. International Journal of Damage Mechanics, 2020, 20: 1-20. DOI: 10.1177/ 1056789520904119.

[10] ZHANG C Y, ZOU P, WANG Y X, JIANG T T, LIN H, CAO P. An elasto-visco-plastic model based on stress functions for deformation and damage of water-saturated rocks during the freeze-thaw process [J]. Construction and Building Materials, 2020, 250: 118862. DOI: https://doi.org/10.1016/ j.conbuildmat.2020.118862.

[11] LIN H, LEI D X, YONG R, JIANG C, DU S G. Analytical and numerical analysis for frost heaving stress distribution within rock joints under freezing and thawing cycles [J]. Environmental Earth Sciences, 2020, 79: Article number 305. DOI：10.1007/s12665-020-09051-x.

[12] MEHRANPOUR M H, KULATILAKE P, MA X G, HE M C. Development of new three-dimensional rock mass strength criteria [J]. Rock Mechanics and Rock Engineering, 2018, 51: 3537-3561. DOI: 10.1007/s00603-018-1538-6.

[13] WANG P, QU S X. Analysis of ductile fracture by extended unified strength theory [J]. Int J Plast, 2018, 104: 196-213. DOI: 10.1016/j.ijplas.2018.02.011.

[14] YU M. Advances in strength theories for materials under complex stress state in the 20th Century [J]. Applied Mechanics Reviews, 2002, 55: 169-218.

[15] SHI X C, YANG X, MENG Y F, LI G. Modified Hoek-Brown failure criterion for anisotropic rocks [J]. Environmental Earth Sciences, 2016, 75(11): 995. DOI: 10.1007/ s12665-016-5810-3.

[16] da FONTOURA S A B. Lade and modified lade 3D rock strength criteria [J]. Rock Mechanics and Rock Engineering, 2012, 45: 1001-1006. DOI: 10.1007/s00603-012-0279-1.

[17] JIANG H. Three-dimensional failure criteria for rocks based on the hoek-brown criterion and a general lode dependence [J]. Int J Geomech, 2017, 17(8): 04017023. DOI: 10.1061/ (asce)gm.1943-5622.0000900.

[18] WU Q, KULATILAKE P. REV and its properties on fracture system and mechanical properties, and an orthotropic constitutive model for a jointed rock mass in a dam site in China [J]. Computers and Geotechnics, 2012, 43: 124-142. DOI: 10.1016/j.compgeo.2012.02.010.

[19] YOU M Q. Comparison of the accuracy of some conventional triaxial strength criteria for intact rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48: 852-863. DOI: 10.1016/j.ijrmms.2011.05.006.

[20] NASSERI M H B, RAO K S, RAMAMURTHY T. Anisotropic strength and deformational behavior of Himalayan schists [J]. International Journal of Rock Mechanics And Mining Sciences, 2003, 40: 3-23. DOI: 10.1016/s1365-1609(02)00103-x.

[21] SINGH M, SINGH B. A strength criterion based on critical state mechanics for intact rocks [J]. Rock Mechanics and Rock Engineering, 2005, 38: 243-248. DOI: 10.1007/s00603-004-0042-3.

[22] ALEJANO L R, BOBET A. Drucker–Prager Criterion [M]// ULUSAY R. The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007-2014. Cham: Springer International Publishing, 2015: 247-252.

[23] LABUZ J F, ZANG A. Mohr-coulomb failure criterion [J]. Rock Mechanics and Rock Engineering, 2012, 45: 975-979. DOI: 10.1007/s00603-012-0281-7.

[24] HOEK E, BROWN E T. Practical estimates of rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34: 1165-1186. DOI: https://doi. org/10.1016/S1365-1609(97)80069-X.

[25] RAMAMURTHY T, ARORA V K. Strength predictions for jointed rocks in confined and unconfined states [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31: 9-22. DOI: https://doi.org/10.1016/0148-9062(94)92311-6.

[26] LI X L, LI Q, YANG C, LI J. A nonlinear failure strength criterion for rocks based on the peak value of deviatoric stress from triaxial test [J]. Journal of China Coal Society, 2019, 44: 1-10. DOI: 10.13225/j.cnki.jccs.2019.0390.

[27] COMANICI A M, BARSANESCU P D. Modification of Mohr's criterion in order to consider the effect of the intermediate principal stress [J]. Int J Plast, 2018, 108: 40-54. DOI: 10.1016/j.ijplas.2018.04.010.

[28] KOLUPAEV A V. Equivalent stress concept for limit state analysis [M]// Advanced Structured Materials. Volume 86: Multi-surface criteria. Springer, 2018. DOI: 2018.10.1007/ 978-3-319-73049-3:223-56.

[29] BENZ T, SCHWAB R. A quantitative comparison of six rock failure criteria [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45: 1176-1186. DOI: 10.1016/j.ijrmms.2008.01.007.

[30] GAO F, YANG Y G, CHENG H M, CAI C Z. Novel 3D failure criterion for rock materials [J]. Int J Geomech, 2019, 19(6): 04019046. DOI: 10.1061/(asce)gm.1943-5622.0001421.

[31] LI K H, CHENG Y M, YIN Z Y, HAN D Y, MENG J J. Size effects in a transversely isotropic rock under brazilian tests: Laboratory testing [J]. Rock Mech Rock Eng, 2020, 53(6): 2623-2642. DOI: https://doi.org/10.1007/s00603-020-02058-7.

[32] WANG D J, TANG H M, SHEN P W, CAI Y. A parabolic failure criterion for transversely isotropic rock: Modification and verification [J]. Mathematical Problems in Engineering, 2019, 2019: 1-12. DOI: 10.1155/2019/8052560.

[33] YAO Meng-di. Experimental study on mechanical properties and crack propagation of thermal damaged rock [D]. Wuhan: Wuhan University, 2017. (in Chinese)

[34] LI D Y, HAN Z Y, SUN X L, ZHOU T, LI X B. Dynamic mechanical properties and fracturing behavior of marble specimens containing single and double flaws in SHPB tests [J]. Rock Mechanics and Rock Engineering, 2019, 52: 1623-1643. DOI: 10.1007/s00603-018-1652-5.

[35] LABUZ J F, ZENG F T, MAKHNENKO R, LI Y. Brittle failure of rock: A review and general linear criterion [J]. Journal of Structural Geology, 2018, 112: 7-28. DOI: 10.1016/j.jsg.2018.04.007.

[36] MOGI K. Experimental rock mechanics [M]. London, UK: CRC Press, 2006.

[37] YOU M. Three independent parameters to describe conventional triaxial compressive strength of intact rocks [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2010, 2: 350-356. DOI: https://doi.org/10.3724/SP.J.1235. 2010.00350.

[38] von KARMAN T. Festigkeitsversuche unter allseitigem druck [J]. Zeitschr ver Deutseh Ingenieure, 1911(55): 1749-1757. (in German)

[39] OUYANG Z, ELSWORTH D. A phenomenological failure criterion for brittle rock [J]. Rock Mechanics and Rock Engineering, 1991, 24: 133-153.

[40] COLMENARES L B, ZOBACK M D. A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39: 695-729. DOI: 10.1016/s1365-1609(02)00048-5.

[41] YOU M. Mechanical characteristics of the exponential strength criterion under conventional triaxial stresses [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47: 195-204. DOI: https://doi.org/10.1016/ j.ijrmms.2009.12.006.

[42] BESUELLE P, DESRUES J, RAYNAUD S. Experimental characterisation of the localisation phenomenon inside a Vosges sandstone in a triaxial cell [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37: 1223-1237. DOI: 10.1016/s1365-1609(00)00057-5.

[43] GOWD T N, RUMMEL F. Effect of confining pressure on the fracture behaviour of a porous rock [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1980, 17: 225-229. DOI: https://doi.org/10.1016/ 0148-9062(80)91089-X.

[44] HOEK E. Strength of jointed rock masses [J]. Géotechnique, 1983, 33: 187-223. DOI: 10.1680/geot.1983.33.3.187.

[45] LI B, WANG D G. Negative power rock strength criterion under conventional triaxial compression [J]. Coal Geology & Exploration, 2020, 48(2): 1-9.

[46] SINGH M, RAJ A, SINGH B. Modified Mohr-Coulomb criterion for non-linear triaxial and polyaxial strength of intact rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48: 546-555. DOI: 10.1016/ j.ijrmms.2011.02.004.

[47] SHEN J Y, JIMENEZ R, KARAKUS M, XU C S. A simplified failure criterion for intact rocks based on rock type and uniaxial compressive strength [J]. Rock Mechanics and Rock Engineering, 2014, 47: 357-369. DOI: 10.1007/s00603-013-0408-5.

(Edited by FANG Jing-hua)

中文导读

一种岩石在三轴压缩条件下的非线性经验强度准则

摘要：岩石的破坏准则是岩土工程可靠性设计和稳定性分析的关键因素。为了准确地评价不同围压条件下岩石的三轴抗压强度，本文提出了一种基于莫尔-库仑准则的非线性经验强度准则。通过分析11种岩石材料三轴试验强度，探讨了所提出准则的可行性和有效性。为进一步验证，选取了6个典型强度准则，并对各准则的预测结果和试验结果进行对比分析。对比结果表明，应用本文提出的准则对11种不同岩石材料进行97个常规三轴压缩试验，预测结果与试验结果高度一致。将本文提出的准则和其他经典准则在预测岩石破坏行为中的应用效果进行统计分析和评估，表明本文建立的经验准则可以为岩石材料三轴抗压强度的确定提供新的参考和方法。

关键词：岩石力学；常规三轴抗压强度；经验强度准则；统计分析

Foundation item: Project(51774322) supported by the National Natural Science Foundation of China; Project(2018JJ2500) supported by Natural Science Foundation of Hunan Province, China; Project(2020JGB135) supported by Degree and Postgraduate Education Reform Project of Central South University, China; Project(2018zzts209) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2020-04-22; Accepted date: 2020-09-21

Corresponding author: LIN Hang, PhD, Professor; Tel: +86-15388012911; E-mail: linhangabc@126.com; ORCID: https://orcid.org/0000-0002-5924-5163