DOI: 10.11817/j.issn.1672-7207.2017.06.012

参数变化对约束变胞机构构态变换随机性的影响

李小彭，高建卓，李加胜，李树军

(东北大学 机械工程与自动化学院，辽宁 沈阳，110819)

摘要：为了研究等效阻力梯度模型的影响因素在变胞机构的运动过程中的变化，以等效阻力梯度模型为基础，对一种常见的约束变胞机构的构态变换的随机性进行分析。研究结果表明：主动件转速、弹簧刚度、外力、外力矩和阻尼系数对约束变胞机构构态变换随机性的影响程度是依次减弱的。

关键词：变胞机构；约束变胞过程；随机构态；等效阻力梯度

中图分类号：TH112             文献标志码：A         文章编号：1672-7207(2017)06-1499-06

Effect of parameters variation on random working configurations of constraints metamorphic mechanism

LI Xiaopeng, GAO Jianzhuo, LI Jiasheng, LI Shujun

(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

Abstract: In order to study the change of factors affecting the motion of the equivalent resistance gradient model in the process of the motion of the metamorphic mechanism, the random working configurations of the constraints metamorphic mechanism were analyzed based on equivalent resistance gradient. The results show that the influence of the active speed, two spring stiffness coefficient, force, torque and damping coefficient on the randomness of the constraints metamorphic mechanism is weakened gradually.

Key words: metamorphic mechanism; constrained metamorphic process; random working configurations; equivalent resistance gradient

变胞机构的研究起源于1995年纸盒包装的研究^[1]。DAI等^[2]探讨了变胞机构的构态变换问题。PARISE等^[3]引申出变胞正交机构。DAI等^[4-5]实现了不同阶矩阵变换，该方法将变胞机构的构态变换转化为矩阵运算，对变胞机构的拓扑描述和构态变换进行了研究。LI等^[6]利用图论对变胞机构的构态变换进行了研究，得到了一些新的变胞构型。CHEN等^[7]发明了水下变胞车。DAI等^[8]探讨了变胞机构的变胞方式，并阐明了数学模型在变胞构态演变中的应用。LI等^[9]提出了经过改进的半加法器计算。李树军等^[10]提出了一种模块化构造变胞机构的新方法，系统研究变胞机构结构组成问题，并得出平面和空间的变胞机构都能用所给出的自由度为1的模块构造而成，实现了系统的设计变胞机构。李树军等^[11]提出了等效阻力梯度这一概念。张武翔等^[12]根据变胞机构的多构态特性及其约束变化特征分析结果，给出约束变化的实现方式，提出变胞运动副的设计原则，并提出了一种基于约束变化特征分析的变胞机构构型综合方法。畅博彦等^[13]以空间变胞并联仿生关节机构为例子，约束旋量原理被引入到变胞机构的构型综合的研究中，使得变胞机构的结构学的理论研究体系更加完善。本文作者分析变胞机构在构态变换过程中产生随机构态的原因，并对一种常见的变胞机构约束模型进行动态静力分析，总结了影响等效阻力梯度的主要因素。然后对约束变胞机构的构态变换的随机性进行分析，得出主动件转速、弹簧刚度、外力、外力矩和阻尼系数对约束变胞机构构态变换随机性的影响。

1  约束变胞机构模型的建立

欠驱动是常见的只有1个原动件的2自由度五杆机构 ^[14]，冗余自由度为1，机构的运动时序和构态均不确定，在运动过程中会表现为混沌运动。故可以建立约束变胞机构模型，如图1所示。

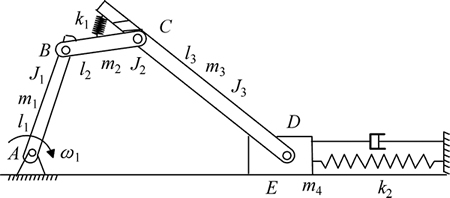
图1  约束变胞机构简图

Fig. 1  Diagram of constraints metamorphic mechanism

为了方便分析，将机构变胞前后的构态分别称为机构的第一构态和第二构态。取图2(a)所示位置为初始位置，此时，机构处于第一构态，机构等效于曲柄滑块机构；当滑块运动到图2(b)所示的位置时，滑块处于约束状态，变胞副C运动；在图2(c)位置时，机构处于第二构态，变胞副C受到的实际力大于弹簧力，机构相当于一个铰链四杆机构；在图2(d)所示位置时，变胞副C保持相对静止，当曲柄继续转动时，滑块开始运动，机构进入第一构态，如图2(e)所示。

2  约束变胞机构的随机性分析

2.1  等效阻力梯度模型

为了求解变胞机构对应的约束变胞副的约束力的变化规律，需要了解与其匹配的约束变胞副的类型及约束形式，因此，可以建立变胞运动副的阻力梯度模型^[15]。

文献[11]提到，约束变胞机构的运动过程中，每一个相对运动的变胞副都会对应一个工作构态，其余的变胞副均保持相对静止，根据变胞副提供的约束力实现了变胞副在运动与静止之间的切换。为了描述变胞副的受力情况和约束特点，并使同一机构中转动变胞副所受的约束力矩和移动变胞副所受的约束力能够进行比较，定义了量纲一的变胞运动副的等效阻力系数函数，即：

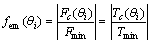          (1)

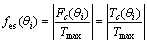          (2)

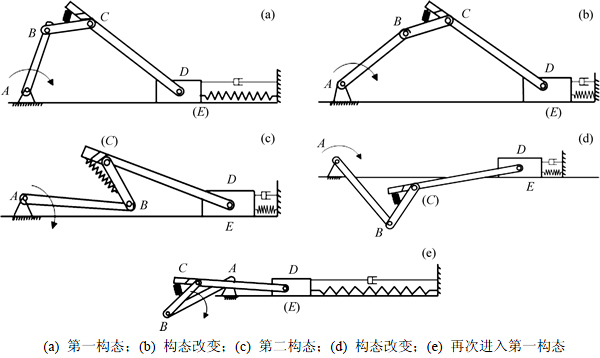
图2  约束变胞机构一个周期的运动简图

Fig. 2  A cycle movement diagram of constraints metamorphic mechanism

式中：f_em(θ_i)为相对运动变胞副的等效阻力系数函数；f_es(θ_i)为相对静止变胞副的等效阻力系数函数；F_min为变胞副最小受力；T_min为变胞副最小受力矩；F_max为变胞副最大受力；T_max为变胞副最大受力矩。

根据最小阻力原则，变胞副的动作顺序和等效阻力系数紧密相关，若要使静止变胞副的等效阻力系数大于相对运动变胞副的等效阻力系数，则等效阻力梯度的变化规律为

f_em(θ_i)≤1，f_es(θ_i)≥1            (3)

根据式(3)，等效阻力梯度曲线如图3所示。

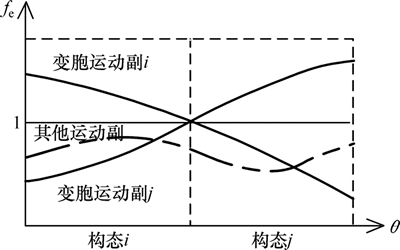
图3  等效阻力系数曲线

Fig. 3  Equivalent resistance gradient curve

2.2  构态转换过程分析

为了获得机构的初始位置参数，利用牛顿-辛普森方程，得到转动变胞副的约束角α=92.8°，第一构态与第二构态切换位置处的角位移为θ₁=66.9°，θ₂=59.6°，第一构态与第二构态切换位置处的角位移为θ₁=293.3°，θ₂=102.3°。因此，θ₁=66.9°~66.7°为第二构态区间，θ₁=-66.7°~293.1°为第一构态区间，同时对约束变胞机构进行动态静力分析。

等效系数函数的公式为

     (4)

当机构处于第一构态时，只需要判断变胞副C是否变胞即可判断机构运动过程是否会产生随机构态。因此当△T＞0时有

             (5)

当f_e(θ_i)＞1时，变胞副处于约束状态；当f_e(θ_i)＜1时，变胞副发生变胞，机构出现随机构态。当ΔT＞0时，机构受几何约束的作用，约束力矩为无穷大，此时f_e(θ_i)=∞，转动变胞副C处于约束状态，构态稳定。

当机构处于第二构态时，只需要判断变胞副E是否变胞即可判断机构运动过程是否会产生随机构态。因此当R₄＜|F_k2|时，机构有向左的运动趋势时，弹簧力在运动方向提供的力不再是约束力，因此有

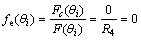           (6)

则此时机构中两变胞副同时发生变胞，机构出现随机构态。当R₄＞|F_k2|时，机构有向右的运动趋势，几何约束提供无穷大的约束力，则f_e(θ_i)=∞，变胞副处于约束状态，构态稳定。

3  不同参数对随机构态的影响

3.1  主动件转速的影响

选取机构参数如下：l₁=60 mm，l₂=30 mm，l₃=150 mm，m₄=0.2 kg，r=15 mm，a=15 mm，b=25 mm，l=185 mm，k₁=30 N/mm，k₂=1 N/mm，g=9.8 N/m²，无外力和外力矩作用。对主动构件转速ω₁分别取20，50和80 rad/s，观察等效系数函数曲线，如图4所示。从图4可见：当ω₁=20 rad/s时，变胞副C在第一构态时为约束状态，变胞副E在第二构态时也为约束状态。机构在运动过程中没有出现随机构态。当ω₁=50 rad/s时，变胞副C在第一构态保持时出现随机构态，变胞副E在第二构态时一直处于约束状态。当主动件转速ω₁=80 rad/s时，机构在t=0.034 s进行构态变换时出现随机构态，在t=0.070 s的构态保持过程中也出现了随机构态；变胞副E在t=0.01 s时出现随机构态，之后变为约束状态。由此可以得出，主动件转速对第一构态和第二构态均会产生比较大的影响，转速越大，变胞机构在运动过程中越容易出现随机构态。

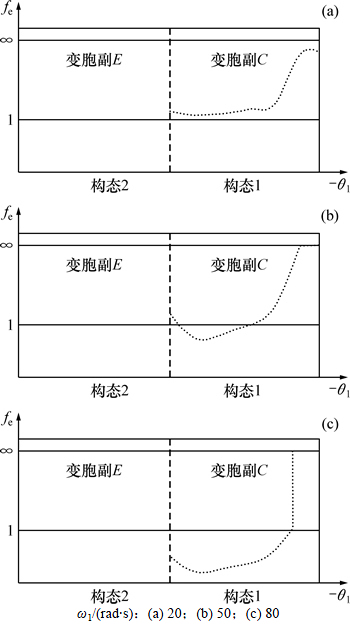
图4  不同主动件转速时等效系数函数曲线

Fig. 4  Equivalent resistance coefficient curve with different ω₁

3.2  弹簧刚度系数的影响

对弹簧的刚度系数k₁和k₂取不同值时观察等效系数函数曲线如图5所示。对比分析可知，当仅减小弹簧1的刚度系数k₁时，机构在第一构态保持过程中一直处于约束状态，在第二构态的变换和保持过程中均出现随机构态；当减小弹簧1的刚度系数k₁，增大弹簧2的刚度系数k₂时，机构在第一构态保持过程中一直处于约束状态，在第二构态的变换和保持过程中均出现随机构态，对第一构态和第二构态均有较大的影响。

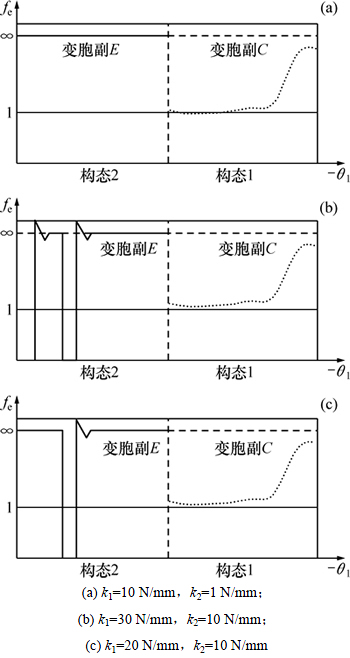
图5  不同弹簧刚度的等效系数函数曲线

Fig. 5  Equivalent resistance coefficient curve with different k₁ and k₂

3.3  外力作用的影响

其他几何参数与前文的参数相同，外力作用点为所在构件的质心，对构件CD质心处施加不同的外力F时观察等效系数函数曲线，如图6所示。由对比分析可知，当构件CD受到向下的干扰力时，对机构的第一构态影响较大，易出现随机构态；当构件CD受到向上的干扰力时，机构在第二构态保持过程中易出现随机构态。

3.4  有外力矩作用时的等效阻力梯度分析

主动件转速ω₁=20 rad/s，其他几何参数与前文的参数相同。在构件CD上施加不同的外力矩M时，观察等效系数函数曲线，如图7所示。在构件CD上施加力矩M=2 N·m时，变胞副C在第一构态的构态保持过程中出现随机构态，变胞副E一直处于约束状态。在构件CD上施加力矩M=-2 N·m时，机构在第一构态和第二构态的构态变换和保持过程中均处于约束状态。在构件BC上施加力矩M=4 N·m时，机构在第一构态的构态变换和构态保持过程中均出现随机构态，变胞副E一直处于约束状态。在构件CD上施加力矩M=-4 N·m时，变胞副C在第一构态的构态保持过程中一直处于约束状态，机构在第二构态的保持过程中出现随机构态。对比分析可知，无论构件CD上受到顺时针转矩干扰还是逆时针转矩干扰，对机构运动都有较大影响，在第一构态和第二构态的变换和保持过程中易使机构出现随机构态。

3.5  改变阻尼系数时的等效阻力梯度分析

阻尼元件(或阻尼器)对于外力作用的影响，表现为其端点的一定的速度。与运动速度成正比的阻尼称为黏性阻尼，对于黏性阻尼，F_d是速度的线性函数，即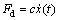，阻尼系数c是阻尼器产生单位速度所需要施加的力。不同阻尼系数的等效系数函数曲线如图8所示。

对比分析可知，阻尼系数的变化对机构在第一构态和第二构态的变换和保持过程中的运动的影响较小。

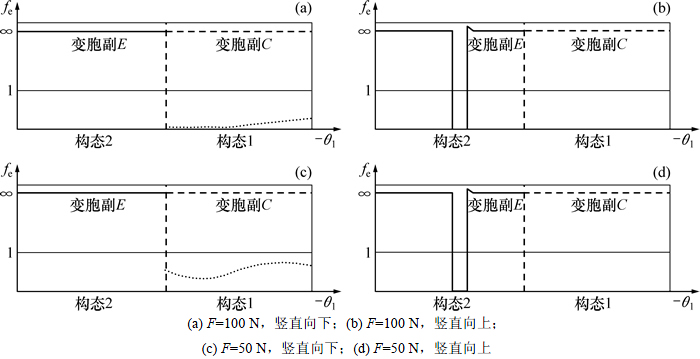
图6  在构件CD质心位置施加外力时的等效系数函数曲线

Fig. 6  Equivalent resistance coefficient curve with force on components CD centroid position

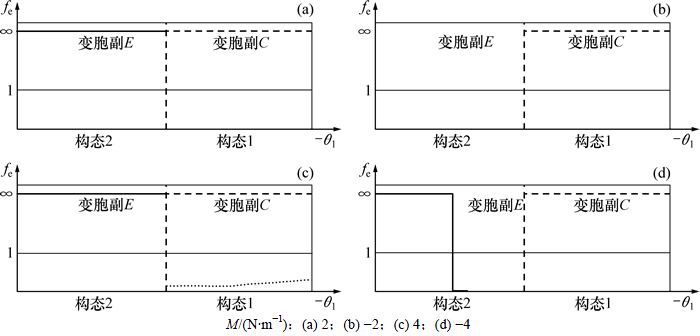
图7  不同外力矩的等效系数函数曲线

Fig. 7  Equivalent resistance coefficient curve with different torque

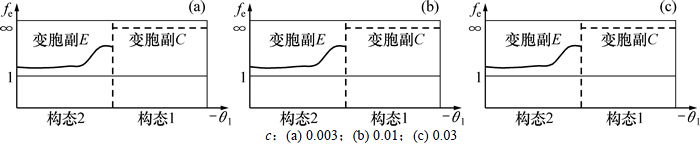
图8  不同阻尼系数的等效系数函数曲线

Fig. 8  Equivalent resistance coefficient curve with different damping coefficient

4  结论

1) 主动件转速对第一构态和第二构态均会产生比较大的影响，转速越大，变胞机构在运动过程中越容易出现随机构态。

2) 当仅减小弹簧1的刚度系数k₁时，机构在第一构态保持过程中一直处于约束状态，在第二构态的变换和保持过程中均出现随机构态；当减小弹簧1的刚度系数k₁，增大弹簧2的刚度系数k₂时，机构在第一构态保持过程中一直处于约束状态，在第二构态的变换和保持过程中均出现随机构态，对第一构态和第二构态均有较大的影响。

3) 当构件CD受到向下的干扰力时，对机构的第一构态影响较大，易出现随机构态；当构件CD受到向上的干扰力时，机构在第二构态的保持过程中易出现随机构态。无论构件CD上受到顺时针转矩干扰还是逆时针转矩干扰，对机构运动都有较大影响，在第一构态和第二构态的变换和保持过程中易使机构出现随机构态。阻尼系数的变化对机构在第一构态和第二构态的变换和保持过程中的运动的影响较小。

参考文献：

[1] DAI J S. Conceptual study of the Dexterous Reconfigurable Assembly and Packaging System[R]. Bedford: Science and Technology Report, 1996.

[2] DAI J S, REES J J. Configuration transformations in metamorphic mechanisms of foldable/erectable kinds[C]//Proc of 10th World Congress on the Theory of Machines and Mechanisms. Oulu: University of Oulu, 1999: 542-547.

[3] PARISEJJ,HOWELLLL,MAGLEBY S P. Ortho-Planar linear-motion spring[J]. Mechanism and Machine Theory, 2001,36(12): 1281-1299.

[4] DAI J S, ZHANG Q X. Metamorphic mechanisms and their configuration models[J]. Chinese Journal of Mechanical Engineering, 2000, 13(3): 212-218.

[5] YAN H S, KUO C H. Topological representations and characteristics of variable kinematic joints[J]. Transactions of the ASME, Journal of Mechanical Design, 2006, 128(2): 384-391.

[6] 李端玲, 戴建生, 张启先, 等. 基于构态变换的变胞机构结构综合[J]. 机械工程学报, 2002, 38(7): 12-16.

LI Duanling, DAI Jiansheng, ZHANG Qixian, et al. Structure synthesis of metamorphic mechanisms based on the configuration transformations[J]. Chinese Journal of Mechanical Engineering, 2002, 38(7): 12-16.

[7] CHEN Y M, LI H S, CATHALA A. Mechatronic design and locomotion of Amoebot: a metamorphic under water vehicle[J]. Journal of Robotic Systems, 2003, 20(6): 307-314.

[8] DAI J S, REES J J. Matrix representation of topological changes in metamorphic mechanisms[J]. Transactions of ASME，Journal of Mechanical Design, 2005, 127(4): 837-840.

[9] LI Duanling, ZHANG Zhonghai, DAI Jiansheng, et al. Configuration based improved synthesis of metamorphic mechanisms[C]//Proceedings of the ASME 2009 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (IDETC/CIE 2009), 33rd Mechanisms and Robotics Conference (MECH). San Diego: ASME, 2009: 1-10.

[10] 李树军, 戴建生. 基于扩展Assur杆组的变胞机构组成原理[J]. 机械工程学报, 2010, 46(13): 22-30.

LI Shujun, DAI Jiansheng. Structure of metamorphic mechanisms based on augmented assur groups[J]. Chinese Journal of Mechanical Engineering, 2010, 46(13): 22-30.

[11] 李树军, 王洪光, 戴建生. 变胞机构的等效阻力梯度模型及其设计方法[J]. 机械工程学报, 2014, 50(1): 18-23.

LI Shujun, WANG Hongguang, DAI Jiansheng. The equivalent resistance gradient model of metamorphic mechanisms and the design method[J]. Chinese Journal of Mechanical Engineering, 2014, 50(1): 18-23.

[12] 张武翔, 丁希仑, 戴建生. 基于约束变化特征分析的变胞机构构型综合方法[J]. 机械工程学报, 2013, 49(5): 1-8.

ZHANG Wuxiang, DING Xilun, DAI Jiansheng. Method for configuration synthesis of metamorphic mechanisms based on constraint variation[J]. Chinese Journal of Mechanical Engineering, 2013, 49(5): 1-8.

[13] 畅博彦, 金国光, 戴建生. 基于变约束旋量原理的变胞机构构型综合[J]. 机械工程学报, 2014, 50(5): 17-25.

CHANG Boyan, JIN Guoguang, DAI Jiansheng. Type synthesis of metamorphic mechanism based on variable constraint screw theory[J]. Chinese Journal of Mechanical Engineering, 2014, 50(5): 17-15.

[14] MASSA B, ROCCELLA S, CARROZZA M C, et al. Design and development of an underactuated prosthetic hand[C]// Proceedings of the ICRA. Washington: IEEE, 2002: 3374-3397.

[15] 徐亮. 约束变胞机构等效阻力梯度分析方法[D]. 沈阳: 东北大学机械工程与自动化学院, 2012: 19-21.

XU Liang. The equivalent resistance gradient analysis method of constraint metamorphic mechanism[D]. Shenyang: Northeastern University. School of Mechanical Engineering and Automation, 2012: 19-21.

(编辑  赵俊)

收稿日期：2016-07-29；修回日期：2016-10-21

基金项目(Foundation item)：国家自然科学基金资助项目(51275079，51575091)；辽宁省百千万人才工程培养经费资助项目(2014921018) (Projects(51275079, 51575091) supported by the National Natural Science Foundation of China; Project(2014921018) supported by Liaoning BaiQianWan Talents Program)

通信作者：李小彭，博士，教授，博士生导师，从事机械动力学、振动与摩擦耦合研究；E-mail：xpli@me.neu.edu.cn