DOI： 10.11817/j.issn.1672-7207.2021.04.033

基于一维卷积神经网络的地铁钢轨波磨识别方法

谢清林，陶功权，温泽峰

(西南交通大学 牵引动力国家重点实验室，四川 成都，610031)

摘要：利用轴箱振动加速度构建一种基于一维卷积神经网络(1-dimensional convolutional neural network，1-DCNN)的地铁钢轨波磨智能识别方法。提出“空间域”切割的方法制作样本集，构建恰当的1-DCNN结构与配置参数可对输入样本集数据进行自动特征提取并学习分类。通过设置“空间窗”长度任意调节钢轨波磨智能分类时的定位分辨率。研究结果表明：提出的1-DCNN方法能有效、快速且稳定地对钢轨波磨进行智能识别与定位，在车辆复杂的运营条件及速度时变工况下仍然能保持较高的识别精度，稳定在99.20%(标准差为0.1)；与此同时，对每一条样本的识别时间均少于0.2 ms，满足钢轨波磨在线监测的时效性。

关键词：钢轨波磨；轴箱振动；深度学习；一维卷积；“空间域”切割

中图分类号：U211.5            文献标志码：A             开放科学(资源服务)标识码(OSID)

文章编号：1672-7207（2021）04-1371-09

Detection method of metro rail corrugation based on 1-dimensional convolutional neural network

XIE　Qinglin, TAO　Gongquan, WEN　Zefeng

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

Abstract: A method based on 1-dimensional convolutional neural network(1-DCNN) was developed to identify the rail corrugation intelligently using the axle box acceleration. A mean of "spatial domain" cutting was proposed to make the sample set, and an appropriate 1-DCNN structure and configuration parameters were constructed, so that the data of the input sample set could be automatically extracted and classified. In addition, by setting the length of "spatial window", the resolution of rail corrugation positioning detection could be adjusted arbitrarily. The results show that the proposed 1-DCNN method can effectively, rapidly and stably carry out intelligent identification and positioning of the rail corrugation, and maintain a high identification accuracy of 99.20% (standard deviation of 0.1) even under the complicated operating conditions and at time-varying speed of the vehicle. Meanwhile, the recognition time of each sample data is less than 0.2 ms, which can meet the requirement of online monitoring of rail corrugation.

Key words: rail corrugation; axle box vibration; deep learning; 1-DCNN; "spatial domain" cutting

由于地铁载重容量大、运行密度高，线路条件复杂(如曲线半径小、轨道结构多样化)，车辆启动与制动频繁，使轮轨相互作用加剧，钢轨波浪形磨损(简称钢轨波磨)严重^[1]。钢轨波磨会带来一系列问题，如引起车辆轨道的异常振动与噪声污染，降低车辆和轨道部件的疲劳可靠性。据文献报道，存在钢轨波磨的地铁线路在打磨前、后司机室车内噪声差异可达到近10 dB^[2]，而存在显著钢轨波磨的地铁钢轨扣件的振动加速度甚至能达到195g^[3]。此外，一些车辆轨道零部件的疲劳断裂失效与钢轨波磨有直接关系，如车辆轴箱吊耳断裂^[4]、一系钢弹簧疲劳断裂^[5]、钢轨扣件弹条断裂^[3]等。钢轨波磨严重影响车辆的安全营运并极大地增加了养护费用。目前，钢轨打磨是控制钢轨波磨最主要的手段之一，在制定打磨策略时(如打磨周期与打磨量)，提前获悉钢轨波磨状态是十分必要的，因此，对钢轨波磨进行状态监测和故障识别具有重要意义。目前，钢轨波磨的测量方法可归纳为弦测法^[6]、惯性基准法^[7]与机器视觉法^[8]3类。弦测法使用钢轨本身作为移动参考系，使测量参考的基准随钢轨高低不平顺变化而处于变化状态，造成传递函数比(测量值与实际值之比)不恒为1，导致弦测法往往不能真实可靠地测试钢轨波磨^{[7, 9]}。惯性基准法常通过轴箱加速度的二次积分来表征波磨值，其缺点是易受车轮磨耗的干扰，并且由于高通滤波器的影响，在低速工况下测量误差较大，一般仅用于大型轨检车^[10-11]。机器视觉法往往需要精密的光电摄像设备以及复杂的图像处理手段，运用庞杂的模式识别技术以进行特定的后端处理，实际应用难度较大且代价昂贵^{[8, 12]}。由于轮轨界面直接接触，列车零部件振动行为可科学直观地反映钢轨表面状态，因此，诸多专家学者基于车辆振动响应对钢轨状态进行健康监测研究^[13-17]。BOCCIOLONE等^[18]针对钢轨维护策略，研究了轴箱加速度与钢轨波磨等级之间的相关性。MOLODOVA等^[19]利用轴箱加速度信号的幅值与功率谱密度特征，对钢轨短波缺陷进行检测。SALVADOR等^[20]开展系列现场测试以获悉钢轨波磨状态，详细分析了加速度传感器的安装位置、最佳采样及滤波频率对试验的影响。WEI等^[21]提出利用构架与车体加速度信号对城市轨道交通线路的钢轨波磨进行监测，并通过上海地铁1号线的现场试验对此方法进行了验证。江航等^[22-23]结合传统的机器学习技术与车辆振动响应对钢轨波磨的智能检测方法进行了研究，通过实验与仿真的手段获得振动信号，由经验模态分解后得到本征模态函数，分别利用BP神经网络与支持向量机对钢轨波磨进行回归与分类。周志青等^[24]通过地铁实际运营车辆获取振动信号、冲击信号样本数据各1 600条，提取振动信号其各频率带的功率与冲击信号峭度，作为支持向量机的特征参数输入以识别钢轨波磨。近年来，深度学习^[25]已经在图像识别、声音识别、自然语言处理、生物信息学等领域取得了突破性进展。卷积神经网络(convolutional neural network，CNN)作为深度学习的重要分支之一^[26]，在滚动轴承^[27]、齿轮箱^[28]、航空发动机^[29]等机械故障诊断研究领域得到应用。鉴于此，本文作者使用深度学习在机械故障诊断领域研究的基础上^[30]，结合CNN与轴箱加速度对钢轨波磨进行智能检测，以期克服现有钢轨波磨在线监测方法中的不足。本文作者定义“空间域”的概念对实测轴箱振动信号进行分割，建立振动信号与钢轨波磨的非线性映射关系，制定可供钢轨波磨智能分类的数据集；同时为充分利用CNN强大的自我学习能力，并且不破坏原始输入信号的生态信息，提出一种基于一维输入信号的钢轨波磨识别模型即一维卷积神经网络(1-dimensional convolutional neural network，1-DCNN)。

1  卷积神经网络基本理论

CNN是由哺乳动物视觉皮层细胞感受野启发而建立的一种典型的前馈神经网络，其稀疏连接与权值共享等特性可以显著减少网络参数并避免算法过拟合，最终获得输入数据的平移、旋转及缩放不变的特征表示，具有较强的鲁棒性和泛化能力。传统的CNN模型通常包含特征提取和识别分类2部分，其中特征提取阶段由卷积层和池化层交替进行。

1.1　卷积层

卷积层由多个特征图组成，1个特征图对应1个卷积核，卷积核与上一层传递的特征矢量局部区域相连，即稀疏连接。每个卷积核作用于局部感受野，通过预设的移动步长遍历全部感受野，以对各输入特征完成卷积操作，提取特征并输出至下一层。此外，各卷积核的参数在同一输入特征图与同一输出特征图之间共享。在卷积层中，每一层的输出对应多输入的卷积结果，其数学模型可以简述为

(1)

式中：i与j分别为输入和输出特征的位置变量；l为第l层网络；k为网络层数；运算符*表示对各层输入变量与权重变量进行卷积运算，对应得到第l个输出特征映射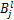；表示偏置项。在CNN中，往往会在卷积层后施加非线性层，本文使用修正线性单元(rectified linear units，ReLU)作为激活函数，以提高网络稀疏性并抑制过拟合，进一步加速CNN收敛，其函数表达式为

(2)

式中：为卷积层计算后的输出值，即送往非线性激活层的输入值。

1.2　池化层

池化层是上一层数据的缩放映射，将某处神经元感知域内的总体统计特征变量作为该神经元的输出变量。池化层的下采样属性可以加快网络计算速度，同时对过拟合有一定抑制作用。针对池化层，有N个神经元输入就有N个神经元输出，假设为第l层池化层的第j个神经元变量，其产生过程如下式所示(其中pooling( )为某一规则下的池化函数)：

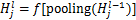(3)

实际应用中常采用最大池化算子，它给出输入特征相邻矩形区域内的最大值，数学表达式为

(4)

式中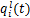：为第l层第i个特征矢量中第t个神经元的激活值；K为池化区域宽度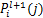；为第l层的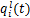经最大池化后送往第l+1层进行下一步运算的神经元对应值。

1.3　分类层

CNN的分类阶段由2个全连接层组成。其中第一个全连接层实现“展平”操作，将所有卷积池化操作后的特征矢量首尾连接，整合为一维向量；第二个全连接层的神经元数量与故障类别数目保持一致。常见的二元分类问题多利用sigmoid函数实现目标输出类别，其表达式如下：

(5)

式中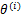：(1≤ i ≤ K)是模型的参数，得到的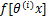即为CNN模型输出为某一类标签的概率。

2  基于1-DCNN的钢轨波磨识别流程

在图像识别领域，CNN以二维平面为研究对象。将振动信号作为一维时间序列，设计合理的1-DCNN结构显然更适于提取输入信号的特征信息。

基于1-DCNN对钢轨波磨进行状态识别时分为5个步骤：1) 信号采集与“空间域”切割；2) 振动-波磨信号非线性映射；3) 样本集建立；4) 1-DCNN结构设计与训练；5) 钢轨波磨状态识别，识别流程如图1所示。

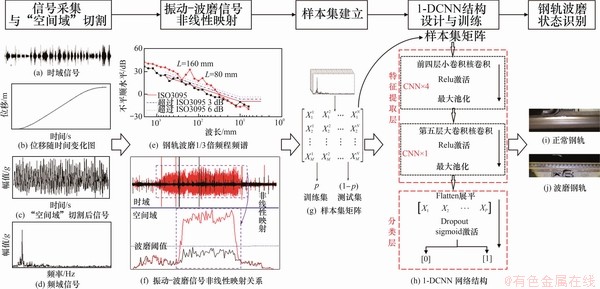
图1　基于1-DCNN的钢轨波磨状态识别流程

Fig. 1　Process of rail corrugation identification based on 1-DCNN

2.1　信号采集与“空间域”切割

通过在列车轴箱处安装加速度传感器以获得振动信号，图1(a)所示为采集到的轴箱垂向振动时域信号。不同于其他机械结构信号在一定工作时间段内往往具有固定旋转频率，即速度为定值，轨道车辆在实际运营时速度通常表现为非稳态的特征，大部分时刻速度处于震荡变化中。若仍以常见的固定时间窗口对振动信号进行切片划分，则在此时间窗口内列车经过钢轨的位移大小不一，这会对后续钢轨波磨准确定位带来更大的难度。因此，本文提出将振动时域信号转化到位移空间域再进行分割。

首先，对列车速度进行积分，得到图1(b)所示的位移随时间变化图，将振动时域信号引入位移空间域信号。

其次，设置“空间域”窗口。以长度X在位移空间域上滑动，以便定位时间，即找到长度为1*X，2*X，…，(M-1)*X和S时对应的时间T₁，T₂，…，T_M-1，T_M(其中S为总位移，M=[S/X]，[ ]为向上取整运算符)。

再次，将由“空间域”得到的时间序列节点T₁，T₂，…，T_M-1和T_M作为切割点，对原始时域信号进行分割。图1(c)所示为经“空间域”节点切割后的样本时域信号。

最后，由于列车时速不断变化，切割后的每个时域信号长度参差不齐，甚至相差几个数量级，这会大大降低样本数据质量，不利于深度学习网络模型的训练。与此同时，机械振动时域信号具有的平移特性一直是特征提取与识别分类的难点之一，在声源识别、图像追踪等研究领域，信号具有的平移不变性会导致特征提取与识别分类困难，解决这类问题具有重要意义^[31]。傅里叶变换将时域信号转化到频域后可减小平移带来的影响，是一种简单有效的方法。JING等^[28]对比分析时域、频域与时频组合域3种不同数据类型下的卷积网络表现性能，可知当以频域数据为样本集时能大幅提高测试精度。因此，对分割后的时域信号进行傅里叶变换，统一关注某截止频率N以下的频域信号，得到图1(d)所示的频谱，大大降低了原始时域信号伸缩、平移及扭曲带来的变化，将其作为1-DCNN的样本输入进行训练。

综上可知，该方法自适应性地克服了列车时速不断变化导致样本长度不一致与CNN要求的输入样本平移不变的问题，并且通过设置“空间域”窗口长度可任意调节钢轨波磨状态识别定位的分辨率。

2.2　振动-波磨信号非线性映射

有关轴承与齿轮箱等机械系统的故障诊断研究，学术界已制定了响应的标准参考数据集，如凯斯西储大学(CWRU)公开的轴承振动数据、PHM 2009 challenge提供的齿轮箱数据以及国内面向全球公开发布的滚动轴承加速寿命试验数据^[32]，目前世界上没有任何一种公认的钢轨波磨激励下的标准振动数据集。除此之外，由于钢轨波磨具有波浪形磨损特征，导致传统的通过电火花加工技术引入指定故障缺陷再获取对应振动信号的手段不再适用。因此，钢轨波磨与振动信号之间的映射关系需通过其他途径加以表征，并且1-DCNN作为有监督模型，输入样本必须配对相应的标签类型。探寻振动-波磨信号之间准确的映射关系对 1-DCNN的训练至关重要。

对同一区间位置的钢轨使用CAT^[33]采集钢轨波磨信号，利用加速度传感器采集相应位置处轴箱振动信号，通过数学换算便可得到两者之间的映射关系。图1(f)所示为时域内所得为波磨测试信号，图1(e)所示为波磨的1/3倍频程频谱。对2.1节经“空间域”切割后的振动时域信号进行均方根计算便得到图1(f)所示空间域所示波形，通过设置恰当的波磨阈值便可得到振动-波磨信号非线性映射关系，以区分钢轨波磨状态。

2.3　样本集建立

CNN的样本输入数据本质上是计算机可识别的数字矩阵。针对本文所提出的1-DCNN，样本集为M*N的矩阵，即“空间域”划分后的所有样本频域数据。深度学习中，为验证模型的泛化能力，通常将样本集划分为训练集与测试集，若样本集中p为训练集，则剩余(1-p)为测试集。

2.4　1-DCNN结构设计与训练

本文提出的1-DCNN框架如图1(h)所示。图1(h)中，输入层为样本集矩阵；前4层网络结构相同，经小卷积核卷积后通过ReLU激活函数变为1组特征图，送往最大池化层进行降采样；第五层为大卷积核卷积，旨在使上一层输入特征图自动学习面向诊断的局部特征；将最后一个池化层的所有特征图展平形成全连接层，经抑制过拟合技术Dropout处理后，传递到最后的sigmoid分类层。ZHANG等^[34]通过研究发现当作用于振动时域信号时，第一层大卷积核有益于过滤高频噪声污染从而俘获中低频带相关特征信息。与ZHANG等^[34]研究中第一层大卷积核不同的是，本文1-DCNN模型输入样本为频域数据，若第一层卷积核较大，则会破坏频域中各频带相干关系。前4层小卷积核结构在较少参数下加深网络，同时抑制过拟合。第五层大卷积核增加了卷积核滤波提取的特征表达能力，这在一定程度上约束了网络内部协变量转移，提高了网络的识别精度与泛化能力。

在CNN模型中，选择适宜的模型超参数能确保在较高识别精度前提下兼顾模型训练速度。针对本文构建的1-DCNN模型，使用随机搜索法寻找各超参数最佳设置，最终得到如表1所示的1-DCNN参数配置。图2所示为表1参数配置下1-DCNN模型结构细节，其中，前4层小卷积核大小为3*1，第五层大卷积核大小为64*1，步长均为1*1。5层卷积池化结构中卷积核数目分别为2，2，4，4和8，池化层卷积核大小与步长均为2*1。卷积层使用“same”零补命令，使卷积层输入与输出长度相等。采用“Adam”优化器训练网络，学习率设为0.001，损失函数为“binary_crossentropy”。为避免梯度弥散与梯度爆炸，利用批处理样本进行训练，批大小为128。Dropout与Early Stopping技术可有效地抑制训练过程中过拟合问题。本文Dropout设为0.5，早停机制中patience设为20，即当测试集精度在20轮内不再提高时便停止训练。由于模型具有一维特性，输入层在3个方向上仅有长度分量，宽与深均为1。随着卷积池化的交替进行，特征图长度逐渐减小，深度加深，输入信号的拓扑结构特征被网络逐层挖掘并自我学习。

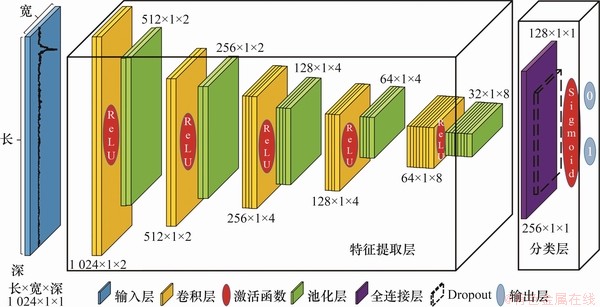
图2　1-DCNN模型结构细节

Fig. 2　Architecture of proposed 1-DCNN model in details

表1　1-DCNN参数配置

Table1　Default settings of 1-DCNN

此外，本文所提出的1-DCNN模型建立在基于Python语言的Keras深度学习库中。PC硬件配置为i7-8700处理器、16 GB内存、Windows 10系统。

2.5　钢轨波磨状态识别

针对钢轨波磨状态识别，定义正常钢轨标签为0，波磨钢轨标签为1。规定若sigmoid激活层输出小于0.5，则判断此样本标签为0，否则为1。通过上述操作，则可以对钢轨波磨状态进行准确识别与定位。

3  试验

3.1　数据说明

对国内某城市地铁线路进行现场试验，如图3所示。使用波磨测试仪CAT测试该线路多个区间的钢轨不平顺，利用B&K3560D多通道数据采集系统获取轴箱振动信号。需要说明的是：试验列车车轮呈初镟状态，使车轮不圆、磨耗及扁疤等引起车辆零部件异常振动的影响源恢复至良好，力求轴箱振动信号主要来自轨道的不平顺激励。

3.2　数据集建立

通过现场试验获得的振动数据经过适当划分便可直接用于1-DCNN的训练。如前文所述，将振动信号进行“空间域”分割，本文设置“空间域”窗口长度X为10 m，将列车经过钢轨每10 m时的时域信号进行切割，再对其进行傅里叶变换，关注截止频率N为1 024 Hz以下的频谱，再将其转化为可供计算机识别的数字矩阵。对现场试验获取的大量振动信号与波磨信号进行统计分析，将波磨阈值设为35(单位为m/s²)，即时域信号均方根值值小于35 m/s²时标签为0，否则为1。从而得到两者之间的非线性映射关系，对样本集数据编辑标签。总之，以“空间域”切割后的时域信号判断样本集的标签类型，其频域信号作为1-DCNN的样本输入。

图3　现场测试图

Fig. 3　Pictures of field tests

以上述方法处理现场试验数据，共得到13 460条样本及其对应的标签，其中90%作为训练集，10%作为测试集，表2所示为钢轨波磨样本集的具体描述。

表2　钢轨波磨样本集描述

Table 2　Descriptions of rail corrugation datasets

3.3　试验结果与讨论

为减少训练过程中的随机误差，在相同参数配置和PC硬件条件下观察1-DCNN模型10次试验的性能，如图4所示，以测试集的识别精度与每条样本测试耗时作为评判标准以验证模型识别精度与时效性。由图4可看出：10次试验下诊断率(即精度)均不低于99%，单个测试样本耗时均少于0.2 ms，值得注意的是，此1-DCNN模型的样本数据均来源于现场实测，充分说明该1-DCNN模型在复杂现场运营条件和列车速度时变工况下能有效、快速且稳定地对钢轨波磨进行智能识别并分类。与此同时，预测钢轨波磨发生位置与现场实际状况较吻合，印证了2.1小节所提“空间域”理论，即不仅可以对钢轨波磨进行智能识别与分类，还可以对线路上钢轨波磨的空间位置准确定位。

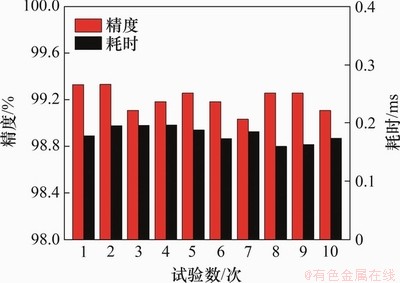
图4　试验结果

Fig. 4　Test results

统计10次试验精度变化范围为99.03%~99.33%，平均精度为99.20%，标准差为0.1；耗时变化仅在1 ms内轻微波动，满足钢轨波磨在线监测时效性需求，因此，本文不再对其进行更深入探究。为进一步了解1-DCNN网络性能，分别以精度最高与最低的第2次、第7次试验为例，分析模型训练过程中其测试精度与标准差曲线演变规律，分别如图5和图6所示。由图5和图6可知：2次试验的精度与标准差在数值上略有差异，并且精度较高的第2次试验标准差较小，但2次试验的曲线总体变化趋势相同；精度与标准差曲线在训练过程中均有所波动，这是1-DCNN模型引入的批处理技术所致。经迭代更新后精度与标准差分别达到本轮训练的最佳值，恰当地批处理样本大小能显著增大计算效率并避免训练误差时而收敛、时而陷入局部最优从而导致诊断精度剧烈波动现象；前5次训练轮数中精度与标准差变化幅度较大，这是由于初始卷积核参数随机设置，经网络的自适应学习后卷积核参数迅速自动调节至一合理区间，后续训练轮数不断缩小此参数区间，精度与标准差随之变化，但其变化速率减小；由于引入Early Sopping机制，在训练轮数达到44次后，精度达到最高不再提高，标准差均收敛到0.06以下。以上现象均符合卷积神经网络训练过程中的自我学习与认知规律，通过分析10次试验下精度最高与最低的试验的精度与标准差曲线变化，更加论证了本文所提1-DCNN方法的鲁棒特性。

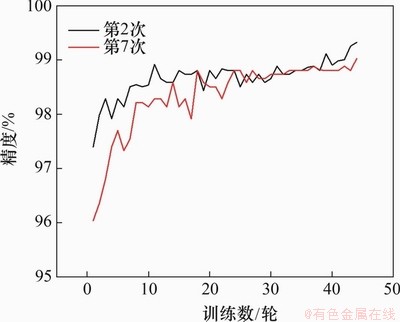
图5　精度演变曲线

Fig. 5　Evolutional curves of accuracy

江航等^[22]在钢轨波磨回归诊断目标输出为(0，1，0)时得到了(0.042 7，0.945 3，0.021 3)的实际输出，朱崇巧^[23]获得了98%的分类识别精度，周志青等^[24]获得了94.67%的识别精度。由上述可知本文提出的基于轴箱振动信号的1-DCNN网络可“端到端”地直接作用于现场实测数据并输出识别结果，识别精度与鲁棒性较高，达到了99.20%，标准差仅为0.1，综合表现性能优于文献[22-24]中的综合性能。以本文数据来源的某城市地铁线路为例，使用波磨测试仪CAT测试该线路每区间的钢轨波磨耗时达1月，而采用本文方法所需总时间不超过3 h，其中包含振动数据的采集与模型的预测，并且可安排正常营运的列车进行在线监测，不影响车辆的日常营运计划。针对亟待解决的钢轨波磨在线监测问题，本文所提出的技术手段能极大地提高生产效率，节省大量人力物力支出，为钢轨波磨在线监测提供新的解决方法。虽然本文提出的方法能准确地识别钢轨波磨在线路上出现的位置，但还不能识别钢轨波磨的波长和波磨的严重程度，这有待于下一步研究。

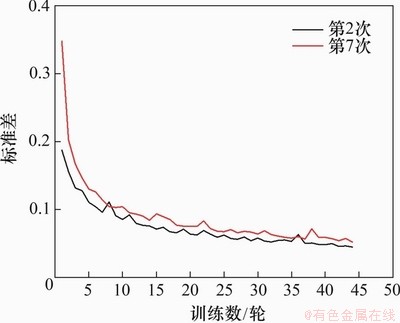
图6　标准差演变曲线

Fig. 6　Evolutional curves of standard deviation

4  结论

1) 构建的前4层小卷积核、第五层大卷积核网络模型可不依赖于人工特征提取与专家经验，直接作用于原始振动频域信号，能“端到端”地对钢轨波磨进行状态识别。

2) 该1-DCNN具有较强的泛化能力和鲁棒特性，即使在复杂的现场运营条件和列车速度时变工况下，仍然保持较高的钢轨波磨识别精度，稳定在99.20%(标准差为0.1)。对每一条样本的识别时间均少于0.2 ms，满足钢轨波磨在线监测的时效性要求。

参考文献：

[1] 李伟. 地铁钢轨波磨成因及其对车辆/轨道行为的影响[D]. 成都: 西南交通大学牵引动力国家重点实验室, 2015: 1-4.

LI Wei. Study on root cause of metro rail corrugation and its influence on behavior of vehicle-track system[D]. Chengdu: Southwest Jiaotong University. State Key Laboratory of Traction Power, 2015: 1-4.

[2] 郭建强, 朱雷威, 刘晓龙, 等. 地铁司机室噪声与钢轨波磨关系的试验与仿真研究[J]. 机械工程学报, 2019, 55(16): 141-147.

GUO Jianqiang, ZHU Leiwei, LIU Xiaolong, et al. Experimental and simulation study on the relationship between interior noise of metro cab and rail corrugation[J]. Journal of Mechanical Engineering, 2019, 55(16): 141-147.

[3] LING Liang, LI Wei, SHANG Hongxia, et al. Experimental and numerical investigation of the effect of rail corrugation on the behaviour of rail fastenings[J]. Vehicle System Dynamics, 2014, 52(9): 1211-1231.

[4] 石怀龙, 王建斌, 戴焕云, 等. 地铁车辆轴箱吊耳断裂机理和试验研究[J]. 机械工程学报, 2019, 55(6): 122-128.

SHI Huailong, WANG Jianbin, DAI Huanyun, et al. Crack mechanism and field test of the metro safety hanger[J]. Journal of Mechanical Engineering, 2019, 55(6): 122-128.

[5] LING Liang, LI Wei, FOO E, et al. Investigation into the vibration of metro bogies induced by rail corrugation[J]. Chinese Journal of Mechanical Engineering, 2017, 30(1): 93-102.

[6] 魏珲, 刘宏立, 马子骥, 等. 基于组合弦测的钢轨波磨广域测量方法[J]. 西北大学学报(自然科学版), 2018, 48(2): 199-208.

WEI Hui, LIU Hongli, MA Ziji, et al. A wide-area measurement method of rail corrugation based on the combination-chord system[J]. Journal of Northwest University(Natural Science Edition), 2018, 48(2): 199-208.

[7] GRASSIE S L. Measurement of railhead longitudinal profiles: a comparison of different techniques[J]. Wear, 1996, 191(1/2): 245-251.

[8] 马子骥, 董艳茹, 刘宏立, 等. 基于多线结构光视觉的钢轨波磨动态测量方法[J]. 仪器仪表学报, 2018, 39(6): 189-197.

MA Ziji, DONG Yanru, LIU Hongli, et al. Rail corrugation dynamic measurement method based on multi-line structured-light vision[J]. Chinese Journal of Scientific Instrument, 2018, 39(6): 189-197.

[9] 罗林, 张格明, 吴旺青, 等. 轮轨系统轨道平顺状态的控制[M]. 北京: 中国铁道出版社, 2006: 115-135.

LUO Lin, ZHANG Geming, WU Wangqing, et al. Control of rail smoothness of wheel/rail system[M]. Beijing: China Railway Publishing House, 2006: 115-135.

[10] HAN Sangbo. Measuring displacement signal with an accelerometer[J]. Journal of Mechanical Science and Technology, 2010, 24(6): 1329-1335.

[11] 徐金辉, 王平, 汪力, 等. 轨道高低不平顺敏感波长的分布特征及其影响因素的研究[J]. 铁道学报, 2015, 37(7): 72-78.

XU Jinhui, WANG Ping, WANG Li, et al. Research on the distribution characteristics and influence factors of sensitive wavelength of track vertical profile irregularity[J]. Journal of the China Railway Society, 2015, 37(7): 72-78.

[12] LI Qingyong, REN Shengwei. A real-time visual inspection system for discrete surface defects of rail heads[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(8): 2189-2199.

[13] WESTEON P F, LING C S, ROBERTS C, et al. Monitoring vertical track irregularity from in-service railway vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2007, 221(4): 75-88.

[14] WESTEON P F, LING C S, GOODMAN C J, et al. Monitoring lateral track irregularity from in-service railway vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2007, 221(4): 89-100.

[15] NAGANUMA Y, KOBAYASHI M, NAKAGAWA M, et al. Condition monitoring of Shinkansen tracks using commercial trains[C]// 2008 4th IET International Conference on Railway Condition Monitoring. Derby, UK: IET, 2008: 18-20.

[16] ALFI S, BRUNI S. Estimation of long wavelength track irregularities from on board measurement[C]// 2008 4 th IET International Conference on Railway Condition Monitoring. Derby, UK: IET, 2008: 1-6.

[17] LEE J S, CHOI S, KIM S S, et al. Estimation of rail irregularity by axle-box accelerometers on a high-speed train[C]// Proceedings of the 10th International Workshop on Railway Noise, Noise and Vibration Mitigation for Rail Transportation Systems. Nagahama, Japan: Springer, 2012, 118: 571-578.

[18] BOCCIOLONE M, CAPRIOLI A, CIGADA A, et al. A measurement system for quick rail inspection and effective track maintenance strategy[J]. Mechanical Systems and Signal Processing, 2007, 21(3): 1242-1254.

[19] MOLODOVA M, LI Zili, DOLLEVOET R. Axle box acceleration: Measurement and simulation for detection of short track defects[J]. Wear, 2011, 271(1/2): 349-356.

[20] SALVADOR P, NARANJO V, INSA R, et al. Axlebox accelerations: Their acquisition and time-frequency characterisation for railway track monitoring purposes[J]. Measurement, 2016, 82: 301-312.

[21] WEI Xiukun, LIU Feng, JIA Limin. Urban rail track condition monitoring based on in-service vehicle acceleration measurements[J]. Measurement, 2016, 80: 217-228.

[22] 江航, 尚春阳, 高瑞鹏. 基于EMD和神经网络的轮轨故障噪声诊断识别方法研究[J]. 振动与冲击, 2014, 33(17): 34-38.

JIANG Hang, SHANG Chunyang, GAO Ruipeng. Wheel/rail fault noise diagnosis method based on EMD and neural network[J]. Journal of Vibration and Shock, 2014, 33(17): 34-38.

[23] 朱崇巧. 基于HHT的高速铁路钢轨波磨检测方法[J]. 电子测量技术, 2018, 41(6): 19-26.

ZHU Chongqiao. Detection method of rail corrugation in high-speed railway based on Hilbert-Huang Transformation[J]. Electronic Measurement Technology, 2018, 41(6): 19-26.

[24] 周志青, 胡茑庆, 黄玉, 等. 基于支持向量机的轨道波磨检测方法研究[C]. 第十三届全国振动理论及应用学术会议论文集, 2019: 193-197.

ZHOU Zhiqing, HU Niaoqing, HUANG Yu, et al. Research on rail corrugation detection method based on support vector[C]// Proceedings of the 13th National Conference on Vibration Theory and Application, 2019: 193-197.

[25] LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444.

[26] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324.

[27] JANSSENS O, SLAVKOVIKJ V, VERVISCH B, et al. Convolutional neural network based fault detection for rotating machinery[J]. Journal of Sound and Vibration, 2016, 377: 331-345.

[28] JING Luyang, ZHAO Ming, LI Pin, et al. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox[J]. Measurement, 2017, 111: 1-10.

[29] LI J, QU W D. Aero-engine sensor fault diagnosis based on convolutional neural network[C]// 2018 37th Chinese Control Conference. Wuhan, China: IEEE, 2018: 6049-6054.

[30] 任浩, 屈剑锋, 柴毅, 等. 深度学习在故障诊断领域中的研究现状与挑战[J]. 控制与决策, 2017, 32(8): 1345-1358.

REN Hao, QU Jianfeng, CHAI Yi, et al. Deep learning for fault diagnosis: The state of the art and challenge[J]. Control and Decision, 2017, 32(8): 1345-1358.

[31] 朱会杰, 王新晴, 芮挺, 等. 基于平移不变CNN的机械故障诊断研究[J]. 振动与冲击, 2019, 38(5): 45-52.

ZHU Huijie, WANG Xinqing, RUI Ting, et al. Machinery fault diagnosis based on shift invariant CNN[J]. Journal of Vibration and Shock, 2019, 38(5): 45-52.

[32] 雷亚国, 韩天宇, 王彪, 等. XJTU-SY滚动轴承加速度寿命试验数据集解读[J]. 机械工程学报, 2019, 55(16): 1-6.

LEI Yaguo, HAN Tianyu, WANG Biao, et al. XJTU-SY rolling element bearing accelerated life test datasets: a Tutorial[J]. Journal of Mechanical Engineering, 2019, 55(16): 1-6.

[33] GRASSIE S L. Short wavelength rail corrugation: field trials and measuring technology[J]. Wear, 1996, 191(1/2): 149-160.

[34] ZHANG WEI, PENG GAOLIANG, LI CHUANHAO, et al. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals[J]. Sensors, 2017, 17(2): 425-445.

(编辑  刘锦伟)

收稿日期： 2020 -06 -01; 修回日期： 2020 -08 -22

基金项目(Foundation item)：四川省科技计划项目(2019YFH0053) (Project(2019YFH0053) supported by the Science and Technology Program of Sichuan Province)

通信作者：温泽峰，博士，研究员，从事轮轨关系及减振降噪研究；E-mail: zfwen@swjtu.edu.cn

引用格式： 谢清林, 陶功权, 温泽峰. 基于一维卷积神经网络的地铁钢轨波磨识别方法[J].中南大学学报(自然科学版), 2021, 52(4): 1371-1379.

Citation: XIE Qinglin, TAO Gongquan, WEN Zefeng. Detection method of metro rail corrugation based on 1-dimensional convolutional neural network[J]. Journal of Central South University(Science and Technology), 2021, 52(4): 1371-1379.