J. Cent. South Univ. Technol. (2008) 15: 95-99
DOI: 10.1007/s11771-008-0019-6
Fatigue properties analysis of cracked
rock based on fracture evolution process
ZHANG Ping(张 平)1, 2, XU Jian-guang(徐建光)3, LI Ning(李 宁)4
(1. College of Civil Engineering, Hunan University, Changsha 410082, China;
2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
3. Northwest Electric Power Test and Research Institute, Xi’an 710054, China;
4. Institute of Geotechnical Engineering, Xi’an University of Technology, Xi’an 710048, China)
Abstract: Fracture evolution process (initiation, propagation and coalescence) of cracked rock was observed and the force- displacement curves of cracked rock were measured under uniaxial cyclic loading. The tested specimens made of sandstone-like modeling material contained three pre-existing intermittent cracks with different geometrical distributions. The experimental results indicate that the fatigue deformation limit corresponding to the maximal cyclic load is equal to that of post-peak locus of static complete force-displacement curve; the fatigue deformation process can be divided into three stages: initial deformation, constant deformation rate and accelerative deformation; the time of fracture initiation, propagation and coalescence corresponds to the change of irreversible deformation.
Key words: rock mechanics; fatigue properties; cyclic loading; fracture evolution; fatigue damage
1 Introduction
Blasting is widely used in excavation of rock engineering and usually responsible for the failure of rock mass. For example, in 1991 a large block of rock of about 2 000 m3 slid from a steep rock face at the disused quarry in Shau Kei Wan of Hong Kong. At the time of the incident, blasting had been taking place above the disused quarry for some time in conjunction with the construction of a new housing estate[1]. Moreover, lots of large-scale slopes became slip under continuous blasting in Zhang-Qing freeway[2]. These incidents indicate that the cumulative damage and long-term stability of the cracked rock under blasting are the most important problems in rock mechanics[3-6]. In order to understand them well, the fatigue properties of cracked rock under dynamic cyclic loading should be further studied.
In recent years, aimed at the fatigue deformation and strength properties of the intact rock, block-jointed rock and cracked rock with intermittent cracks, lots of research work has been made[3-12]. HAIMSON and KIM[3], BROWN and HUDSON[4] earlier pointed out that the fatigue failure curve is controlled by complete force-displacement curve under static loading and is equal to that of post-peak corresponding to the maximal cyclic load. Then, GE et al[6-7] proposed that the fatigue damage of intact rock has a threshold value and the fatigue failure is controlled by cumulative deformation. The amplitude and maximum of cyclic load are the most important influence factors on fatigue lifespan of intact rock. Moreover, LI et al[8-9] investigated the fatigue properties of the cracked gypsum and sandstone with intermittent cracks. Their testing results show that the fatigue properties are prone to be influenced by the crack angle and crack density, and more obvious than non-cracked samples. Furthermore, SHAO et al[10] discussed the influential factors on dynamic fatigue properties for rock mass containing intermittent joints under stress wave, e.g. joints angles, stuffing characteristics and lateral pressures.
However, the essence resulting in the fatigue failure is still not given. Actually, the failure of cracked rock under cyclic loading is a dynamic process. In macroscopic scale, it is an irreversible and cumulative deformation process; in microscopic scale it is originated from the fracture initiation, propagation and coalescence[1]. Therefore, it is hard to reveal the damage and evolution law of cracked rock essentially in macroscopic scale. In order to point out the mechanism of fatigue failure and evaluate the long-term stability of rock engineering, the best way is to study the initiation, propagation and coalescence process of cracked rock under cyclic loading.
In order to study this problem deeply, the fracture initiation, propagation and coalescence process under cyclic loading were monitored using digital camera and digital video camera recorder, and the specimens containing three pre-existing intermittent cracks with different geometrical distributions were used. Then, considering the force-displacement curves under uniaxial cyclic loading, the fatigue properties and the essence of irreversible deformation were revealed.
2 Experimental design
In order to ensure the brittle, frictional and dilatant characteristics of the specimen, the model material used for this investigation consisted of barite, uniformly graded sands, gypsum and water. And the mixture ratio of barite to sand to gypsum to water was fixed by mass as 20?40?23?17 after testing several trial mixtures.
The dimensions of the specimens were 120 mm×60 mm×25 mm as illustrated in Fig.1. The cracks were 12 mm in length (2a) and the distance between two cracks was kept constant at 20 mm (2b) (see Fig.1 for the definition of a and b). The crack inclination angle α (α=β1) was 45?, and the rock bridge angle β2 varied from 75? to 105? with 15? increments (see Fig.1 for the definition of α, β1 and β2). Any geometry was described in the form of “crack angles (α)-rock bridge angle (β1)-rock bridge angle (β2)”; for example “45?-45?-90?” corresponded to the specimen with crack angles α of 45?, rock bridge angle β1 of 45? and rock bridge angle β2 of 90?. The details of the tested samples and dimensional analysis could be seen in Ref.[13].
Cyclic loading tests were carried out under control with the compressive load being programmed to vary between two limits as a triangular function of time using a servo controlled MTS Model 810 machine. To avoid bounding and moving of the samples, a 0.5 kN minimum compressive amplitude was kept under unloading (see Fig.2, in which Fmax and Fmin represent the maximum compressive load and the minimum compressive load, respectively). The loading-unloading frequency was 0.02, 0.2 and 1.0 Hz respectively. In order to monitor the process of fracture propagation and coalescence on the specimen’s surface, the loading was stopped as soon as each cycle has finished. Furthermore, a Nikon CoolpixE995 digital camera and a DCR-TRV 740E digital video camera recorder were used to record the crack propagation and coalescence in or after the loading process.
3 Fatigue properties of cracked rock under cyclic loading
3.1 Characteristics of force-displacement curves
Representative result of 45?-45?-90? cracked sample under cyclic loading is shown in Fig.3. The loading frequency is 1 Hz, and the upper limit force level is 81.6% (the ratio of maximum compressive stress to uniaxial compressive strength). It can be seen from Fig.3 that the hysteresis curve is loose at the beginning of the cycle, and then it becomes tight with the cycles increase. Finally, the hysteresis curve becomes loose again near failure. It develops with loose-tight-loose stages. Moreover, the fatigue deformation limit corresponding to the maximal cyclic load is equal to that of post-peak locus of static complete force-displacement curve.
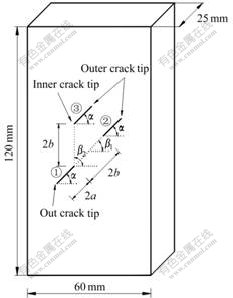
Fig.1 Geometry of model specimen containing three cracks

Fig.2 Wave shape of cyclic loading
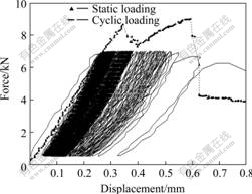
Fig.3 Force-displacement curves of cracked samples under cyclic and static loading
3.2 Evolution law of irreversible deformation
The elastic deformation of the sample releases when unloading, but the irreversible deformation keeps after cyclic loading. Because the irreversible deformation is the essential cause of the fatigue damage, the magnitude and increasing trend of the irreversible deformation can influence the fatigue cumulative damage. Moreover, it is the essential indication of the mechanical performance degradation.
Fig.4 shows the relationship curve of irreversible deformation vs cyclic number (e.g. 45?-45?-90? cracked sample). It can be found from the figure that the fatigue deformation evolution process can be divided into three stages. In the first stage, the irreversible deformation develops very fast; then the deformation becomes stable, and increases with the constant rate in the second stage; finally the cumulative deformation begins to grow noticeably until failure. Obviously, deformation development under cyclic loading is similar to the creep test. So, the axial irreversible deformation can be divided into three stages: initial deformation, constant deformation rate and accelerative deformation using the creep concept[2, 4].
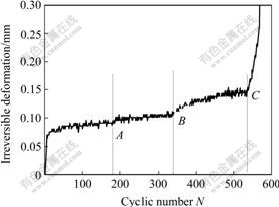
Fig.4 Irreversible deformation vs cyclic number
4 Fracture evolution process
Combining the time record of digital camera and data collecting system of computer, the fracture evolution process (initiation, propagation and coalescence) can be seen at different deformation stages clearly. Fig.5 is the schematic diagram of fracture evolution process of 45?-45?-90? cracked sample under cyclic loading. Fig.5(a) is the cracked sample
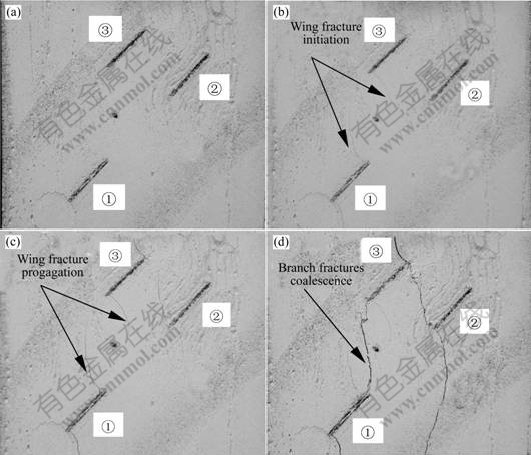
Fig.5 Evolution process of branch fractures under cyclic loading: (a) Pre-cyclic loading; (b) Wing fracture initiation; (c) Wing fracture propagation; (d) Coalescence of branch fractures
without cyclic loading. At this time, there is not any branch fracture on the sample’s surface. When the cycle number reaches 185, the wing fracture appears in the tip of cracks ① and ③ in Fig.5(b). As the cycle number increases, wing fracture begins to propagate along the most compressive stress direction and the branch fracture at the tip of crack ② also appears in Fig.5(c). When the cycle number reaches 586, the tension-shear mixture coalescence happens in the rock bridge of cracks ① and ③. Subsequently, the coalescence also happens in the rock bridge of cracks ② and ③.
Putting the failure process pictures and force-displacement curve together (see Fig.4 and Fig.5), the conclusion can be obtained. Before wing fracture appears first, the irreversible deformation rate increases slowly (see point A in Fig.4). Then, along with the propagation of wing fracture, the increasing amplitude of the irreversible deformation with the cycles grows quickly (see point B in Fig.4). When the branch fractures begin coalescence (see point C in Fig.4), the fatigue deformation (irreversible deformation or total deformation) of cracked sample changes suddenly and the start point of the accelerative stage of irreversible deformation keeps consistent with the time of the coalescence of branch fractures.
As mentioned above, the essence of fatigue failure for cracked sample is the initiation, propagation and coalescence of branch fractures. As the cyclic number increases, the sub-critical stress intensity factor at the tip of pre-existing crack will increase, which will make the branch fracture initiate, propagate and coalesce[14]. And then the deformation including fracture opening, closing and slipping will form. Moreover, the deformation is irreversible. Furthermore, the time of fracture initiation, propagation and coalescence must correspond to the change of irreversible deformation.
That is to say, the development of irreversible deformation can reflect the fracture initiation, propagation and coalescence to some extent. Moreover, the development of irreversible deformation can be regarded as the important parameter of the degree of fatigue damage.
5 Discussion
When the geometrical distributions of cracks in the cracked samples are the same, the coalescence modes of fracture in rock bridge are approximately similar under static and cyclic loading (see Fig.5 and Fig.6). And their deformation at failure (total deformation or irreversible deformation) under different loading conditions is equal (see Fig.3). Namely, the fatigue deformation limit corresponding to the maximal cyclic load is equal to that of post-peak locus of statically complete force- displacement curve.
However, when the geometrical distributions of cracks in the cracked samples are different, the coalescence modes of fracture in rock bridge are different under static or cyclic loading[13]. Certainly, the total deformation or irreversible deformation is different too[15](see Fig.7). All of these indicate that the deformation (total deformation or irreversible deformation) is closely related to the geometrical distribution of cracks and its coalescence mode.
So, although the deformation (especially for the irreversible deformation) can represent the failure process, the influencing factors are very complex, such as the geometrical distribution of cracks and loading condition (uniaxial, biaxial or triaxial loading). That is why it is difficult to establish the complex constitutive relationship or failure criterion in strain space[16-17]. Certainly, if the evolution law of irreversible deformation with loading condition and geometrical distribution of crack can be obtained, the problem will be solved easily.

Fig.6 Failure picture of three-cracked specimen under static loading
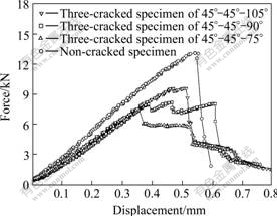
Fig.7 Comparisons of force-displacement curves between non- cracked and three-cracked specimens
6 Conclusions
1) Based on the experimental data on cracked rock-like samples, the fatigue properties are examined under uni-axial cyclic loading. The fatigue deformation process of cracked rock can be divided into initial deformation, constant deformation rate and accelerative deformation. And the fatigue deformation limit corresponding to the maximal cyclic load is equal to that of post-peak locus of static complete force-displacement curve.
2) The time of fracture initiation, propagation and coalescence corresponds to the change of irreversible deformation. So, the mechanism of fatigue damage deformation is due to the fracture initiation, propagation and coalescence.
3) Because the fracture propagation and coalescence are controlled by geometrical distribution of cracks and loading condition, the irreversible deformation in macroscopic scale will also be influenced by these factors. Consequently, the emphasis at next step will be placed on the selection of deformation parameters to establish the damage evolution law in strain space.
Acknowledgements
The authors would like to thank Mr CHANG Xiao-xiao, YANG Shu-guang, XU Bin, QUAN Xiao-juan and LI Guo-yu for their help with the experiments.
References
[1] WONG R H C, CHAU K T. Crack coalescence in a rock-like material containing two cracks[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(2): 147–164.
[2] LI Jian-hua, Zhang Long, Yan Rong-gui. Mechanism of rock slope unstability and critical vibration velocity under action of blasting seismic wave[J]. Mining and Metallurgy, 2001, 10(1): 11–15. (in Chinese)
[3] HAIMSON B C, KIM C M. Mechanical behaviour of rock under cyclic fatigue[C]// CORDING E J. Stability of rock slopes: Proceedings of the 13th Symposium on Rock Mechanics.New York: ASCE, 1972: 845–863.
[4] BROWN E T, HUDSON J A. Fatigue failure characteristics of some models of jointed rock[J]. Earthquake Engineering and Structural Dynamics, 1974, 2: 379–386.
[5] BAGDE M N, PETROS V. Fatigue properties of intact sandstone samples subjected to dynamic uniaxial cyclical loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(2), 237–250.
[6] Ge Xiu-run, Jiang Yu, Lu Yun-de, REN Jian-xi. Testing study on fatigue deformation law of rock under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10): 1581–1585. (in Chinese)
[7] Zhang Qing-xu, Ge Xiu-run, Huang Ming, SUN Hong. Testing study on fatigue deformation law of red-sandstone under triaxial compression with cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 473–478. (in Chinese)
[8] LI N, CHEN W, ZHANG P, SWOBODA G. The mechanical properties and a fatigue-damage model for jointed rock masses subjected to dynamic cyclical loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(7): 1071–1079.
[9] LI N, ZHANG P, CHEN Y S, SWOBODA G. Fatigue properties of cracked, saturated and frozen sandstone samples under cyclic loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(1): 145–150.
[10] Shao Peng, Zhang Yong, He Yong-nian, JIANG Tao. Experimental study on fatigue failure of intermittent jointed rock masses subjected to repeated stress wave[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22): 4180–4184. (in Chinese)
[11] CHEN Feng, MA Chun-de, XU Ji-cheng. Dynamic response and failure behavior of rock under static-dynamic loading[J]. Journal of Central South University of Technology, 2005, 12(3): 354-358.
[12] ZUO Yu-jun, LI Xi-bing, ZHOU Zi-long, MA Chun-de, ZHANG Yi-ping, WANG Wei-hua. Damage and failure rule of rock undergoing uniaxial compressive load dynamic load[J]. Journal of Central South University of Technology, 2005, 12(6): 742-748.
[13] Zhang Ping, Li Ning, He Ruo-lan, XU Jian-guang. Fracture coalescence mechanism of three-intermittent-flaws rock specimen under dynamic loading[J]. Rock and Soil Mechanics, 2006, 27(9): 1457–1464. (in Chinese)
[14] ATKINSON B K. Fracture mechanics of rock[M]. London: Academic Press, 1987.
[15] Zhang Ping, Li Ning, He Ruo-lan, XU Jian-guang. Mechanical properties of fractured media containing intermittent fractures at different strain rates[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 750–755. (in Chinese)
[16] TIEN Y M, LEE D H, JUANG C H. Strain, pore pressure and fatigue characteristics of sandstone under various load conditions[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1990, 27(4): 283–289.
[17] STACEY T R. Simple extension strain criterion for fracture of brittle rock[J]. International Journal of Rock Mechanics and Mining Science and Geomechanics Abstracts, 1981, 18(6): 469–474. (in Chinese)
(Edited by YANG Hua)
Foundation item: Projects(50479023, 50708034) supported by the National Natural Science Foundation of China; Project(20070532069) supported by Specialized Research Fund for the Doctoral Program of Higher Education; Project (20060400263) supported by China Postdoctoral Science Foundation; Project(2007RS4031) supported by Provincial Science and Technology Plan of Hunan
Received date: 2007-06-02; Accepted date: 2007-09-18
Corresponding author: ZHANG Ping, PhD; Tel: +86-731-6710353; E-mail: zp_75@163.com