Composite terminal sliding mode control for class of high-order nonlinear dynamic system

LI Wei (李玮)¹, DUAN Jian-min(段建民) ¹, GONG Jian-wei(龚建伟) ²

 (1. College of Electronic Information and Control Engineering,

Beijing University of Technology, Beijing 100124, China;

2. Intelligent Vehicle Research Center, Beijing Institute of Technology, Beijing 100081, China)

Abstract: A composite control method is proposed based on adaptive terminal sliding mode control and disturbance observer theory for a class of high-order nonlinear dynamic systems. In this control method, the disturbance observer is introduced to estimate system disturbance and the estimated value is used to compensate sliding mode controller’s outputs to restrain the unknown uncertainty. For controller output chattering case, an adaptive law based on disturbance observer is designed. Under the adaptive law, the controller's switching gain can be adjusted automatically, which can reduce the high frequency chattering of outputs. The Lyapunov theory is applied to prove the stability of the control method. Finally, the simulation results of an example show the feasibility and effectiveness of the proposed approach.

Key words: sliding mode control; nonlinear systems; disturbance observer; composite control; Lyapunov methods

CLC number: TG111.3             Document code: A            Article ID: 1672-7207(2011)S1-0267-05

1 Introduction

Recently, the nonlinear dynamic systems which subject to internal parameter variations and external disturbances have received considerable attention. Sliding mode control (SMC) are well known for its excellent robustness to external disturbance and parameter variations, and it is recognized as an effective control method to solve the above problems^[1-16]. The principle of sliding mode control is to make system reach and maintain in the sliding surface or its small neighborhood by discontinuous high frequency switching control, through vary the controller's structure to achieve good dynamic performance. In the sliding mode, the controller is robustness to certain internal parameter variations and external disturbances. In general, the most commonly used sliding surface is the linear sliding surface which can guarantee the tracking error asymptotically stable to equilibrium point. In order to obtain better control performance, the terminal sliding mode control (TSM) with nonlinear sliding surface is recently proposed based on the concept of a terminal attractor^[1]. Compared to conventional sliding mode control, terminal sliding mode control can make system state convergence to equilibrium point in finite time^[2]. To avoid singular points problem^[1], especially existing in MIMO systems, PARK et al^[3] proposed a new terminal sliding surface. This method used compensation function to eliminate the arrival phase of the sliding mode. There is a disadvantage of this approach that it can not be extended to the higher than second-order systems. HU et al^[4] proposed another terminal sliding surface which can extend to high-order nonlinear systems, in addition, this sliding surface overcome the drawback that the derivative of sliding surface is discontinuous.

In order to improve control performance of anti-interference the disturbance-observer based on control (DOBC) theories has been developed in the late of 1980s and have been successfully applied in many fields. In this paper, inspired by HU et al^[4] and DOBC theory^[5-6], a novel composite control method for high-order nonlinear dynamic systems is proposed. The new control method combines disturbance observer and terminal sliding mode control theory. In this method, the disturbance observer is introduced to estimate the system uncertainty, and the estimated value is used to compensate the TSM controller’s outputs which improve the performance and robustness of the controller. In addition, designed adaptive laws based on disturbance observer’s estimated value, under the adaptive law, the controller's switching gain can be adjusted automatically, which could weaken controller's output chattering, overcome the limitation that prior knowledge of the upper bound of uncertainties must be available in conventional TSM control method, and prove the stability of this new control method by Lyapunov theory. Finally, the simulation results of an example are investigated to show the feasibility and effectiveness of this proposed approach.

2 Problem formulation

Consider the following n order MIMO nonlinear dynamic system with state disturbance:

=A₀x(t)+F₀f₀(x,t)+B₀u(t)+d₀(t)    (1)

where x(t)∈Rⁿ is the system state; u∈R^m is the control input matrix; A₀∈R^n×n, B₀∈R^n×m and F₀ are system matrices, rank(B₀)=m; f₀ is nonlinear function which satisfy the bounded conditions described as   assumption 1.

Assumption 1 For any x(t)∈Rⁿ, nonlinear function f₀(x, t) satisfy:

f₀(0, t)=0;‖f₀(x₁, t)- f₀(x₂, t)‖≤‖U₀(x₂-x₂)‖ (2)

External disturbance d₀(t)∈R^m can be formulated by the following exogenous system:

= W w(t);  d₀(t)= Vw(t)         (3)

where U₀, W and V are weighting matrices.

Design the composite controller in next section based on nonlinear dynamic model (1) and external disturbance model (3).

3 Composite controller

Before design the composite controller, the following assumption is given:

Assumption 2 (A_0, B₀) is controllable, (W_, B₀V) is observable, f₀(x, t) satisfy is assumption 1 and the form of f₀ is known, the full state of x(t) is supposed to be available.

3.1 Disturbance observer

The disturbance observer has the form as follows:

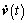=(W+ LB₀V)[v(t)-Lx]+L[A₀ x+ B₀u+ F₀ f₀(x, t)]

=V[v(t)-Lx]             (4)

where is the estimation of w(t),  is the estimation of d₀(t), v(t) is the auxiliary vector of the disturbance observer. The estimation error is denoted as e_w(t)= w(t)-. Based on Eqns. (1), (3) and (6) that the estimation errors e_w(t) satisfy:

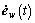=(W+LB₀V)e_w(t)         (5)

Based on regional pole placement and  theory, the following theorem can be obtained ^[7].

Theorem 1 For parameters θ_i＞0, i=1, 2, …, n; supposed existing Lyapunov matrix P＞0 and matrix T satisfy:

＜0

PW+W^TP+TB₀V+V^TB₀^TT^T+Pθ＜0   (6)

where γ=PW+W^TP+TB₀V+V^TB₀^TT^T+I, then by selecting L=P^-1T and θ=diag(θ_i), the estimate error e_w(t) is asymptotically stable^[5-6].

3.2 Terminal sliding model controller

In order to facilitate design of the composite controller, we defined the state vector x in Eqn.1 as following form

x=[x₁, x₂, …, x_n]^T            (7)

Define x₂=,…, x_n=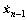, then x(t) can be modified as

   (8)

where f∈R^m is state matrix, b∈R^m×m is input matrix and rank(b)=m, Δf represents the system uncertainty, d(t) denotes the external disturbance. It is easily to see that Eqn.8 is the special case of Eqn.1.

Considering the tracking problems, system states x=[x₁, x₂ , …, x_n]^T, desired states x_d=[x_1d, x_2d , …, x_nd]^T, the error vector is defined as

E= x-x_d =[e, , … , ]^T        (9)

where e= x₁-x_1d, the sliding surface^[4] is

σ(x, t)=CE-W(t)             (10)

where C=[C₁, C₂, …, C_n] and C_i=diag(c_i1, c_i2 ,…, c_im), c_ij(i=1, 2 ,…, n; j=1, 2 ,…, m) are positive constants. W(t)=CP(t),  P(t)=[p(t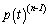)^T, ^T ,…, ^T]^T.

Assumption 3 p_i(t): R₊→R, p_i(t)∈Cⁿ [0, ∞), , …, 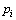⁽ⁿ⁾∈L^∞, the p_i(t) is a bounded interval [0, T] for some T＞0 and p_i(0)=e_i(0), , …, p_i⁽ⁿ⁾ (0) =e_i⁽ⁿ⁾ (0), where Cⁿ [0, ∞) represents the set of all n order differentiable continuous functions defined on [0, ∞).

The function p_i(t) is defined as

  (11)

where the parameters  can be obtained from assumption 3.

By assumption 3 and Eqn.10 we knew that σ(x, 0)=0, it is mean that system’s initial state has been in the sliding mode surface, which guarantees the robustness of the new control method.

3.3 Composite controller

Combined the terminal sliding mode control and DOBC theory to design the composite controller, the structure of the controller is formulated as

u=-+u_TSM               (13)

where u_TSM is the output of terminal sliding mode controller, substituting Eqn.(13) into Eqn.(8), we have

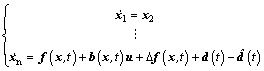 (14)

where  is the estimation of the system disturbance .

Using estimated value from disturbance observer to compensate the controller output. This means that the estimation  can offset the impact of disturbance to some extent. We assume that

‖Δf (x, t)+d(t)-‖≤r₀+r₁‖‖  (15)

where r₀, r₁≥0 are positive constants, r₁∈[0, 1).

Now, design the adaptive laws of the parameters r₀ and r₁.

         (16)

where ,  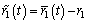are parameter adaptation errors, q₀ and q₁ are positive gains,  and  are the adaptive parameters about r₀ and r₁.

Consider the Lyapunov function as follows:

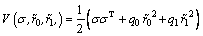     (17)

The time derivation of 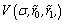 on the terminal sliding mode is

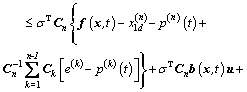
    (18)

Chose the control input u(t) as follows:

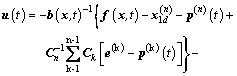
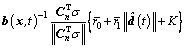   (19)

where K＞0.

Substituting Eqn.(19) into Eqn.(18) yields

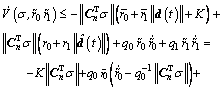
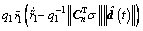          (20)

Substituting the adaptive law (16) into Eqn.(20), it can be obtained that

          (21)

Since K＞0 is positive, the asymptotic stability of the system can be guaranteed.

4 Simulations

To show the robustness of the proposed control method an example was considered. Consider the following system:

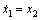
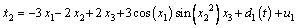
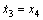
 (22)

where ，，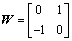  

and the uncertainty is .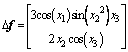

The sliding surface function is 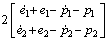, where

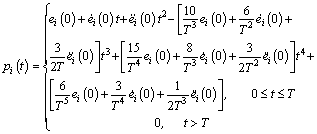
Require the system states to track the expectation states. The system’s expectation states are x_11d= sin(πt/2), x_21d=cos(πt/2). According to section 3, the global terminal sliding mode controller is given as

u=--[u₁ u₂]^T-.

The initial state is x=[2, 0, -1, 0]^T and K=0.25, T=1.5 s.

The simulation results are given in Fig. 1 and Fig. 2 by conventional TSM control strategy and the new control method that proposed in this paper.

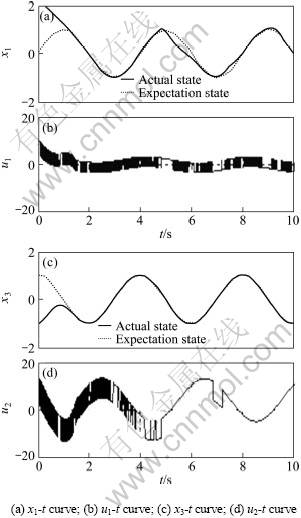
Fig.1 Trajectories by conventional TSM control strategy

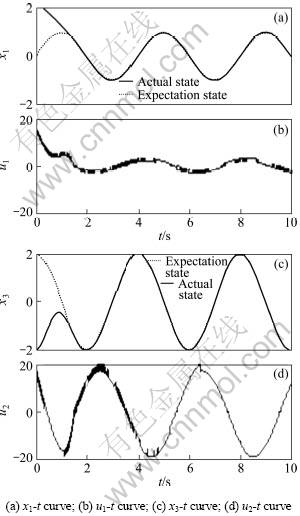
Fig.2 Trajectories by new control strategy

The simulation results by conventional TSM control method are shown in Fig.1 where the dotted lines are the expectation system states. Conventional TSM control algorithm can not make the system states x₁, x₃ tracking the expectation state x_1d, x_3d well and have the controller output chattering problem.

The simulation results by the new control method proposed in this paper are shown in Fig.2 where the dotted lines are the expectation system states. Simulation results show that the control algorithm proposed in this paper can make the system states x₁, x₃ tracking the expectation states x_1d, x_3d well. The tracking error convergence to zero in t=T and reduced the high frequency chattering of control outputs.

5 Conclusions

For a class of high-order nonlinear system, combined with the DOBC theory and adaptive terminal sliding mode control a novel composite control method is proposed in this paper. Firstly, the new control strategy used disturbance observer to estimate system's uncertainty and used the estimate values to compensate controller's output. Secondly, design adaptive laws to achieve sliding mode controller’s switching gain adjustment automatically. Compare to conventional TSM control which fixed the switch gain, the new control method can effectively reduce the controller's output chattering and overcome the drawback that prior knowledge of the upper bound of uncertainties must be available. Prove the stability of this new control method by Lyapunov theory. Finally, a simulation example is presented to verify the validity of the proposed control method.

Reference

[1] Man Z H, Paplinski A P, Wu H R. A robust MIMO terminal sliding mode control scheme for rigid robot manipulators [J]. IEEE Transaction on Automatic Control, 1994, 39: 2464-2469.

[2] Wu Y Q, Yu X, Man Z H. Terminal sliding mode control design for uncertain dynamic system [J]. Systems and Control Letters, 1998, 34(2): 281-287.

[3] Park K B, Tsuiji T. Terminal sliding mode control of second-order nonlinear uncertain systems [J]. International Journal of Robust and Nonlinear Control, 1999, 9 (11): 769-780.

[4] Hu J B, Shi M H, Zhuang K Y, et al. Terminal sliding mode control for a class of nonlinear systems [J]. Control Theory & Applications, 2005, 22(3): 495-498.

[5] Chen W H. Harmonic disturbance observer for nonlinear systems [J]. Transactions of the ASME. Journal of Dynamic Systems, Measurement and Control, 2003, 125(1): 114-117.

[6] Guo L, Chen W H. Disturbance attenuation and rejection for systems with nonlinearity via DOBC approach [J]. Robust Nonlinear Control, 2005, 33(15): 109-125.

[7] Wei X J, Lü S L, Zhang H F, et al. Composite disturbance-observer-based control and terminal sliding mode control for complex models [C]//Proceedings of the 2008 Chinese Control and Decision Conference, Yantai, Shandong, 2008: 4127-4132.

[8] Li T H S, Huang Y C. MIMO adaptive fuzzy terminal sliding-mode controller for robotic manipulators [J]. Information Sciences, 2010, 180(23): 4641-4660.

[9] Roopaei M, Zolghadri J M. Chattering-free fuzzy sliding mode control in MIMO uncertain systems [J]. Nonlinear Analysis, Theory, Methods and Applications, 2009, 71(10): 4430-4437.

[10] Frikha S, Mohamed D, Derbel N. Observer based adaptive neuro-sliding mode control for MIMO nonlinear systems [J]. International Journal of Control, Automation and Systems, 2010, 8(2): 257-265.

[11] Chen W, Saif M. Output feedback controller design for a class of MIMO nonlinear systems using high-order sliding-mode differentiators with application to a laboratory 3-D crane [J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 3985-3997.

[12] Floquet T, Spurgeon S K, Edwards C. An output feedback sliding mode control strategy for MIMO systems of arbitrary relative degree [J]. International Journal of Robust and Nonlinear Control, 2011, 21(2): 119-133.

[13] Jin Y Q, Liu X D, Qiu W, et al. Time-varying sliding mode control for a class of uncertain MIMO nonlinear system subject to control input constraint [J]. Science in China Series F (Information Science), 2010, 53(1): 89-100.

[14] Khan Q, Bhatti A I, Iqbal S, et al. Dynamic integral sliding mode for MIMO uncertain nonlinear systems [J]. International Journal of Control, Automation and Systems, 2011, 9(1): 151-160.

[15] Lin C M, Chen L Y, Chen C H. RCMAC hybrid control for MIMO uncertain nonlinear systems using sliding-mode technology [J]. IEEE Transactions on Neural Networks, 2007, 18(3): 708-720.

[16] Bandyopadhyay B, Thakar V K. Discrete time output feedback sliding mode control for nonlinear MIMO system: A stepper motor case [J]. International Journal of Systems Science, 2008, 39(1): 89-104.

(Edited by CHEN Ai-hua)

Received date: 2011-04-15; Accepted date: 2011-06-15

Foundation item: Project (90920304) supported by the National Natural Science Foundation of China

Corresponding author: LI Wei, PhD; Tel:+86-15101648706；E-mail：liwei727@126.com