高渗压条件下裂隙岩体的劈裂破坏特性
刘涛影1,曹平1,范祥1,赵延林2
(1. 中南大学 资源与安全工程学院,湖南 长沙,410083;
2. 湖南科技大学 能源与安全工程学院,湖南 湘潭,411201)
摘要:基于岩体工程中普遍存在节理裂隙岩体,裂隙岩体在地下工程卸荷扰动后形成复杂应力状态和高水头压力的共同作用下将发生压剪复合破坏或拉剪复合破坏,对裂纹面的应力状态进行分析以判定其破坏模式,并进一步研究岩体裂纹开裂特性及岩桥断裂贯通力学机理,建立相应的临界水压和初裂强度判据。同时,对处于水力劈裂状态的高水头压力隧洞围岩的破坏特性进行模拟。研究结果表明:隧洞在高渗透水压的驱动下周边围岩开始发生水力劈裂,形成拉剪劈裂区;随着内水外渗的发展,随即在拉剪劈裂区外侧形成压剪劈裂带,同时,拉剪区和压剪区继续扩展直至渗流衰减趋于稳定。
关键词:复杂应力;裂隙岩体;高渗压;断裂力学准则;水力劈裂
中图分类号:TU452 文献标志码:A 文章编号:1672-7207(2012)06-2281-05
Splitting failure properties of fractured rock under high water pressure
LIU Tao-ying1, CAO Ping1, FAN Xiang1, ZHAO Yan-lin2
(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. School of Energy and Safty Engineering, University of Science and Technology, Xiangtan 411201, China)
Abstract: Based on the fact that fractured rock mass is prevalent in rock engineering, the fractured rock mass disturbanced in the underground after unloading will be in a complex stress states, which will cause compression failure or tension shear failure under the high water pressure, its failure mode by the stress state of the crack was determined based on the principle of rock fracture mechanics, then the cracking characteristics at the crack tip and the fracture mechanics of rock bridge were studied, and the corresponding value of the critical pressure and the splitting tensile strength values of the crack were determined. The damage characteristics of the surrounding fracturing rock in the high water pressure with simulation was studied. The results show that the tunnel surrounding rock driven by the penetration of high water pressure begins to have hydraulic fracturing, and forms a tensile shear splitting area with the development of water leakage. The compression zone outside of the splitting tensile area is immediately formed, and then the tensile shear zones and compression zone continue to expand until the pressure flow attenuation is stable.
Key words: complex stress; fractured rock; high water pressure; fracture failure criterion; hydraulic fracturing
随着岩石力学工程的发展,涉及高渗压条件的情况越来越多。处于高渗压下的裂隙岩体,其力学行为将发生改变,水压力作用将使裂纹面上的有效应力降低,无渗透水压或低渗透水压时裂纹尖端的应力为压应力,在高渗透水压下可能转化为拉应力。尤其是在岩体开挖扰动后,由于局部岩体被卸除,扰动区的应力处于复杂状态,裂纹面有效应力将影响岩体破坏模式。同时,在高渗压条件下,高水压对裂纹岩体具有劈裂作用[1],在高水头压力作用下,岩体内断续裂隙发生扩展,进而对裂纹尖端应力强度因子产生影响,使岩体损伤劣化产生渐进性破坏。国内外由于岩石渗流而造成的工程失事的实例有很多[2],高渗压下岩石力学研究逐渐成为岩土工程研究的热点问题[3-4]。但目前一般是针对高渗压条件下的渗流场进行研究,而应用断裂损伤相关理论对高渗压下的岩石破坏机理的研究较少,黄润秋等[5]针对深埋隧道的涌水问题,分析了在高压水头作用下裂隙的扩展机理,但仅分析了单一裂隙张拉断裂的情况;李宗利等[6]基于工程近似裂纹失稳准则, 推导了处于压剪应力状态下的拉剪复合断裂和压剪复合断裂两种破坏模式下的临界水压计算公式,但其压剪参数需由试验确定, 因此,该计算公式较复杂。盛金昌等[7]也只研究了水工压力隧洞围岩区各种类型裂纹发生Ⅰ型破坏的应力强度因子的计算方法, 分析了张开型复合裂纹发生水力劈裂的理论判据、有水压力作用的压剪断裂应力强度因子的计算及其断裂判据。为此,本文作者根据岩石断裂力学原理, 研究高渗压作用下复杂应力状态下的岩体裂纹的断裂力学特性, 建立复杂应力条件下裂隙岩体发生水力劈裂作用的临界水头压力及初裂强度判据。同时,将该理论应用到某高压引水隧洞中,研究高渗压下围岩的劈裂破坏特性。
1 高渗压下裂隙岩体破坏特性分析
1.1 断裂破坏模式
在地下工程卸荷扰动后形成的复杂应力状态和高水头压力的共同作用下裂隙岩体的受力状态如图1所示。裂隙岩体受远场地应力σ1和σ3作用,裂纹与垂直方向应力σ1的夹角为ψ,同时,裂纹内作用有孔隙水压力p。假定岩体属于脆弹性,渗透水压力沿裂纹各个方向作用力相等,同时假定裂纹面部分闭合,渗透压o在裂纹面未连通区域不起作用,引入系数β以表征连通面积与总面积之比,因此,渗透压力p的贡献变为βp;同时,由于裂纹面的部分闭合,使应力传递发生变化,故引入传压系数Cn、传剪系数Cv,压剪状态下裂纹面上实际传递的有效法向应力和有效切向应力分别为[8]:
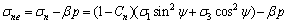 (1a)
(1a)
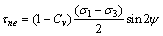 (1b)
(1b)

图1 压剪和拉剪应力状态下裂隙岩体受力示意图
Fig.1 Stress state of the fractured rock mass under condition of compression and tension shear stress
拉剪状态下裂纹面上实际传递的有效法向应力和有效切向应力分别为:
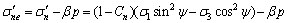 (2a)
(2a)
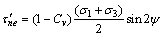 (2b)
(2b)
其中:
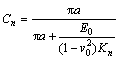 (3a)
(3a)
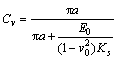 (3b)
(3b)
v0为岩石材料的泊松比;E0为岩石材料的弹性模量;Kn和Ks分别为裂隙的法向和切向刚度;a为裂纹长度。
从式(1b)和(2b)可见:除当ψ=0°或ψ=90°时,裂纹表面的剪应力为0 MPa,裂纹处于纯拉或纯压状态;在其他状态下,裂纹面既有正应力,也有剪应力,因此,裂纹扩展失稳属于I—II复合型,但究竟属于拉剪复合还是压剪复合,则取决于裂纹面法向正应力是拉力还是压力。同时,当ψ=0°或ψ=90°时,裂纹处于纯拉或纯压状态,可以当作特殊状态下的拉复合破坏或压剪复合破坏予以考虑[9]。
1.2 拉剪复合型断裂分析
处于拉剪应力状态的岩体,裂纹表面的法向正应力为拉应力,裂纹的扩展问题属于断裂力学中的I—II拉剪复合型,这时,可得到裂纹尖端应力强度因子 为[10]:
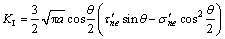 (4)
(4)
将上式对θ求偏导数并令其等于0,即可得到裂纹的开裂角θ0的关系式:
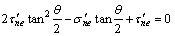 (5)
(5)
将由上式得到的θ0代入式(4),即可得到拉剪应力状态下支裂纹开始起裂时的应力强度因子:
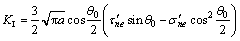 (6)
(6)
在式(6)中,令KI=KIC,得到渗透作用下拉剪岩石裂纹临界水压为:
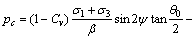
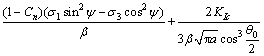 (7)
(7)
进一步可得到渗透作用下拉剪岩石裂纹初裂强度判据为:
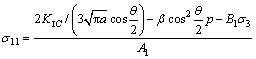 (8)
(8)
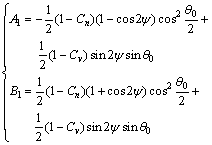 (9)
(9)
此外,还有另外一种拉剪复合破坏,高水头附件一定范围内岩体处于压剪应力状态,但是,在高渗透压力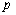 作用下,使得裂纹表面的法向正应力转为拉应力,这时,裂纹的扩展仍属于断裂力学中的I—II拉剪复合型,据式(4),可得到裂纹尖端应力强度因子为:
作用下,使得裂纹表面的法向正应力转为拉应力,这时,裂纹的扩展仍属于断裂力学中的I—II拉剪复合型,据式(4),可得到裂纹尖端应力强度因子为:
 (10)
(10)
将式(10)对θ求偏导数并令其等于0,即可得到裂纹的开裂角θ1的关系式:
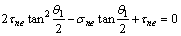 (11)
(11)
将由式(11)得到的θ1代入式(10),即可得到拉剪应力状态下支裂纹开始起裂时的应力强度因子,即
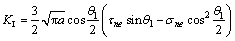 (12)
(12)
在式(12)中,令KI=KIC,得到渗透作用下发生拉剪破坏裂纹的临界水压为:
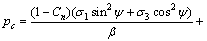
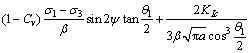 (13)
(13)
进一步可得到压剪应力状态下在高渗压作用发生拉剪破坏的岩石裂纹初裂强度判据为:
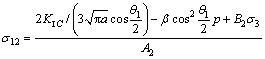 (14)
(14)
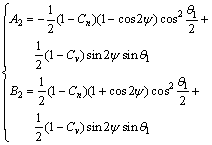 (15)
(15)
拉剪状态下,当KI≥KIC时,翼形裂纹在拉剪应力作用下扩展,扩展中翼形裂纹尖端应力强度因子KI为[11]:
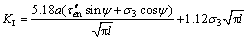 (16)
(16)
其中: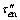 为修正的裂纹面剪切应力τen或
为修正的裂纹面剪切应力τen或  。在式(16)中令KI=KIC,此时裂纹即达到临界值,停止扩展。
。在式(16)中令KI=KIC,此时裂纹即达到临界值,停止扩展。
1.3 压剪复合型断裂分析
当围岩应力较大且渗透压力p较小时,裂纹表面法向正应力为压应力,裂纹的扩展属于I—II压剪复合型,此时剪应力τne迫使裂纹滑移,但同时由于裂纹的部分闭合会产生一个摩擦力μσne+C,剪应力τne要抵抗该摩擦力,这样,裂纹滑移的剪应力τne修正为有效剪切驱动力τeff:
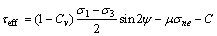 (17)
(17)
其中:μ为裂纹面摩擦因数;C为裂隙面黏结力。
以裂尖为坐标原点的极坐标系中(r,θ)处的σθ可表示为:
 (18)
(18)
由文献[12]可得裂纹尖端应力强度因子为:
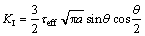 (19)
(19)
根据最大周向正应力理论,初始裂纹沿周向最大正应力方向扩展,因此,开裂角θ3可用下式求得:
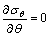 (20)
(20)
由式(18)和(20)可求得θ3=70.5°,将其代入式(19),可得支裂纹起裂时的应力强度因子为:
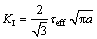 (21)
(21)
在式(20)中令KI=KIC,得到渗透作用下压剪岩石裂纹临界水压为:
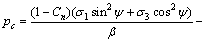
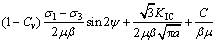 (22)
(22)
同时得到渗透作用下压剪岩石裂纹初裂强度判据为:
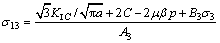 (23)
(23)
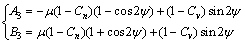 (24)
(24)
在压剪应力状态下,当KI≥KIC时,断续裂纹在有效剪切驱动力τeff作用下滑移形成翼形裂纹,扩展中翼形裂纹尖端应力强度因子KI可采用修正的Kemeny和Cook计算模型。考虑裂纹渗透水压p产生了附加应力强度因子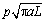 ,此时翼形裂纹尖端应力强度因子为[13] :
,此时翼形裂纹尖端应力强度因子为[13] :

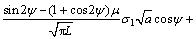
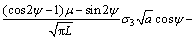
 (25)
(25)
式中:L=l/a,为等效翼形裂纹长度;l为翼形裂纹扩展长度。翼形裂纹沿最大主应力方向扩展直至KI=KIC时裂纹停止扩展。
参考文献[14]的压剪断裂部分试验结果,可绘出压剪复合破坏条件下不同渗透压p与初裂强度关系曲线,见图2。从图2可以看出:岩石裂纹的初裂强度与渗透压呈线性关系;随着渗透压的增加,初裂强度线性减小。这是由于裂纹内渗透压使裂纹表面正应力减小,同时增大了裂纹面的有效剪切驱动力。同理,若渗透压减小,则岩体的初裂强度越大,越不容易破坏。
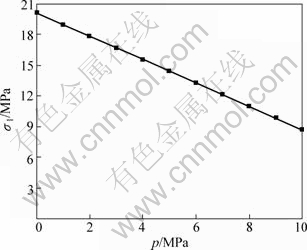
图2 不同渗透压p与初裂强度σ1关系曲线
Fig.2 Splitting strength σ1 under different osmotic pressures p
2 多裂纹岩体破坏特性分析
在实际工程中,岩体裂纹一般不单独存在,对于多裂纹岩体,假定翼形裂纹扩展方向为最大压应力方向,在裂纹扩展初期或裂纹间距较大时,翼形裂纹尖端应力强度因子主要由上述公式控制。但当裂纹的间距较小或随着裂纹扩展时,裂纹间的相互作用会导致裂纹间岩桥的损伤贯通失稳破坏[15],大量实验研究表明裂纹扩展主要有2种形式:(1) 分支翼裂纹扩展相互贯通造成;(2) 裂隙间的岩桥无法抵抗分支裂纹裂尖之间的剪切力而导致裂隙岩体的拉剪复合破坏。本文采用这2种不同破坏模型探讨其在渗透压作用下的断裂贯通力学机理。
2.1 翼裂纹轴向贯通破坏
分支裂纹稳定或不稳定扩展,并最终沿轴向形成贯通的张拉裂纹,造成不同行间裂纹的连通而破坏,见图3。图中,2a为多裂纹长度,D为垂直裂纹方向距离;h为多裂纹介面距离。
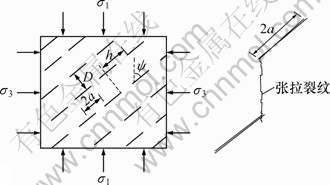
图3 多裂纹分布及翼裂纹轴向贯通示意图
Fig.3 Distribution of multiple cracks and wing crack coalescence
对于此类破坏,当分支裂纹达到临界长度l1c=D/sinψ时,裂纹轴向贯穿。可以此时分支裂纹扩展至临界长度l1c时的裂尖应力强度因子KI作为判据,则有KI=KIC,从而推知其此时的临界水压及初裂强度。
2.2 岩桥拉剪复合贯通破坏
随着分支裂纹的扩展,岩桥间抗剪断能力不断被削弱,当分支裂纹扩展到一定程度时,相邻分支裂纹尖端之间的岩桥被剪切应力剪断,从而造成剪切方向裂纹汇合贯通,岩体被剪切破坏(见图4)。

图4 岩桥拉剪破坏特征图
Fig.4 Failure characteristic of crag bridge shearing
图4中AB为下裂纹的一半,EF为上裂纹的一半,长度都为a,CD为岩桥,BC和DE为翼形开裂裂纹, σCD和τCD分别为作用于岩桥上的正应力和切应力,BC和ED是由主裂纹AB和EF产生的有效剪切驱动力造成的翼形分支裂纹。
对于图4所示的单元体,由力的平衡有:
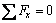 ,
,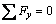 (26)
(26)
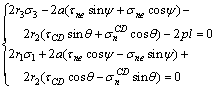 (27)
(27)
式中:
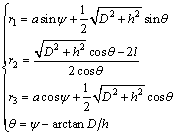 (28)
(28)
从而可得:
 (29)
(29)
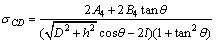 (30)
(30)
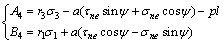 (31)
(31)
假定岩桥剪切破坏符合Mohr-Coulomb强度准则,则破坏条件为
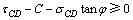 (32)
(32)
将式(29)和(30)代入式(32),整理得:
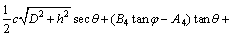
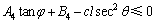 (33)
(33)
联立式(28)和(31),结合前面所得的σen和τen或其修正值,即可得到岩桥发生拉剪复合破坏的临界水压为:
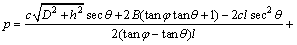
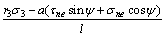 (34)
(34)
同时,可得到岩桥发生拉剪复合破坏的初裂强度判据为:

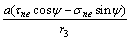 (35)
(35)
以上建立了高渗压条件下裂隙岩体在各种状态下发生劈裂破坏的强度判据。
3 高渗压下围岩破坏数值分析
3.1 数值模型
应用上述理论对某倾斜地下不衬砌压力隧洞破坏特征进行分析[16]。该隧洞围岩裂隙较发育,分布有二组断续裂纹,裂纹分别长2.0 m和1.5 m,且2组节理的裂隙连通率约为60%,内摩擦因素μ=0.3;岩石发生拉剪型破坏裂纹的断裂韧度KIC=15.2 MPa·m1/2,发生压剪型破坏裂纹的断裂韧度KIC=11.2 MPa·m1/2,弹性模量E0=15 GPa,泊松比v0=0.3,耦合计算模型范围见图5。其中:隧洞半径R=4.5 m,地表倾角φ0=40°,内水压力p=6 MPa。岩体屈服准则采用Mohr-Coulomb准则,耦合计算模型力学边界条件:左、右边界及底面均采用法向约束,坡面为自由约束。渗流场边界条件为:隧洞内水压力p=6 MPa,左边界固定水头,坡面水头为0。
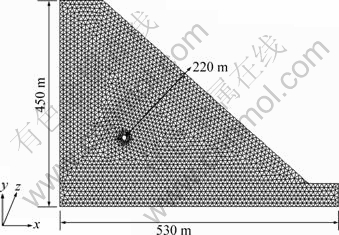
图5 倾斜地表下高渗压隧洞耦合计算模型
Fig.5 Computational model of pressure tunnel under inclined ground
3.2 高渗压下围岩破坏特性分析
压力隧道在运行过程中,在水力梯度的驱动下岩体产生水力劈裂,根据前面的数值模拟条件,利用FLAC3D内置的fish语言功能,可生成高渗压下隧洞围岩劈裂过程变化图(见图6)。
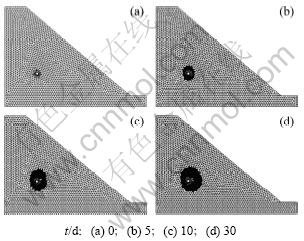
图6 高渗压下隧洞围岩劈裂过程变化图
Fig.6 Process variations of splitting areas surrounding pressure tunnel under high water pressure
从图6可以看出:隧洞充水前只在紧靠洞周的几个单元由于卸荷扰动发生压剪或拉剪起裂,围岩相对完整。充水后高压水直接进入岩体裂隙中,周边围岩在高渗透水压的驱动下超过临界水压力开始发生水力劈裂,而裂隙围岩体在地下工程卸荷扰动后形成复杂应力状态,围岩周边可能处于压剪应力状态和拉剪应力状态,但此时在高水头压力下都将发生拉剪复合破坏,从而在围岩周边形成拉剪劈裂区,随着内水外渗的发展,裂隙贯通区又会引起新的水力劈裂区的扩展。随着围岩加深及渗透压力的减小在拉剪劈裂区外侧形成压剪劈裂带,同时拉剪区和压剪区继续扩展直至渗流衰减至低于临界力而趋于稳定。随着渗流的发展,劈裂带更趋向坡体方向扩展,岩体深部的劈裂扩展受到制约。这是因为往坡体方向岩体的主应力越来越小,从而岩体破坏时临界水压力也越小,而深部方向的临界水压力变化规律则相反。数值模拟与前面的理论分析一致。图7所示为监测到的劈裂破坏区体积的变化曲线。
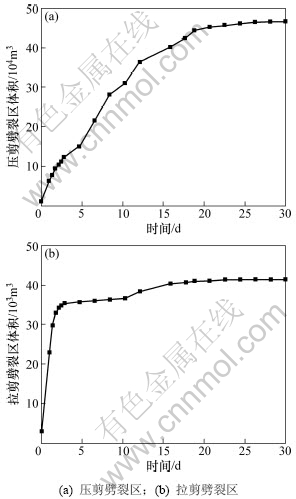
图7 高渗压下隧洞围岩劈裂区变化图
Fig.7 Evolvement of splitting area surrounding pressure tunnel under high water pressure
4 结论
(1) 工程岩体开挖扰动后,由于局部岩体被卸除,扰动区的应力处于拉压复杂应力状态;同时,在高渗压条件下,水压力作用将影响裂纹面上的有效应力,在无渗透水压或低渗透水压为压剪应力状态的岩体,在高渗压下可能转化为拉剪状态。在高水压劈裂作用下,岩体内裂隙发生扩展,对裂纹尖端应力强度因子产生影响,裂隙岩体损伤劣化发生压剪复合破坏或拉剪复合破坏。
(2) 在高渗压作用下,洞周依次形成拉剪劈裂区和压剪劈裂区,且拉剪劈裂区和压剪劈裂区具有不同的扩展演化过程;同时,劈裂区向着主应力减小的方向扩展。理论分析结果与模拟结果一致,该理论可用于研究高渗压下岩石力学工程。
参考文献:
[1] Guo F, Morgenstern N R, Scott J D. Interpretation of hydraulic fracturing breakdown pressure[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(6): 617-626.
[2] 张有天. 岩石水力学与工程[M]. 北京: 中国水利水电出版社, 2005: 6-15.
ZHANG You-tian. Rock hydraulics and engineering[M]. Beijing: China Water Power Press, 2005: 6-15.
[3] 徐德敏. 高渗压下岩石(体)渗透及力学特性试验研究[D]. 成都: 成都理工大学土木工程学院, 2008: 7-16.
XU De-min Permeability and mechanics characteristics test studying on rock or rock mass under high seepage pressure[D]. Chengdu: Chengdu University of Technology. School of Civil Engineering, 2008: 7-16.
[4] Klee G, Rummel F, Williams A. Hydraulic fracturing stress measurement in Hong Kong[J]. International Journal Rock Mechanics Mining Science, 1999, 36: 731.
[5] 黄润秋, 王贤能, 陈龙生. 深埋隧道涌水过程的水力劈裂作用分析[J]. 岩石力学与工程学报, 2000, 19(5): 573-576.
HUANG Run-qiu, WANG Xian-neng, CHEN Long-sheng. Hydro-splitting off analysis on under ground water in deep-lying tunnel and its effect on water gushing out[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(5): 573-576.
[6] 李宗利, 张宏朝, 任青文, 等. 岩石裂纹水力劈裂分析与临界水压计算[J]. 岩土力学, 2005, 26(8): 1216-1220.
LI Zong-li, ZHANG Hong-chao, REN Qing-wen, et al. Analysis of hydraulic fracturing and calculation of critical internal water pressure of rock fracture[J]. Rock and Soil Mechanics, 2005, 26(8): 1216-1220.
[7] 盛金昌, 赵坚, 速宝玉. 高水头作用下水工压力隧洞的水力劈裂分析[J]. 岩石力学与工程学报, 2005, 24(7): 1226-1230.
SHENG Jin-chang, ZHAO Jian, SU Bao-yu. Analysis of hydraulic fracturing in hydraulic tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1226-1230.
[8] 易顺民. 裂隙岩体损伤力学导论[M]. 北京: 科学出版社, 2005: 8-25.
YI Shun-min. Introduction to damage mechanics fractured rock[M]. Chongqing: Science Press, 2005: 8-25.
[9] 李宗利. 岩体水力劈裂机理研究及其在地下洞室围岩稳定分析中的应用[D]. 南京: 河海大学土木工程学院, 2005: 22-25.
LI Zong-li. Study on rock hydraulic fracturing mechanism and application to stability analysis of tunnel surrounding rock[D]. Nanjing: Hohai University. School of Civil Engineering, 2005: 22-25.
[10] Ashby M F, Hallam S D. The failure of brittle solids containing small cracks under compressive stress states[J]. Acta Metall, 1986, 34(3): 497-510.
[11] 郑少河. 裂隙岩体渗流场—损伤场耦合理论研究及应用[D]. 武汉: 中国科学院武汉岩土力学研究所, 2000: 75-82.
ZHENG Shao-he. Research on coupling theory between seepage and damage of fractured rock mass and its application to engineering[D]. Wuhan: Chinese Academy of Scinces. Wuhan Institute of Rock and Soil Mechanics, 2000: 75-82.
[12] Lajtal E Z. Fracture in compression[J]. Int Frac, 1977, 10(4): 12-15.
[13] 赵延林, 曹平, 林杭, 等. 渗透压作用下压剪岩石裂纹流变断裂贯通机制及破坏准则探讨[J]. 岩土工程学报, 2008, 30(4): 511-517.
ZHAO Yan-lin, CAO Ping, LIN Hang, et al. Study on fracture mechanism and rheologic fracture failure criterion of compressive-shear rock cracs under saturated pressure[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(4): 511-517.
[14] 周群力. 岩石压剪判据及其应用[J]. 岩土工程学报, 1987, 9(6): 67-73.
ZHOU Qun-li. Compress shear fracture criterion of rock and it's application[J]. Chinese Journal of Rock Mechanics and Engineering, 1987, 9(6): 63-73.
[15] 郭少华, 孙宗颀, 谢晓晴. 压缩条件下岩石断裂模式与断裂判据的研究[J]. 岩土工程学报, 2002, 24(3): 304-308.
GUO Shao-hua, SUN Zong-qi, XIE Xiao-qing. Research on mode and criterion of rock fracture under compressive loading[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 304-308.
[16] 赵延林. 裂隙岩体渗流—损伤—断裂耦合理论及应用研究[D].长沙: 中南大学资源与安全工程学院, 2009: 148-199.
ZHAO Yan-lin. Coupling theory of seepage-damage-fracture in fracture rock masses and its application[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2009: 148-199.
(编辑 陈灿华)
收稿日期:2011-06-21;修回日期:2011-08-26
基金项目:国家自然科学基金资助项目(10972238);中南大学研究生学位论文创新基金专项科研项目(2010ssxt240);中南大学米塔尔学生创新项目(11MX22)
通信作者:曹平(1959-),男,湖南祁东人,教授,博士生导师,从事岩土工程的教学与科研工作;电话:0731-88879263;E-mail:pcao_csu@sina.com