J. Cent. South Univ. Technol. (2011) 18: 153-158
DOI: 10.1007/s11771-011-0673-y
Lightweight design of 45 000 r/min spindle using full factorial design and extreme vertices design methods
PARK Seong-jin, LEE Choon-man, HWANG Young-kug
Department of Mechanical Design and Manufacturing Engineering, Changwon National University,
Changwon 641-773, Korea
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: Factors for determining the spindle size are the shaft diameter, positions of bearing and motor, and entire length of the spindle. Then, it is important to find the assembling of the optimal design variables, which satisfy the stiffness and rotational speed required to the spindle. A general full factorial design method was used to verify some factors that affect the natural frequency of a spindle. It is verified that the shorter shaft length and bearing span length represent the higher natural frequency, and there are some effects according to the change in the levels of factors. The detailed spindle dimension is determined by applying an EVD method, which can define the optimal bearing position through considering the limiting condition. Based on the estimated regression model, the optimal spindle size and bearing distance that can improve the primary natural frequency are obtained, and the influence of design factors on the natural frequency is also analyzed.
Key words: high-speed spindle; extreme vertices design; natural frequency; lightweight design; full factorial design
1 Introduction
The basic functions required to the spindle system of recent cutting machine tools are high rotational accuracy with low vibration, low temperature increases, high strength with a high damping ratio, and long life. In these functions, the high rotational accuracy with low vibration has been recognized as the most important factor according to the increase in demands for the fields of aircraft parts and semiconductors. In addition, it is necessary to perform a ultra high accuracy process that can achieve nano class precision and a high-speed machining process using an ultra high-speed spindle simultaneously.
A spindle system is configured as a mass-spring system with a spindle and bearings and has a natural frequency. In the case of the number of rotation in a spindle that is lower than the natural frequency, it shows no problems. However, if the number of rotation in a spindle exceeds the natural frequency, it may present a difficulty in a machining process due to the resonance and this leads to the destroy of the spindle. Such a vibration problem directly affects the machining accuracy and may cause some problems in the life of bearings and the safety of tool holders.
In order to solve the vibration problem, it is very important to ensure stable static stiffness. Also, it is very important to determine some factors in bearings, such as bearing stiffness, distance between bearings, spindle size, shape of spindle interface, and bearing contact angle, for guaranteeing the stable static stiffness in a spindle system. In these factors, the spindle size and the distance between bearings are very important factors for determining not only the stiffness of a spindle system but also the speed limit of bearings and the natural frequency of a spindle.
In general, if the concept design of a spindle system in machine tools is implemented and then the configuration is determined, the size of the spindle will be examined. In such a size examination step, the analyses of stiffness and dangerous speed are largely implemented. Then, it is important to find the assembling of the optimal design variables, which satisfy the stiffness and rotational speed required to the spindle. Lots of studies on the optimization of spindle systems have been conducted, and various methods and results have also been presented [1-6]. In recent years, SHIN and LEE [7] planned some experiments using a central composite method and performed the optimization of the position of bearings and spindle diameter through implementing the design optimization using a multiple response optimizing method. HWANG and LEE [8] proposed mixture contour plots and estimation equations that are able to determine the spindle size and the distance between bearings using an extreme vertices design method, which can consider various limiting conditions. In addition, MAEDA et al [9] consider more than two bearings in the spindle model and take into account of the chatter stability that is totally related to the dynamic properties of the spindle.
The objective of this study is to propose two step design method to improve the stiffness and natural frequency of a spindle. Design parameters of the spindle were obtained from a general full factorial design method in the first step. And then, the optimum detailed spindle dimensions based on the bending natural frequency were obtained from an extreme vertices design method that can consider various limiting conditions occurring in the design of the spindle in the second step. In addition, the design was applied to a 45 000 r/min actual product.
2 Analysis model of spindle system
Table 1 lists the specification of the spindle, which is to be developed in this study. The arrangement of bearings was determined by DBB that has been known as a proper way for a high-speed spindle. In the four- column combination, the stiffness of a single bearing was 49 N/μm, and the spindle presented a motor embedded structure.
Table 1 Specifications of spindle

The analysis model was established, which estimated the bending natural frequency using the ARMD, an exclusive analysis program for a rotating body. Fig.1 illustrates this analysis model. The rotor of the motor was determined as a disk, where mass and inertia effects were only considered, and in the bearing the effect of stiffness was considered only.
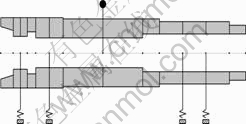
Fig.1 Analysis model of rotor shaft-bearing
3 Concept design using full factorial design method
3.1 Full factorial design
A general full factorial design method is used in all combination figures according to experimental factors and can be used to implement a small scale screening test or optimization test. In the first step, a general full factorial design method was used to verify some factors that affected the natural frequency of a spindle. The entire length of a spindle that could be varied, the distance between the front race and the rear race, and the assembling position of the rotor were determined as such factors, as shown in Fig.2. Table 2 lists these factors and the levels of these factors.

Fig.2 Initial variables for spindle design
Table 2 Design factors and levels of experiments

3.2 Analysis of full factorial design
In the computational experiment, a total of 27 analyses for the full factorial design were implemented. Fig.3 shows the major effects of this experiment. It was verified that the shorter shaft length and bearing span length represented the higher natural frequency, and there were some effects according to the change in the levels of factors. However, in the case of the rotor position, it could be seen that there were no effects according to the change in the levels of factors because there was no difference in the average value.
From the results of the analysis, the natural frequency increased with the decrease in the spindle length. Thus, it is a better way to configure as a shorter spindle length as possible for designing a high-speed spindle. However, it is difficult to reduce the spindle length using the existing commercial drawbar. Thus, the drawbar was designed in this study. Whereas, in the case of a clamping system, it is not possible to unlimitedly reduce the drawbar length because there is a proper tension level required according to the specification of
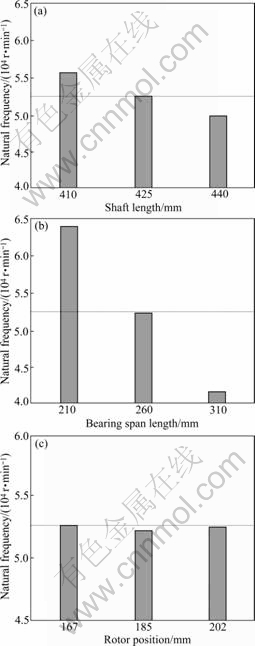
Fig.3 Main factors plot for spindle critical speed: (a) Shaft length; (b) Bearing span length; (c) Rotor position
the spindle interface. Therefore, two drawbars, which are able to put out to an external company, were selected. Because this would be a limiting condition in the spindle design, the detailed spindle dimension will be determined by applying an EVD method, which can define the optimal bearing position through considering the limiting condition.
4 Detail design using extreme vertices design method
4.1 Extreme vertices design
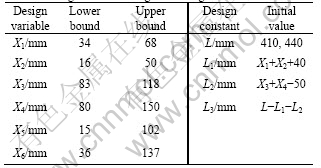
The spindle lengths based on these producible drawbars were 410 and 440 mm. An extreme vertices design method was used to compare the optimal bearing position for these two cases in the second step. For applying the extreme vertices design method, first, the design factors are to be determined. Then, the lower and upper limiting conditions and whole limiting conditions for the determined design factors are to be determined.
Factors for determining the spindle size are the shaft diameter, positions of bearing and motor, and entire length of the spindle. The spindle shaft diameter limited by bearings and motors and the entire shaft length determined by the previous analysis were configured as fixed variables. The distance between bearings and the motor position were determined as design factors.
Fig.4 shows the variables for determining the spindle size and the distance between bearings.

Fig.4 Design variables for bearing and motor locations
In design factors, X1 is the distance between the spindle nose and the primary front race, X2 is the distance between two front bearings, X3 is the distance between the front bearing and the center of the rotor, X4 is the distance between the rotor and the primary rear bearing, X5 is the distance between rear bearings, and X6 is the distance from the secondary rear bearing to the end of the spindle.
In addition, in the stiffness of a spindle system, the determination of the distance between bearings, the selection of bearings, and the determination of the shaft diameter are also important factors. Therefore, although the selection of high stiffness bearings and the decrease in the overhang and the distance between bearings become good ways, it is necessary to carefully determine these factors because excessively small values will badly affect the life of bearing. In general, the recommended values are determined by the following equations [10]:
3d0≤L≤4.5d0 (1)
L/3≤C≤L/2 (2)
where L is the distance between bearing supports, C is the length of the overhang, and d0 is the external diameter of the main shaft. Table 3 shows the range of design factors based on the recommended range presented in Eqs.(1) and (2).
Table 3 Design variables range and design constant
4.2 Analysis of extreme vertices design
Computational experiments were performed for 54 cases using the ARMD for two spindle lengths, 410 mm and 440 mm. Also, the MINITAB was used to analyze the results of these experiments.
A proper model between the component and the response variable is to be estimated after obtaining the data produced through the composite experiment using an extreme vertices design method. The estimated model can be used to find a proper mixing ratio that maximizes or minimizes the response. Mixture regression, stepwise regression, forward selection, and backward elimination methods were used to estimate a proper response surface model [11]. In this study, the analysis was performed using a special third-order model by selecting the mixture regression method in order to configure the spindle size obtained by applying the extreme vertices design method.
In the results, in the case of the p-value that is determined by 0 for the special third-order model, the determination coefficients  for the shaft lengths of 410 mm and 440 mm were 97.82% and 97.53%, respectively. Thus, the estimated special third-order model was suitable.
for the shaft lengths of 410 mm and 440 mm were 97.82% and 97.53%, respectively. Thus, the estimated special third-order model was suitable.
Based on the estimated regression model, the optimal spindle size and bearing distance were obtained, and the influence of design factors on the natural frequency was also analyzed.
Fig.5 shows the response trace plot of the natural frequency. The response trace plot represents the influence of each element at the center point of the experimental region on response values relatively. From the results, the gradients of all design factors showed large values. Thus, all design factors significantly affected the natural frequency. Also, it was possible to verify the types of design factors that can improve the natural frequency and their contribution to the characteristic values according to the change in the ratio.
Fig.6 and Fig.7 represent the contour plots that show how response variables are related to the factors, based on the model equation. In the case of the variable of X1, lots of cases were determined according to the specification and development purpose in the early

Fig.5 Response trace plot of critical speed: (a) Shaft length of 410 mm; (b) Shaft length of 440 mm
design stage. In this case, the installation of a labyrinth seal should be considered. Thus, it was fixed as 60 mm and 50 mm. The variables of X2 and X5 are the distance between bearings and the length of an actual spacer, respectively. These were fixed for this analysis.
It was verified that the range, which satisfied the high natural frequency, was extended with the decrease in the value of X1. In addition, it can be seen that the design range, which satisfied the primary natural frequency more than 60 000 r/min in the 440 mm length spindle, decreased compared with that of the 410 mm spindle length. With the increase in the value of X1 for increasing the natural frequency, the static stiffness decreased due to the increase in the over-hang. Also, as it excessively decreased, some dynamic problems occurred due to the large decrease in the natural frequency. Therefore, a designer should configure a proper design range that satisfies the static stiffness and the dynamic characteristics simultaneously. Here, as shown in Fig.6 and Fig.7, if the contour map obtained by using the extreme vertices design method is used, it is possible to easily configure the combination range of the design factors where the static stiffness and the dynamic characteristics are to be satisfied for the desired condition while the specific variables are fixed using some design limiting conditions. Table 4 shows the optimal design plan of the spindle based on the analysis.
Fig.8 presents the spindle structure and drawbar developed by reflecting the optimal bearing position of the 410 mm-long spindle, which is the optimal design plan.
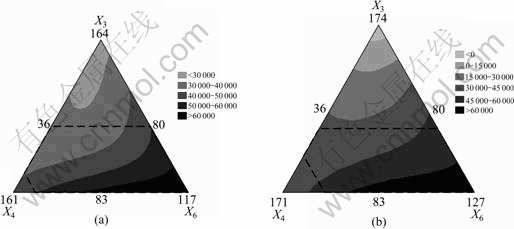
Fig.6 Mixture contour plots according to X3, X4, X6 (spindle length: 410 mm): (a) X1=60 mm, X2=35 mm, X3=35 mm; (b) X1=50 mm, X2=35 mm, X3=35 mm
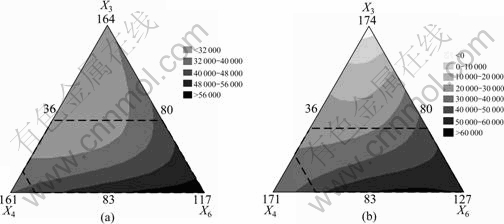
Fig.7 Mixture contour plots according to X3, X4, X6 (spindle length: 440 mm): (a) X1=60 mm, X2=35 mm, X3=35 mm; (b) X1=50 mm, X2=35 mm, X3=35 mm

Fig.8 Schematic drawing of spindle
Table 4 Optimal design plan of spindle

5 Conclusions
1) In the results of the spindle design factors, which affect the natural frequency, using a full factorial design method, there were some effects according to the change in the levels of factors for the bearing distance and spindle length. Thus, the design plan for the spindle shape was configured based on the effects.
2) In the results of the comparison of the natural frequency at the optimal bearing positions for the spindle lengths of 410 and 440 mm, where the producible drawbar length was considered, the short length spindle, 410 mm, showed excellent results in the aspect of vibration design.
3) If the contour plot obtained by the extreme vertices design method was used, it could be expected that it was possible to easily configure the combination range of the design factors where the static stiffness and the dynamic characteristics were to be satisfied for the desired condition while the specific variables were fixed using some design limiting conditions.
Acknowledgement
This work was supported by Grant No. RTI04-01-03 from the Regional Technology Innovation Program of the Ministry of Knowledge Economy (MKE) in Korea.
References
[1] YANG S. A study of the static stiffness of machine tool spindles [J]. International Journal of Machine Tool Design & Research, 1981, 21(1): 23-40.
[2] CHEN W J, RAJAN M, RAJAN S D, NELSON H D. Optimal design of squeeze film dampers for flexible rotor system [J]. Journal of Mechanisms, Transmissions and Automation in Design, 1988, 110(2): 166-174.
[3] RAYLOR S, KHOO B T, WALTON D. Microcomputer optimization of machine tool spindle stiffnesses [J]. International Journal of Machine Tools and Manufacture, 1990, 30(1): 151-159.
[4] NATARAJ C, ASHRAFIUON H. Optimal design of centered squeeze film dampers [J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1993, 115(2): 210-214.
[5] WANG W R, CHANG C N. Dynamic analysis and design of a machine tool spindle-bearing system [J]. Journal of Vibration, Acoustics, Transactions of the ASME, 1994, 116(3): 280-285.
[6] LEE D, CHOI D. Reduced weight design of a flexible rotor with ball bearing stiffness characteristics varying with rotational speed and load [J]. Journal of Vibratrion, Acourtics, Transactions of the ASME, 2000, 122(3): 203-208.
[7] SHIN J H, LEE C M. A study on spindle shape design using design of experiments [J]. Journal of Korean Society for Precision Engineering, 2009, 26(4):120-127. (in Korean)
[8] HWANG Y K, LEE C M. A study on the determination of shaft size using the extreme vertices design [J]. Transactions of the Korean Society of Machine Tool Engineering, 2009, 18(2): 214-220. (in Korean)
[9] MAEDA O, CAO Y, ALTINTAS Y. Expert spindle design system [J]. International Journal of Machine Tools and Manufacture, 2005, 45: 537-548.
[10] KIM M. Study of the clearance control for high speed spindle bearing and optimization of spindle cooling system [R]. 2004, M1-0105-00-0049. (in Korean)
[11] LEE S H. Engineering analysis of statistical data using minitab [M]. Eretec Inc, 2008: 779-797.
[12] AL-SHAREEF K, BRANDON J. On the effects of variations in the design parameters on the dynamic performance of machine tool spindle bearing system [J]. International Journal of Machine Tools and Manufacture, 1990, 30: 431-445.
[13] ALTINTAS Y, CAO Y. Virtual design and optimization of machine tool spindle [J]. CIRP Annals-Manufacturing Technology, 2005, 54 (1): 379-382.
[14] CAO Y, ALTINTAS Y. Modeling of spindle-bearing and machine tool systems for virtual simulation of milling operations [J]. International Journal of Machine Tools and Manufacture, 2007, 47(9): 1342-1350.
[15] CHIEN C H, JANG J Y. 3-D numerical and experimental analysis of a built-in motorized high-speed spindle with helical water cooling channel [J]. Applied Thermal Engineering, 2008, 28: 2327-2336.
[16] BURAGOHAIN M, MAHANTA C. A novel approach for ANFIS modeling based on full factorial design [J]. Applied Soft Computing, 2008, 8: 609-625.
[17] ABELE E, ALTINTAS Y, BRECHER C, Machine tool spindle units [J]. CIRP Annals—Manufacturing Technology, 2010, 59: 781-802.
[18] MA F X, KIM J H, KIM S B, SEO Y G, CHANG Y K, HONG S K, KIM C J. Medium optimization for enhanced production of Rifamycin B by Amycolatopsis mediterranei S699: Combining a full factorial design and a statistical approach [J]. Process Biochemistry, 2008, 43: 954-960.
[19] LIN C W, TU J F. Model-based design of motorized spindle systems to improve dynamic performance at high speeds [J]. Journal of Manufacturing Processes, 2007, 9(2): 94-108.
[20] BEDIAGA I, MUNOA J, HERNANDEZ J, LOPEZ L N. An automatic spindle speed selection strategy to obtain stability in high-speed milling [J]. International Journal of Machine Tools & Manufacture, 2009, 49: 384-394.
(Edited by YANG Bing)
Foundation item: Project(RTI04-01-03) supported by the Regional Technology Innovation Program of the Ministry of Knowledge Economy (MKE) of Korea
Received date: 2010-03-28; Accepted date: 2010-06-24
Corresponding author: LEE Choon-man, PhD, Professor; Tel: +82-55-213-3622; E-mail: cmlee@changwon.ac.kr