Trans. Nonferrous Met. Soc. China 29(2019) 349-357

Self-organized layered growth phenomena of diffusion couples with spinodal decomposition in binary alloys

Yong LU^1,2, Yuan-yuan CUI¹, Qiao-qiao TANG¹, Cui-ping WANG^1,2, Zhen-bang WEI¹, Shui-yuan YANG^1,2, Xing-jun LIU^1,2

1. College of Materials, Xiamen University, Xiamen 361005, China;

2. Fujian Key Laboratory of Materials Genome, Xiamen University, Xiamen 361005, China

Received 21 March 2018; accepted 23 August 2018

Abstract: In order to investigate the formation mechanisms of the layered growth phenomena in diffusion couples with spinodal decomposition, a phase field model combined with elastic strain field was employed. Microstructure evolutions of diffusion couple with spinodal decomposition in binary alloys were numerically simulated by considering concentration fluctuation and elastic anisotropy. The simulation results indicate that the number of the periodical layers decreases with the increase of initial concentration fluctuation, even with large elastic anisotropy. The growth of layered microstructures can be attributed to the directional diffusion enhanced by initially discontinuous chemical potential at the interface.

Key words: spinodal decomposition; concentration fluctuation; phase field method; layered structure; diffusion couple

1 Introduction

The concentration gradient, mismatch degree and microstructure of interfaces have essential effects on the physical properties for various kinds of materials, such as metals [1], semiconductors [2,3] and ceramics [4]. The directionally layered structures formed at the interface are widely reported especially in those materials with spinodal decomposition [5,6]. Due to the fast atom diffusion and defects relaxation at the interfaces, phase separation process near the surface can be strongly influenced [7]. Accordingly, there are several types of microstructures formed at the interface by spinodal decomposition, e.g., spherical, interconnected, layered and mixed [5]. The spherical and interconnected morphologies are the typical spinodal patterns and the layered morphology has been found in binary polymer mixture films accounting for surface-directed spinodal decomposition [8,9]. It is pointed out that the nano-scale layered structure is ultrahard, ultrastable and with high coarsening temperature [10]. Other than that, the electrochemical performance of lithium ion batteries can be enhanced by reasonably designing layer-by-layer structure of electrode [11]. During spinodal decomposition, it is suggested that the concentration fluctuation has significant effects on the mechanisms of phase separation kinetics, even for very superficial quenches [12]. Thus, the transformation progresses of spinodal decomposition triggered by different initial concentration fluctuations at/near the weld interface and internal bulk materials can result in different morphological structures. Therefore, it is necessary to study the effects of concentration fluctuation on microstructure evolutions near the interface of the diffusion couples.

Spinodal decomposition is a process from a uniform, thermodynamic non-equilibrium state to a non-uniform, equilibrium state by aging the system below critical temperature (T_C). The former state is a single phase, while the latter one is composed of two coexisting phases. During annealing, the uniformity could be broken by the growth of concentration fluctuation [5]. The growth dynamics of concentration fluctuation in the early stage of spinodal decomposition in polymer blend [13,14] and alloys [15,16] have been studied by many authors.

However, few researches are focused on the effect of initial concentration fluctuation on spinodal decomposition occurring in binary alloy diffusion couples. The concentration fluctuation is related to the factors such as the temperature, the interactions between elements [17,18]. In diffusion couples, the sharp change of concentration at the weld interface can induce sharp interface of chemical potential and the microstructure near the weld interface may have directional growth tendency [19,20]. In addition, the elastic strain induced by lattice misfit was reported to have considerable effects on the spinodal decomposition [21,22]. Thus, by controlling the process condition (e.g., temperature, composition and interface), layered structures as well as the excellent properties could be acquired.

In this work, we restricted ourselves to simulate the microstructure evolutions in diffusion couples with spinodal decomposition by setting different values of initial concentration fluctuation and composition of the diffusion couples. Considering the elastic misfit strain caused by coherency in the solid alloys, we chose various sets of elastic constants to describe the elastically isotropic and anisotropic systems. Thus, the phase-field method was used to study the morphological evolution in diffusion couples of binary alloy with spinodal decomposition. The microstructure evolutions influenced by the concentration fluctuation with/without the elastic strain field were simulated, where the elastic energy was introduced by combining the microelasticity theory and discrete lattice diffusion equation into the system.

2 Simulation methods

2.1 Phase-field model

2.1.1 Concentration field

Assuming the mobility of species is independent of their positions, the governing equation for a A-B binary alloy can be written by [23]

                     (1)

where c is the molar fraction of species B, F is the total free energy of the system. If the chemical mobility of alloys A and B are assumed to be equal, M is given by [24]

                              (2)

where D is the inter-diffusion coefficient, R is the gas constant and T is the temperature. To further simplify the calculation, the factor c is a constant given by the initial composition, c₀. ξ_c(r, t) is thermal fluctuation at position r and time t in the microstructure which represents concentration fluctuation in this simulation [25]. A Gaussian random noise term satisfying the fluctuation-dissipation theorem, in this case:

     (3)

In this model, the interfacial energy is introduced by gradient term of field variables c and considered isotropic. If the elastic energy is neglected, the total chemical free energy for the A-B binary system is given by

                  (4)

where G(c,T) is the molar Gibbs energy density. In order to study the effect of concentration fluctuations induced by temperature on formation of interfacial layered structure, the following simulations are performed by a constant free energy hump. Thus, the parameters G(c,T) can be expressed as G(c). κ is the gradient energy density. By applying the double-well potential function to the solution phases of the A-B binary system, the molar Gibbs free energy of the system becomes

                  (5)

where c represents the concentration field; ΔG₀ represents the potential barrier;  and  represent the equilibrium compositions.

2.1.2 Elastic energy model

Elastic energy grows out of the lattice mismatch between different phases. The lattice parameters are considered solely related to the composition in the cubic system that is elastically homogeneous. Therefore the intrinsic strain tensor  can be expressed as

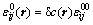                            (6)

where  represents the composition coefficient of crystal lattice parameter and δ_ij is the Kronecker-Delta function. a(c) is the lattice parameter of a solid solution of composition c and a₀ is the lattice parameter of pure solvent. According to the Hooke’s law, the stress σ_ij can be written as a function of elastic strain:

                      (7)

where 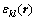 is the total strain measured about a reference lattice, and  is the elastic constant of the cubic system. The factor  is defined to characterize the elastic anisotropy of alloys in cubic crystal structure [26].

Under the above conditions, the elastic strain energy related to the configuration is expressed in the reciprocal space [27]:

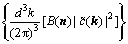                (8)

where  is the Fourier transform of . The integral  in the infinite reciprocal space is evaluated as a principal value excluding a volume 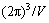 around the point n=0.

             (9)

In the expression, n=k/k represents a unit vector in reciprocal space,  is the Green tensor which is inverse to the tensor .

Thus, the total free energy function of coherent inhomogeneous system can be expressed as

F=F_c+E_el                                                     (10)

3 Simulation results

3.1 Numerical procedures

For numerical convenience, the governing Eq. (1) can be rewritten as the following form:

          (11)

where the dimensionless parameters are given by M′=RTM/D,  F′=F/RT, κ′=κ/RTl², κ′=0.5 with l being the length scale, ,  where l=1.0 represents the dimensionless grid size, (x, y) is the coordinate in the two-dimensional simulation plane, Δt is the dimensionless time, and is a 2-D vector with each component being an independent Gaussian random number of 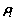. A 2-D simulation region ( 256×64 for free-elastic system and 512×64 for elastic system ) was chosen and averaged into two parts in the x-direction ( the direction perpendicular to the weld interface ). The potential barrier (ΔG₀) is assumed to be RT and the equilibrium compositions (ceq 1 and ceq 2) are 0.1 and 0.9, respectively. The simulation started in the several diffusion couples e.g. AB10/AB50 (which means c_B=0.1 at the left side of the diffusion couple, while c_B=0.5 at the right side of the diffusion couple), AB40/AB60, while the serials of concentration fluctuation =10^-2, 10^-3, 10^-4, 10^-5 and 10^-6 for the system where elastic anisotropy factor (ζ=-1, 0 and 1 ) for elastic system. In the numerical calculation, the dimensionless time Δt=0.001 and the max count of time step is 2×10⁵, while the simulation results were output at appropriate time step. We use periodic boundary conditions in this simulation and three sets of elastic constants are given by (C₁₁=400, C₁₂=200, C₄₄=100), (C₁₁=350, C₁₂=200, C₄₄=150) and (C₁₁=250, C₁₂=100, C₄₄=50) to acquire the different ζ, for 0, -1 and 1.

3.2 Microstructure evolution in diffusion couples without elastic field

To investigate the influences of the initial concentration fluctuation on the microstructure evolution in diffusion couples without elastic field, the simulations are initiated with the different values of concentration fluctuation, e.g. 10^-2, 10^-3, 10^-4, 10^-5 and 10^-6. The concentration fluctuation on the basis of Gaussian distribution to a given initial composition leads to a spontaneous phase separation. The atomic sizes of A and B atoms in the couple are assumed to be the same, while the elastic stress fields induced by lattice misfit are ignored. Therefore, the spinodal decomposition will be driven by the chemical free energy and the interfacial energy. The simulated microstructure evolutions of the diffusion couples AB10/AB50 and AB40/AB60, initiated with different concentration fluctuations are shown in Figs. 1 and 2. In the figures, dark blue indicates the B-rich phase and dark red indicates the A-rich phase. Because the periodic boundary conditions are used in this work, the interface between the left and right ends of the diffusion couple is equivalent to the interface between the diffusion couples.

Fig.1 Simulated microstructures of diffusion couple AB10/AB50 at t=25 with different initial concentration fluctuations

Fig.2 Simulated microstructures of diffusion couple AB40/ AB60 at t=25 with different initial concentration fluctuations

The simulated microstructures of diffusion couple AB10/AB50 at t=25 with initial concentration fluctuation of 10^-2, 10^-3, 10^-4, 10^-5 and 10^-6 are shown in Figs. 1(a)-(e). Since the composition at the left side of the diffusion couple is the equilibrium composition, according to Eq. (4), no spinodal decomposition occurs. At the right side, it can be obviously seen that the interconnected structures appear in the central part and layered structures prefer to form near the interface. The number of the layers gradually increases with the decrease of concentration fluctuation, ξ′_c. Due to the various values of the initial concentration fluctuation, the stages of the spinodal decomposition in the central part of the right side are different. Figure 2 shows the simulated microstructure evolution of diffusion couple AB40/AB60, where the initial compositions on both sides of the diffusion couples are in the spinodal region. By considering different values of initial concentration fluctuation, one can clearly see that layered structures can form on both sides of the interface and the number of the layers increases with the decrease of the concentration fluctuation. Comparing Fig. 2 with Fig. 1, the spherical and rod structures formed instead of interconnected structures. With the increase of concentration fluctuation, the layered structures are gradually broken and disappear due to the coarsening of the particles, as shown in Figs. 2(a) and (b).

The relationships between the number of layers and the concentration fluctuation in different diffusion couples at t=25 are shown in Fig. 3, where N_L represents the number of layers and t represents the dimensionless time. One can clearly see that N_L decreases with the increase of the concentration fluctuation. The relationship curves for the AB10/AB40 and AB10/AB60 are coincident. The values of N_L of AB10/AB50 diffusion couple are larger than the previously mentioned two diffusion couples except for ξ′_c=10^-4. The N_L of the diffusion couple AB40/AB60 is exactly the summation of the N_L of AB10/AB40 and AB10/AB60, which indicates that the concentration gradient between two sides of diffusion couple has little effect on the value of N_L. The number of layers in the diffusion couple AB10/AB50 has linear relationship with the logarithm of the initial concentration fluctuation, while the values of N_L for other three diffusion couples increase sharply between 10^-4 and 10^-2 of concentration fluctuation. It should be mentioned that, according to the simulation results under long time aging, the number of layers increases first and then decreases to a stable value.

Fig. 3 Variation of number of layers (N_L) with logarithms of initial concentration fluctuations in different diffusion couples at t=25

3.3 Microstructure evolution with elastic strain field

During phase separation, if there is large coherent strain between decomposed phases, the elastic strain field should be considered. The different values of elastic anisotropic factor are set to investigate the influences of elastic anisotropy on microstructure evolution, e.g. ζ=0, -1 and 1. The simulation results for AB10/AB50 and AB40/AB60 with different ζ and ξ′_c are shown in Figs. 4-9. The simulation grid size is 512×64.

As can be seen in Figs. 4(a)-(e), by introducing the elastic strain field with anisotropic factor ζ=0 to the diffusion couple AB10/AB50, the microstructure evolutions are similar with the results shown in Fig. 1, where the value of N_L gradually increases with the decrease of concentration fluctuation in the right side. Comparing Fig. 4 with Fig. 1, the alloy decomposed slower than that of the elastically free system.

Figure 5 shows the simulated microstructure of AB10/AB50 with anisotropic factor ζ=-1. The structures of the interface are similar to the previous simulation results, while the internal structures are orderly arranged. The growth of phases during the spinodal decomposition inclined to be directional compared with Fig. 4. As shown in Figs. 5(a)-(e), the elastic anisotropy affects the distribution and growth orientation of the structure, that is, the structure prefers to grow in parallel or perpendicular to the x direction.

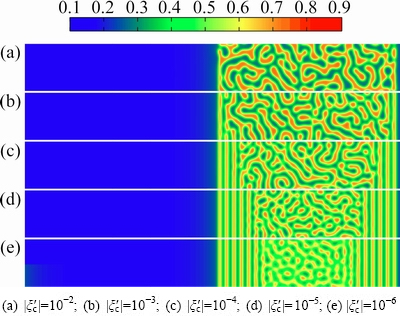
Fig.4 Simulated microstructures of diffusion couple AB10/ AB50 for ζ=0 at t=90 with different initial concentration fluctuations

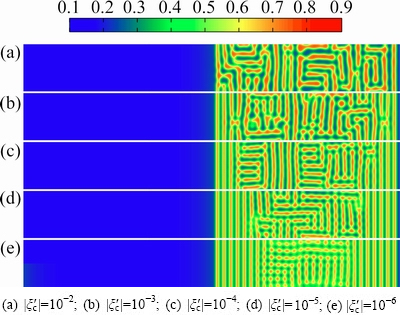
Fig.5 Simulated microstructures of diffusion couple AB10/ AB50 for ζ=-1 at t=70 with different initial concentration fluctuations

Fig.6 Simulated microstructures of diffusion couple AB10/ AB50 for ζ=1 at t=70 with different initial concentration fluctuations

Fig.7 Simulated microstructures of diffusion couple AB40/ AB60 for ζ=0 at t=160 with different initial concentration fluctuations

Fig.8 Simulated microstructures of diffusion couple AB40/ AB60 for ζ=-1 at t=120 with different initial concentration fluctuations

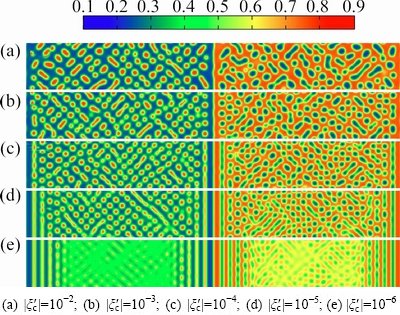
Fig.9 Simulated microstructures of diffusion couple AB40/ AB60 for ζ=1 at t=75 with different initial concentration fluctuations

By given anisotropic factor ζ=1, the simulation results with the same initial composition and the other variable parameters are shown in Fig. 6. Compared with the previous results, lamellar structures are unfavorable to form near the interface of the diffusion couple, due to the growth preferable direction along the 45° or 135° from the x direction. There are no lamellar structures but more obvious interconnected structures formed in  Figs. 6(a) and (b). However, the layered structures still appear in case of small initial concentration fluctuation, as can be seen in Figs. 6(c)-(e).

Figures 7-9 show the simulated microstructure of AB40/AB60 with anisotropic factor ζ=0, -1 and 1. As can be seen, the internal structure tends to be spherical or rod-like. Both sides of the interface form the layered structure and the number of layers are less for ζ=1.

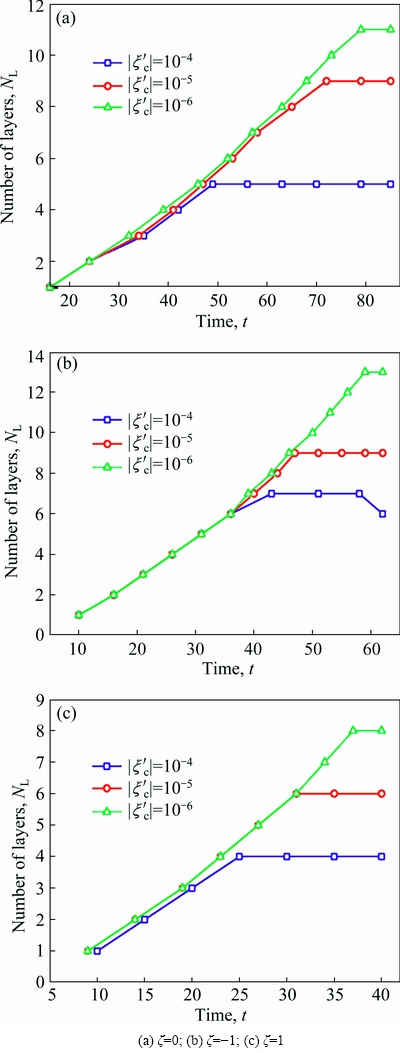
Fig. 10 Variation of number of layers (N_L) with time (t) in diffusion couple AB10/AB50 with different elastic anisotropic factors

The relationships between the number of layers and aging time in the diffusion couple AB10/AB50 for ζ=0, -1 and 1 are shown in Fig. 10. One can see that the number of layers linearly increases with time and reaches a stable value. Figure 11 shows the similar relationship curves of diffusion couple AB40/AB60. The N_L-t curves of the different initial concentration fluctuations were coincident in the early stage. The layers are paired to appear and disappear simultaneously at later stage, so that there are some steps in the curves. The number of layers over time increases at first then decreases as the aging proceeds. The maximum number of layers corresponding to different anisotropic factors in diffusion couples AB10/AB50/ and AB40/AB60 are shown in Table 1.

Fig. 11 Variation of number of layers (N_L) with time (t) in diffusion couple AB40/AB60 with different elastic anisotropic factors

Table 1 Maximum number of layers versus different initial concentration fluctuations ξ′_c for different anisotropic factors ζ in diffusion couples AB10/AB50 and AB40/AB60

4 Discussion

The microstructure evolutions of binary alloy diffusion couples with spinodal decomposition were investigated by considering the effect of initial concentration fluctuation and elastic anisotropy. According to the simulation results, several types of interface microstructures were obtained: spherical, layered, rod-like and interconnected structures. The cross-over morphology of typical spinodal decomposition is the competition of definitive solution of the model equation and inherent concentration fluctuation.

The typical structures of spinodal decomposition, e.g. spherical, rod and interconnected structures are due to the continuous concentration modulation during annealing. However, the progress of the spinodal decomposition process is remarkably affected by the sharp interface between the two diffusion couples. In the diffusion couple AB10/AB50, the B-rich layer forms firstly at the weld interface of the right side that is based on interfacial energy reduction like the surface-directed mechanism [20]. Once the B-rich layer grows near the interface, it is difficult for the A atoms to diffuse through the B-rich layer to the right side, leading to the formation of B-lean layer at the right side of the B-rich layer [28]. Due to the same growth mechanism, the A-rich layer or B-rich layer forms in the new interface constantly, the A-rich and B-rich alternating layers will form. This result is consistent with the reported experimental observations in Fe-Si-Ge diffusion couple, where the self-organized Si-rich and Ge-rich layers formed at the weld interface ascribing to inhomogeneous interdiffusion and spinodal decomposition [6]. However, the spinodal decomposition in the right of diffusion couple continuously proceeds from the beginning. The formation of layered structures near the surface can be interrupted by the normal decomposition far from the interface. In order to apply the present results to real binary alloys, a parameter  can be used to normalize the concentration fluctuation. Accordingly, the lamellar structure could be designed by calculating ξ* with aging temperature and chemical mobility of the alloy. When ξ′_c is large enough, the layered structures will be broken by the local fast spinodal decomposition especially the coarsening stage, while the system with small ξ′_c is preferable to form more layers due to the longer early stage of the decomposition process far from the interface. BALL et al [5] studied the effects of temperature gradients and boundary conditions at the surface of a system separating into two phases via spinodal decomposition, and found that increasing the noise strength the layers formed by slow cooling are roughened. In addition, the volume fraction also has significant effect on the number of layers that smaller volume fraction results in fewer layers by comparing Fig. 1 and 2. In case of smaller fraction of the second phase, the layered structure could form at the early stage and be broken during coarsening [19]. Due to the competing relationship between the directional diffusion at the interface and the typical spinodal decomposition far from the interface, layered structure can only form within a certain range of materials. When the typical spinodal decomposition far away from the interface is developed, only a few layers can form. Therefore, controlling external conditions is of great significance for the formation of layered structure.

According to Figs. 4-9, the elastic anisotropy leads to the obvious difference of microstructure evolution. The evolution of elastic materials decomposed slower than the elastically free system [29]. The slow decomposition kinetics in the diffusion couple with the coherency strain energy are due to the decrease in the driving force of spinodal decomposition as it has been pointed out long time ago by CAHN [30]. The elastically anisotropic materials decompose slightly faster than the isotropic materials because the elastic anisotropy provides soft directions (when ζ<0, the soft direction is <100>; When ζ >0, the soft direction is <111>) that have low strain energy [29]. In the present work, even under elastic strain field, the layered structures still form in case of small initial concentration modulation, which indicated that the chemical potential could dominate the diffusion process. The formation mechanisms are the same as elastic-free system. However, due to the effect of the elastic anisotropy, orientation of the structure for ζ=-1 is parallel/perpendicular to the interface, more layers can form near the interface, and accompanied with the cross-over structure far from the weld interface. In case of ζ=1, the rod-like structures prefer to grow along the direction 45° from the interface, resulting in the discontinuous layered structures near the interface of the diffusion couple. This kind of layered structures can be broken and finally disappear in case of larger difference of phase fractions due to the combined effects of the elastic anisotropy and coarsening.

5 Conclusions

(1) The self-organized periodical layered structure can form near the interface of the diffusion couple during spinodal decomposition. The number of the periodical layers decreases with the increase of initial concentration fluctuation. During long time aging, the number of layers increases first and then decreases to a stable value.

(2) The elastic strain field has remarkable effect on the number of layers near the weld interface and the distribution of internal structures. The layered growth can be enhanced when the preferable growth direction of the spinodal decomposition is parallel to the weld surface.

(3) The growth periodical layered microstructures near the interface of the diffusion couple can be ascribed to the directional diffusion dominated by the discontinuity of the chemical potential at the interface and the following alternate growth of the two phases in spinodal decomposition.

References

[1] HODAJ F, DESRE P J. Effect of a sharp gradient of concentration on nucleation of intermetallics at interfaces between polycrystalline layers [J]. Acta Materialia, 1996, 44: 4485-4490.

[2] ZHANG S, CAO X, WU J, ZHU L W, GU L. Preparation of hierarchical CuO@ TiO₂ nanowire film and its application in photoelectrochemical water splitting [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(8): 2094-2101.

[3] WANG X Q, PEI Y L, MA Y. The effect of microstructure at interface between coating and substrate on damping capacity of coating systems [J]. Applied Surface Science, 2013, 282: 60-66.

[4] SONG S, TAN S, QI X, WANG W, WANG L. Effect of ball peening of substrate on microstructure, phase evolution and properties of electrophoretically deposited YSZ/(Ni, Al) composite coatings [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(11): 2966-2975.

[5] BALL R C, ESSERY R L H. Spinodal decomposition and pattern formation near surfaces [J]. Journal of Physics: Condensed Matter, 1990, 2: 10303.

[6] MATSUKURA B, HIRAIWA Y, NAKAJIMA T, NARUMI K, SAKAI S, SADOH T, MIYAO M, MAEDA Y. Self organization of FeGe/FeSi/FeGe layered structures on Ge and their electrical conduction properties [J]. Physics Procedia, 2012, 23(4): 21-24.

[7] POVSTUGAR I, CHOI P P, TYTKO D, AHN J P, RAABE D. Interface-directed spinodal decomposition in TiAlN/CrN multilayer hard coatings studied by atom probe tomography [J]. Acta Materialia, 2013, 61: 7534-7542.

[8] PURI S, OONO Y. Effect of noise on spinodal decomposition [J]. Journal of Physics A: Mathematical and General, 1988, 21(15): L755.

[9] BASTEA S, PURI S, LEBOWITZ J L. Surface-directed spinodal decomposition in binary fluid mixtures [J]. Physical Review E, 2001, 63(4): 041513.

[10] LIU X C, ZHANG H W, LU K. Strain-induced ultrahard and ultrastable nanolaminated structure in Nickel [J]. Science, 2013, 342: 337-340.

[11] TAN H, HUANG K, BAO Y X, LI Y, ZHONG J X. Rationally designed layer-by-layer structure of Fe₃O₄ nanospheres@ MWCNTs/graphene as electrode for lithium ion batteries with enhanced electrochemical performance [J]. Journal of Alloys and Compounds, 2017, 699: 812-817.

[12] SHIMADA T, DOI M, OKANO K. Concentration fluctuation of stiff polymers III. Spinodal decomposition [J]. The Journal of Chemical Physics, 1988, 88(11): 7181-7186.

[13] XU Y F, HUANG C W, YU W, ZHOU C X. Evolution of concentration fluctuation during phase separation in polymer blends with viscoelastic asymmetry [J]. Polymer, 2015, 67: 101-110.

[14] SATO T, HAN C C. Dynamics of concentration fluctuation in a polymer blend on both sides of the phase boundary [J]. Journal of Chemical Physics, 1988, 88: 2057-2065.

[15] MILLER M K, HYDE J M, HETHERINGTON M G, CEREZO A, SMITH G D W, ELLIOTT C M. Spinodal decomposition in Fe-Cr alloys: Experimental study at the atomic level and comparison with computer models-I. Introduction and methodology [J]. Acta Metallurgica et Materialia, 1995, 43(9): 3385-3401.

[16] MATTERN N, GOERIGK G, VAINIO U, MILLER M K, GEMMING T, ECKERT J. Spinodal decomposition of Ni-Nb-Y metallic glasses [J]. Acta Materialia, 2009, 57(3): 903-908.

[17] HONO K, HIRANO K I. Early stages of decomposition of alloys (spinodal or nucleation) [J]. Phase Transitions: A Multinational Journal, 1987, 10(4): 223-255.

[18] HAFNER J, JANK W. Simple model for the structure and thermodynamics of liquid alloys with strong chemical interactions III: phase separation [J]. Journal of Physics F: Metal Physics, 1988, 18(3): 333.

[19] LU Y, WANG C P, GAO Y P, SHI R P, LIU X J, WANG Y Z. Microstructure map for self-organized phase separation during film deposition [J]. Physical Review Letters, 2012, 109: 086101.

[20] SEOL D J, HU S Y, LI Y L, SHEN J, OH K H, CHEN L Q. Computer simulation of spinodal decomposition in constrained films [J]. Acta Materialia, 2003, 51: 5173-5185.

[21] JOU H J, LEO P H, LOWENGRUB J S. Microstructural evolution in inhomogeneous elastic media [J]. Journal of Computational Physics, 1997, 131(1): 109-148.

[22] LU Y L, CHEN Z, LI Y S, WANG Y X. Microscopic phase-field simulation coupled with elastic strain energy for precipitation process of Ni-Cr-Al alloys with low Al content [J]. Transactions of Nonferrous Metals Society of China, 2007, 17(1): 64-71.

[23] CAHN J W, HILLIARD J E. Spinodal decomposition: A reprise [J]. Acta Metallurgica, 1971, 19(2): 151-161.

[24] HU S Y, CHEN L Q. A phase-field model for evolving microstructures with strong elastic inhomogeneity [J]. Acta Materialia, 2001, 49: 1879-1890.

[25] SHEN C, SIMMONS J P, WANG Y. Effect of elastic interaction on nucleation: II. Implementation of strain energy of nucleus formation in the phase field method [J]. Acta Materialia, 2007, 55: 1457-1466.

[26] OZOLINS V, WOLVERTON C, ZUNGER A. Strain-induced change in the elastically soft direction of epitaxially grown face-centered- cubic metals [J]. Applied Physics Letters, 1998, 72: 427-429.

[27] WEN Y H, SIMMONS J P, SHEN C, WOODWARD C, WANG Y. Phase-field modeling of bimodal particle size distributions during continuous cooling [J]. Acta Materialia, 2003, 51: 1123-1132.

[28] DARUKA I, TERSOFF J. Self-assembled superlattice by spinodal decomposition during growth [J]. Physical Review Letters, 2005, 95: 076102.

[29] CHEN L Q, SHEN J. Applications of semi-implicit Fourier-spectral method to phase field equations [J]. Computer Physics Communications, 1998, 108: 147-158.

[30] CAHN J W. On spinodal decomposition in cubic crystals [J]. Acta Metallurgica, 1962, 10: 179-183.

二元调幅分解型合金扩散偶中自组装片层组织的生长现象

卢 勇^1,2，崔媛媛¹，唐巧巧¹，王翠萍^1,2，魏振帮¹，杨水源^1,2，刘兴军^1,2

1. 厦门大学 材料学院，厦门 361005；

2. 厦门大学 福建省材料基因工程重点实验室，厦门 361005

摘  要：采用耦合弹性场的相场法对调幅分解型合金扩散偶中的片层组织生长现象进行研究，通过考虑浓度起伏和弹性各向异性模拟二元调幅分解型合金扩散偶中的组织演化。模拟结果表明：即使在较大的弹性各向异性条件下，周期性层片组织的层数随着初始浓度起伏的增大而减小。片层组织生长的主要原因可归结于初始界面化学势的不连续所引起的定向扩散。

关键词：调幅分解；浓度起伏；相场法；片层组织；扩散偶

(Edited by Xiang-qun LI)

Foundation item: Project (2017YFB0702401) supported by the National Key R&D Program of China; Project (51301146) supported by the National Natural Science Foundation of China; Projects (20720170038, 20720170048) supported by the Fundamental Research Funds for the Central Universities, China

Corresponding author: Yong LU, Tel: +86-592-2187966, E-mail: luyong@xmu.edu.cn; Xing-jun LIU, E-mail: lxj@xmu.edu.cn

DOI: 10.1016/S1003-6326(19)64944-7