J. Cent. South Univ. (2018) 25: 2399-2409

DOI: https://doi.org/10.1007/s11771-018-3924-3

Effect of bionic mantis shrimp groove volute on vortex pump pressure pulsation

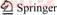
GU Yun-qing(谷云庆)^{1, 2}, ZHANG Wen-qi(张文奇)², MOU Jie-gang(牟介刚)², ZHENG Shui-hua(郑水华)², ZHOU Pei-jian(周佩剑)², FAN Tian-xing(范天星)²

1. School of Energy and Power Engineering, Jiangsu University, Zhenjiang 212013, China;

2. College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: In order to reduce pressure pulsation of vortex pumps, the mantis shrimp was chosen as biological prototype and a bionic engineering model was developed from its abdominal segment grooves. Bionic mantis shrimp groove volute vortex pump models with different numbers of grooves were developed, and numerical simulation methods were used to calculate the models to study the effects of the volute grooves on the pressure pulsation of a vortex pump. The results show that a bionic groove volute could effectively improve the pressure pulsation of a vortex pump outlet, and reduce the pressure pulsation around the pump’s tongue and other internal points. The pressure pulsation under different conditions is impacted by shaft frequency and blade frequency. The bionic groove structure has little effect on the external characteristics of the pump, but could improve the static pressure, velocity distribution, and vortex structure of the flow field. Additionally, pressure pulsation of the whole vortex pump is reduced.

Key words: vortex pump; bionic mantis shrimp groove; volute; pressure pulsation; flow characteristic

Cite this article as: GU Yun-qing, ZHANG Wen-qi, MOU Jie-gang, ZHENG Shui-hua, ZHOU Pei-jian, FAN Tian-xing. Effect of bionic mantis shrimp groove volute on vortex pump pressure pulsation [J]. Journal of Central South University, 2018, 25(10): 2399–2409. DOI: https://doi.org/10.1007/s11771-018-3924-3.

1 Introduction

A vortex pump is a type of rotational-flow centrifugal pump with good anti-clogging performance, widely used in various fields such as agriculture, industry and domestic water. However, the interaction of the rotating impeller and stationary pressurized water chamber results in local cavitation and the formation and collapse of vortices which causes the outlet pressure to pulsate periodically. Three different types of pressure pulsation occur: random pulsation, blade frequency pressure pulsation, and shaft frequency pressure pulsation. These pulsations cause increased vibration of the pump and hydraulic excitation of the internal flow field, impacting efficiency and possibly also leading to further cavitation and vortices. Many scholars have provided research on the pressure pulsation of the pump. MINAKOV et al [1] found that the pressure pulsation of the pump was mainly of the blade frequency type. When the pump was operated below rated conditions, the pulsation amplitude increased significantly, with the maximum amplitude occurring around the tongue. ZHAO et al [2]determined that the distribution of vortices and pressures was closely related to the pressure pulsation in the impeller passages. PEI et al [3] analyzed three-dimensional periodic flow instability of centrifugal pumps under partial load conditions. ZHANG et al [4] found that the sidewall pressurized water chamber could greatly reduce the pressure pulsation of the pump. JIANG et al [5] used the SST k-ε turbulence model to get the hydraulic performance of a centrifugal pump, the results of the model agreed well with the results of hydraulic test, and the results showed that the clocking effect had a great influence on pressure pulsation and stability of radial force.

To reduce pressure pulsation, a variety of vibration reduction methods and techniques have been developed. HAN et al [6] proposed the application of bionics in hydraulic design to reduce resistance and vibration, which provides a new approach to the study of pressure pulsation in vortex pumps. LIU et al [7] determined that bionic design could effectively reduce resistance compared with traditional design. In recent years, the principle of bionics has been applied to hydraulic machinery and agricultural machinery; CHEN et al [8] studied the silencing principle of eagle owl feathers, applying the structure and sawtooth shape of the feathers to axial fan blades, and revealing the vital function of non-smooth surfaces on drag reduction, noise reduction, and pressure pulsation reduction. In previous studies [9, 10], we studied the influence of jet-flow structure and V-structure grooves on resistance reduction and found that the ability to improve the boundary layer flow state is an important design parameter in bionic modification. KODAMA et al [11] studied the habits of mantis shrimp. To avoid predators and reduce the vibration caused by their movement in the water, mantis shrimp has evolved grooves on their abdomens. These structures are thought to reduce pressure pulsation. It is of great theoretical significance and practical value to apply the principle of bionics to reduce the pressure pulsation of vortex pumps [12-14]. Based on bionics, and considering that vortex pump tongue pressure pulsation was particularly pronounced, the mantis shrimp abdominal segment groove structure was applied to the volute of a vortex pump to create a bionic groove volute. We chose the IS 125-80-230 (LXH) vortex pump as the model pump, established a bionic mantis shrimp groove volute vortex pump fluid domain model, conducted numerical simulation with the model, and studied the effect of the bionic grooves on pressure pulsation.

2 Bionic mantis shrimp groove volute vortex pump model

2.1 Bionic groove structure model

The mantis shrimp is a common marine animal that has evolved a unique body structure, which can effectively reduce the resistance in water, and reduce vibration caused by its own motion. The bottom half of the mantis shrimp’s body is composed of continuous abdominal segments divided into seven sections. There are obvious boundaries, forming a surface groove structure, between the segments. The structure of a mantis shrimp is shown in Figure 1(a). Studies have shown that the mechanism of mantis shrimp’s swimming drag reduction and vibration reduction is mainly due to its non-smooth groove structure surface [15, 16]. The groove structure is composed of high strength calcium abdominal segments and its surface forms an arc-shaped convex while the mantis shrimp is swimming that can improve the streamline over the surface of the shrimp’s body, expand the boundary layer, reduce the change rate of the velocity gradient and thus the resistance caused by the change of the velocity gradient, and effectively reduce vibration, accelerate and stabilize the shrimp’s swimming. Based on the characteristics of these surface structures of mantis shrimp, we measured, analyzed, and researched to develop a bionic mantis shrimp groove structure model. Considering the specific engineering application, the bionic groove structure was optimized and finalized as a semicircular groove structure, radius R=2.5 mm, as shown in Figure 1(b).

Since pressure pulsation at the tongue of the vortex pump volute is the most severe in the whole flow region, the bionic groove structure was applied to this region. Varying numbers of grooves (N=0, 1, 2 and 3), shown in Figure 2, were studied.

2.2 Vortex pump fluid domain model

The model pump was the IS 125-80-230 (LXH) vortex pump, with blades R30-F30, inlet diameter of 125 mm, outlet diameter of 80 mm, and impeller diameter of 230 mm. The flow of the pump under standard conditions is Q=144 m³/s, head H=80 m, net positive suction head (NPSH)=3.6 m, power P=75 kW, and pump speed n=2980 r/min.

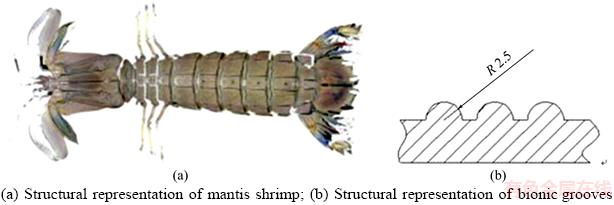
Figure 1 Bionic mantis shrimp model:(Unit: mm)

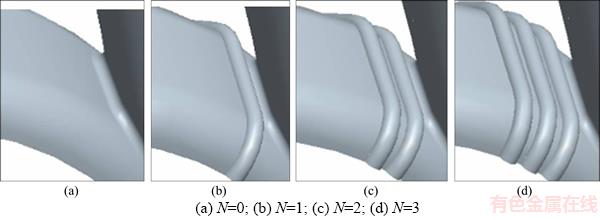
Figure 2 Distribution of vortex pump volute grooves:

The vortex pump fluid domain model included the fluid domain model of the suction chamber, impeller, bionic groove volute, inlet and outlet pipe. The bionic groove volute vortex pump 3-D computational domain model is shown in Figure 3.

Figure 3 Vortex pump fluid domain model

2.3 Turbulence model and boundary conditions

CFD can improve the accuracy of the model by comparing the experimental data [17]. The RNG k–ε turbulence model was used to calculate the unsteady flow field because it uses the mixed function method to generate an analytical formula for viscous flow with a low Reynolds number, which makes the turbulent flow model transition smoothly from the near-wall region to the far-wall region, improving simulation accuracy [18-20]. The pressurized water chamber defined the static coordinate system, and a sliding mesh was applied in the flow passages of the impeller. The SIMPLEC algorithm, based on the finite volume method and two-order upwind scheme dispersed difference equation, was selected to conduct discrete solutions. In the RNG k-ε turbulence model, the turbulent motion satisfies the following Eq. (1) double equation model of turbulent kinetic energy (TKE) dissipation:

                           (1)

where μ_t is the turbulent viscosity coefficient; C_μ is the proportionality constant; ρ is fluid density; k is TKE; and ε is TKE dissipation rate, defined by

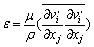                          (2)

where μ is the fluid viscosity coefficient and v is flow field velocity in the mainstream direction.

The transport equation of k and ε can be obtained by the transient N–S equation as:

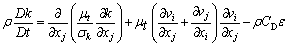 (3)

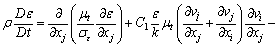
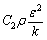                             (4)

where t is time; C_D, C₁ and C₂ are empirical constant; σ_ε is the Prandtl number of ε; σ_k is the effective Prandtl number of turbulent pulsation; and the model constant values C₁=1.44, C₂=1.92, C_μ= 0.085, C_D=1.0, σ_ε=1.3 and σ_k=1.0.

The velocity boundary conditions were adopted as vortex pump inlet boundary conditions; the inlet flow conditions of Q=144 m/s³ was at standard conditions; the outlet used the free exit boundary condition; there are non-slip conditions on each wall; the atmospheric pressure was defined as the reference pressure; and convergence accuracy was 10^–4. The unsteady numerical simulation step was set to 1.678×10^–4, the impeller turned 3° per time step, and the impeller completed one rotation at time step 120.

2.4 Distribution of monitoring point

To analyze the effects of the bionic groove volute and the number of grooves on vortex pump pressure pulsation, it was necessary to define monitoring points on the pump volute. Eight monitoring points were located on the volute; points P₆, P₇ and P₈ were set at the midpoint of the fourth, sixth, and eighth cross-section of volute, respectively. Monitoring points P₁ to P₅ were set every 15°, clockwise from the midpoint of the second cross-section of the volute. Because the pulsation around the tongue was large, a large number of monitoring points were set in the tongue region to conduct a more comprehensive study. Figure 4 shows the distribution of the monitoring points.

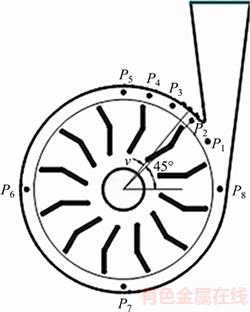
Figure 4 Distribution of monitoring points

2.5 Mesh independent verification

To ensure calculation accuracy, the hybrid mesh technique was employed to divide the unstructured meshes of the vortex pump among its components, namely the suction chamber, impeller, and bionic groove volute. Mesh refinement was used on the surface of the impeller and the connecting edge of the impeller and back plate. For both accuracy and computational efficiency of the numerical simulation, the mesh independence of the computational model was verified at different mesh numbers. The results are shown in Figure 5. When the mesh number m>1.8×10⁶, the head H, shaft power P, and efficiency η of vortex pump were basically stable; the amplitude of variation was not more than 0.5%. Therefore, the total mesh number of model pump is 1.806545×10⁶.

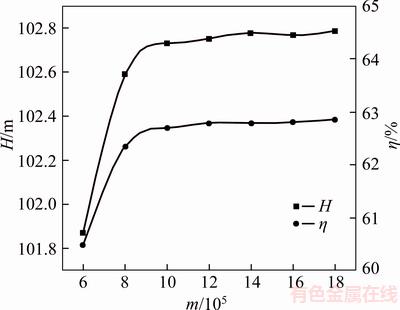
Figure 5 Effect of mesh number on numerical simulation

3 Analysis of bionic groove volute on vortex pump pressure pulsation

The characteristics of the pressure pulsation can be expressed by the pressure pulsation coefficient C_p, which can be calculated by Eq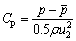.(5):

                             (5)

where p is the instantaneous pressure value; 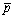is the average pressure value; and u₂ is the circumferential velocity of the impeller outlet.

3.1 Analysis of vortex pump inlet and outlet pressure pulsation

The pump inlet and outlet pressure pulsation time-domain graph is shown in Figure 6. For each value of number of grooves N, the pump inlet and outlet pressure pulsation exhibited periodic pulsation, while the flow through the pump could be regarded as steady. When the groove structure was added to the volute, vortex pump inlet pressure pulsation was relatively slight, which meant that the effect of the bionic grooves on vortex pump inlet pressure pulsation was relatively slight. However,outlet pressure pulsation decreased significantly with grooves, compared to the volute without groove structures, which meant that the bionic groove volute reduced vortex pump outlet pressure pulsation and effectively improved pulsation at the outlet.

Through fast Fourier transform (FFT) [21-23], we obtained the vortex pump inlet and outlet pressure pulsation frequency-domain graph, shown in Figure 7. Impeller speed was 2980 r/min (shaft frequency F=49.67 Hz) and the effect of the impeller blade on the fluid is z times the shaft frequency and its harmonics, so for the number of blades z=12, the blade frequency of 596 Hz. Inlet pressure pulsation mainly existed in the low frequency region of f=49.80 Hz, was greatly affected by shaft frequency and was hardly affected by the blade frequency of the impeller. While outlet pressure pulsation mainly occurred at f=597.6 Hz, with secondary frequency f=49.80 Hz, it illustrated that outlet pressure pulsation was mainly affected by blade frequency and less affected by shaft frequency. Bionic groove volute inlet pressure pulsation increased by about 15%, while outlet pressure pulsation decreased by about 26% vs. the volute without grooves. This illustrated that the bionic groove volute reduced outlet pressure pulsation by effectively suppressing the pressure pulsation due to blade frequency. Meanwhile, increasing of the number of grooves had no obvious effect on pressure pulsation. Additionally, pressure pulsation decreased rapidly after f=597.6 Hz, with only slight pulsation at f=1168.31 Hz.

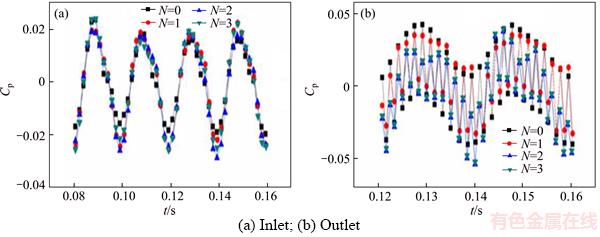
Figure 6 Pump inlet and outlet pressure pulsation time-domain graph:

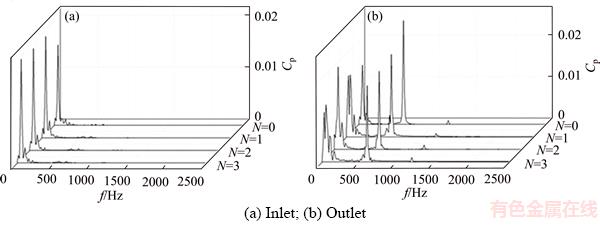
Figure 7 Inlet and outlet pressure pulsation frequency-domain graph:

3.2 Analysis of vortex pump monitoring point pressure pulsation

The data from the last 2 impeller rotations were selected for study, and the time-domain graph of each monitoring point pressure pulsation is shown in Figure 8. During 2 impeller rotations, the pressure at P₁ had 24 peaks and 12 troughs, caused by the dynamic and static interaction between the impeller and the tongue. As shown in Figure 8(a), the pressure pulsation at P₁ was the largest, illustrating that tongue pressure pulsation was the most serious, consistent with the current theory. After adding the groove structure, tongue pressure pulsation had greatly decreased, illustrating that it could effectively reduce tongue pressure pulsation. As shown in Figures 8(b)-(e), pressure pulsation in the region from the tongue to the second cross-section was also serious, but it was slightly lower than that of the tongue, and was also significantly reduced when the groove structure was added.

As shown in Figures 8(f)-(h), pressure pulsation at the monitoring points far from the tongue, namely P₆, P₇ and P₈, had been greatly reduced; the pressure curve became relatively smooth during the whole period, and there was no pressure pulsation.

The frequency-domain graph for each monitoring point pressure pulsation is shown in Figure 9. Pressure pulsation at all monitoring points was concentrated around the shaft frequency of 49.80 Hz and the blade frequency of 597.9 Hz. The reason for the deviation from the actual shaft frequency and blade frequency was the turbulent separation of flow and the interaction between the impeller and the tongue.

As shown in Figure 9(a), at f=597.6 Hz, after adding the groove structures, blade frequency pressure pulsation near the vortex pump tongue region was reduced by 25.9%, which illustrates that the bionic groove structure could effectively reduce vortex pump tongue pressure pulsation. However, increasing the number of grooves had no obvious effect on pressure pulsation.

As shown in Figure 9(b), at P₂ the pressure pulsation coefficient reached its maximum value, and it was also most significantly affected by blade frequency. The impeller would cause a shock to the tongue each time it passed the tongue. Here, there was no obvious difference between the bionic groove volute vortex and the original volute. Comparing Figure 9 (b) with Figure 7 (b), the pressure pulsation at the outlet region was greatly reduced compared to that of tongue region; this was mainly because the outlet diffuser could stabilize and buffer the flow to reduce outlet pulsation.

As shown in Figures 9(c)-(e), pressure pulsation in the region from the tongue to the second cross-section was mainly affected by blade frequency; compared with the original model, there were no obvious changes after adding the bionic groove structure.

As shown in Figures 9(f)-(h), the low frequency region dominated from P₆ to P₈. With each point away from the tongue region, the effect of blade frequency on pressure pulsation was reduced, and the effect of shaft frequency was dominant. In addition, the shaft frequency did not change much at all points in the graph, while shaft frequency pressure pulsation coefficient increased with the addition of grooves. As shown in Figure 9(h), the blade frequency pressure pulsation of P₈ was also reduced by about 25%. This illustrates that the groove structure could reduce the pressure pulsation near the side of the tongue, and the pressure pulsation in this region–especially high frequency pressure pulsation–could be alleviated greatly, to improve the vortex pump stability.

4 Analysis of bionic mantis shrimp groove volute vortex pump flow characteristics

4.1 Effect of bionic groove structure on vortex pump external characteristics

Based on the numerical calculation results, we plotted the flow-head and the flow-efficiency curves for the bionic groove volute vortex pump to get external characteristic curves for different groove numbers, as shown in Figure 10. With the increase of the groove number N, the head H and the efficiency η of the vortex pump decreased slowly. When N=1, the decreases of H and η were each less than 1%, illustrating that the external characteristics were not seriously affected by adding the bionic groove structure.

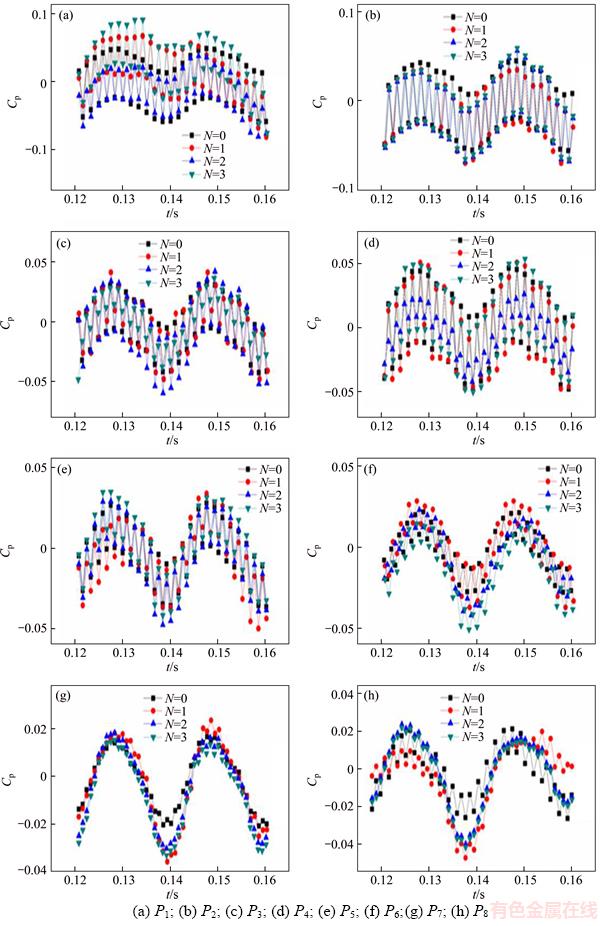
Figure 8 Time-domain graph of pressure pulsation at each monitoring point:

Figure 9 Frequency-domain graph of each monitoring point pressure pulsation:

4.2 Effect of bionic groove structure on vortex pump internal flow characteristics

Since the minimum decrease in vortex pump head and efficiency occurred when the number of grooves N=1, and since increasing the number of grooves had no obvious effect on reducing vortex pump pressure pulsation, atmospheric pressure was taken as the reference pressure to comparatively analyze the instantaneous pressure of a vortex pump only where number of grooves N=1. We selected 4 steps to analyze: the 870th, 900th, 930th and 960th. The phase difference of the impeller between the 4 steps was 90°, and the instantaneous state was 0.25T, 0.50T, 0.75T and 1.0T (T is cycle), respectively, of the eighth cycle. Instantaneous pressure distribution is shown in Figure 11. The pressure at the outlet diffuser pulsated regularly,and that was the main reason for the vibration and noise of the pump. The minimum volute pressure was in the eighth cross-section, and the fluid pressure increased significantly when passing into the tongue and the diffuser; this large pressure difference was also the reason that the pressure pulsation was difficult to suppress.

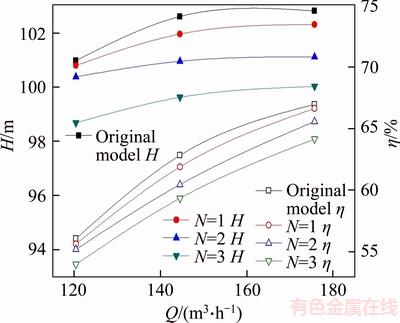
Figure 10 Vortex pump external characteristic curves for different groove number

The velocity vector distribution of the 4 different instantaneous states is shown in Figure 12. Fluid velocity in the impeller was relatively small. Along the radial direction of the impeller the fluid velocity increased rapidly as the impeller worked upon the fluid. In the 3 o’clock direction flow velocity at the impeller outer diameter was the maximum. After entering the diffuser, fluid velocity decreased rapidly, and the kinetic energy of the fluid was converted into pressure energy, due to the pressure amplification characteristic of the diffuser.

The streamline distribution of the 4 different instantaneous states is shown in Figure 13. In the region close to the tongue, fluid mobility of the bionic groove volute was superior, with no vortices. Inside the impeller, from 3 o’clock to 12 o’clock counterclockwise, the internal vortex was forming. From 12 o’clock to 6 o’clock, it was developing and expanding. From 6 o’clock to 3 o’clock , it was collapsing. Then the cycle repeated. The frequent formation and collapse of the vortex in the impeller is the reason for decreased efficiency of the vortex pump. The bionic groove volute improved the flow streamlines of the tongue region, inhibited the formation of vortices, reduced the turbulent bursting energy, decreased velocity, and decreased pressure pulsation, thereby decreasing the pressure pulsation of the vortex pump outlet fluid, improving the pump stability.

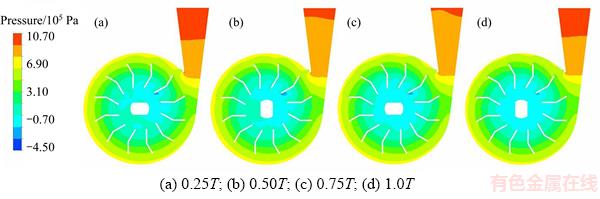
Figure 11 Vortex pump instantaneous pressure distribution:

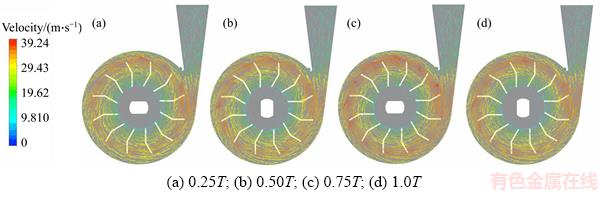
Figure 12 Vortex pump instantaneous velocity vector distribution:

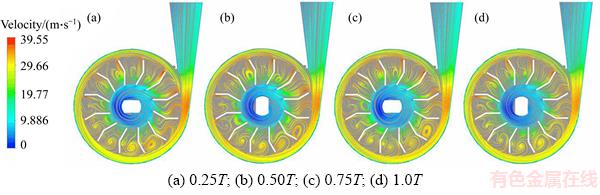
Figure 13 Vortex pump instantaneous streamline distribution:

5 Conclusions

1) A bionic mantis shrimp groove structure can effectively decrease the pressure pulsation at the pump outlet of a vortex pump, mainly by suppressing blade frequency pressure pulsation to decrease the pressure pulsation by 26% compared with the original volute. It can effectively suppress vortex pump pressure pulsation at the tongue region, especially high frequency pressure pulsation, to improve the stability of vortex pump. However, increasing the number of grooves beyond N=1 has no obvious effect on pressure pulsation.

2) There is little effect of the bionic groove structure on the head or efficiency of the vortex pump, and the pump external characteristics are not seriously affected by the bionic groove structure.

3) The flow state of the tongue region is improved by the bionic groove structure, inhibiting formation of vortices and decreasing the turbulent bursting energy, thereby decreasing the pressure pulsation at the tongue region and outlet and improving the system stability of the vortex pump.

References

[1] MINAKOV A V, PLATONOV D V, DEKTEREV A A, SENTYABOV A V, ZAKHAROV A V. The analysis of unsteady flow structure and low frequency pressure pulsations in the high-head Francis turbines [J]. International Journal of Heat and Fluid Flow, 2015, 53: 183-194. DOI: https://doi.org/10.1016/j.ijheatfluidflow.2015.04.001.

[2] ZHAO Zhi-min, WANG Lan, CHEN Hong-zhang. Variable pressure pulsation frequency optimization in gas double- dynamic solid-state fermentation (GDSSF) based on heat balance model [J]. Process Biochemistry, 2015, 50(2): 157-164. DOI: https://doi.org/10.1016/j.procbio.2014.11. 007.

[3] PEI Ji, YUAN Shou-qi, LI Xiao-jun, YUAN Jian-ping. Numerical prediction of 3-D periodic flow unsteadiness in a centrifugal pump under part-load condition [J]. Journal of Hydrodynamics, 2014, 26(2): 257-263. DOI: 10.1016/ S1001-6058(14)60029-9.

[4] ZHANG Ning, YANG Ming-guan, LI Zhong, SUN Xin-kai. Pressure pulsation of centrifugal pump with tilt volute [J]. Journal of Mechanical Engineering, 2012, 48(14): 164-168. DOI:10.3901/JME.2012.14.164.

[5] JIANG Wei, LI Guo-jun, LIU Peng-fei, FU Lei. Numerical investigation of influence of the clocking effect on the unsteady pressure fluctuations and radial forces in the centrifugal pump with vaned diffuser [J]. International Communications in Heat and Mass Transfer, 2016, 71: 164-171. DOI: https://doi.org/10.1016/j.icheatmasstransfer. 2015.12.025.

[6] HAN Xin, ZHANG De-yuan, LI Xiang, LI Yuan-yue. Bio-replicated forming of the biomimetic drag-reducing surfaces in large area based on shark skin [J]. Chinese Science Bulletin, 2008, 53(10): 1587-1592. DOI: 10.1007/ s11434-008-0219-3.

[7] LIU Chun-bao, LI Li, LEI Yu-long, ZHANG Yu-bo. Drag reduction and performance improvement of hydraulic torque converters with multiple biological characteristics [J]. Applied Bionics and Biomechanics, 2016, 3641651. DOI: http://dx.doi.org/10.1155/2016/3641651.

[8] CHEN Kun, LIU Qing-ping, LIAO Geng-hua, YANG Ying, REN Lu-quan, HAN Zhi-wu. Aerodynamic noise reduction of small axial fan using hush characteristics of eagle owl feather [J]. Journal of Jilin University: Engineering and Technology Edition, 2012, 42(1): 79-84. DOI: 10.13229/ j.cnki.jdxbgxb2012.01.035.

[9] GU Yun-qing, FAN Tian-xing, MOU Jie-gang, WU Deng-hao, ZHENG Shui-hua, JIANG Lan-fang, LIU Fu-qing, WANG Evan. Characteristics and mechanism investigation on drag reduction of oblique riblets [J]. Journal of Central South University, 2017, 24(6): 1379–1386. DOI: 10.1007/ s11771-017-3542-5.

[10] GU Yun-qing, MOU Jie-gang, DAI Dong-shun, ZHENG Shui-hua, JIANG Lan-fang, WU Deng-hao, REN Yun, LIU Fu-qing. Characteristics on drag reduction of bionic jet surface based on earthworm's back orifice jet [J]. Acta Physica Sinica, 2015, 64(2):024701. DOI: 10.7498/aps. 64.024701. (in Chinese)

[11] KODAMA K, RAHMAN S M, HORIGUCHI T, THOMAS P. Assessment of hypoxia-inducible factor-1α mRNA expression in mantis shrimp as a biomarker of environmental hypoxia exposure [J]. Biology Letters, 2012, 8(2): 278-281. DOI:10.1098/rsbl.2011.0887.

[12] LOTFABADI P, ALIBABA H Z, ARFAEI A. Sustainability; as a combination of parametric patterns and bionic strategies [J]. Renewable & Sustainable Energy Reviews, 2016, 57: 1337–1346. DOI: https://doi.org/10.1016/j.rser.2015.12.210.

[13] QIN Shi-bin, LEI Yu-tian, BARTH C, LIU Wen-chuen, PILAWA-PODGURSKI R C N. A high power density series- stacked energy buffer for power pulsation decoupling in single-phase converters [J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4905-4924. DOI: 10.1109/TPEL. 2016.2601309.

[14] KADRI U. Prediction of gas-pulsation frequency to reduce slug length in gas/liquid horizontal-pipe flow [J]. SPE Journal, 2015, 20(3): 594-597. DOI: 10.2118/172996-PA.

[15] ROSARIO M V, PATEK S N. Multilevel analysis of elastic morphology: The mantis shrimp’s spring [J]. Journal of Morphology, 2015, 276(9): 1123-1135. DOI: 10.1002/jmor. 20398.

[16] GREEN P A, PATEK S N. Contests with deadly weapons: Telson sparring in mantis shrimp (Stomatopoda) [J]. Biology Letters, 2015, 11(9): 20150558. DOI: 10.1098/rsbl.2015. 0558.

[17] WU Da-zhuan, JIANG Xin-kuo, CHU Ning, WU Peng, WANG Le-qin. Numerical simulation on rotordynamic characteristics of annular seal under uniform and non-uniform flows [J]. Journal of Central South University, 2017, 24(8): 1889–1897. DOI: 10.1007/s11771-017-3596-4.

[18] YU Xian-xian, WANG Yi-wei, HUANG Chen-guang, WEI Yan-peng, FANG Xin, DU Te-zhuan, WU Xiao-cui. Experiment and simulation on air layer drag reduction of high-speed underwater axisymmetric projectile [J]. European Journal of Mechanics B/Fluids, 2015, 52: 45-54. DOI: https://doi.org/10.1016/j.euromechflu.2015.01.002.

[19] LI Jiao, ZHENG Yan-xuan, GONG Pi-hai, GUAN Chang-tao. Numerical simulation and PIV experimental study of the effect of flow fields around tube artificial reefs [J]. Ocean Engineering, 2017, 134: 96-104. DOI: https://doi.org/ 10.1016/j.oceaneng.2017.02.016.

[20] KUMAR A, KIM M H. Effect of roughness width ratios in discrete multi V-rib with staggered rib roughness on overall thermal performance of solar air channel [J]. Solar Energy, 2015, 119(3): 399-414. DOI: https://doi.org/10.1016/ j.solener.2015.06.030.

[21] MOHANTY P K, AHMAD S, ANTIA H M, ARUNBABU K P, CHANDRA A. Fast Fourier transform to measure pressure coefficient of muons in the GRAPES-3 experiment [J]. Astroparticle Physics, 2016, 79: 23-30. DOI: https://doi.org/ 10.1016/j.astropartphys.2016.02.006.

[22] ZHOU Yi-cong, CAO Wei-jia, LIU Li-cheng, AGAIAN S, CHEN C L P. Fast Fourier transform using matrix decomposition [J]. Information Sciences, 2015, 291: 172-183. DOI: https://doi.org/10.1016/j.ins.2014.08.022.

[23] XING Fang-jian, CHEN Hong-wei, XIE Shi-zhong, YAO Jian-ping. Ultrafast three-dimensional surface imaging based on short-time Fourier transform [J]. IEEE Photonics Technology Letters, 2015, 27(21): 2264-2267. DOI: 10.1109/LPT.2015.2461442.

(Edited by FANG Jing-hua)

中文导读

仿虾蛄沟槽蜗壳对旋流泵压力脉动的影响

摘要：为了改善旋流泵的压力脉动，基于仿生学原理，以虾蛄为生物原型，抽取虾蛄腹节处沟槽仿生工程化模型，建立不同沟槽数的仿虾蛄沟槽蜗壳的旋流泵模型。采用数值模拟方法，对不同沟槽数的旋流泵模型进行计算，研究蜗壳沟槽对旋流泵压力脉动的影响。结果表明：仿生沟槽结构对旋流泵外特性造成的影响很小，但仿生沟槽结构可以通过改善旋流泵隔舌部位流体的流线，抑制漩涡的生成，有效地抑制靠近隔舌区域及旋流泵出口处的叶频压力脉动，降低旋流泵整体的压力脉动，提高旋流泵运行稳定性。

关键词：旋流泵；仿虾蛄沟槽；蜗壳；压力脉动；流动特性

Foundation item: Projects(51779226, 51476144) supported by the National Natural Science Foundation of China; Project(2017C31025) supported by Zhejiang Province Department Public Welfare Industrial Projects, China; Project(2016M601736) supported by Postdoctoral Science Foundation of China; Project(1601028C) supported by Postdoctoral Research Funding Plan in Jiangsu Province, China

Received date: 2017-05-25; Accepted date: 2018-01-16

Corresponding author: ZHENG Shui-hua, PhD, Associate Professor; Tel: +86-571-88871053; E-mail: zneu@zjut.edu.cn; ORCID: 0000-0002-7112-2940