文章编号:1004-0609(2013)07-2003-09
基于UPML吸收边界条件的GPR有限元数值模拟
王洪华1,戴前伟1, 2
(1. 中南大学 地球科学与信息物理学院,长沙 410083;
2. 中南大学 地球科学与信息物理学院 有色金属成矿预测教育部重点实验室,长沙 410083)
摘 要:为了进一步减小截断边界对探地雷达(GPR)数值模拟精度的影响、提高复杂GPR地电模型数值模拟的精度,采用具有良好宽频带吸收特性的单轴各向异性完全匹配层(UPML)吸收边界条件与有限单元法(FEM)相结合的算法来模拟GPR波在复杂地电模型中的传播。从GPR满足的波动方程出发,利用伽辽金法导出二维GPR有限元方程。然后,对UPML区域满足的两个频率域旋度方程采用傅里叶变换,推导GPR时间域有限元波动方程及其求解方法,并建立相应的GPR数值模拟算法。应用以上算法编制的程序对两个复杂GPR地电模型进行了正演模拟,得到了相应的雷达剖面图。模拟结果表明:UPML吸收边界条件能够对截断边界处的强烈反射波进行充分的吸收,大大减弱了截断边界处的强反射;FEM能够对复杂的GPR地电模型进行高精度的模拟。基于UPML吸收边界条件的FEM算法能够对复杂的GPR地电模型进行快速、高效的模拟。
关键词:UPML;吸收边界;探地雷达;数值模拟;有限单元法
中图分类号:P631 文献标志码:A
Finite element numerical simulation for GPR based on UPML boundary condition
WANG Hong-hua1, DAI Qian-wei1, 2
(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education, School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)
Abstract: To decrease the influence of truncation boundaries on the GPR numerical simulation precision availably and improve the precision of complex GPR geo-electric model numerical simulation, the FEM, combined with the UPML boundary condition that is good for absorbing broadband, was used to simulate the propagation of GPR wave in complex GPR geo-electric model. Firstly, starting from wave equation satisfying the GPR, Galerkin method was employed to deduce the two-dimension GPR FEM equation; then, based on the two frequency-domain curl equations which conformed in the UPML field, the GPR time-domain FEM wave equation and its solution were deduced by Fourier transform in details, and then the corresponding GPR simulation algorithm was set up. Finally, the program that was compiled by above algorithms was used to forward model the two complex GPR geo-electric models, and two profile maps of the forward models were obtained. The simulated results demonstrate that UPML boundary condition can fully absorb the super-strong reflection wave on the truncation boundaries, and greatly weaken the strong reflection of truncating boundaries. FEM can simulate complex GPR geo-electric model high accurately. Using the FEM algorithm based on UPML boundary condition can simulate the complex GPR geo-electric models quickly and efficiently.
Key words: UPML; ground penetrating radar; numerical simulation; finite element method
探地雷达(Ground penetrating radar,GPR)是探测浅部地质异常体的有效的地球物理方法[1],GPR数值模拟技术一直是该领域理论研究的热点[2]。目前,常用的GPR数值模拟方法主要有射线追踪法(Ray tracing method,RTM)[3]、时域有限差分法(Finite difference time domain,FDTD)[4]、有限单元法(Finite element method,FEM)[5]等。FDTD法历史悠久、发展成熟,在GPR正演模拟中已得到广泛应用[6-9]。刘田新等[10-11]对探地雷达FDTD正演模拟进行了系统而深入的研究。但是,由于FEM具有适合模拟各种复杂地电介质模型、求解过程规范、计算程序通用性强等优点而逐渐在GPR正演模拟中得到应用。底青云等[12-13]借鉴地震波的FEM数值模拟算法,从Maxwell方程组出发,推导GPR波有限元方程,并进行了GPR波有限元正演模拟;谢辉等[14]采用基于等参单元的FEM算法对Pulse天线的GPR模型进行了模拟计算;DAN等[15]采用FEM算法模拟了GPR波在频散介质中的传播;LUBOWIECKA等[16]利用三维FEM算法模拟了GPR信号,并应用于中世纪石拱桥检测中;戴前伟等[17]采用基于透射吸收边界条件的FEM算法实现了二维GPR波的数值模拟,并与改进的Sarma吸收边界条件的吸收效果进行了对比分析。陈承申[18]采用基于混合吸收边界的FEM算法进行了GPR模拟计算,提高了数值模拟的精度。
PML(Perfectly matched layer)及其改进的吸收边界条件目前主要应用于时域有限差分法探地雷达正演模拟:刘四新等[4]采用PML吸收边界条件实现了GPR波在频散介质中的模拟计算;李静等[19]为了提高GPR的模拟精度,采用基于单轴各向异性完全匹配层(UPML)吸收边界条件的高阶FDTD法进行了数值模拟;冯德山等[20]为了突破CFL(Courant Friedrich Levy)条件的约束、提高数值模拟精度,提出了基于UPML吸收边界条件的交替方向隐式时域有限差分(ADI-FDTD)算法,并用于GPR波数值模拟。UPML吸收边界条件具有良好的宽频带吸收特性,FEM适合模拟复杂的模型,基于UPML吸收边界条件的FEM在电磁仿真领域得到了广泛研究[21-22],但是,目前采用基于UPML吸收边界条件的FEM算法的探地雷达数值模拟鲜有文献报道。
为了更有效地减小截断边界对GPR数值模拟的影响、提高数值模拟的精确度及准确性,本文作者对基于UPML吸收边界条件的FEM算法的GPR数值模拟进行研究。在GPR有限元模拟中采用UPML吸收边界条件吸收外向传播波和衰减波,同时克服了采用PML吸收边界条件需要对电磁场进行分裂处理的不足,该方法对内存需求较低且易于编程实现。最后利用编制的程序对两个复杂地电模型进行数值模拟,验证算法的可行性和有效性。
1 GPR波动方程有限元求解
雷达波满足的波动方程如下[13]:
 (1)
(1)
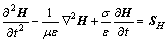 (2)
(2)
式中:E为电场强度;H为磁场强度;ε为介电常数;μ为磁导率;σ为电导率;SE为电场源;SH为磁场源。
有限单元法求解GPR波动方程的实质是求解探地雷达波边值问题(初始、边界条件和偏微分方程)对应的变分问题。以电场满足的波动方程式(1)为例,采用伽辽金法给出基于三角单元剖分的GPR有限元法的详细过程[15]。
第1步 网格剖分
首先,将求解的二维区域剖分成三角形单元,如图1所示。

图1 网格剖分及节点编号示意图
Fig. 1 Sketch map of mesh division and node number
第2步 三角单元线性插值
记三角单元e的3个顶点按逆时针方向分别i、j、m,每个顶点的坐标分别为(xi,yi)、(xj,yj)和(xm,ym),顶点的场值为Ui、Uj和Um,则三角形单元中的场函数为
 (3)
(3)
式中:
 (4a)
(4a)
 (4b)
(4b)
其中:Ni(x,y)、Nj(x,y)和Nm(x,y)为三角单元的形函数,它们是x和y的线性函数;ai,aj,am,bi,bj,bm,ci,cj和cm为只与单元顶点坐标有关的常数;Δ是三角形单元的面积。
第3步 单元积分
根据伽辽金法[23],将式(1)两边同时乘以δE,并求积分,有

 (5)
(5)
式中:E=NTEe,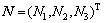 ,
, ;N1、N2和N3是单元上各节点的形函数,E1、E2和E3是各节点的电场值;Ω为单元面积。
;N1、N2和N3是单元上各节点的形函数,E1、E2和E3是各节点的电场值;Ω为单元面积。
则式(5)左边第一项展开为

 (6)
(6)
式中:Me为单元质量矩阵,且
 (7)
(7)
将式(5)左边第二项展开为

 (8)
(8)
式中: 为单元阻尼矩阵,且
为单元阻尼矩阵,且
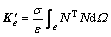 (9)
(9)
将式(5)左边第三项展开为

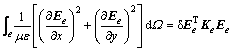 (10)
(10)
式中:
 (11)
(11)
 (12)
(12)
式(5)右边项展开为
 (13)
(13)
第4步 总体合成
根据式(6)、(8)、(10)和(13)得到单元积分为
 (14)
(14)
将单元列向量Ee、 和
和 扩展成全体节点的列向量E、
扩展成全体节点的列向量E、 和
和 ,
,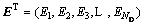 ,
,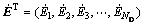 ,
, ,其中:ND是节点总数。将4×4的系数矩阵Me、
,其中:ND是节点总数。将4×4的系数矩阵Me、 和Ke扩展成ND×ND的矩阵M、K′和K,将列向量SE扩展成ND维列向量S,式(14)展开为
和Ke扩展成ND×ND的矩阵M、K′和K,将列向量SE扩展成ND维列向量S,式(14)展开为


 (15)
(15)
式中: ,
, ,
, ,
,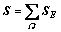 。
。
由于 是任意函数,不恒等于0,则
是任意函数,不恒等于0,则
 (16)
(16)
式(16)为时空域GPR波的二维有限元方程。其 中:M为质量矩阵;K′为阻尼矩阵;K为刚度矩阵; 和为时间的一次导数;
和为时间的一次导数; 和为时间的二次导数。
和为时间的二次导数。
第5步 GPR有限元方程的求解
在对式(16)加载UPML吸收边界条件后,在时间域采用中心差分法离散式(16),对初始条件离散化得到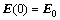 ,
,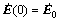 ,假设时窗长度为T,将时间域[0,T]分为几个相等步长
,假设时窗长度为T,将时间域[0,T]分为几个相等步长 ,将t时刻的微分方程记为
,将t时刻的微分方程记为
 (17)
(17)
用中心差商代替微分:
 (18)
(18)
中心差分法是一种条件稳定性的计算方法,当时间步长Δt取值过大时,计算结果就会出现数值色散。为此,本文作者采用 ,其中:ΔXmin为最小单元边长,vmax为最大介质速度,将式(18)代入式(17)整理得
,其中:ΔXmin为最小单元边长,vmax为最大介质速度,将式(18)代入式(17)整理得

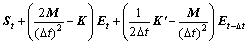 (19)
(19)
式(19)即为GPR有限元正演递推公式。由于0时刻的E0、 和
和 和-Δt时刻的
和-Δt时刻的 、
、 和
和 均为0,所以,根据式(19)可计算出Δt时刻的
均为0,所以,根据式(19)可计算出Δt时刻的 ,然后依次递推可得到所有时刻的E值。令
,然后依次递推可得到所有时刻的E值。令
 (20)
(20)
则式(19)可简化为Ax=B形式的对称正定稀疏的大型线性方程组。
为了高精度、快速求解式(19),选用不完全LU分解预处理的BICGSTAB(Biconjugate gradient stabilized)迭代法进行求解[24]。
2 UPML吸收边界条件
2.1 UPML吸收边界条件的推导
根据电磁波场理论,UPML介质中的Maxwell两个旋度方程可表示为[25-27]
 (21)
(21)
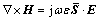 (22)
(22)
其中: 为虚数单位;
为虚数单位; 具有单轴各向异性介质的特征,在二维地电模型中,可表示为
具有单轴各向异性介质的特征,在二维地电模型中,可表示为
 (23)
(23)
式中: 。
。
对式(21)两边求旋度,再代入式(22)可得
 (24)
(24)
式(24)两边同乘矩阵 ,得
,得
 (25)
(25)
将式(23)代入式(25)得

 (26)
(26)
将式(26)左边展开,并采用傅里叶变换转换到时间域,可得
左边=
 (27)
(27)
式(26)右边展开,并采用傅里叶变换转换到时间域,可得

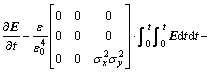

 (28)
(28)
令

 (29)
(29)
则式(26)可写成


 (30)
(30)
根据矢量乘法法则有:
 (31)
(31)
由于ε、μ和σ为坐标的函数,其空间导数可以忽略,则式(30)中右边第二项 。
。
将式(31)代入式(30)后再代入电场源S,整理可得


 (32)
(32)
式(32)即为GPR波在UPML区域满足的波动方程。从式(32)可以看到,当UPML区域的介质为均匀介质时,即 为单位矩阵,矩阵I、J、K和H都为零矩阵,此时式(32)简化为
为单位矩阵,矩阵I、J、K和H都为零矩阵,此时式(32)简化为
 (33)
(33)
采用伽辽金法[15]从式(32)可以推导UPML介质中GPR有限元方程为

 (34)
(34)
其中:
 (35)
(35)
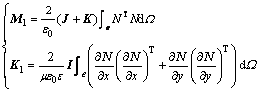 (36)
(36)
 (37)
(37)
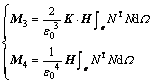 (38)
(38)
采用与式(17)相同的求解方法对式(34)进行求解,即可得到每个时间步的电场值。
2.2 UPML吸收边界条件的吸收效果
为了验证探地雷达FEM正演模拟算法中UPML吸收边界条件的吸收效果,对比在加载和不加载UPML吸收边界条件下雷达波在二维均匀地电模型中的人工截断处的反射波特征,采用如下模型进行正演计算。均匀介质模型区域大小为10 m×10 m,网格间距为0.1 m,UPML区域设置为10层网格,其相对介电常数为ε=3.0,电导率为σ=0.01 S/m,在模型的正 中心(x=5.0 m,y=5.0 m)位置放置一个Riker子波激励源。
图2所示为未加载吸收边界条件下47.5 ns时刻的电场值波场快照。由图2可知,未加载吸收边界条件下电场分量在截断边界的4条边附近产生了强烈的反射波。图3所示为加载UPML吸收边界条件下47.5 ns时刻的电场值波场快照。由图3可知,GPR波波前面以球面波辐射传播,4条边附近没有明显的反射波出现。对比图2和3可知,加载UPML吸收边界条件的探地雷达FEM算法能很好地吸收截断边界产生的强烈的反射波。

图2 未加吸收边界条件的波场快照
Fig. 2 Snapshot of wave field without any boundary condition

图3 加入UPML吸收边界的波场快照
Fig. 3 Snapshot of wave field with UPML boundary condition
3 复杂地电模型模拟算例
3.1 模型一
图4所示为一个尺寸为10.0 m×5.0 m的起伏界面和水平界面组合模型示意图。该矩形区域分为上、中和下3层介质。中间层的上界面为起伏界面,下界面是埋深为1.3 m水平界面。上层介质的相对介电常数ε1为10.0,电导率σ1为0.002 S/m;下层是埋深为1.3 m的水平界面,其相对介电常数ε2为15.0,电导率σ2为0.01 S/m。背景介质的相对介电常数为5.0,电导率为0。空间网格步长为0.1 m,网格总数为100×50,UPML吸收边界设置为10层网格。GPR波脉冲激励源的中心频率为100 MHz,时间步长为0.25 ns,时窗长度为100 ns。采用基于UPML吸收边界条件的FEM算法编制的程序对该模型进行正演模拟,模拟结果为如图5所示GPR正演模拟剖面。由图5可知,在剖面中约37.5 ns时刻,出现一条能量较强起伏反射界面,通过时深转换计算可知,该反射界面与图4模型中起伏界面的位置吻合良好;在62.5 ns时刻,出现近似水平的较强反射界面,通过时深转换计算可知,该反射界面与图4模型中下层界面的位置吻合良好,该近似水平反射界面有轻微起伏,是因为中间起伏界面的影响,使得下层水平界面的反射波与起伏界面的反射波呈相反方向扭曲。同时,由图5的剖面图可知,GPR波在截断边界处的反射极弱,在UPML层几乎被充分吸收。
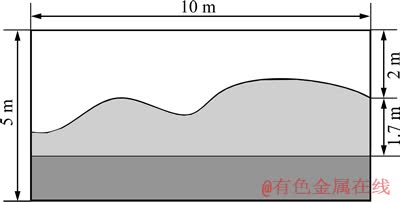
图4 复杂模型1示意图
Fig. 4 Sketch map of complex model 1

图5 复杂模型1 GPR模型正演模拟剖面图
Fig. 5 GPR forward section map of complex model 1
3.2 模型二
图6所示为一个尺寸为10.0 m×5.0 m的三圆和向左拉伸Z字形组合模型示意图。该矩形区域分为 上、下两层介质,中间为一向左拉伸Z字形界面,上层背景介质为素填土,其相对介电常数ε1为5.0,电导率σ1为0.001 S/m,在素填土中存在3个圆状异常体,它们的圆心位置如图6所示,半径为0.3 m,左边为圆状异常体为空洞,中间为金属体,右边为混泥土,其相对介电常数为10.0,电导率为0.000 1 S/m。下层介质的相对介电常数设置为30,电导率为0.01 S/m。空间网格步长为0.1 m,网格总数为100×50,UPML吸收边界设置为10层网格。GPR波脉冲激励源的中心频率为100 MHz,时间步长为0.25 ns,时窗长度为100 ns。应用基于UPML吸收边界条件的FEM算法编制程序对该模型进行正演模拟,模拟结果为如图7所示的GPR正演模拟剖面。由图7可见:3个圆状异常体所在位置出现了双曲线绕射波,只是双曲线两翼的宽度比圆的直径偏大,但双曲线的弧顶能够准确地对应3个圆状异常体的顶点;在55 ns附近有一条能量较强、向左拉伸的Z字形反射界面,通过时深转换计算可以得出它与图6模型中向左拉伸Z字形界面的位置相吻合;此外,可以明显地看到,GPR波在模型截断边界处的反射波非常小,在 UPML层内得到充分的吸收。由此可见,基于UPML吸收边界条件的FEM算法能有效地模拟复杂的GPR模型,模拟所得的正演剖面具有较高的分辨率,有利于指导雷达剖面的数据解译。

图6 复杂模型2示意图
Fig. 6 Sketch map of complex model 2

图7 复杂模型2正演模拟剖面图
Fig. 7 GPR forward section map of complex model 2
4 结论
1) 从探地雷达满足的波动方程出发,采用三角单元剖分的FEM算法推导探地雷达二维有限元方程,给出有限元求解GPR波波动方程的详细步骤。
2) 推导适合FEM算法的UPML吸收边界条件公式,并给出其详细的推导过程,与未加载吸收边界条件的波场快照相比,加载UPML吸收边界条件的 FEM算法大大减弱了截断边界处的超强反射。
3) 两个复杂GPR模型算例结果表明,基于UPML吸收边界条件FEM算法能够精确、高效地模拟复杂GPR模型。
REFERENCES
[1] 曾昭发, 刘四新. 探地雷达原理与应用[M]. 北京: 电子工业出版社, 2010: 168-169.
ZENG Zhao-fa, LIU Si-xin. Ground penetrating radar theory and applications[M]. Beijing: Electronics Industry Press, 2010: 168-169.
[2] 冯德山, 陈承申, 王洪华. 基于混合边界条件的有限元法GPR正演模拟[J]. 地球物理学报, 2012, 55(11): 3774-3785.
FENG De-shan, CHEN Cheng-shen, WANG Hong-hua. Finite element method GPR forward simulation based on mixed boundary condition[J]. Chinese Journal of Geophysics, 2012, 55(11): 3774-3785.
[3] 曾昭发, 高尔根. 三维介质中探地雷达(GPR)波传播逐段迭代射线追踪方法研究和应用[J]. 吉林大学学报: 地球科学版, 2005, 35(S): 119-123.
ZENG Zhao-fa, GAO Er-gen. The 3-D modeling by the segment-by-segment iterative ray-tracing method study of GPR wave[J]. Journal of Jilin University: Earth Science Edition, 2005, 35(S): 119-123.
[4] 刘四新, 曾昭发, 徐 波. 三维频散介质中地质雷达信号的FDTD 数值模拟[[J]. 吉林大学学报: 地球科学版, 2006, 36(1): 123-127.
LIU Si-xin, ZENG Zhao-fa, XU Bo. FDTD simulation of ground penetrating radar signal in 3-dimensional dispersive medium[J]. Journal of Jilin University: Earth Science Edition, 2006, 36(1): 123-127.
[5] 戴前伟, 王洪华, 冯德山, 陈德鹏. 基于双二次插值的探地雷达有限元数值模拟[J]. 地球物理学进展, 2012, 27(2): 736-743.
DAI Qian-wei, WANG Hong-hua, FENG De-shan, CHEN De-peng. Finite element numerical simulation for GPR based on quadratic interpolation[J]. Progress in Geophysics, 2012, 27(2): 736-743.
[6] GOODMAN D. Ground-penetrating radar simulation in engineering and archaeology[J]. Geophysics, 1994, 59(2): 224-232.
[7] SHAARI A, AHMAD R S, CHEW T H. Effects of antenna-target polarization and target-medium dielectric contrast on GPR signal from non-metal pipes using FDTD simulation[J]. NDT & E International, 2010, 43(5): 403-408.
[8] JAMES I, ROSEMARY K. Numerical modeling of ground-penetrating radar in 2-D using MATLAB[J]. Computers and Geosciences, 2006, 32(9): 1247-1258.
[9] 冯德山, 谢 源. 基于单轴各向异性完全匹配层条件的ADI-TDTD三维GPR全波场正演[J]. 中南大学学报: 自然科学版, 2011, 42(8): 2364-2370.
FENG De-shan, XIE Yuan. Three dimensional GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD[J]. Journal of Central South University: Science and Technology, 2011, 42(8): 2364-2370.
[10] 刘四新, 曾昭发, 徐 波. 地质雷达数值模拟中有损耗介质吸收边界条件的实现[J]. 吉林大学学报: 地球科学版, 2006, 35(3): 378-381.
LIU Si-xin, ZENG Zhao-fa, XU Bo. Realization of absorbing boundary condition with lossy media for ground penetrating radar simulation[J]. Journal of Jilin University: Earth Science Edition, 2005, 35(3): 378-381.
[11] 刘四新, SATO M. 井中雷达的数值模拟[J]. 吉林大学学报: 地球科学版, 2003, 33(4): 545-550.
LIU Si-xin, SATO M. Simulation of borehole radar[J]. Journal of Jilin University: Earth Science Edition, 2003, 33(4): 545-550.
[12] 底青云, 王妙月. 雷达波有限元仿真模拟[J]. 地球物理学报, 1999, 42(6): 818-825.
DI Qing-yun, WANG Miao-yue. 2D finite element modeling for radar wave[J]. Chinese Journal of Geophysics, 1999, 42(6): 818-825.
[13] DI Qing-yun, WANG Miao-yue. Migration of ground- penetrating radar data with a finite-element method that considers attenuation and dispersion[J]. Geophysics, 2004, 69(2): 472-477.
[14] 谢 辉, 钟燕辉, 蔡迎春. 电磁场有限元法在GPR正演模拟中的应用[J]. 河南科学, 2003, 21(3): 295-298.
XIE Hui, ZHONG Yan-hui, CAI Ying-chun. Application of finite element methods for electromagnetic fields in forward model of GPR[J]. Henan Science, 2003, 21(3): 295-298.
[15] DAN Jiao, JIN Jian-ming. Time domain finite element modeling of dispersive media[J]. IEEE Microwave and Wireless Components Letters, 2001, 11(5): 220-222.
[16] LUBOWIECKA I, ARMESTO ARIAS J P. Historic bridge modeling using laser scanning, ground penetrating radar and finite element methods in the context of structural dynamics[J]. Engineering Structures, 2009, 31(11): 2667-2676.
[17] 戴前伟, 王洪华, 冯德山, 陈德鹏. 基于三角形剖分的复杂GPR模型有限元法正演模拟[J]. 中南大学学报: 自然科学版, 2012, 43(7): 2668-2673.
DAI Qian-wei, WANG Hong-hua, FENG De-shan, CHEN De-peng. Finite element method forward simulation for complex geoelectricity GPR model based on triangle mesh dissection[J]. Journal of Central South University: Science and Technology, 2012, 43(7): 2668-2673.
[18] 陈承申. 探地雷达二维有限元正演模拟[D]. 长沙: 中南大学, 2011: 28-31.
CHEN Cheng-shen. Two-dimensional finite element forward simulation for ground penetrating radar model[D]. Changsha: Central South University, 2011: 28-31.
[19] 李 静, 曾昭发, 吴丰收. 探地雷达三维高阶时域有限差分法模拟研究[J]. 地球物理学报, 2010, 53(4): 974-981.
LI Jing, ZENG Zhao-fa, WU Feng-shou. Study of three dimension high order FDTD simulation for GPR[J]. Chinese Journal of Geophysics, 2010, 53(4): 974-981.
[20] 冯德山, 陈承申, 戴前伟. 基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟[J]. 地球物理学报, 2010, 53(10): 2484-2496.
FENG De-shan, CHEN Cheng-shen, DAI Qian-wei. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD[J]. Chinese Journal of Geophysics, 2010, 53(10): 2484-2496.
[21] YANSUHIDE T, MAANORI K. Finite element method using port truncation by perfectly matched layer boundary conditions for optical wave guide discontinuity problems[J]. Journal of Light-wave Technology, 2002, 20(3): 463-468.
[22] TSAI H P, WANG Y E, ITOH T T. An unconditionally stable extended(USE) finite-element-time-domain solution of active nonlinear microwave circuits using perfectly matched layers[J]. IEEE Transactions on Microwave Theory and Techniques, 2002, 50(10): 2226-2232.
[23] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994: 266-275.
XU Shi-ze. Finite element method for geophysics[M]. Beijing: Science Press, 1994: 266-275.
[24] 柳建新, 蒋鹏飞, 童孝忠, 徐凌华, 谢 维, 王 浩. 不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J]. 中南大学学报: 自然科学版, 2009, 40(2): 484-491.
LIU Jian-xin, JIANG Peng-fei, TONG Xiao-zhong, XU Ling-hua, XIE Wei, WANG Hao. Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling[J]. Journal of Central South University: Science and Technology, 2009, 40(2): 484-491.
[25] FENG De-shan, DAI Qian-wei. GPR numerical simulation of full wave field based UPML boundary condition of ADI-FDTD[J]. NDT & E International, 2011, 44(6): 495-504.
[26] GEDNEY S D. ZHAO B. An auxiliary differential equation formulation for the complex frequency shifted PML[J]. IEEE Transactions on Antennas Propagation, 2010, 44: 838-847.
[27] LI Jing, ZENG Zhao-fa, HUANG Ling, LIU Feng-shan. GPR simulation based on complex frequency shifted recursive integration PML boundary of 3D high order FDTD[J]. Computers and Geosciences, 2012, 49: 121-130.
(编辑 陈卫萍)
基金项目:国家自然科学基金资助项目(41004053);教育部博士点基金资助项目(20120162110015);中南大学研究生自主探索创新项目(2013zzts053)
收稿日期:2012-10-19;修订日期:2013-03-25
通信作者:戴前伟,教授,博士;电话:0731-88836145;E-mail:qwdai@mail.csu.edu.cn