J. Cent. South Univ. Technol. (2008) 15: 100-105 

DOI: 10.1007/s11771-008-0020-0 

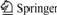
Numerical method of slope failure probability based on Bishop model

SU Yong-hua(苏永华), ZHAO Ming-hua(赵明华), ZHANG Yue-ying(张月英)

(Institute of Geotechnical Engineering, Hunan University, Changsha 410082, China )

Abstract: Based on Bishop’s model and by applying the first and second order mean deviations method, an approximative solution method for the first and second order partial derivatives of functional function was deduced according to numerical analysis theory. After complicated multi-independent variables implicit functional function was simplified to be a single independent variable implicit function and rule of calculating derivative for composite function was combined with principle of the mean deviations method, an approximative solution format of implicit functional function was established through Taylor expansion series and iterative solution approach of reliability degree index was given synchronously. An engineering example was analyzed by the method. The result shows its absolute error is only 0.78% as compared with accurate solution.

Key words: Bishop mechanical model; failure probability of slope; mean deviation method; implicit function; Taylor series; dump of open-pit

1 Introduction

When performing stability analysis of a project, assuming the resistance of structure and the load are known，the safety of structures can be measured by safe margin form, or by safety coefficient form and its logarithm form．In performing uncertainty analysis, limit state equation can be established based on these three forms. However, the resistance of structure and the load of the mining engineering and underground engineering cannot be discriminated definitely. So explicit limit state equation cannot be built up, which leads to the fact that reliability analysis cannot be conducted. Aimed at solving this problem, the response surface method is usually adopted^[1-3]. That is to say, approximate explicit limit state equations are established through finite element method, and then reliability index can be calculated. And this method has gotten great development in recent years^[4-7]. ZHANG et al^[8] proposed response surface method without fitting limit state. SU and FANG^[9], JIMENEZ-RODRIGUEZA et al^[10] analyzed the reliability of adjoining rock and lining of underground engineering with response surface method. All these researches concern the basic principles of response surface method and adopt finite element method to fit limit state. On slope’s mechanical stability, many models have been developed recently. However, in most of these models, the total resistance and the load cannot be expressed through explicit equation and limit
state equations cannot be established. And it is not appropriate to abandon all the effective models that were proved to be true and use finite element method instead of them. And it is difficult to find an all-purpose analysis method at present because different analysis models are suitable for different conditions. Hence, in present study, Bishop’s method was combined with numerical differential method to find an approach to calculate failure probability of slope stability under a certain mechanical model.

2 Functional function based on Bishop mechanical model

2.1 Calculation of stability coefficient

In Bishop’s method of slices, the sliding surface is a circular arc or an approximate circular arc (as shown in Fig.1). Supposing the weight of the slice i is W_i, the force conditions of the slice are statically indeterminate problems. And among all the forces acting on each slice, there are five unknown forces. So slice i is a statically indeterminate problem of second order. According to Bishop’s method, two assumptions can be made: one is ignoring the influence of tangential forces F_i and F_i+1 that act on the sides of the slice, and the other is defining the values of the tangential forces  on the sliding surface.

According to equilibrium condition of the vertical forces on slice i, there exists

Fig.1 Mechanical model of Bishop’s method

            (1)

where  F_i is tangential force of slice i on right side, F_i+1 is tangential force of slice i on left side, W_i is the weight of slice i,  is tangential force on the sliding surface of slice i,  is normal force on the sliding surface of slice i, α_i is obliquity of the sliding surface of slice i, b_i is horizontal width of sliding surface of the slice i,  and  are normal forces of slice i on left side and right side, respectively.

Supposing that a factor of safety is f_S, the shear strength on the sliding surface of slice i only brings into play one part of its service performance. For equilibrium of the sliding surface, the shear resistance τ_i equals the tangential force , namely

                (2)

where  τ_i is the shear strength of slice i , l_i is length of sliding surface of slice i, φ_i is its inner frictional angle and c_i is its cohesion.

The moments of the driving force and the resisting force acting on slice i around O, M_S and M_r, can be calculated by follows, respectively

                     (3)

The safety factor of whole slope corresponded to the sliding surface AHD is as follows:

                   (4)

Substituting Eqn.(2) into Eqn.(1) yields

                  (5)

Substituting Eqn.(5) into Eqn.(4), we get

           (6)

Because F_i and F_{i+1 in} Eqn.(6) are unknown, some problems also exist. In Bishop’s method of slices, the influence of normal forces F_i and F_i+1 that act on the sides of the slice are ignored, that is, F_i+1-F_i=0. Considering the ground vertical load F_Gi and the horizontal force F_Ei(earthquake force etc) that act on each slice, Eqn. (6) can be rewritten as

           (7)

Eqn.(7) is the simplified formula to estimate the stability coefficient of slope based on the Bishop’s simplified method. Note that the term f_S is present on the both sides of Eqn.(7). Hence, it can be calculated by iterative method. In performing random analysis，the general procedure of stability analysis can be illustrated as follows. A group of samples can be sampled from the fundamental random variables with the sampling criterion. A trial value of f_S is chosen, and a new value of f_S will be computed according to Eqn.(7). If the new value of f_S differs substantially from the value originally chosen, the new value of f_S and the sampling fundamental random variables will be substituted into the right of Eqn.(7) at the same time. And another new value of f_S can be calculated. The iterative circulation will not stop until the supposing value of f_S is similar to the new value of f_S. And this is the right stability coefficient that corresponds to the system of sampling parameters.

2.2 Expression of functional function

For simplicity, the fundamental random variables of slope, c_i, φ_i, …, can be written as a system of random vector: X=(X₁, X₂,…, X_n). The stability coefficient is function of random vector. The expression of Eqn.(7) is f_S=f_S(X). According to the relationship between the definition of limit state equation of limit structure and stability coefficient, the general expression can be established as follows

                   (8)

From Eqn.(7), the expression of stability coefficient in performing determination analysis is a nested expression of stability coefficient. So it is impossible to give an explicit expression of limit state equation of structures for Eqn.(8) established according to the expression of stability coefficient. In an effort to solve this problem, response surface method discussed by SU et al^[11] can be adopted. However, the calculation procedure is complicated because a limit state quadrics of approximation needs fitting as response surface method is adopted. Adducing the method that was used to yield the reliability geometric index by using Taylor expansion series in Ref.[8], a new analysis method to calculate failure probabilities of slope directly without fitting a approximate limit state surface was studied in this paper. And the method is applicable to the concrete sliding condition in the Bishop mechanical model.

3 Calculation method of failure probability for slope stability

3.1 Checking point method of failure probability for slope stability

With the indeterminate stability analysis theory, reliability index can be computed as limit state equation is established. Stability index can be given by lots of methods. At present, the general methods are mean point method, first-order second-moment method, checking point method, higher order moment, probability density function method, etc. And checking point method is a better method proposed by International Joint Committee of Structural Safety^[12]. The general procedure of this method can be illustrated as follows:

Assuming X=(X₁, X₂,…,X_n) is mutually independent normal random variables，the limit state Eqn.(8) is performed as a surface in coordinate system OX₁X₂…X_n. We can divide the n dimensional space into two components, the safety zone and the failure zone. Applying random variables submitted to standard normal distribution, we obtain

               (9)

where   is a standardized normal random variable.

Reliability index β describes the shortest distance O?P^* between O?, the origin of standard normal coordinate system, and the limit state surface, which is the length from point P* to go along the directions of the normal of tangent plane of the limit state surface to the origin O?. As the foot of perpendicular, P* is regarded as checking point. Fig.2 shows the condition of three-dimensional normal random variables. The directional cosines of O?P^*, the normal of the limit state surface P*, can be calculated as follows^[13-14]:

        (10)

According to directional cosine, we have

,                      (11)

Correspondingly, P* can be expressed as X*, for P* is a point on the limit state surface, so

                (12)

where  is the means of random variable; and  is the variances of random variable. is the partial derivative at point P*. Using Eqns.(10)-(12), reliability index β and 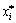 can be calculated． According to the relationships between β and failure probability P_f, we can obtain

                                (13)

In Eqn.(10), the values of partial derivative at the checking points should be calculated. Using analytic method to calculate partial derivative, the functional function f(X₁, X₂,…, X_n) must be explicit function of the fundamental random variables. However because f(X₁, X₂,…, X_n) is implicit function, as seen in Eqns.(7)-(8), partial derivative cannot be calculated by analytic method. At the same time, according to the general procedure of checking point method, the equation of higher degree of β can be established by substituting Eqn.(11) into Eqn.(12). For f(X₁, X₂,…, X_n) is not the explicit expression of stability coefficient, it is also not the explicit expression of β. Finite differential methods and iterative method are adopted to solve the former two problems respectively^[8,15-17].

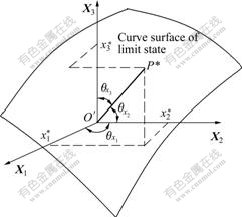
Fig.2 Three-dimensional normal space and checking point

3.2 Calculation of reliability index β by mean deviations method

By supposing that pitch coefficient is α, the mean deviations of one order and second order of the function f(x₁, x₂,…, x_i, …, x_n) to independent variable  can be written as f [x_i-αx_i, x_i] and f [x_i-αx_i, x_i, x_i+αx_i], respectively. With the numerical analysis theory

    (14)

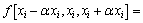
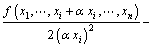
   (15)

for the partial derivative in Eqn.(10),  at the checking point P*, the partial derivative at 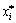 can be approximately replaced by the mean deviations. For partial derivative of one order and mean deviations of one order, we can obtain

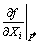
                    (16)

According to Eqn.(7) and Eqn.(8), Eqn.(16) may be written as

So, Eqn.(16) would take the form of

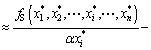
    (17)

Substituting Eqn.(11) into Eqn.(12) yields 

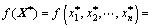
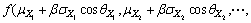
               (18)

In the former equation, the Taylor expansion series of f(β) at β^(k) (the reliability index of kth calculating) can be given. Taking two terms of the Taylor expansion series the values of partial derivative at β^(k) can be given, the iterative equation can be established as follows:

                  (19)

In Eqn.(19), for f(β) is implicit function, according to the derivative theory of composite function, there exists 

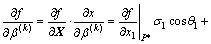
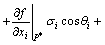
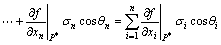
                  (20)

For 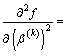 the partial derivative of second order can be approximately replaced by the mean deviations of second order, so we can obtain

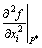
           (21)

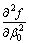
    (22)

Thus the values of partial derivative of implicit function can be calculated on the basis of the mean deviations method, and with the Taylor expansion series and the derivation of composite function, the calculated expression of implicit function can be established. Based on the solutions of the two former problems, the general calculating steps of the reliability index β based on checking point method and iteration method can be described as follows.

1) The mean is chosen as the

first trial value of P*; for general geo-technical engineering, we always chose 3.0 as a trial value of the reliability index β^(k)(when k=0).

2) A  can be calculated by using Eqn.(10), substituting β^(k) into Eqn.（10）, the corresponding random vector can be yielded and then  substituted into Eqn.(7) and Eqn.(8) to iteratively determine .

3) Using Eqn.(17) and Eqn.(22), 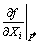and can be calculated respectively; and  can be calculated according to Eqn.(20) and Eqn.(23).

4) Substituting the former values into Eqn.(19), β^(k+1) can be yielded.

5) If |β^(k+1)- β^(k)|≤ε (ε is the  limit error that supposed in advance)，the reliability index is β^(k+1); or, →P*，β^(k+1)→β^(k)，go back to step 2) to continue iterative.

6) Calculating the failure probability of slope by .

4 Computing example analysis

4.1 Brief account of a project

The slope of a dump of open-pit is shown in Fig.3, the bottom is strong weathered strata, the superimposed soil is quaternary clay and sub-clay, about 1 m in thickness, and the slope is 100 m high, the slope angle is 38?. According to geological exploration and repeated calculating by many methods such as the finite element method, the critical slip surface is ABC, which is an approximate circular arc, divided into two components, AB and BC.

The length of circular arc AB is 136 m, and the length of BC is 79 m. The top of AB is constituted with muck，and the bottom goes through the bottom clay stratification. In the muck part ABED, the length of AD is 30 m, the bulk density is 2.1×10³  kg/m³, the mean value of cohesion is c₁=9.8 kPa, the mean of friction coefficient is f₁=0.624 87, the coefficient of variation of cohesion is δ_c1=0.30，the coefficient of variation of friction coefficient is δ_f1=0.12. And in the clay stratification part BCE, the bulk density is         1.87×10³  kg/m³, the mean value of cohesion is c₂=128 kPa, the mean of friction coefficient is f₂=0.487 7, the coefficient of variation of cohesion is δ_c2=0.28, the coefficient of variation of friction coefficient is δ_f2=0.15. According to testing of statistical hypothesis, the cohesion and the friction coefficients of muck and clay don’t refuse normal distribution.

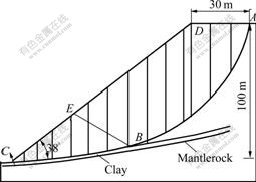
Fig.3 Slope of dump of open-pit

4.2 Compulating process

The dump of open-pit slope is divided into 16 vertical slices. For the variability is small, the bulk density can be regarded as determinative variables, and the uncertainties of inner friction angle and cohesive force are only considered. That is σ_c1=2.94 kPa, σ_f1=0.075, σ_c2=35.84 kPa, σ_f2=0.073 2, and the first trial point can be closed as P*=(c₁ ,c₂, f₁, f₂)=(9.8, 0.624 9, 128, 0.487 7), β⁽⁰⁾=3.0, supposing ε=0.05.

According to the former method, substituting P*=(9.8, 0.624 9, 128, 0.487 7) and f_S=2.0 into Eqn.(7), to iterate and yield f_S=1.243, f(3)=1.674, f′(3)=2.421, f″(3)=1.785. Substituting these values into Eqn.(19) yields β⁽¹⁾=2.491 3. According to the general calculating steps of the reliability index β based on iteration method yields β⁽²⁾=1.9204, |β⁽²⁾- β⁽¹⁾|＞ε; β⁽³⁾=1.694 8, |β⁽²⁾-  β⁽³⁾|＞ε; β⁽⁴⁾=1.624 4, |β⁽⁴⁾- β⁽³⁾|＞ε; β⁽⁵⁾=1.660 9, |β⁽⁴⁾- β⁽⁵⁾|＞ε; β⁽⁶⁾=1.412 9, |β⁽⁶⁾- β⁽⁵⁾|＞ε; β⁽⁷⁾=1.369 1, |β⁽⁶⁾- β⁽⁷⁾|≥ |1.412 9-1.369 1|=0.043 8＜0.05=ε.

And the distance between β⁽⁶⁾ and β⁽⁷⁾ is less than the limit errors that supposed in advance. So the failure probability of the dump of open-pit slope can be calculated as

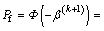
==8.5%

4.3 Comparison of computed precision

Aimed at identifying the accuracy of calculation of the method studied in this paper, Monte Carlo simulation method is adopted, which is based on simulation of Eqn.(7). To perform the simulated calculation, the   1000 00th simulation is regarded as the beginning, and the convergent error controlled is the variety of the failure probability of slope doesn’t exceed 0.01% as 500 simulations are increased. That is, the first calculated failure probability after 100 000 simulations can be

written as , and the 100 500th simulation is , the 101000th simulation is and so on.. If ，it is regarded as convergent, and the failure probability is  According to results of simulation, the failure probability of slope is 9.3%.

Compared with the results of the approximate method studied, the absolute error can be calculated by:

=0.78%

and the relative error can also be obtained as follows:

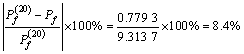
A calculated result from Monte Carlo simulation method is regarded as accurate solution, there is error between result from the approximate method and accurate solution. However, as for general slope structures, such as mine slope, the error can be accepted, therefore precision for the approximate method meets the engineering requirements. The workload of the method is much less than that of the accurate method simultaneously.

5 Conclusions

1) Based on relationship between checking point and reliability index β, differential coefficient of β is changed into partial differential coefficient of each independent variable at checking point. This is an ingenious method to calculate differential coefficient   of β.

2) An iterative calculation format of β is educed by the Taylor expansion series.

3) A new way to calculate reliability index β, namely numerical solution of failure probability, was excogitated through combining iterative calculation format of β with calculation methods of differential coefficient of β.

4) Bishop slice method of slope is regarded as an example, the accomplishing steps of the new way to calculate reliability index β is worked out in detail.

5) A failure probability for a slope is analyzed by the numerical method. The absolute error is 0.78% between accurate solution and the numerical solution.

References

[1] BUCHER C G, BOURGUND U. A fast and efficient response surface approach for structural reliability problems[J]. Structural Safety, 1990, 21(7): 57-66.

[2] RAJASHEKHAR M R, ELLINGWOOD B R. A new look at the response safe approach for reliability analysis[J]. Structural Safety, 1993, 25(l2): 205-220.

[3] GAYTON N, BOURIENT JM, LEMAIRE M. A new statistical approach to the response surface method for reliability analysis[J]. Structural Safety, 2003, 25(1): 99-121.

[4] SCH?ELLER G I. On efficient computational scheme to calculate structural failure probability[J]. Probability Engineering Mechanics, 1989, 4(1): 10-18.

[5] LIU Y W, MOSES F. A sequential response surface methods and its application in the reliability analysis of aircraft structural system [J]. Structural Safety, 1994, 16(2): 39-46.

[6] FARAVELLI L A. Response surface approach for reliability analysis[J]. Journal of Engineering Mechanics, 1989, 115(12): 2763-2781.

[7] WONG F S. Slope reliability and response surface method[J]. Journal of Geotechnical Engineering, 1995, 111(1): 32-53.

[8] ZHANG Xiao-qing, KANG Hai-gui, WANG Fu-ming. A new method for reliability problem without explicit simulation method performance function[J]. Journal of Dalian University of Technology, 2003, 43(5): 650-654. (in Chinese)

[9] SU Yong-hua, FANG Zu-lie. Stability reliability degree analysis of special underground space by improved response surface method[J]. Journal of Rock Mechanics and Engineering, 2000, 19(1): 54 -59.(in Chinese)

[10] JIMENEZ-RODRIGUEZA R, SITARB N, CHACO′N J. System reliability approach to rock slope stability[J]. Int J Rock Mech Min Sci, 2006, 43(6): 847–859.

[11] SU Yong-hua, ZHAO Ming-hua. Application of response surface method in stability reliability degree analysis for slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1417-1425. (in Chinese)

[12] SU Yong-hua, ZHAO Ming-hua, ZHANG Yue-ying. On analysis of reliability of slope stability based on Spencer model by the method of difference[J]. Journal of Rock Mechanics and Engineering, 2006, 25(S1): 2750-2756.

[13] SU Yong-hua, ZHAO Ming-hua, ZOU Zhi-peng. Calculation way of slope stability probability based on disturbing energy method[J]. Journal of Rock Mechanics and Engineering, 2005, 24(19): 3470-3475. (in Chinese)

[14] LILLY P A, LI J. Estimating excavation reliability from displacement modeling[J]. Int J Rock Mech Min Sci, 2000, 37(12): 1261–1265.

[15] XIONG Tie-hua, CHANG Xiao-lin. Application of response surface method in system reliability analysis[J]. Engineering Mechanics, 2006, 23(4): 58-62. (in Chinese)

[16] HE Yue-gang, LI Zhi-wei, YANG Xiao-li. Hazard development mechanism and deformation estimation of water solution mining area[J]. Journal of Central South University of Technology, 2006, 13(6): 738-742.

[17] SU Yong-hua, ZHANG Peng, ZHAO Ming-hua. Improved response surface method and its application in stability reliability degree analysis of tunnel surrounding rock[J]. Journal of Central South University of Technology, 2007, 14(6): 870-877.

(Edited by YANG Hua)

Foundation item: Project(50378036) supported by the National Natural Science Foundation of China; Project(200503) supported by Foundation of Communications Department of Hunan Province, China

Received date: 2007-06-25; Accepted date: 2007-08-25

Corresponding author: SU Yong-hua, Professor, PhD; Tel: +86-731-8821659; E-mail: syh5327@hnu.cn