J. Cent. South Univ. (2019) 26: 120-131

DOI: https://doi.org/10.1007/s11771-019-3987-9

Coupling denoising algorithm based on discrete wavelet transform and modified median filter for medical image

CHEN Bing-quan(陈炳权)^{1, 2, 3}, CUI Jin-ge(崔金鸽)¹, XU Qing(徐庆)¹,SHU Ting(舒婷)², LIU Hong-li(刘宏立)³

1. College of Physics and Electromechanical Engineering, Jishou University, Jishou 416000, China;

2. College of Information Science and Engineering, Jishou University, Jishou 416000, China;

3. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: In order to overcome the phenomenon of image blur and edge loss in the process of collecting and transmitting medical image, a denoising method of medical image based on discrete wavelet transform (DWT) and modified median filter for medical image coupling denoising is proposed. The method is composed of four modules: image acquisition, image storage, image processing and image reconstruction. Image acquisition gets the medical image that contains Gaussian noise and impulse noise. Image storage includes the preservation of data and parameters of the original image and processed image. In the third module, the medical image is decomposed as four sub bands (LL, HL, LH, HH) by wavelet decomposition, where LL is low frequency, LH, HL, HH are respective for horizontal, vertical and in the diagonal line high frequency component. Using improved wavelet threshold to process high frequency coefficients and retain low frequency coefficients, the modified median filtering is performed on three high frequency sub bands after wavelet threshold processing. The last module is image reconstruction，which means getting the image after denoising by wavelet reconstruction. The advantage of this method is combining the advantages of median filter and wavelet to make the denoising effect better, not a simple combination of the two previous methods. With DWT and improved median filter coefficients coupling denoising, it is highly practical for high-precision medical images containing complex noises. The experimental results of proposed algorithm are compared with the results of median filter, wavelet transform, contourlet and DT-CWT, etc. According to visual evaluation index PSNR and SNR and Canny edge detection, in low noise images, PSNR and SNR increase by 10%–15%; in high noise images, PSNR and SNR increase by 2%–6%. The experimental results of the proposed algorithm achieved better acceptable results compared with other methods, which provides an important method for the diagnosis of medical condition.

Key words: medical image; image denoising; discrete wavelet transform; modified median filter; coupling denoising

Cite this article as: CHEN Bing-quan, CUI Jin-ge, XU Qing, SHU Ting, LIU Hong-li. Coupling denoising algorithm based on DWT and modified median filter for medical image [J]. Journal of Central South University, 2019, 26(1): 120–131. DOI: https://doi.org/10.1007/s11771-019-3987-9.

1 Introduction

With the development of digital image processing technology, medical images processing technology with high standard requirements is greatly improved. In the past decades, several imaging techniques were discovered such as CT (computerized tomography) scan, ultrasound, MRI (magnetic resonance imaging), X-ray imaging.These techniques provided the physicians with new information about the interior of the human body was available; however, because of equipment and instrument precision errors, improper operation and other factors, the medical image is easy to be disturbed by noise in the process of collecting. Noise is one of the medical image quality important factors. The noise of medical image may be inaccurate in the diagnosis of diseases, especially cancer diseases and fetus ultrasound. Medical image is the basis of doctors’ diagnosis and treatment, so acquiring high-quality medical image is considered the first step to correct diagnosis.

For the removal of medical image noise, recently, several image processing techniques have been discovered such as MF (median filtering) method [1–3], MW (modified wiener) method [4], AF (average filtering) method [5], and DWT (discrete wavelet transform) [6–9]. MF is a nonlinear digital filtering method based on the order statistical theory, not only has a good inhibitory effect on salt and pepper noise, but also can effectively protect the image edges. The design principle of AF is mainly to weaken the high frequency component of the image and enhance the low frequency component of the image. Generally using it to eliminate the random noise of the image is not as good as using MF for impulse noise. Due to having a good localization in the spatial and frequency domain, DWT is successfully applied for a wide range of image analysis problem and can present any detail of the image. With these preferences in use, its limitations are recorded. 1) Effective only for Gaussian noise. The impulse noise is decomposed by the wavelet transform and the corresponding wavelet coefficients are relatively large at the smaller fine scale, not meeting the condition of the wavelet transform coefficient value is much smaller than signal. 2) Ignoring the smoothness along contours [10]. 3) Providing only limited directional essential information which is an important feature of multi-dimensional signals [11]. In recent years, wavelet transform has shown a clear advantage in the field of signal and image denoising domains, and has many research results. Several new methods based on DWT are proposed, such as contourlet transform [12–14], improved wavelet threshold [15], window-based multi-WT [16], dual-tree complex WT [17], local sparse representation [18]. These methods improve the processing technology of medical image in different degrees, the details of the image and the edge information are protected well. However, generally speaking, most of these methods only work effectively for single noise such as Gaussian noise or impulse noise in medical image. In the practical medical image acquisition, it is generally affected by two kinds of noise, which cannot be completely removed. In this paper, we propose an efficient noise reduction technique for medical image using DWT and modified median filter. Using DWT to process medical image of decomposition sub bands of LL (low low), LH (low high), HL (high low), and HH (high high). Then MF is performed on three sub bands (HL, LH, HH) to remove Impulse noise. Wavelet reconstruction is carried out to get the image after denoising. The advantage of this method is that it combines the advantages of median filter and wavelet to make the denoising more effective.

2 Medical image denoising

In order to remove the Gaussian noise effectively and impulse noise for medical image, simultaneously,and retain the image of the original information as much as possible, in this paper, denoising of mixed noise in medical image is proposed.

2.1 Noise model

According to the properties of noise in practical application, the model can be established by:

             (1)

where f(x) stands for a noisy medical image; s(x) represents the original information of the image; h₁(x) represents the Gaussian noise，is an inherent additive noise that does not change along with the signal; h₂(x) represents the impulse noise, is a random multiplicative noise that varies with the signal. τ₁ and τ₂ are defined as noise level. This model can effectively solve hybrid denoising problem.

2.2 Discrete wavelet transform

For wavelet decomposition of images, the energy is mainly distributed in the low frequency region, noise energy in high frequency region is larger, even more than signal. Therefore, the focus of denoising is still in the high frequency area.

By wavelet, the medical image is decomposed into four sub bands (LL, HL, LH, HH) that stand for horizontal direction and vertical direction. The HL band contains the medical image signal information of high frequency horizontal direction and low frequency vertical direction. The LH band contains the signal information of medical image in horizontal direction of low frequency and vertical direction of high frequency; the last HH band contains high frequency information in both of horizontal direction and vertical direction. Gaussian noise and impulse noise are mainly distributed in high frequency band. From Figures 1 and 2, the LL sub-band continues to be decomposed for the second time after the first decomposition, and the main information of the image is distributed over the LL2 sub-band. The main information of the image is clearly seen from the LL sub-band on second decomposition, while the other sub-bands are only margin and detail. In experiment,the wavelet basis is haar and the level of decomposition is 2.

2.3 Improved wavelet threshold

For Gaussian noise denoising, the wavelet threshold method is widely applied. The traditional threshold denoising method is mainly hard threshold and soft threshold method. However, due to the discontinuity of the threshold point in hard threshold method, the processed image can produce large mean square error and the oscillation occurrence. The soft threshold method estimates the constant deviation between the wavelet coefficients and the actual wavelet coefficients, which makes the processed image too smooth, especially the boundary of the image. A new improved threshold method is proposed in this paper, which can make up the lack of hard threshold and soft threshold, protecting the edge information of image. Noisy images are multi-scale decomposed by wavelet transform time frequency characteristics and multi resolution.

Figure 1 Two-level decomposition of medical image

Figure 2 Two-level decomposition of medical image:

High frequency and low frequency coefficients are present on each sub band, letting the wavelet coefficients below lower threshold approach to 0. other wavelet coefficients are quantitatively processed by the corresponding threshold function. The improved threshold function used in the process of removing Gaussian noise in the image processing module is as follows. The schematic diagram of the improved algorithm is shown in Figure 3.

Figure 3 Schematic diagram of improving threshold function

 (2)

where T represents wavelet threshold; a=0.1; T₀=0.4T; w_i,j is original wavelet coefficients;is coefficient after wavelet transform; sign(·) is the sign function.

                (3)

                  (4)

where σ is the estimate of the level of Gaussian noise; M and N represent the size of the image; L is image decomposition scale. The method is continuous at T or T₀, and the processed image can preserve the edge information of the image.

According to Figure 3, the function has better continuity and derivation. When a=0.1, the upper piecewise function approaches In the lower piecewise function 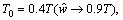if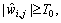the threshold function is continuous at T point, and the high order derivative; else, ifthe upper piecewise function approaches The lower piecewise function approaches 0, obviously; we can judge the threshold function is continuous at point of T.

2.4 Modified median filtering

After wavelet threshold processing, most of the high frequency coefficients of each sub band image are processed, but the reconstructed image still has some individual noise points. The reason is mainly that the impulse noise is larger in the small scale after wavelet transform, so it cannot be quantized by the threshold.

In order to deal with the impulse noise coefficients in the residual coefficients, a modified median filter is proposed in this paper. Through the coupling treatment of the residual coefficient, the image noise is completely removed. During implementation, all pixels according to the gray value from small to large order are in the 3×3 odd filter window. The mean of all the gray values is defined as the center of the window pixels,then calculate the sum of difference with the center pixel, vertical pixels and two diagonal pixels around it，and compare its average with the center pixel by judgement threshold value. Set the coefficients greater than the threshold to zero.

After separating the noise coefficients, the rest are useful coefficients of the medical image. The gray value of the corresponding pixel is retained and the median value is sorted and assigned to each pixel value in the neighborhood to achieve the smoothing of the median filtering. Finally, restructure all the reserved coupling coefficients by wavelet.

As we all know, the wavelet coefficient is the image after the wavelet transform to get the value of each pixel point. In the process of using the modified median filter, the separation of the impulse noise in the image is actually the treatment of the impulse noise coefficients. In this paper, based on the idea of switching threshold [19], the largest and the smallest pixels in the image are removed first, and then the residual noise is further processed by the judgement threshold value to preserve the final signal part. The specific ideas of the algorithm are as follows.

         (5)

where H(i, j) represents center pixels; A(i, j) represents a gray-level image; is average value of the difference between the center pixel and the surrounding pixel.

The following three steps are mainly used:

1) Using 3×3 odd filter window，where H(i, j) represents center pixels.

2) Putting Max(H(i,j)) and Min(H(i,j)) as noise points and marked as 0, others defined as signal points and marked as 1.

3) Observing the value of λ_i (i=1, 2, 3, …, 6). Every λ_i is given by

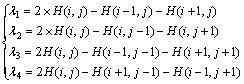      (6)

                           (7)

Comparing the threshold T with(the mean of λ₁–λ₄), when≥T, continue to mark as 0; otherwise, mark as 1.

The steps of the specific threshold method are as follows:

1) The mean ave and variance var of 8 neighbor points adjacent to the center pixel are calculated in filtering window. It can be described as:

                        (8)

              (9)

2) Calculate the absolute value of difference between the center pixel in the window and its neighbor pixels in filtering window. It can be represented by |Δf(i,j)|.

         (10)

                     (11)

where Φ is the mean ofT is optimal threshold in the proposed algorithm.

3) On account of this, we can reorganize pixels marked as 1 to achieve denoising for impulse noise. The filtering window is shown in Figure 4.

Figure 4 3×3 modified median filtering window

3 Algorithm structure analysis

The implementation of the denoising module is as follows (refer to Figure 5):

Step 1: Image acquisition module collects X-ray, ultrasound, CT scan, MRI image by digital imaging device.

Step 2: Image storage module mainly stores image information. It includes image size, color, frame rate, and resolution ratio, etc.

Figure 5 Hardware implementation of denoising system module

Step 3: Image processing module (refer to Figure 6). Part 1: The medical image is decomposed in two levels for four sub-bands by the discrete wavelet, the wavelet threshold is used to quantize the wavelet coefficients larger than the threshold; the remaining part is marked as 0. Part 2: Use modified median filter to process the remaining couple coefficients (Impulse noise). Firstly, the maximum and minimum coefficients in the window are marked as 0, and then the residual coefficients greater than the threshold are still marked as 0, keeping the remaining coefficients.

Step 4: Image restructuring module, in which the residual wavelet coefficients are reconstructed by wavelet, and the denoised image can be obtained.

In fact, there are already some denoising methods for medical image, such as combining the median filter and wavelet. In this paper, coupling coefficients will combine the median filter and wavelet to apply for reducing noise. Timeliness and stability are higher. Figure 6 illustrates the flow of the algorithm in detail. Because the two kinds of noise may affect each other in the removal processing, the two-independent reconstruction is not allowed. After the quantization of the Gaussian noise coefficients by the wavelet, the coupling coefficients are filtered further by the median filter, so that the omission of individual noise coefficients is avoided and the noise reduction is more sufficient.

4 Results and discussion

The proposed algorithm is applied in different medical images datasets, such as X-ray, ultrasound, CT scan, and MRI images. Every image has the same size of 256×256 pixel. In order to verify the performance of the proposed algorithm, two different kinds of noise are added to these medical images [20]. One is an additive noise, such as Gaussian noise; the other is a multiplicative random noise, impulse noise (salt and pepper noise).

In the experimental results, four kinds of medical images are added to white Gaussian noise (variance σ²=10) and impulse noise (densityρ=0.05). Figure 7 shows the coefficient reconstructed image of the four types of medical images that have not undergone median filtering and median filtering after wavelet processing. It is obvious that the individual impulse noise point can be effectively removed after the improved median filter processing as the right of the figure shows, thus, the clarity of the medical image can be improved by wavelet reconstruction.

Figure 6 Schematic diagram of algorithm steps

Figure 7 Multilayer wavelet reconstruction of two-dimensional signals:

Figures 8 to 11 show the subjective visual results corresponding to Figure 7. In experiment, Gaussian noise and impulse noise are added to original medical image. If only the wavelet transform is processed, there are still some noise points in the image, and the wavelet is not effective in suppressing the impulse noise. Therefore, the improved median filtering method is introduced to completely remove the residual noise coefficient, and impulse noise is effectively removal. Observing the last column of each picture, the visual effect of MRI is the best, X-ray and CT follow, ultrasound image is relatively poor.

Figures 12 to 13 show the visual results of X-ray, ultrasound, CT scan, and MRI noisy images after applying the paper algorithm. The performances of the proposed algorithm that is used by objective quantitative index PSNR [21, 22] (peak signal to noise ratio) and SNR (Signal to noise ratio) are shown in Tables 1 and 2, respectively. From visual analysis, it can be analyzed that our proposed algorithm gives more enhanced results in comparison to existing algorithms.

As expected, most noises in the medical image are removed well in the smooth and edges regions. As is shown in Figures 12–13, the effect of DWT-CWT is better than that of DWT because DT-CWT has six decomposition directions to overcome the deficiency of DWT. Considering the redundancy and sparsity of the coefficients, LSR is more delicate in terms of detail, especially in the CT scan images (Rom 3). Relatively, the proposed algorithm has the best denoising effect. In addition, the ultrasound image has additional speckle noise, which makes the processing of the proposed method unsatisfactory. As we all know, traditional median filter can restore the noise-corrupted image well on impulse noise. In order to prove the effectiveness of the proposed method, ρ is increased by 55%. Through visual evaluation, LSR and the proposed method index are relatively high, and the image features are obvious, showing that the proposed algorithm is superior in detail processing.

Figure 8 Visual result of X-ray hand image:

Figure 9 Visual result of ultrasound image:

Figure 10 Visual result of CT scan image:

Figure 11 Visual result of Tumor MRI image:

Figure 12 Visual result of noise image and denoised algorithm for four medical images:

The Canny edge detection algorithm is an optimized edge detection method that connects the refined edges by calculating the edge amplitude, the angle and the double threshold. Both excessive denoising and uncompleted denoising will affect completed information of the edges of the image. Canny edge detection algorithm can effectively reflect the effect of image denoising, which is shown in Figure 14. Compared with ultrasound and CT scan, the contours of X-ray and MRI are more obvious, more delicate and accurate, and the feature capture is more complete. Because the X-ray image is fuzzy, the Canny edge detection effect is not ideal, and the invalid features are captured, which affects the visual evaluation.

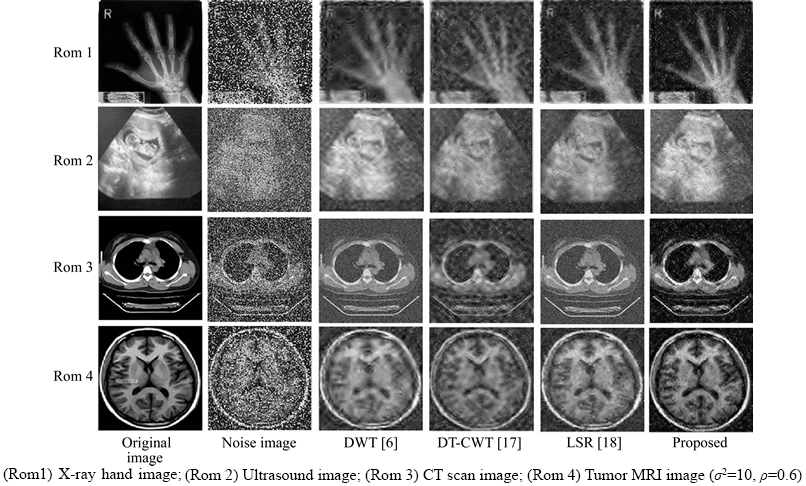
Figure 13 Visual result of noise image and denoised algorithm for four medical images:

Table 1 PSNR value (in dB) of noised and denoised images

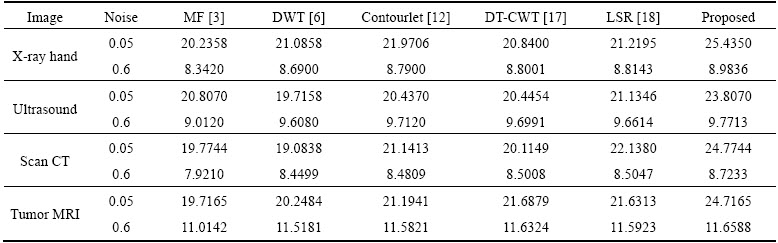
Table 2 SNR value (in dB) of noised and denoised images

Figure 14 Visual result of noise image and denoised image by Canny edge detection algorithm:

The implementation results show enhancement of the medical image quality, which is incorporated with DWT and modified median filter. This method performs well in medical image. In addition, there is a mention that the image recognition is proved by the human eye and PSNR scores, which are not entirely consistent in many experiments. The quality of high PSNR score image may be not necessarily high, mainly because of the sensitivity of the human eye error.

5 Conclusions

In this paper, the removal of Gaussian noise and impulse noise from medical images is based on DWT and modified median filter. It has been discussed and shown how to achieve the denoising of medical image from four modules. The quality enhancement based on edge detection of the medical image is performed in Canny edge detection algorithm. The proposed algorithm has the advantages of enhancing the quality of the denoised image and preserving important features. The experimental results show that the proposed algorithm performs better than the others in both visual impression and quantitative analysis. However, comparing the image of heavy noise pollution, the proposed method is more suitable for the relative small noise variance. Based on the proposed method, the relevant parameters are adaptively adjusted to improve the robustness of the algorithm, which will be the future work for the image with heavy noise pollution.

References

[1] SENEL H G, DAWANT B. Topological median filter [J]. IEEE Trans on Image Processing, 2002, 11(2): 89–104.

[2] SURESH K, PAPENDRA K, MANOJ G, ASHOK K N. Performance comparison of median and wiener filter in image de-noising [J]. International Journal of Computer Applications, 2010, 12(4): 24–28.

[3] PAN Mei-sen, TANG Jing-tian, YANG Xiao-li. A modified adaptive median filter method and its applications in medical images [J]. Biomedical Engineering Applications Basis & Communications, 2012, 22(22): 489–496.

[4] YI San-li, CHEN Zhen-cheng, LING Hong-li. Modified Wiener method in diffusion weighted image denoising [J]. Journal of Central South University, 2011, 18(6): 2001–2008.

[5] HOSSEINI H, HESSAR F, MARVASTI F. Real-time impulse noise suppression from images using an efficient weighted average filtering [J]. IEEE Signal Processing Letters, 2014, 22(8): 1050–1054.

[6] WINK A M, ROERDINK J B. Denoising functional MR images: A comparison of wavelet denoising and Gaussian smoothing [J]. IEEE Transactions on Medical Imaging, 2004, 23(3): 374–87.

[7] HIREMATH P S, AKKASALIGAR P T, BADIGER S. Removal of gaussian noise in despeckling medical ultrasound images [J]. International Journal of Computer Science & Applications, 2013, 1(5): 25–35.

[8] IKEDA M, MAKINO R, IMAI K. A new evaluation method for image noise reduction and usefulness of the spatially adaptive wavelet thresholding method for CT images [J]. Australasian Physical & Engineering Sciences in Medicine, 2012, 35(4): 475–483.

[9] INDULEKHA N R, SASIKUMAR M. An efficient method for denoising medical images using 3D DWT and bilateral filter [J]. International Journal of Innovative Research in Computer and Communication Engineering, 2015, 3(6): 5634–5642.

[10] ZHOU Z F, SHUI P L. Contourlet-based image denoising algorithm using directional windows [J]. Electronics Letters, 2007, 43(2): 92–93.

[11] PAVITHRA R, RAMYA R, ALAIYARASI G. Wavelet based non local means algorithm for efficient denoising of MRI images [J]. International Journal of Advanced Research in Computer and Communication Engineering, 2015(4): 388–392.

[12] ZHOU Z F, SHUI P L. Contourlet-based image denoising algorithm using directional windows [J]. Electronics Letters, 2007, 43(2): 92–93.

[13] SATHEESH S, PRASAD K. Medical image denoising using adaptive threshold based on contourlet transform [J]. Advanced Computing: An International Journal, 2011, 2(2): 52–58.

[14] ALASADI A H. Contourlet transform based method for medical image denoising [J]. Computer Science Journals, 2015, 9(1): 22–31.

[15] TAUJUDDIN N S A M, IBRAHIM R. Enhancement of medical image compression by using threshold predicting wavelet based algorithm [M]// Advanced Computer and Communication Engineering Technology. Berlin: Springer International Publishing, 2015: 755–765.

[16] AMJAD ALI S, VATHSAL S, LAL KISHORE K. An efficient denoising technique for CT images using window based multi wavelet transformation and thresholding [J]. European Journal of Scientific Research, 2010(2): 315–325.

[17] YANGGuang, YEXu-jiong, GREG S, KEEGAN J, MOHIADDIN R, FIRMIN D. Combined self-learning based single-image super-resolution and dual-tree complex wavelet transform denoising for medical images [C]// SPIE Medical Imaging. International Society for Optics and Photonics, 2016.

[18] YANG A F, MIN L, TENG S H, SUN J X. Local sparse representation for astronomical image denoising [J]. Journal of Central South University, 2013, 20(10): 2720–2727.

[19] XU G Y. An efficient switching median filter for the removal of salt and pepper noise [J]. Journal of Anhui University of Science and Technology (Natural Science), 2017, 37(1): 33–39. (in Chinese)

[20] CHANDRIKA SAXENA, DEEPAK KOURAV. Noises and image denoising techniques: A brief survey [J]. International Journal of Emerging Technology and Advanced Engineering, 2014, 4(3): 878–885.

[21] WANG Z, BOVIK A C, SHEIKH H R, SIMONCELLI E P. Image quality assessment: From error visibility to structural similarity [J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612.

[22] CUI J G, CHEN B Q, XU Q, DENG B. A wavelet threshold image denoising algorithm based on a new kind of sign function [J]. Telecommunications Science, 2017(1): 45–52.

(Edited by HE Yun-bin)

中文导读

基于小波变换和改进中值滤波的医学图像耦合去噪算法

摘要：为了克服医学图像采集和传输过程中的图像模糊和边缘丢失现象，提出了一种基于小波变换和改进中值滤波的医学图像耦合去噪方法。该方法由四个模块组成：图像采集，图像存储，图像处理和图像重建。图像采集，获取包含高斯噪声和脉冲噪声的医学图像。图像存储，包括原始图像和处理后图像的数据、参数等信息的保存。在第三模块中，通过小波分解将医学图像分解为四个子带（LL，HL，LH，HH），其中LL为低频部分，LH，HL，HH分别为水平，垂直和对角线高频部分。利用改进的小波阈值处理高频系数，保留低频系数，并在小波阈值处理后对三个高频子带进行改进中值滤波处理。最后一个模块是图像重建，即通过小波重构去噪后的图像。这种方法的优点是结合中值滤波和小波的优点，去噪效果更好，而不是前两种方法的简单组合。通过DWT和改进的中值滤波器系数耦合去噪，对于包含复杂噪声的高精度医学图像处理非常实用。将所提算法的实验结果与中值滤波，小波变换，Contourlet和DT-CWT等方法的结果进行了比较。 根据视觉评价指标PSNR和SNR以及Canny边缘检测得出：在低噪声图像中，PSNR和SNR分别提高10%~15%；在高噪声图像中，PSNR和SNR增加2%~6%。与其他方法相比，该算法取得了较好的结果，为医学诊断提供了重要方法。

关键词：医学图像；图像去噪；小波变换；改进中值滤波；耦合去噪

Foundation item: Project(2016JJ4074) supported by the Natural Science Foundation of Hunan Province, China; Project(14C0920) supported by the Hunan Provincial Education Department, China; Project(61771191) supported by the National Natural Science Foundation of China

Received date: 2017-11-18; Accepted date: 2018-04-17

Corresponding author: CHEN Bing-quan, PhD, Associate Professor; Tel: +86-13907430726; E-mail: cbq2005@yeah.net; CUI Jin-ge; Tel: +86-13141603689; E-mail: cuijingestu@163.com; ORCID: 0000-0003-3075-0999