J. Cent. South Univ. (2016) 23: 1095-1105

DOI: 10.1007/s11771-016-0359-6

Nonlinear dynamics and coupling effect of libration and vibration of tethered space robot in deorbiting process

WANG Ban(王班)¹, GUO Ji-feng(郭吉丰)², FENG Ji-gen(冯吉根)², WANG Jian(王剑)²

1. School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, China;

2. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: In order to control the growth of space debris, a novel tethered space robot (TSR) was put forward. After capture，the platform, tether, and target constituted a tethered combination system. General nonlinear dynamics of the tethered combination system in the post-capture phase was established with the consideration of the attitudes of two spacecrafts and the quadratic nonlinear elasticity of the tether. The motion law of the tethered combination in the deorbiting process with different disturbances was simulated and discussed on the premise that the platform was only controlled by a constant thrust force. It is known that the four motion freedoms of the tethered combination are coupled with each other in the deorbiting process from the simulation results. A noticeable phenomenon is that the tether longitudinal vibration does not decay to vanish even under the large tether damping with initial attitude disturbances due to the coupling effect. The approximate analytical solutions of the dynamics for a simplified model are obtained through the perturbation method. The condition of the inter resonance phenomenon is the frequency ratio λ₁ =2. The case study shows good accordance between the analytical solutions and numerical results, indicating the effectiveness and correctness of approximate analytical solutions.

Key words: tethered space robot; general nonlinear dynamics; deorbiting process; perturbation method; inter resonance phenomenon

1 Introduction

With the appearance of new aerospace mission requirements for the international space station such as on-orbit assembly, space debris removal and on-orbit supply, on-orbit capture technology has become an important technical basis of on-orbit servicing. A tethered space robot (TSR) is always composed of a platform and terminal actuators (tether-nets or tether- grippers). When a target is in an operation distance of TSR, the terminal actuator is ejected to the target and then captures and locks the target [1]. The target can be towed to deorbit according to the mission requirements. In contrast with rigid manipulator arms, TSR is more promising because of varieties of advantages, such as better safety, less influence on the platform，lower consume energy and better fault-tolerance. Recent research attention has been paid to the dynamics and control of TSR. MANKALA and AGRAWAL [2] studied the dynamic modeling and simulation of a tethered robot system during an impact. WILLIMAS [3] studied the mathematical model of in-plane payload capture with an elastic tether and developed an integrated control scheme

that successfully guided the tether to achieve rendezvous with a payload. HU et al [4] derived the dynamics model of TSR under the orbit coordinate system by using Hamilton principle and C-W Equation and proposed a new efficient time-domain algorithm which could solve the system status quickly and accurately. ZHAI et al [5] developed the governing equations of the tether-net system in orbit frame by applying Lagrange equations and an integrated control scheme based on tether tension and thrusters. LIU et al [6] established the dynamics of the tethered combination system based on Lagrange equation and proposed a four-phase deorbit scheme of TSR.

To simplify the analysis, all of the above-mentioned dynamics researches are modeled as two point masses without taking the attitude motion of spacecrafts into consideration. NOHMI et al [7-8] discussed the analytical model and microgravity experiment for attitude control of TSR. HUANG et al [9-11] derived the dynamics model of TSR under the orbit coordinate system and presented several coordinated control schemes of TSR. All these studies on the attitude of the target are performed with the assumption that the platform constantly follows its own circular orbit which would not be influenced by the tether. Some researches on the attitude dynamics model and control for the spinning tethered formation flight are analyzed, taking the attitude of all spacecrafts into consideration with the assumption of all identical spacecrafts in size, mass and inertia property [12-15]. Obviously, the assumption is not suitable for TSR. The space tethered systems will encounter the impact, libration and vibration problems, because of the tether elasticity and the effect of external forces. The previous studies of libration and vibration for space tethered systems are take the tethered space satellites (TSS) as the research objects [16-19]. But in contrast with TSS, TSR has the special characters of short tether length, weak gravity gradient effect, no electrodynamical force and finishing tasks in a short period of time, leading to the uniqueness of motion law under a constant thrust force.

The general dynamics of the tethered combination is established, taking the attitude of spacecrafts and the nonlinear elastic and the tether damping into account in this work. Then, the complex dynamics behavior of the system is simulated and discussed in the deorbiting process under a constant thrust force. At last, the approximate analytical solutions of the combination are obtained through the perturbation method with the assumption that the attitudes of two spacecrafts are under control completely.

2 General dynamics of tethered combination

2.1 Capture process and system description

As shown in Fig. 1, TSR is constituted of a platform, a reel mechanism, a thin tether, a net and several take-up blocks. The reel mechanism is fixed in the platform. In the pre-capture phase, the platform first approaches to the target until a short distance (about 100 m), and then the net is ejected to the target and expanded by the four take-up blocks. When the target is covered totally by the net, the take-up blocks will close the net by rolling up a cord, which connects all four take-up blocks. After some stabilization maneuvers have been imposed by the reel mechanism, the target will be transported to the graveyard orbit by a thrust force in the post-capture phase.

Fig. 1 Capture process of TSR

The focus in this work is the dynamics of the post-capture phase. The double-rigid-body model of the tethered combination in the post-capture phase is established, as shown in Fig. 2. The target m₁ is connected to the platform m₂ by a tether and the attachment points are A and B in the fixed inertial frame (FF) Oxyz. The three axes of FF are defined by unit vectors (e_x, e_y, e_z) and the z axis perpendicular to the paper pointing outward without being displayed. The body-fixed frame of target (BFT) O₁x₁y₁ is chosen to that the x₁ direction is directed from O₁ to A with its origin in the mass center of target O₁. The body-fixed frame of platform (BFP) O₂x₂y₂ is chosen to that the x₂ direction is directed from B to O₂ with its origin in the mass center of platform O₂. The notation F_t is the tether tension force, F₁₂ and F₂₁ are a pair of interaction forces between the target and platform both with the same value of F_t. In order to make the dynamics more general, it is assumed that we can apply a thruster force and torque on the target. F_1x and F_1y are the coordinate components of the thruster force applied on the target, while the torque u₁ exerted on the mass center of the target. F_2x and F_2y are the coordinate components of the thruster force applied on the platform, while the torque u₂ is exerted on the mass center of the platform. R₁ and R₂ are respectively the displacement vector of O₁ and O₂ in FF, while r₁ and r₂ are respectively the displacement vector of A and B in their own body-fixed frame. l₀ is the tether natural length , l the tether length with elasticity, and e_l the unit vector which is aligned with the tether. Let φ₁ be the angle between the tether and target, and φ₂ the angle between the tether and platform. The attitude angles of the combination, target and platform are respectively denoted by θ, α₁ and α₂. The equations α₁=θ+φ₁ and α₂=θ+φ₂ can be obtained from the simple geometrical relationship. The definitions r₁, r₂, u₁, u₂, F_1x, F_1y , F_2x and F_2y are respectively the size of r₁, r₂, u₁, u₂ , F_1x , F_1y, F_2x and F_2y.

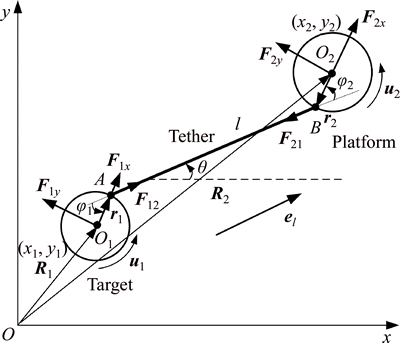
Fig. 2 Model of tethered combination system

General dynamics of the tethered combination is established by the following simplified assumptions:

1) Only the in-plan motion of the tethered combination is considered without taking the out-of- plane motion into account;

2) The tether is massless, taut and straight at all times;

3) The target and platform are modeled as two rigid cylindrical hubs with constant radius;

4) The gravity term is neglected under the assumption that TSR will operate in a quite micro gravity field, e.g. the second Lagrangian point L₂ of the earth- sun system;

5) There are no other external forces affecting the system such as the atmospheric drag, solar light pressure and lunisolar perturbation.

2.2 Nonlinear dynamics of system

The following equations are obtained from the in-plane rigid dynamic formula:

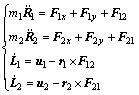                      (1)

where L₁ is the angular momentum of the target on its mass center O₁; L₂ is the angular momentum of the platform on its mass center O₂. The obvious relationship in FF is

                         (2)

where J₁ and J₂ are the moments of inertia of the target and platform; r₁ and r₂ are given by

     (3)

We rewrite the thrust forces in coordinate form as

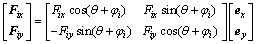 (i=1, 2) (4)

Substituting Eqs. (2), (3) and (4) into Eq. (1), we can get the nonlinear dynamics of the tethered combination as

     (5)

where

 (6)

and ξ=l-l₀ is the tether elastic deformation,m=m₁m₂/ (m₁+m₂) the equivalent mass of the tethered combination. F_t has different expressions for different materials. The dynamic test we conducted of the Kevlar tether indicates that the tether will present strong nonlinear dynamical properties. So we take the quadratic nonlinear elasticity and linear damping into consideration of the Kevlar tether used in our project, and the following expression is obtained as

                    (7)

where k, u and c denote the stiffness, the nonlinear stiffness coefficient and the damping coefficient, respectively. The values of k and c are inversely proportional to the tether length calculated by [20-21]

                              (8)

where E is the elastic modulus, A the tether’s cross section, and σ the damping parameter of the tether material.

We can see from the above general nonlinear dynamics of TSR that the tether elastic deformation ξ, the attitude of tethered combination θ, the angle between the tether and target φ₁ and the angle between the tether and platform φ₂ are coupled with each other. So the system will exhibit complex dynamics behavior in the deorbiting process under a constant thrust force.

3 Simulation results and discussion in deorbiting process

3.1 Standard state and simulation parameters in deorbiting process

We assume that the tethered combination should move along the x axis under the constant thrust force F according to the requirement of the capture mission in the deorbiting process. The destination (x_d, y_d)=(5 km, 0) is 5 km away from the initial position (x₂,y₂)=(0, 0) of the platform. The tether nature length l₀ is constant in the deorbiting process. The disturbances of ξ and its derivative are defined as the position disturbances, and the disturbances of θ, α₁, α₂ and their derivatives as the attitude disturbances. The tethered combination will move along the x axis if there are no any attitude disturbances at the initial time. However, the tethered combination may deviate from direction of the x axis when there are attitude disturbances at the initial time, resulting in the failure of the capture mission. So, it is necessary to study the motion law of the tethered combination under this condition which will be of certain guiding significance for the design of the controller next. We define the initial state without any position disturbances or attitude disturbances that is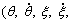 (0, 0, 0, 0, 0, 0, 0, 0) as the standard state as shown in Fig. 3. We set up system parameters as shown in Table 1 according to the capture mission.

It is apparent that there are no attitude motions if the tethered combination is in the standard state in the deorbiting process. The time history of the tether deformation ξ is shown in Fig. 4. It is seen that the tether longitudinal vibration decays dramatically to vanish in about 120 s under the large tether damping. The platform will reach the destination without any deviations, and the duration of the deorbiting process t_f is 1414.2 s.

Fig. 3 Tethered combination in standard state

Table 1 Parameters in simulation

Fig. 4 Time history of tether deformation with standard state

3.2 Influence of different disturbances

Because of the pointing error, the attitude disturbances are cased by capture impacts and the initial angular velocity of the target, the initial state may deviate from the standard state in the actual deorbiting process. The motion law of the tethered combination with different disturbances is studied as followed.

3.2.1 Influence of pointing error

Assuming that there is an initial disturbance of the combination attitude θ=3° caused by the pointing error, the simulation results are shown in Fig. 5. The tether deformation is always positive and the longitudinal vibration decays dramatically to a very small vibration rather than to vanish in a short time even under the large tether damping due to the coupling effect. Then the small vibration sustains in the rest deorbiting process almost without decaying. The tether transverse libration is between 2.6° and 3°. Angles between the tether and two spacecrafts are all between -3° and 3°. So, there is no risk of entangling between the tether and spacecrafts. However, the final displacement of the platform in y direction (y_2f) is 246.5 m, representing the deviation of the tethered combination from the destination.

The simulation results with the disturbance that θ=10° is shown in Fig. 6. In contrast with a disturbance that θ=3°, the tether longitudinal vibration decays dramatically to an approximate stationary vibration. But the amplitude of the approximate stationary vibration is larger and the displacement in y direction is also larger with final value 826.7 m. The greater the initial disturbance of θ is, the greater the approximate stationary vibration and the deviation of the tethered combination from the destination are. But it should be pointed that the tether elastic deformation is positive and the maximum of ξ is far smaller than the distance between the two spacecrafts, which means that there are no risks of tether slack and collision between the target and the platform.

Fig. 5 System response with initial disturbance of combination attitude θ=3°:

Fig. 6 System response with initial disturbance of tethered attitude θ=10°:

3.2.2 Influence of initial angular velocity of target

It is assuming that the target has a small initial angular velocity 0.02 rad/s. So the initial state is =(0, 0, 0, 0, 0, 0.02, 0, 0), and the simulation results are shown in Fig. 7. The attitude angle of the combination θ increases consistently with time to the maximum of about 4.5°. The angle between the tether and target is varied between -6° and 6°, and the angle between the tether and platform is much smaller (within 0.12°). We can see that the tethered combination deviates greatly from the destination with y_2f=137.2 m.

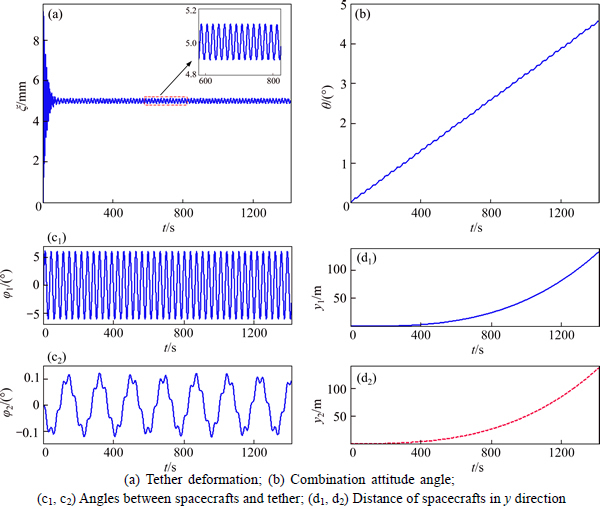
Fig. 7 System response with initial angular velocity of target

The simulation results with an initial angular velocity of the target =0.06 rad/s is shown in Fig. 8. It can be seen that the amplitude of the stationary longitudinal vibration is larger and the attitude angle θ reaches up to about 14° while φ ₁ reaches up to about 20°. The value of y_2f is 404.6 m which also becomes lager. So it is apparent that the initial angular velocity of the target influences the motion of the tethered combination greatly. Moreover, the greater the initial angular velocity is, the greater the deviation and the attitude angles of the combination and target are. If the initial angular velocity of target rises to 0.28 rad/s, the tether is slack and φ ₁ exceeds 90°. The tether and target will be therefore entangled with each other, leading to the failure of the mission.

3.2.3 Influence of initial attitude disturbance of target

Assuming there is an initial attitude disturbance of the target α₁=3° caused by capture impacts, we obtain φ₁=3° due to θ=0. So the initial state is =(0, 0, 0, 0, 3°, 0, 0, 0) and the simulation results are shown in Fig. 9. The tether longitudinal vibration decays dramatically to a very small vibration. The values of θ and φ ₂ are very small, but they are not simple harmonic vibration. The angle between the tether and target vibrates within the initial value 3°. We can see that the tethered combination deviates from the destination with y_2f =0.72 m which is far smaller than the above deviations caused by the initial disturbances of θ and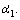

It is apparent that the greater the initial attitude disturbance of the target is, the greater the approximate stationary vibration and deviation from the destination of the tethered combination are. It can be verified by the simulation results with the initial disturbance α ₁=10° in Fig. 10.

3.3 Discussion

From the above simulation results，we know that the initial angular velocity of the target influences the motion of the tethered combination greatly, and the motion amplitude increases with the initial angular velocity of the target. When the initial angular velocity of the target increases to a certain extent, the tether is slack and the angle between the tether and target exceeds 90°, bringing the risks of failure of the mission. Comparatively speaking, the influences of the initial attitude disturbances of the tether and target are smaller because the disturbances cased by the pointing error or capture impacts are always small. However, the initial attitude disturbance of the tether can still lead to a great deviation from the destination of the tethered combination. It must be pointed out that if the constant thrust force disappears abruptly, the tether will be slack and the angle between the tether and target exceeds 90°, bringing the risks of failure, too.

Fig. 8 System response with initial angular velocity of target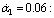

Fig. 9 System response with initial attitude disturbance of target α₁=3°:

Fig. 10 System response with initial attitude disturbance of target α₁=10°:

4 Coupling characteristics of libration and vibration for simple model

4.1 Approximate analytical solutions of combination

The state variables are coupling with each other and the system will exhibit complex dynamics behavior in the deorbiting process under a constant thrust force. In order to prevent the tethered combination deviating from the destination, it is necessary to control the attitude of the target and platform respectively by u₁ and u₂. It is assumed that the attitude disturbances of the target and platform have been eliminated in the deorbiting process and the radius of the target and platform could be ignored in contrast with the tether length. So the combination can be simplified as “space billiard”, as shown in Fig. 11.

Under the assumption that the tether is taut and straight at all times, the problem yields:

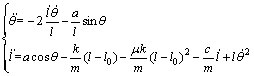     (9)

where a=F/m₂. Equation (9) is a nonlinear differentialequation group with a simple form which is still difficult to be solved directly. We use the perturbation method to obtain the approximate analytical solutions of the tethered combination as followed. The following new parameters are defined as

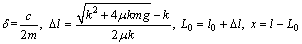 (10)

To understand the basic behavior, small motion is considered. Under the assumption of small motion, we can expand sinθ, cosθ and 1/l into a Taylor series:

             (11)

Applying the perturbation technique [22], we assume that the solution of Eq. (9) can be expressed as a series in x and θ as

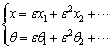                         (12)

Substituting Eqs. (10), (11) and (12) into Eq.(9), we obtain

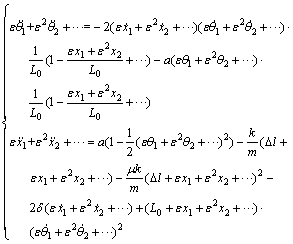 (13)

Equating the coefficients of like powers of x and θ, we obtain:

       (14)

where is the natural frequency of the longitudinal vibration without damping, is the nature frequency of the transverse libration and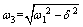is the frequency of the longitudinal damped vibration.

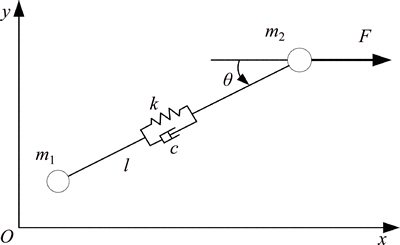
Fig. 11 Simplified model of tethered combination

Substituting the solutions of Eq. (14) into Eq. (12), we obtain:

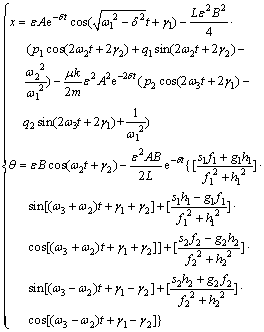   (15)

where

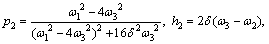
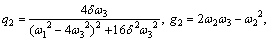
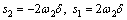                       (16)

and εA, εB, γ₁ and γ₂ can be obtained from the initial conditions. It can be seen that the motion of the tethered combination is controlled mainly by the terms with ε. The whole motion of the combination can be treated as the superposition of the longitudinal damped vibration with frequency of ω₃ and the transverse equal amplitude libration with frequency of ω₂. The basic motion will be modified by terms of ε², which is the coupling effect of two freedoms. It also can be seen from Eq. (15) that the transverse libration does not appear if there is only the longitudinal vibration at the initial time. However, the longitudinal vibration will be caused by the coupling effect even though there is only transverse libration at the initial time. So we get the conclusion that the longitudinal vibration is objective and the transverse libration is avoidable by eliminating the initial disturbance of the transverse libration. To study the stationary motion of the tethered combination, the permanent solution of Eq. (9) can be written individually as

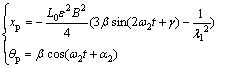      (17)

where is the frequency ratio, 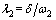is the damping ratio,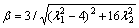is the magnification factor of amplitude and γ=arctan(p₁/q₁)+ 2γ₂ is the phase of the longitudinal vibration. The relation curve of β with respect to λ₁ and λ₂ is given in Fig. 12. It is seen that the value of λ₂ has little effect on β and x_p is almost independent of λ₂ under the condition of λ₁<<2 or λ₁>>2; the value of β will increase significantly under the condition of λ₁→2 which is so-called internal resonance phenomenon and at the same time, the value of λ₂ has significant effect on β, concretely, the value of β will be increased with the decrease of λ₂.

Substituting the expressions of ω₁ and ω₂ into λ₁=ω₁/ω₂, we obtain

Fig. 12 Amplitude-frequency characteristic of tether longitudinal stationary vibration

           (18)

where ε_m=m₂/m₁ is the mass ratio of the platform and target. Because μ and △l are all minute in contrast with l ₀, the approximate expression of λ₁ is given as 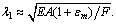To a certain TSR, λ₁ is almost constant with respect to the tether natural length l₀. So the internal resonance phenomenon should be avoided by selecting suitable values of EA of the tether, the mass ratio ε_m and the thrust force F_2x when we design TSR.

4.2 Case study

In order to verify the correctness of approximate analytical solutions, the case study subjects to the initial value (6.9×10^{-3 m, 1.39×10-4 m/s, 10°, 0)r} and the results of approximate analytical solutions and numerical results are shown in Fig. 13. The good accordance between analytical solutions and numerical results indicates the effectiveness and correctness of approximate analytical solutions.

We can see that the longitudinal vibration decays dramatically to the stationary state with the amplitude of 0.3 mm and the transverse libration decays faintly. So the tether damping has great effect on the longitudinal vibration but have little effect on the transverse libration and we should take other measures to decay the transverse libration.

Fig. 13 System response:

5 Conclusions

1) The simulation results show that the four degrees of the tethered combination are coupled with each other in the deoribting process.

2) Comparatively speaking, the initial angular velocity of the target influences the motion of the tethered combination greatly and all the attitude disturbances can cause great deviations from the destination of the tethered combination.

3) The approximate analytical solutions for a simplified model of the combination show the coupling effect of the transverse libration and the longitudinal vibration clearly. The conditions of the inter resonance phenomenon is λ₁ =2.

4) The internal resonance phenomenon should be avoided by selecting suitable values of EA of the tether, the mass ratio ε_m and the thrust force F_2x when we design TSR.

5) In the future, the dynamics and approximate analytical solutions will be validated by experiments in the ground-based flotation platform.

References

[1] ZHAI Guang, QIU Yue, LIANG Bin, LI Cheng. Development of on-orbit capture technology [J]. Robot, 2008, 30(5): 467-480. (in Chinese)

[2] MANKLA K K, AGRAWAL S K. Dynamic modeling and simulation of impact in tether net/gripper systems [J]. Multibody System Dynamics, 2004, 11(3): 235-250.

[3] WILLIAS P. In-plane payload capture with an elastic tether [J]. Journal of Guidance, Control, and Dynamics, 2006, 29(4): 810-821.

[4] HU Ze-hong, HUANG Pan-feng, MENG Zhong-jie. Dynamics modeling and simulation of tethered space robot system [J]. Journal of Astronautics, 2014, 35(1): 28-38. (in Chinese)

[5] ZHAI Gang, QIU Yue, LIANG Bin, LI Cheng. On-orbit capture with flexible tether-net system [J]. Acta Astronautica, 2009, 65(5/6): 613-623.

[6] LIU Hai-tao, YANG Le-ping, ZHANG Qin-bin, ZHU Yan-wei. An investigation on tether-tugging de-orbit of defunct geostationary satellites [J]. Science China Technological Sciences, 2012, 55: 2019-2027.

[7] NOHMI M, YAMAMOTO T, TAKAGI Y. Microgravity experiment for attitude control of a tethered body by arm link motion [C]// Proceeding of IEEE International Conference on Mechatronics and Automation. Harbin: IEEE, 2007: 3519-3524.

[8] NOHMI M, TANIKAWA J, HOSODA T. Simulation analysis of a tethered space robot for space experiment on sounding rocket by JAXA/ISAS [C]// Proceeding of IEEE International Conference on Mechatronics and Automation. Xi’an: IEEE, 2010: 264-269.

[9] HUANG Pan-feng, XU Xiu-dong, MENG Zhong-jie. Optimal trajectory planning and coordinated tracking control method of tethered space robot based on velocity impulse [J]. International Journal of Advanced Robot Systems, 2014, 11: 1-17.

[10] HUANG Pan-feng, WANG Dong-ke, MENG Zhong-jie, LIU Tian-xiong. Post-capture attitude control for a tethered space robot– target combination system [J]. Robotica, 2015, 33(4): 898-919.

[11] HUANG Pan-feng, HU Ze-hong, MENG Zhong-jie. Coupling dynamics modelling and optimal coordinated control of tethered space robot [J]. Aerospace Science and Technology, 2015, 41: 36-46.

[12] CHUNG S J, AHSUN U, SLOTINE J J E. Application of synchronization to formation flying spacecraft: Lagrangian approach [J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 512-526.

[13] CHUNG S J，SLOTINE J J E, MILLER D W. Nonlinear model reduction and decentralized control of tethered formation flight [J]. Journal of Guidance, Control, and Dynamics, 2007, 30(2): 390-400.

[14] MORI O, MATUNAGA S. Formation and attitude control for rotational tethered satellite clusters [J]. Journal of Spacecraft and Rockets, 2007, 44(1): 211-220.

[15] MENON C, BOMBARDELLI C. Self-stabilising attitude control for spinning tethered formations [J]. Acta Astronautica, 2007, 60(10): 828-833.

[16] WANG Xiao-yu, JIN Dong-ping. Quasi-periodic oscillation of a tethered subsatellite with attitude [J]. Journal of Vibration Engineering, 2010, 23(4): 361-365. (in Chinese)

[17] KRUPA M, POTH W, SCHAGERL M. Modelling dynamics and control of tethered satellite systems [J]. Nonlinear Dynamics, 2006, 43(1/2): 73-96.

[18] BUROW A A, TROGER H. The relative equilibria of an orbital pendulum suspended on a tether [J]. Journal of Applied Mathematics and Mechanics, 2000, 64(5): 723-728.

[19] SUN Liang, ZHAO Guo-wei, HUANG Hai, ZHU Ou-ning. Analysis of librational and vibrational characteristics for tethered systems during orbital transfer in plane [J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1245-1254. (in Chinese)

[20] KRUPA M, POTH W, SCHAGERL M, STEINDL A, STEINER W, TROGER H. Modeling, dynamics and control of tethered satellite systems [J]. Nonlinear Dynamics, 2006, 43(1/2): 73-96.

[21] BARKOW B, STEINDL A, TROGER H. A targeting strategy for the deployment of a tethered satellite system [J]. IMA Journal of Applied Mathematics, 2005, 70(5): 626-644.

[22] HE Jin-huan. Homotopy perturbation method: A new nonlinear analytical technique [J]. Applied Mathematics and Computation, 2003, 135(1): 73-79.

(Edited by FANG Jing-hua)

Foundation item: Project(51475411) supported by the National Natural Science Foundation of China; Project(LY15E070002) supported by Zhejiang Provincial Natural Science Foundation of China

Received date: 2015-03-12; Accepted date: 2015-09-23

Corresponding author: WANG Jian, Associate Professor, PhD; Tel: +86-571-87951148; E-mail: usm@zju.edu.cn