Trans. Nonferrous Met. Soc. China 24(2014) 89-99

Titanium cenosphere syntactic foam with coarser cenosphere fabricated by powder metallurgy at lower compaction load

N. JHA¹, D. P. MONDAL¹, M. D. GOEL¹, J. D. MAJUMDAR², S. DAS¹, O. P. MODI¹

1. Advanced Materials and Processes Research Institute, Council of Scientific and Industrial Research, Bhopal 462064, India;

2. Department of Metallurgical and Materials Engineering, Indian Institute of Technology, Kharagpur 721302, India

Received 17 April 2013; accepted 18 June 2013

Abstract: Titanium cenosphere syntactic foam of varying relative densities with coarse cenospheres was developed through powder metallurgy route at lower compaction loads. The cold compaction load was varied in the range of 60 to 75 MPa to obtain the foams of different relative densities. A function of cold compaction load between crushing tendency of cenosphere and relative density was investigated. The compressive deformation behavior of these foams was studied, and empirical relationships among plateau stress, elastic modulus, densification strains and energy absorption are formulated considering their practical significance. The performance indices of the developed foam in comparison with dense titanium were studied and it was found that the foam is superior alternative to titanium for engineering applications.

Key words: titanium foam; cenosphere; relative density; plateau stress; energy absorption

1 Introduction

In past several years, metal foam has emerged as potential material in varieties of applications especially where low density and high energy absorption properties are crucial [1]. Titanium and its alloys are the most attractive materials due to their excellent mechanical properties, biocompatibility and corrosion resistance [2]. Porous titanium inherits the excellent mechanical and biological properties of dense titanium. Further, these foams have special features of porous materials, such as low density, high surface area and high energy absorption capacity. These make titanium foams potentially useful as functional and structural materials. Recent development and advancement of new technologies focus on titanium foams that are considered for both engineering and biomedical applications [2,3].

Research work has been focused on the development of titanium foams fabricated by powder metallurgy route [4-14]. This is due to the fact that titanium is much more difficult to process in liquid state because of its very high melting point (1670 °C). Another problem is its extreme chemical affinity with atmospheric gases (i.e. oxygen and nitrogen), which dissolves rapidly either in liquid or solid titanium at a temperature above 400 °C. Several materials such as carbamide, ammonium bicarbonate, tapioca starch, sodium chloride and magnesium have been attempted by various investigators as temporary space holder in the past [15-19]. Syntactic metal foam can be made using ceramic or metallic micro-balloons as space holders by powder metallurgy route or liquid metallurgy route. These micro-balloons are generally selected from either silicon carbide or aluminum oxide which have high strength and can withstand high compaction pressure [20,21]. Cenospheres are primarily obtained in coal base thermal power plants. These are spherical in shape and hollow in nature, and these materials primarily consist of alumina-silicates (mullite and sillimanite) phases [22,23]. As a result, there is a scope to use these materials as space holders for making syntactic metal foam. MONDAL et al [24] have made an attempt to develop titanium syntactic foam using cenosphere (size of 80-90 μm) as space holder through powder metallurgy route.

Hence, the present investigation is aimed to exploring the possibility of using coarser cenospheres (average size of 150 μm) as space holders to make titanium cenosphere syntactic foam through precise control of cold compaction pressure. Characterization of the developed foams in terms of porosity, density, microstructure, elastic modulus and the yield strength is evaluated along with the effect of cold compaction pressure on foam characteristics.

2 Experimental

Spherical titanium powders (purity of 99.9% and average size of 30±2 mm) are used as matrix materials. Titanium powder and cenospheres in different proportions are mixed uniformly. In order to impart sufficient strength to cold compacted pallets after cold compaction, 2% (mass fraction) water based poly vinyl alcohol (PVA) solution (5% PVA and 95% water) is added in powder mixture as organic binder. The powder mixture is cold compacted at varying applied pressures of 60-75 MPa at a crosshead speed of 0.1 mm/s in a cylindrical die of 20 mm in diameter and 50 mm in height using a universal testing machine (Instron 8801). Pressure is applied for 2 min in order to ensure effectively and uniformly pressing.

The cold compacted pallets are characterized in terms of their dimension and density. The pallets are then dried at 200 °C for 2 h to remove the moisture. Dried pallets are then heated at 400 °C for 2 h followed by heating at 600 °C for 2 h for proper debinding. After debinding, the samples are glass shielded and subjected to sintering. The samples are sintered at a temperature of 1100 °C for 2 h in argon atmosphere. The sintered pallets are examined in terms of their density, porosity, phase analysis, microstructures and compressive deformation behavior. For micro-structural examination, the sintered pallets are polished using standard metallographic method and etched with Keller’s reagent having 20 mL distilled H₂O, 20 mL HNO₃ (70%), 20 mL HCl (38%) and 20 mL HF (40%). The microstructure of the etched pallets is examined by a field emission scanning electron microscope (FESEM, Nova NanoSem 430). The instrument is also interfaced with EDX facility (IE Synergy 250) and the same instrument is used for EDX analysis of the sintered pallets. The density of foam samples is measured through Archimedes’s principle and its porosity is calculated from its theoretical and measured density. The compressive deformation behavior of the samples is carried out using the universal testing machine at a strain rate of 0.01 s^-1. For compression testing, cylindrical samples of 10 mm in diameter and 15 mm in height are used. For each set of relative densities, all tests are repeated thrice for consistency in results and average results are reported herein. The observed variation is less than 3% in each test.

3 Results and discussion

3.1 Raw material

Figure 1(a) shows the microstructure of titanium particles, and it can be observed that these particles are spherical in nature. The size distribution of these particles (Fig. 1(b)) shows a normal distribution. The average size of the particles is (25±5) μm. The cenospheres used in this work are spherical in shape (Fig. 2(a)) and their size distribution is a normal distribution (Fig. 2(b)). The average size of cenospheres is (150±5) μm. It is further noted that the cenosphere shells are porous in nature and the average cenosphere shell wall thickness is 7.2 μm (Fig. 2(c)). The porous nature of cenosphere shell makes it fragile, thus there is a possibility of fracture of cenosphere shell when cold compaction load increases above a critical limit. In our earlier work [24,25], it was noted that when an applied compaction pressure was increased above 75 MPa, the cenosphere breakage started. In the present study, cenosphere size is significantly coarser than that used in earlier study. The cenosphere shell thickness is increased only marginally. It is thus attempted to envisage the behavior of the present sets of cenospheres against varying applied pressure, but surely less than 75 MPa of compaction load used in earlier study.

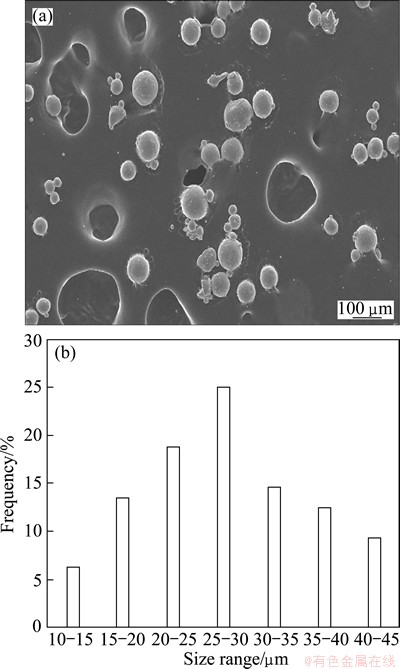
Fig. 1 Microstructure (a) and size distribution (b) of titanium particles

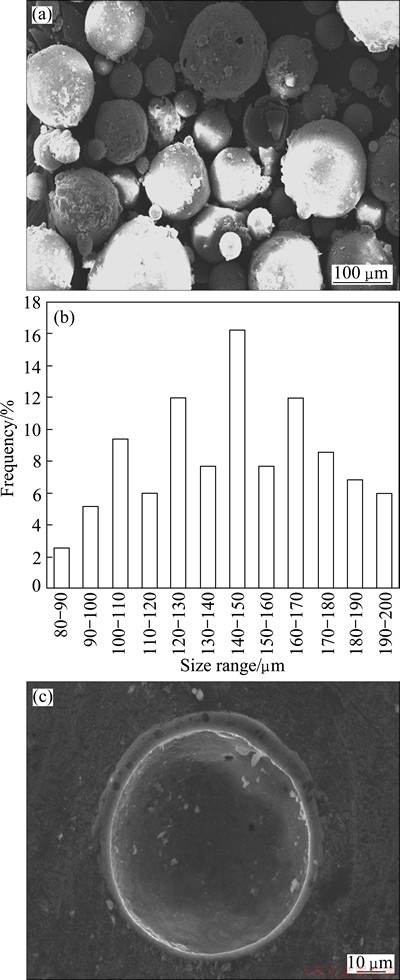
Fig. 2 SEM image (a) and size distribution (b) of cenosphere and high magnification image of cenospshere (c)

3.2 Microstructure

The titanium cenosphere sintered pallets and their microstructure are shown in Figs. 3(a) and (b), respectively. It is noted that the large fraction of cenospheres break during cold compaction when applied pressure is increased to 75 MPa. The cenosphere shell gets accumulated in the sites occupied by the cenospheres and a fraction gets mixed with the titanium powder. After sintering, it makes a composite matrix of titanium cenospheres shell. The SEM image of titanium cenosphere syntactic foams is shown in Fig. 4(a). It is noted that cenospheres are distributed quite uniformly in titanium matrix (Fig. 4(b)). It also shows presence of Ca, Mg, Fe and K in minor quantities in cenosphere shell (Fig. 4(c)). A higher magnification micrograph of titanium cenosphere syntactic foams is shown in Fig. 5(a). It shows that solid smooth network of titanium (region 1) and rough portion where cenosphere shells get accumulated (region 2). The EDX analysis of these two regions also confirms that the region 1 is titanium and region 2 is cenosphere, as shown in Figs. 5(b) and (c). In both cases Al, Si, Ti and O are common. This is due to the fact that: 1) a fraction of cenosphere shell gets fragmented during compaction and is mixed with titanium matrix; 2) during polishing the cenosphere shell gets embedded into titanium matrix and vice-versa. However, the presence of Na, K, Mg and Fe in region 2 confirms that this region is associated with cenosphere shell. It is further noted that finer porosities are present in the titanium matrix network. This is attributed to the presence of porosity in the cold compacted pallets, which gets densified partially after sintering. This confirms that a fraction of micro-porosity remains in such type of foams in addition to the porosity due to cenosphere. This also results in variation of porosity for the foam material.

Fig. 3 Titanium cenosphere sintered pallets (a) and SEM image of titanium cenosphere syntactic foam (b)

Fig. 4 SEM image (a), EDX analysis (b) and elemental surface distribution (c-f) of titanium cenosphere syntactic foam

3.3 Density and porosity of sintered pallets

The density and porosity of these foams are measured following Archimedes principal. The density of crushed cenosphere is also measured through the same technique. The volume fraction of cenosphere (f_c) in titanium syntactic foam is measured using the following equation [26]:

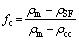                               (1)

where ρ_m is the density of matrix material (i.e. titanium); ρ_SF is the density of titanium syntactic foam; ρ_c is the density of cenosphere particles; and ρ_cc is the density of crushed cenospheres.

The porosity fraction (f_p) of titanium cenosphere foam is determined using the following equations:

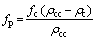                             (2)

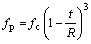                              (3)

where t and R are the cenosphere shell thickness and outer radius of cenosphere, respectively [26].

The density of titanium cenosphere syntactic foam is calculated using the following equation:

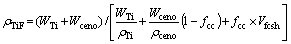    (4)

where ρ_TiF is the density of titanium foam with no porosity other than that with the porosity due to cenosphere; ρ_Ti and ρ_ceno are the densities of titanium and cenosphere, respectively; W_Ti and W_ceno are the mass fractions of titanium and cenosphere in the mixture, respectively; f_cc is the fraction of cenosphere crushed; and r_fcsh is the volume fraction of cenosphere shell in the cenosphere.

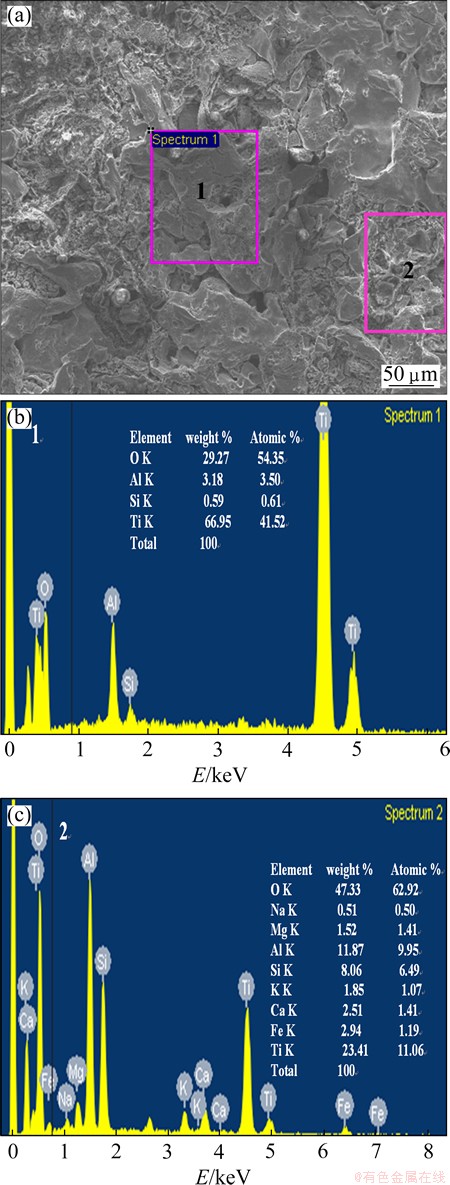
Fig. 5 High magnification micrograph (a) of titanium cenosphere syntactic foam and EDX analysis of region 1 (b) and region 2 (c)

The porosity (η) of the titanium cenosphere foam is calculated from the following equation:

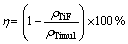                        (5)

where ρ_Timul is calculated from the mass ratio and density of cenosphere and titanium particles, and that of cenosphere shells.

The density of titanium mullite composite comes to be 3.65 g/cm³. The relative density values calculated using these equations are compared with the measured relative density (ρ_df) of the foam (Table 1). It is noted that relative density of foam calculated using Eq. (4) is in good agreement with experimentally measured value. But, the relative density calculated using Eqs. (2) and (3) are marginally lower than experimental value. However, the overall variation is in the range of 5% to 10%. This is attributed to the fact that the crushing effect of cenosphere in foam has been already considered in the measurement of foam density, and thus it is involved implicitly in all equations. When cenospheres are crushed, density of the foam will be higher, and thus σ_sf increases with increase of applied pressure, even though the W_Ti and W_ceno remain constant. This is primarily because of increase of extent of cenosphere crushing. The extent of cenosphere crushing can be predicted by Eq. (4). The predicted value of cenosphere crushing with load is reported in Table 1.

The fraction of crushed-cenosphere increases with increase of compaction load. Even though there are porosities due to cenosphere in the titanium matrix, the experimental measured density of foam is higher than calculated value by Eq. (4). This is attributed to the relatively large extent of fracture of cenospheres. Fracture of cenospheres is shown in Fig. 6. This figure also demonstrates that even though the cenospheres are broken into pieces, they are strongly bonded with the titanium matrix and held in the porosity of the cenospheres prior to its fracture. These holes are primarily giving the porosity in these foams. Because of fragmentation of cenospheres, the pores are not perfectly spherical. However, a good and effective bonding between titanium particles takes place, which leads to more effective sintering compared with our earlier study [24].

Table 1 Relative density and extent of cenosphere crushing under different cold compaction pressures by Eqs. (2-4)

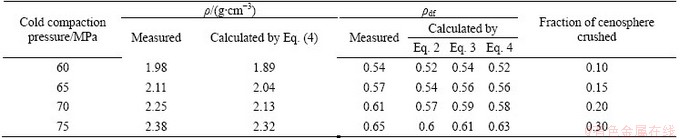
Fig. 6 Microsrtucture of fractured titanium cenosphere syntactic foam

During sintering, a fraction of titanium gets oxidized and this is visible from the XRD pattern of sintered titanium cenosphere foam (Fig. 7). It is further noted from diffraction pattern that foam primarily contains mullite, quartz, TiO₂ and Ti. However, no traces of Na, K and Ca are observed. This is due to the presence of negligible amount of Na, Ca and Mg bearing silicates or oxides in cenospheres. In titanium foam, only 33% (mass fraction) cenosphere is used, and thus the concentration of these elements in titanium cenosphere foam is reduced significantly, which is not detectable by X-ray diffraction. But through EDX analysis, these are detectable in localized regions or as a whole and thus observed in this analysis. However, about 10% of titanium is oxidized during sintering [24].

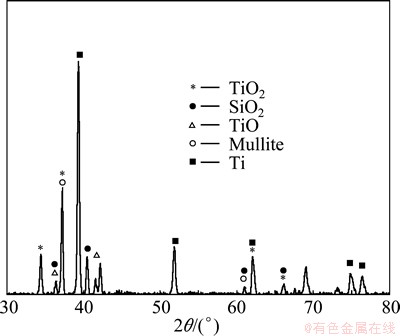
Fig. 7 XRD pattern of sintered titanium cenosphere syntactic foam

3.4 Compressive deformation behavior

The compressive stress-strain curves for titanium foams with different densities are depicted in Fig. 8. It is evident from this study that, the stress-strain curves of these foams follow the typical nature of the stress-strain curves of foam materials [27,28], i.e. a linear elastic region, a flat plateau region and a densification region. These graphs are quite different from those reported in our earlier study [24]. After yielding, the titanium cenosphere foam sample gets collapsed without showing any plateau and densification region. This may be because of inefficient sintering of titanium cenosphere foam in earlier case where applied pressure was quite high (75 MPa) and sintering was carried out at lower temperature. In the present study, applied pressure is varied from 60 to 75 MPa and the sintering is carried out for a longer period of 2 h at a higher temperature of 1100 °C. This leads to higher degree of surface to surface contact and finally to more efficiently sintering, as shown in (Fig. 3(b)).

It is interesting that, when relative density is lower than 0.61, there is gradual drop of stress value after the linear elastic region and this tendency is increase at lower relative density. This is primarily because of relatively high extent of porosity and relatively poor degree of sintering. It is further noted that in plateau region, oscillation of stress is very less, almost undetected. This is due to the finer size of porosity in these foams. The porosity is dictated by the size of cenospheres. The size is expected to be less than 150 μm as the average size of cenosphere is 150 μm and the coarser cenospheres are subjected to fracture to a greater extent. When the relative density increases to more than 0.61, the stress in the plateau region is almost flat and it does not decrease after linear region. In fact, there is marginal increasing trend of stress with strain prior to densification. Here, the plateau stress is considered to be the stress at the end of initial linear region, which could be related to the yield stress of the matrix material. The densification strain is considered the strain at which the foams starts densifying. However in every case, the stress gradually starts increasing, indicating gradual densification. Thus, it is difficult to indicate the densification strain absolutely. In the present analysis, the densification strain is considered the strain corresponding to the intersection of the tangent at the point of sharp increase of stress with strain and the flat line indicating average stress in the plateau region, as shown in Fig. 8. The stress in the plateau region does not oscillate because foam deforms layer by layer. The layer would be of extent of average of the cenosphere size. If it is converted to densification strain, the strain corresponding to its full compaction comes to be less than 0.01. Within this limit of strain, cenospheres gets fractured and compacted. Therefore, as soon as the cenosphere gets fractured, it gets compacted (the cenosphere shell thickness is around 7.2 μm). In the present investigation during compaction, the cenosphere gets fractured substantially and mainly gets accumulated in its void space. Thus, while the titanium cenosphere is compressed, these broken cenospheres and shells provide some resistance against the collapse of the titanium networks or remaining cenosphere shells. The stress is not reduced much during its compression, layer by layer. Similar nature of smooth curves is also observed in open cell foams with fine pore structure [25].

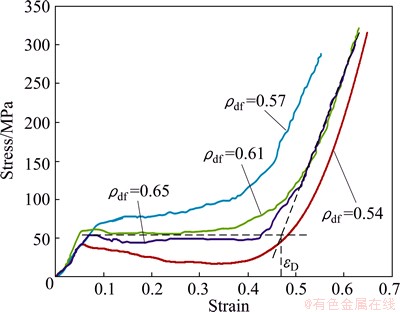
Fig. 8 Stress-strain curve of titanium cenosphere foam at a strain rate of 0.01 s^-1

3.4.1 Effect of relative density on plateau stress

The plateau stress as a function of relative density is reported in Fig. 9. The variation in plateau stress and relative density is shown through error bar. It is noted that the variation in density is 5%, but that in plateau stress is more than 15%. This is attributed to the variation in distribution of cenospheres, density and extent of sintering. Average plateau stress (σ_P1) is increasing with increase of relative density, and follows a power law relationship with relative density. This is obtained through the best fit plot of the measured data. The variation of plateau stress can be expressed in terms of the following equation:

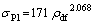                             (6)

The proportionality constant is related to the yield strength of the matrix material with which it is made of i.e. titanium. The strength of titanium powder compacts is 410 MPa. Considering that the matrix is reinforced with 10% TiO₂ and the strength of TiO₂ is about 600 MPa, the strength of the matrix (σ_d) using simplified rule of mixture is computed to be 420 MPa. Thus, the above relation can be rewritten as follows:

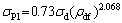                         (7)

The proportionality constant associated with Eq. (7) is in well agreement with the reported values for titanium foam [25] and aluminum foam or aluminum syntactic foam (Table 2).

3.4.2 Effect of relative density on modulus

The modulus of the samples is measured through sonic modulus dynamic elastic properties analyzer (DEPA) apparatus. Figure 10 shows the variation of elastic modulus as a function of relative density. Here, a large extent of variation is noted. This is primarily due to the same reason as mentioned in preceding section. It is observed that the elastic modulus increases with increase in relative density. In order to get the correlation of elastic modulus with relative density, the best fitted plots for power law relation and linear relation are considered.

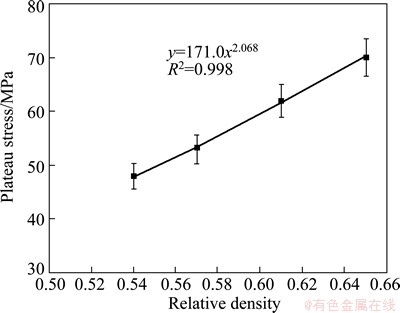
Fig. 9 Variation of plateau stress as a function of relative density

Table 2 Values of empirical constants reported in various references and obtained in this work

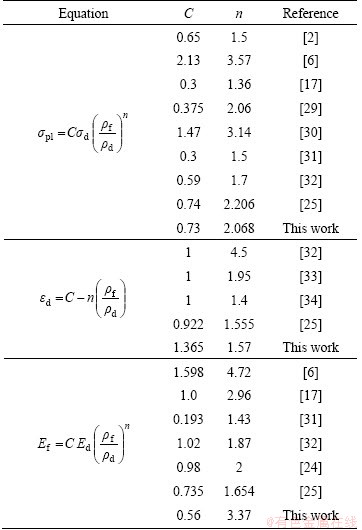
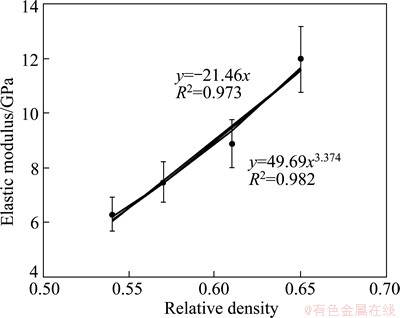
Fig. 10 Variation of elastic modulus as a function of relative density

The power law relation is the best fitted one. Power law also defines its practical significance as it signifies that, elastic modulus is 0 when relatice density is 0. But when relative density is 1, its elastic modulus is 49.6 MPa, much lower than that of titanium. This is attributed to the fact that foam samples and matrix also contain some porosity. Moreover, the state of deformation of the titanium network in foam is different from that of dense titanium foam. It is then correlated with the elastic modulus of titanium matrix (E_s) in titanium cenosphere foam. Because 10% titanium is oxidized, the elastic modulus of titanium network is 130 GPa. The equation to correlate elastic modulus of the foam (E_f) with the relative density is as follows:

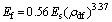                          (8)

The exponent and the proportionally constant are compared with reported values in Table 2. It is noted that these values are in the range of reported values and are in good agreement with those reported by the present investigators in the case of open cell titanium foam [25].

Fig. 11 Variation of densification strain as a function of relative density

3.4.3 Effect of relative density on densification strain

The densification strain (ε_D) as a function of relative density is shown in Fig. 11. It shows that ε_D decreases with increase of relative density. An attempt is made to find the best possible correlation between ε_D and relative density. It is well fitted for both linear and power law relations. Besides the two, the power law relation is fitted better than the linear one. The practically power law relation is insignificant. When relative density is 0, densification strain is infinity. This is not possible in the present domain of tests scenarios conducted. The value of ε_Dmax will be 1.0 at relative density of 1, where the linear relation as stated below explains its practical significance. When relative density is 0, the value of ε_D will be 1.0. However, here it is marginally higher. This isbecause that the densification strain is less than that of porosity. This is again due to the fact that even in the fully compacted condition, a reasonably good amount of porosity is noted. The value of ε_D in the cold compacted samples is in the range of 10% to 12%, less than the absolute porosity of the foam samples. The value of slope in Eq. (9) is also in good agreement with the reported value (Table 2). A very close value of this slope in the case of open cell titanium foam is examined as follows [25]:

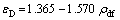                         (9)

3.4.4 Effect of relative density on energy absorption

The energy absorption (E_ab) of titanium foam is also computed from stress-strain curves. Energy absorption up to densification strain (ε_D) of all the titanium foam is calculated as follows:

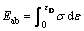                              (10)

where σ is the flow stress.

In this work, E_ab is calculated through digitization of the stress-strain curves with very small grid marking. A strain level of 0.4 is considered to compute the energy absorption. The energy absorption efficiency (η) is then calculated as follows [35,36]:

                              (11)

Figure 12 represents variation of E_ab as a function of relative density. Here two types of the best fit options are examined as

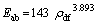                            (12)

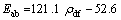                        (13)

The linear fit has better R² value than the power law fit. But the R² values in both the cases are near to 1.

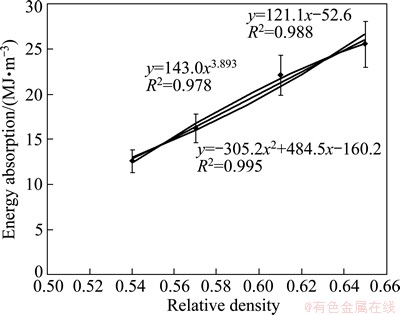
Fig. 12 Variation of energy absorption as a function of relative density

However, the linear relations states that, E_ab is -52.6 MJ/m³ when relative density is 0. This has no practical significance. In the case of power law fit, when relative density is 0, E_ab is 0. This means that gas/air/vacuum in open atmosphere will hardly absorb any energy as the σ_pl=0. It also signifies that the energy absorption increases with increase in relative density. If relative density is 1, the value of E_ab of titanium is 143 MJ/m³. This would be equal to energy absorbed by dense Ti-TiO₂ composite up to a strain level of 0.4.

The yield stress of dense Ti-TiO₂ composite is ~440 MPa. The energy absorption up to strain level of 0.4, considering no change in stress with strain up to strain of 0.4 and energy absorption efficiency of 0.8, comes to be 141 MJ/m³. The proportionality constant associated with the Eq. (12) is also 143 MJ/m³. If ultimate tensile strength of dense Ti-TiO₂ composite is consided, then the energy absorption will be much higher. The ultimate tensile strength of Ti-TiO₂ composite through rule of mixture can be calculated as 900 MPa. If the energy absorption efficiency is from 60% to 70% and there is no change in stress of the composite, the energy absorption of Ti-TiO₂ composite 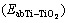will be from 216 to 252 MJ/m³. Because of these values of energy absorption of Ti-TiO₂ matrix, Eq. (12) can be rewritten as

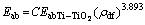                    (14)

where C is an empirical constant and E_abTi-TiO2 is the energy absorption by Ti-TiO₂ composite. C may be from 0.52 to 1.0. The value of C depends on the assumption used for calculation of E_abTi-TiO2. If an ultimate tensile strength criterion is considered, it will be low. But if yield strength is considered, it would be larger.

Figure 13 shows the variation of energy absorption efficiency (η) as a function of relative density. The η is minimum at lower relative density and at an intermediate relative density, η is maximum. In the case of lower relative density, flow stress (σ_f) decreases after linear region whereas in the case of the higher relative density, σ_f increases slowly with strain. But at intermediate relative density, σ_f remains almost flat with strain after initial linear period. This is due to the micro structural variation in these foams and change in deformation behavior. However, energy absorption efficiency of titanium cenosphere foams developed in the present investigation is more than 75%, is significantly higher than that of dense titanium or titanium alloys (50%-60%).

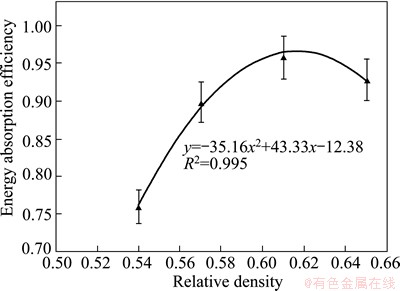
Fig. 13 Variation of energy absorption efficiency as a function of relative density

3.5 Performance index

The performance index of these titanium cenosphere syntactic foams is measured with respect to that of dense titanium. Two types of performance indexes (P_F1 and P_F2) are computed. These indices are defined as follows:

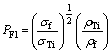                         (15)

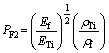                          (16)

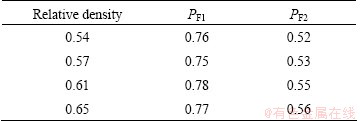
The values of P_F1 and P_F2 as functions of relative density are listed in Table 3. Table 3 shows that performance indexes of these titanium cenosphere syntactic foams are in the range of 0.52 to 0.78. These performance indexes are almost invariant to the relative density (within the present domain of relative density). However, at relatively high relative density, these foams showed marginally higher performance indexes. But considering all these values and the recommendation of SALIMON et al [2], these foams are good to replace dense titanium in engineering applications. Use of cenospheres as space holder would certainly make these foams to be cost-effective.

Table 3 Performance indexes of titanium cenosphere syntactic foam at varying relative density

4 Conclusions

1) Cenospheres of coarser size (150 mm) can be successfully used as space holder to make titanium cenosphere syntactic foam through powder metallurgy route. However, there is a need to optimize applied pressure during cold compaction. A fraction of cenospheres crushed and the extent of crushing are a strong function of applied load. As high as 30% cenospheres crushed at a cold compaction pressure of 75 MPa. Because of cenosphere crushing and its agglomeration, the cells in titanium cenosphere syntactic foams are not perfectly spherical.

2) The sintering temperature of 1100 °C and sintering time of 2 h are sufficient to get good sintered foams.

3) The stress-strain curves of these foams are similar to those of conventional foams. In the plateau region, the extent of stress oscillation is not detected. This is due to finer cells in the foam samples. At higher relative density, foams show marginal strain hardening effect. But if relative density is less than 0.61, no strain hardening is noticed.

4) The plateau stress, densification strain, modulus and energy absorption of this titanium cenosphere syntactic foams follow the standard relationships applicable for conventional foams. The constants related to these relationships are in good agreement with the reported values.

5) The performance indices calculated for these foams with respect to dense titanium and titanium alloys states that these foams are good to replace titanium in engineering applications.

References

[1] BANHART J. Manufacture, characterisation and application of cellular metals and metal foams [J]. Progress in Material Science, 2001, 46 (6): 559-632.

[2] SALIMON A, ASHBY M F, GREER A L. Potential applications for steel and titanium metal foam [J]. Journal of Material Science, 2005, 40: 5793-5799.

[3] GIBSON L J, ASHBY M F. Cellular solids, structure and properties [M]. London: Cambridge University Press, 1997.

[4] LI J P, LI S H, de GROOT K, LAYROLLE P. Preparation and characterization of porous titanium [J]. Key Engineering Material, 2002, 218-220: 51-54.

[5] KOTAN G, BOR . Production and characterization of high porosity Ti-6Al-4V foam by space holder technique in powder metallurgy [J]. Turkish Journal of Engineering and Environmental Sciences, 2007, 31: 149-156.

[6] ESEN Z, BOR . Processing of titanium foams using magnesium spacer particles [J]. Scripta Materialia, 2007, 56(5): 341-344.

[7] CHEN L J, LI T, LI Y M, HE H, HU Y H. Porous titanium implants fabricated by metal injection molding [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(5): 1174-1179.

[8] WANG Y Q, TAO J, ZHANG J L, WANG T. Effects of addition of NH₄HCO₃ on pore characteristics and compressive properties of porous Ti-10%Mg composites [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(5): 1074-1079.

[9] ZOU C M, LIU Y, YANG X, WANG H W, WEI Z J. Effect of sintering neck on compressive mechanical properties of porous titanium [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 485-490.

[10] XUE X B, WANG L Q, WANG M M,  W J, ZHANG D. Manufacturing, compressive behaviour and elastic modulus of Ti matrix syntactic foam fabricated by powder metallurgy [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(1): 188-192.

[11] DUNAND D C. Processing of titanium foams [J]. Advances in Engineering Material, 2004, 6(6): 369-376.

[12] IMWINKELRIED T. Mechanical properties of open-pore titanium foam [J]. Journal of Biomedical Materials Research Part A, 2007, 81(4): 964-970.

[13] LEFEBVRE L P, BARIL E. Effect of oxygen concentration and distribution on the compression properties on titanium foams [J]. Advanced Engineering Materials, 2008, 10(9): 868-876.

[14] WEN C E, YAMADA Y, SHIMOJIMA K, CHINO Y, ASAHINA T, MABUCHI M. Processing and mechanical properties of autogenous titanium implant materials [J]. Journal of Materials Science: Materials in Medicine, 2002, 13(4): 397-401.

[15] WEN C E, MABUCHI M, YAMADA Y, SHIMOJIMA K, CHINO Y, ASAHINA T. Processing of biocompatible porous Ti and Mg [J]. Scripta Materialia, 2001, 45(10): 1147-1153.

[16] LAPTEV A, VYAL O, BRAM M, BUCHKREMER H P, STOVER D. Green strength of powder compacts provided for production of highly porous titanium foam [J]. Powder Metallurgy, 2005, 48(4): 358-364.

[17] MANSOURIGHASRI A, MUHAMAD N, SULONG A B. Processing titanium foams using tapioca starch as a space holder [J]. Journal of Materials Processing Technology, 2012, 212(1): 83-89.

[18] BANSIDDHI A, DUNAND D C. Shape-memory NiTi foams produced by replication of NaCl space-holders [J]. Acta Biomaterialia, 2008, 4(6): 1996-2007.

[19]  Processing of porous TiNi alloys using magnesium as space holder [J]. Journal of Alloys and Compounds, 2009, 478(1-2): 705-710.

[20] BALCH D K, O’DWYER J G, DAVIS G R, CADY C M, GRAY G T, DUNAND D C. Plasticity and damage in aluminum syntactic foams deformed under dynamic and quasi-static conditions [J]. Materials Science and Engineering A, 2005, 391(1-2): 408-417.

[21] KISER M, HE M Y, ZOK F W. The mechanical response of ceramic microballoon reinforced aluminum matrix composites under compressive loading [J]. Acta Materialia, 1999, 47(9): 2685-2694.

[22] LUCKEY H A, KUBLI F. Titamium alloys in surgical implants [M]. Baltimore: ASTM International, 1983.

[23] MONDAL D P, DAS S, JHA N. Dry sliding wear behaviour of aluminum syntactic foam [J]. Materials Design, 2009, 30(7): 2563-2568.

[24] MONDAL D P, MAJUMDAR J D, JHA N, BADKUL A, DAS S, PATEL A, GUPTA G. Titanium-cenosphere syntactic foam made through powder metallurgy route [J]. Materials Design, 2012, 34: 82-89.

[25] JHA N, MONDAL D P, MAJUMDAR J D, BADKUL A, JHA A K, KHARE A K. Highly porous open cell Ti-foam using NaCl as temporary space holder through powder metallurgy route [J]. Material Design, 2013, 47: 810-819.

[26] MONDAL D P, KHEDLE R, BADKUL A, JHA N, DAS S. Aluminium syntactic foam through stir-casting technique using cenosphere as microballoons [J]. Indian Foundary Journal, 2012, 58(8): 31-38.

[27] WU G H, DOU Z Y, SUN D L, JIANG L T, DING B S, HE B F. Compression behaviors of cenosphere-pure aluminum syntactic foams [J]. Scripta Materialia, 2007, 56(3): 221-224.

[28] BALCH D K, DUNAND D C. Load partitioning in aluminum syntactic foams containing ceramic microspheres [J]. Acta Materialia, 2006, 54(6): 1501-1510.

[29] YU S, LIU J, WEI M, LUO Y, ZHU X, LIU Y. Compressive property and energy absorption characteristic of open-cell ZA22 foams [J]. Mater Design, 2009, 30: 87-90.

[30] MILTZ J, GRUENBAUM G. Evaluation of cushioning properties of plastic foams from compressive measurements [J]. Polym Eng Sci, 1981, 21: 1010-1014.

[31] CHRISTIAN G, OPPENHEIMER O S M, DUNAND D C. High strength, low stiffness, porous NiTi with superelastic properties [J]. Acta Biomaterialia, 2005, 1(6): 705-716.

[32] NIU W, BAI C, QIU G, WANG Q. Processing and properties of porous titanium using space holder technique [J]. Materials Science and Engineering A, 2009, 506(1-2): 148-151.

[33] ANDREWS A, SANDERS W, GIBSON L J. Compressive and tensile behaviour of aluminum foams [J]. Materials Science and Engineering A, 1999, 270(2): 113-124.

[34] SHEN J H, LU G X, DONG R A. Compressive behaviour of closed-cell aluminium foams at high strain rates [J]. Composite B, 2010, 41(8): 678-685.

[35] RAJENDRAN R, MOORTHI A, BASU S. Numerical simulation of drop weight impact behaviour of closed cell aluminium foam [J]. Materials Design, 2009, 30(8): 2823-2830.

[36] AKTAY L, M. Finite element and coupled finite element/smooth particle hydrodynamics modeling of the quasi-static crushing of empty and foam-filled single, bitubular and constraint hexagonal-and square-packed aluminum tubes [J]. Materials Design, 2008, 29(5): 952-962.

采用粗空心微球低压粉末冶金法制备空心微球复合泡沫钛

N. JHA¹, D. P. MONDAL¹, M. D. GOEL¹, J. D. MAJUMDAR², S. DAS¹, O. P. MODI¹

1. CSIR-Advanced Materials and Processes Research Institute, Council of Scientific and Industrial Research, Bhopal 462064, India;

2. Department of Metallurgical and Materials Engineering, Indian Institute of Technology, Kharagpur 721302, India

摘  要：在低压下采用粉末冶金法，使用粗尺寸空心微球制备出不同相对密度的钛空心微球复合泡沫材料。在压力为60～70 MPa，通过冷压制备得到不同相对密度的泡沫钛。研究冷压压力与空心微球破碎倾向和相对密度的函数关系。研究制备的泡沫钛材料的压缩变形行为，考虑到实际应用，建立了平台应力、弹性模量、致密化应变和能量吸收之间的经验关系。对比泡沫钛和致密钛的性能指标，发现在工程应用中泡沫钛是致密钛的优秀替代物。

关键词：泡沫钛；空心微球；相对密度；平台应力；能量吸收

(Edited by Chao WANG)

Corresponding author: D. P. MONDAL; E-mail: dpmondal@ampri.res.in

DOI: 10.1016/S1003-6326(14)63032-6