CSP辊底式均热炉钢坯氧化烧损的数值模拟

欧俭平^{1, 2}，赵迪¹，张兴华¹，吴青娇¹，王芳¹

(1. 中南大学 能源科学与工程学院，湖南 长沙，410083；

2. 中南大学 材料科学与工程博士后流动站，湖南 长沙，410083)

摘  要：基于数值模拟方法研究65Mn钢坯在均热过程中氧化层的动态增长过程。根据紧凑式带钢生产(CSP)均热工艺特点，利用等效热阻和等效质量法，以实验均热炉为研究对象，建立三维非稳态钢坯均热过程氧化烧损数学模型，考虑氧化层的增长对传热过程的影响对氧化烧损量进行计算。利用计算流体力学软件FLUENT 6.2计算65Mn钢坯均热过程中加热速度、均热温度及空气消耗系数对钢坯氧化烧损量的影响，首先计算符合工艺要求的稳定的初始温度场，然后耦合氧化烧损UDF程序，进行计算分析。研究结果表明：在加热过程中生成的氧化层增大了换热热阻，使钢坯的加热速度减小；钢坯氧化烧损量随加热速度的增大而减小；当达到同一特定的均热温度时，钢坯氧化烧损量随空气消耗系数的增大近似呈线性递增；当空气消耗系数一定时，钢坯氧化烧损量随均热温度的提高而急剧增加；数值计算结果与实验结果变化趋势一致，并在CSP均热温度范围内较吻合。

关键词：紧凑式带钢生产(CSP)；均热炉；氧化烧损；计算流体力学

中图分类号：TE963          文献标志码：A         文章编号：1672-7207(2010)02-0764-06

Numerical simulation on loss of iron scale in roller hearth soaking furnace of CSP line

OU Jian-ping^{1, 2}, ZHAO Di¹, ZHANG Xing-hua¹, WU Qing-jiao¹, WANG Fang¹

 (1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;

2. Postdoctoral Ambulatory Station of School of Material Science and Engineering, Central South University,
Changsha 410083, China)

Abstract: Based on the method of numerical simulation, the dynamic growth of oxide scale was studied in the soaking process of 65Mn slab. According to the technological characteristics of soaking furnace of CSP (Compact strip production) line, the 3D-unsteady mathematical model of the loss of iron scale in soaking process was established with the experimental reheating furnace as instance by utilizing the methods of equivalent thermal resistance and equivalent mass. The effect of thickening of iron oxidation on heat transfer between gas and slab was considered in the model of loss of iron scale. The influences of the rate of heating, the soaking temperature and the coefficient of air consumption over the loss of iron scale were studied by CFD (Computational fluid dynamics) software FLUENT 6.2 in the soaking process. Firstly, the steady origin temperature field was calculated, and then the UDF (User-defined functions) program of calculating the loss of iron scale was coupled in the calculating of numerical simulation. The results show that the rate of heating decreases due to the growth of oxidation layer in soaking process when the thermal resistance between gas and slab increases. The quantity of loss of iron scale increases with the increase of the coefficient of air consumption under the condition of certain soaking temperature. When the coefficient of air consumption is certain, the quantity of loss of iron scale increases with the increase of soaking temperature rapidly. The results of numerical simulation is consistent with experimental ones, and the error is very small within the range of soaking temperature in CSP line.

Key words: compact strip production (CSP); soaking furnace; loss of iron scale; computational fluid dynamics (CFD)

钢坯在加热过程中表面会被氧化，生成氧化铁皮，这不仅降低钢的性能，而且降低钢的成材率。近年来，铁矿石价格持续增长，这进一步促使钢铁企业成本增加。优化钢坯加热工艺、降低氧化烧损量，对钢铁企业降低成本、提高经济效益有重要意义。在加热炉内，钢坯的氧化过程是铁元素透过氧化层向外扩散，烟气中的氧化性气体透过氧化层向钢坯内部扩散并产生化学反应的结果。炉气内的氧化性气体主要为SO₂，O₂，CO₂和H₂O，根据氧化程度的不同，生成几种不同的铁的氧化物FeO，Fe₃O₄和Fe₂O₃^[1]。在高温环境下，钢坯具有多项氧化特性。Basabe等^[2]通过模拟热轧前的钢坯加热过程研究了在不同加热气氛、加热时间及加热温度下的氧化层成分，研究表明氧化层主要由FeO，Fe₂O₃及Fe₃O₄组成，各成分含量随加热条件的变化而变化。Chen等^[3-7]研究了钢坯在热轧过程中氧化层的微观表面形态及增长过程，其研究方法与结果为探讨钢坯在高温加热过程中的氧化行为提供了参考。曹杰等^[8]利用电炉研究不同钢种在空气介质下加热过程中的氧化行为，并测定氧化烧损量，实验结果表明：氧化烧损量随加热时间的延长而增大，不同钢种的氧化烧损量也不同。以上研究是在进行了多项简化甚至脱离了实际钢坯加热环境条件下进行的，而钢坯加热过程大多在火焰炉中完成，由于燃烧过程不稳定，高温烟气对钢坯的冲刷等产生不利影响，使钢坯的氧化过程呈现出新的特点。65Mn钢属于含碳量较高的碳素结构钢，该钢种是紧凑式带钢生产(Compact strip production, CSP)工艺新开发钢种之一^[9]。在此，本文作者根据CSP均热工艺特点，利用FLUENT软件耦合钢坯氧化烧损UDF程序研究65Mn钢坯的在实验均热炉中的均热过程，并研究氧化层动态增长对钢坯与炉气换热的影响。

1  数值模拟

1.1  数学模型

1.1.1  炉内传热控制方程组

根据实验均热炉内流体流动及传热特点，选用k-ε湍流模型、DO(Discrete ordinates)辐射模型和EDM (Eddy-dissipation model)燃烧模型模拟炉内气相的流动与传热，其主要控制方程组如下^[10-13]。

连续性方程：

动量方程：

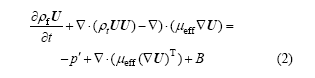
能量方程：

对于钢坯，导热方程为：

式中：ρ_f为气体密度；U为气体速度；p为压力；p′为修正的压力；B为体积力；H为总热焓；C_{p, f}为气体比热容；λ_f为气体导热率；μ_T为湍流黏性系数；μ_eff为气体的有效黏度；ρ_s，C_{p, s}和λ_s分别为金属材料的密度、比热容、导热率；T_s为金属热力学温度。

1.1.2  氧化烧损计算模型

在实际工业加热炉中，由钢坯运动而引起的震动使部分钢坯氧化层脱落，导致氧化层对钢坯失去保护作用，这将进一步加剧钢坯的氧化；与此同时，燃烧工况随生产节奏的变化而变化，即炉内热状况并不是稳定不变的，这使得钢坯的实际氧化物理过程十分复杂，导致建立钢坯在加热过程中的氧化烧损计算模型较困难；因此，需对其物理过程进行简化，然后，考虑实际因素对模型进行修正。

首先考虑实验炉燃烧工况稳定、有部分钢坯氧化层脱落情况下的钢坯氧化烧损情况。其氧化烧损量满足下列微分方程^[14]：

式中：w为钢坯氧化烧损量，kg/m²；w₀为初始氧化烧损量，kg/m²；t₀为钢坯开始加热时间，min；A₁和P₁为常数，0.5＜P₁＜1.0。

对式(5)两边同时积分，并利用式(6)，令A= (P₁+1)A₁，P=(P₁+1)^-1，可得：

在实际钢坯加热过程中，在实验炉内是动态升温过程，炉内气氛也不断变化，因此，需对式(7)进行修正。系数A和P的修正计算公式如下：

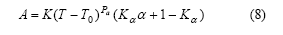
式中：T为钢坯温度，K；T₀为钢坯入炉温度，K；K和P_α为常数；K_α为平滑系数，0＜K_α＜1；K_P＞0。K，P_α，K_α，K_P和P_P均由实验数据回归得出，并且对于不同的钢种稍不同，取值分别为1.5×10^-15，5，0.60，0.75和0.015。

1.1.3  氧化层动态增长模型

由于氧化层的导热系数小于奥氏体钢的导热系数，在钢坯表面生成氧化层以后，钢坯的加热速度将明显变小。因此，在钢坯加热过程中，氧化烧损的数值模拟必须考虑氧化层的增长对传热过程的影响。氧化层大致分为3层，即FeO层、Fe₂O₃层和Fe₃O₄层，为了降低计算难度，不考虑各分界面的变化，而且在均热过程中，氧化层中的Fe₃O₄含量最大，故将氧化层简化为由Fe₃O₄单一成分组成^{[6, 15]}。氧化层的厚度可采用下式计算^[1]：

式中：s为氧化层厚度，mm；ρ为氧化层密度，取5 t/m³；w(Fe)为氧化层中铁的平均含量，取0.72。

为了降低计算难度，忽略氧化层实际增长过程对钢坯周围气体流动的影响。根据现场氧化铁皮厚度测试结果，在进行网格划分时，将氧化层的厚度在几何上假定为2 mm。同时，为揭示氧化层动态增长过程对钢坯加热过程的影响，利用等效热阻和等效质量法，将氧化层动态增长的过程转化为氧化层导热系数和密度动态变化的过程，其推导过程如下。

钢坯导热过程示意图如图1所示，钢坯从炉气中吸收的热量Q透过氧化层向钢坯基体传递，其中，由氧化层吸收热量Q_ox，透过氧化层传递给钢坯基体的热量Q_b=Q-Q_ox可由下式计算：

式中：A为钢坯表面积，m²；λ_ox为氧化层导热系数；ΔT为氧化层与钢坯基体间的温差，K。

图1  钢坯导热过程示意图

Fig.1  Schematic map of heat conduction of slab

事实上，在进行网格划分时，将氧化层厚度假定为δ_ox，即2 mm固定不变，为考虑氧化层对钢坯加热过程的影响，应用等效热阻法引入计算导热系数λ_ca，在计算程序中热阻以δ_ox/λ_ca形式出现。λ_ca为实际氧化层厚度的函数，其计算公式为：

同样，氧化层的增长将使氧化层的质量增大，应用等效质量法将氧化层厚度的增大过程转化为氧化层密度的动态增大过程，其计算式为：

1.2  研究对象与网格划分

研究对象为具有方形炉膛、原为测试自行设计燃气式燃烧器性能的实验均热炉。炉膛内部装有调节炉膛温度并起支撑钢坯试样作用的水平蛇形水管，在实验均热炉的2个平行侧面安装2个结构相似的燃烧器。为了减少网格划分和降低计算难度，忽略蛇形水管。钢坯的加热只需1个燃烧装置，故几何建模时只考虑1个燃烧器。如图2所示，在网格划分过程中对主要燃烧区、钢坯加热区及其表面氧化层进行网格加密。

图2  实验均热炉网格划分

Fig.2  Grid of experimental furnace

1.3  边界条件与计算工况

参照CSP均热工艺特点和实验均热炉的实验结果设置燃料流量及空气预热温度，使炉温达到工艺要  求^[16]。所用燃料为石油液化气，其低位发热量为 93.793 3 MJ/m³，氧化层的初始氧化烧损量为1 kg/m²。

钢坯固体表面采用壁面边界条件，发射率为0.8。钢种为65Mn，其热物性参数由经验公式计算得     到^{[1, 17]}，其导热系数和比热容拟合计算公式如下。

(1) 65Mn钢导热系数λ：

当273≤T-273＜1 173 K时，

λ=40.112-0.013 5(T-273)-2.333×10^-6(T-273)²

当1 173≤T-273≤1 523 K时，

λ=46.805-0.046 3(T-273)+2.644×10^-5(T-273)²

(2) 65Mn钢比热容C_p：

当273≤T＜1 173 K时，

C_p=-471.138+0.027 8(T-273)+2.477×10^-4(T-273)²

当1 173≤T≤1 523 K时，

C_p=-859.129-0.342(T-273)+1.676×10^-4(T-273)²

采用标准壁面函数法，对近壁面流场速度的计算进行近似处理；实验均热炉墙内衬有优质耐火材料，其散热可以忽略，为绝热边界条件。

在计算过程中，首先按照稳态进行计算，将炉温稳定，并达到工艺要求，然后，嵌入氧化烧损UDF程序进行非稳态计算。为了减少计算时间，湍流模型每计算10步耦合1次辐射传热；速度压力场计算采用SIMPLEC法修正；控制方程采用二阶迎风格式离散。

计算工况：首先计算2组在相同炉温下，不存在钢坯氧化和存在钢坯氧化情况时的升温过程，以揭示钢坯表面的氧化层钢坯对加热速度的影响。钢坯氧化特性工况考虑温升率、均热温度、空气消耗系数、保温时间4个因素，具体计算工况如表1所示，其中：入炉温度均为1 073 K，均热保温时间为20 min。

表1  计算工况

Table 1  Computational cases

2  结果与分析

在钢坯加热过程中，由于存在钢坯表面氧化层，增大了钢坯与炉气间的换热热阻。氧化层对钢坯加热过程的影响如图3所示，可见：在钢坯入炉温度为    1 073 K、要求加热到相同炉温的条件下，不存在钢坯氧化过程时的钢坯平均温度与存在氧化过程时的平均温度之差(?T)随加热时间的延长近似呈递增趋势；根据表1，对于整个加热过程的平均温升率，前者为41.07 K/min，后者为39.81 K/min。可见：氧化层的存在增大了钢坯的导热热阻。

图3  氧化层对钢坯加热过程的影响

Fig.3  Influence of oxide scale on reheated process of slab

2.1  加热速度对氧化烧损量的影响

加热速度对氧化烧损量的影响见图4。可见：当入炉温度为1 073 K，以不同的加热速度加热到1 473 K，并保温20 min后，钢坯的氧化烧损量随加热速度的升高而减小。这主要是因为加热速度的增大使得钢坯在高温烟气中的时间减少；在保温时间不变时，总在炉时间减少。在CSP工艺中，承担均热功能的辊底式均热炉衔接生产节奏并不相同的连铸机和连轧机。实际上，辊底式均热炉的加热段和均热段的划分并不是固定的，而是根据钢坯温度是否达到指定温度不断变化，因而当钢坯以较少的时间达到均热温度而快速进入均热保温时，意味着辊底炉有更多的均热缓冲时间。

2.2  均热温度对氧化烧损量的影响

均热温度对氧化烧损量的影响如图5所示。可见：当入炉温度为1 073 K，以38.51 K/min加热速度分别加热到1 273，1 323，1 373，1 423和1 473 K，并保温20 min时，钢坯的氧化烧损量随均热温度的增高而迅速增加；当均热温度为1 273 K时，钢坯的氧化烧损量仅为1.396 kg/m²；而在1 473 K时，钢坯的氧化烧损量增加到7.2 kg/m²。事实上，钢坯的氧化过程是铁元素透过氧化层向外扩散，烟气中的氧化性气体元素透过氧化层向钢坯内部扩散并产生化学反应的过程。当钢坯表面的温度增高时，铁元素与氧化性气体元素的扩散性将增强，从而使氧化层的厚度急剧增加。

入炉温度为1 073 K

图4  氧化烧损量与加热速度的关系

Fig.4  Relationship between quantity of loss of iron scale and rates of heating

入炉温度为1 073 K，升温速度为38.51 K/min

图5  氧化烧损量与均热温度的关系

Fig.5  Relationship between quantity of loss of iron scale and soaking temperature

2.3  空气消耗系数对氧化烧损量的影响

空气消耗系数对氧化烧损量的影响如图6所示。可见：当入炉温度T₀为1 073 K，以38.51 K/min加热速度到1 473 K，并在空气消耗系数分别为1.0，1.1，1.2和1.3的气氛中保温20 min，钢坯的氧化烧损量随空气消耗系数的增加近似呈线性增加。这主要是因为在实际燃烧工况的调节过程中，采用较大的空气消耗系数时，未参与燃料燃烧的助燃风增多，均热炉内含有大量的残留氧气，加剧了钢坯的氧化。因此，在满足燃料燃烧充分的前提下，应使用较小的空气消耗系数，减小炉内氧化性气体成分。

入炉温度为1 073 K，升温速度为38.51 K/min

图6  氧化烧损量与空气消耗系数的关系

Fig.6  Relationship between quantity of loss of iron scale and coefficient of air consumption

3  模型的验证

为了验证所建氧化烧损模型的适用性，根据文献[8]中钢坯氧化烧损实验工况进行数值模拟，即以    1 173 K为入炉温度和固定升温速度加热到1 273，   1 323，1 373，1 423和1 473 K，并保温20 min，数值计算与实验结果如图7所示。可见：氧化烧损量均随

1—数值计算结果；2—实验结果

图7  不同均热温度时氧化烧损量数值计算与
实验结果对比

Fig.7  Comparison results of numerical simulation with experimental results at different soaking temperatures

加热温度的升高而升高，变化趋势一致；当加热温度为1 273，1 423和1 473 K时，数值计算结果和实验结果基本吻合，但烧损量的数值计算结果在1 323和   1 373 K时明显比实验值偏大。其主要原因是：钢坯加热氧化烧损数学模型是基于多项假设前提下建立的，各系数的选取存在一定的主观性；而实验条件是在空气介质气氛下加热，导致数值计算时所设定的条件不能完全逼近实验条件。但注意到在CSP均热工艺中，钢坯的均热温度多在1 373 K以上，故数值计算结果在该温度范围内与实验结果较吻合。

4  结论

(1) 钢坯在加热过程中表面生成的氧化层增大了换热过程中的导热热阻，减小了钢坯的升温速度，在一定程度上增大了总在炉时间。

(2) 氧化烧损量随升温速度的增大而减小。加热速度的增大减小了钢坯在高温烟气中的时间，并使钢坯的总在炉时间减小。在CSP工艺中，应增大加热速度，以减少钢坯的氧化烧损量。

(3) 氧化烧损量随均热温度的增大而迅速增加：当均热温度为1 273 K时，钢坯的氧化烧损量为1.396 kg/m²，而在1 473 K时，氧化烧损量急剧增加到7.230 kg/m²。因此，在满足轧制工艺的条件下，应尽可能减小均热温度。

(4) 氧化烧损量随空气消耗系数的增加近似呈线性增加，在满足燃料燃烧充分的前提下，应使用较小的空气消耗系数，以减小炉内氧化性气体成分。

参考文献：

[1] 蔡乔方. 加热炉[M]. 北京: 冶金工业出版社, 1982: 149-158.
CAI Qiao-fang. Reheating furnace[M]. Beijing: Metallurgy Industry Press, 1982: 149-158.

[2] Basabe V V, Szpunar J A. Phase composition of oxide scales during reheating in hot rolling of low carbon steel[J]. Steel Research International, 2006, 77(11): 818-824.

[3] Chen W C, Samarasekera I V, Kumar A, et al. Mathematical modelling of heat flow and deformation during rough rolling[J]. Ironmaking and Steelmaking, 1993, 20(3): 113-125.

[4] SUN W H, TIEU A K, Jiang Z Y, et al. Oxide scales growth of low-carbon steel at high temperatures[J]. Journal of Materials Processing Technology, 2004, 155/156(1/3): 1300-1306.

[5] SUN W H, TIEU A K, JIANG Z Y, et al. Surface characteristics of oxide scale in hot strip rolling[J]. Journal of Materials Processing Technology, 2003, 140(1/3): 76-83.

[6] Torrees M, Colas R. A Model for heat conduction through the oxide layer of steel during hot rolling[J]. Journal of Materials Processing Technology, 2000, 105(3): 258-263.

[7] Tang J, Tieu A K, Jiang Z Y. Modelling of oxide scale surface roughness in hot metal forming[J]. Journal of Materials Processing Technology, 2006, 177(1/3): 126-129.

[8] 曹杰, 项长祥, 陈冬, 等. 几种高速钢的氧化脱碳行为[J]. 北京科技大学学报, 2000, 22(1): 16-30.
CAO Jie, XIANG Chang-xiang, CHEN Dong, et al. Oxidation and decarbonisation behavior of several high speed steels[J]. Journal of University of Science and Technology Beijing, 2000, 22(1): 16-30.

[9] 傅杰. 新一代低碳钢: HSLC钢[J]. 中国有色金属学报, 2004, 14(S1): 82-90.
FU jie. New generation low carbon steel: HSLC steel[J]. The Chinese Journal of Nonferrous Metal, 2004, 14(S1): 82-90.

[10] 范维澄, 万跃鹏. 流动及燃烧的模型与计算[M]. 合肥: 中国科技大学出版社, 1992: 33-35.
FAN Wei-cheng, WAN Yue-peng. Modellings and computations of fluid flow and combustion[M]. Hefei: University of Science and Technology of China Press, 1992: 33-35.

[11] 赵坚行. 燃烧的数值模拟[M]. 北京: 科学出版社, 2002: 98-118.
ZHAO Jian-xing. Numerical simulation of combustion[M]. Beijing: Science Press, 2002: 98-118.

[12] OU Jian-ping, MA Ai-chun, ZHAN Shu-hua, et al. Dynamic simulation on effect of flame arrangement on thermal process of regenerative reheating furnace[J]. Journal of Central South University of Technology, 2007, 14(2): 243-247.

[13] 肖泽强, 朱苗勇. 冶金过程数学数值模拟分析技术的应用[M]. 北京: 冶金工业出版社, 2006: 18-21.
XIAO Ze-qiang, ZHU Miao-yong. Applications of numerical simulation for analysis of metallurgical process[M]. Beijing: Metallurgy Industry Press, 2006: 18-21.

[14] 张正言. 宝钢热轧加热炉氧化烧损计算模型的建立和实施[J]. 宝钢技术, 2003(4): 30-32.
ZHANG Zheng-yan. Establishment and implementation of mathematical model for ignition loss in Bao Steel reheating furnace[J]. Bao Steel Technology, 2003(4): 30-32.

[15] Jiro T, Kin-Ya W, Toshimichi M, et al. Manufacture of wire rods with good descaling property[J]. Trans Iron Steel INST, 1982, 22(8): 646-656.

[16] 欧俭平, 吴慧卿, 肖佩林, 等. 新型燃气燃烧器性能试验研究[J]. 金属热处理, 2007, 32(10): 85-87.
OU Jian-ping, WU Hui-qing, XIAO Pei-lin, et al. Experimental study on the performance of a new type gas fired burner[J]. Heat Treatment of Metals, 2007, 32(10): 85-87.

[17] 陈家祥. 连续铸钢手册[M]. 北京: 冶金工业出版社, 1991: 254.
CHEN Jia-xiang. Manual book of continuous cast steel[M]. Beijing: Metallurgy Industry Press, 1991: 254.

收稿日期：2009-01-11；修回日期：2009-03-28

基金项目：湖南省博士后科学基金资助项目(2008RS4036)

通信作者：欧俭平(1970-)，男，湖南邵阳人，博士，副教授，从事高效传热、燃烧新技术及热工设备仿真与优化研究；电话：0731-88879863；      E-mail: oujp@mail.csu.edu.cn

(编辑 陈灿华)