基于克隆选择的小世界优化算法

陈乃建¹，张进华²，王孙安²，艾长胜¹

(1. 济南大学 机械工程学院，山东 济南，250022；

2. 西安交通大学 机械工程学院，陕西 西安，710049)

摘要：针对小世界算法在多极值等复杂函数优化中存在算法后期种群多样性退化、全局搜索效率下降等问题，提出一种基于种群克隆选择的小世界优化算法。该算法以小世界现象信息传递的高效性改进克隆过程中体细胞高频变异的随机性，实现克隆增殖、克隆选择以及小世界网络短连接等算子在局部空间的搜索，克隆删除与小世界随机长连接在全局空间的搜索。实验结果表明：各种克隆算子与小世界变异算子相结合，增加了种群的多样性，扩大了搜索范围。与其他算法相比，该算法在收敛速度和多极值点函数搜索能力等方面具有明显改善。

关键词：克隆选择；小世界；函数优化；变异

中图分类号：TP18，O224          文献标志码：A         文章编号：1672-7207(2012)08-3091-08

Small-world optimal algorithm based on clone selection

CHEN Nai-jian¹, ZHANG Jin-hua², WANG Sun-an², AI Chang-sheng¹

(1. School of Mechanical Engineering, University of Jinan, Jinan 250022, China;

2. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Abstract: To avoid trapping into degradation in diversity of population latterly and improve global searching efficiency in multi-extreme function optimization, a small-world optimal algorithm based on clone selection was proposed. Small world phenomena, known for high-efficiency of information flowing, were introduced to change in the randomness of somatic cell mutation. The clone proliferation, clone selection and small-world clustering were used to achieve the local searching; the clone deletion and small-world long-range shortcuts operators were combined to enhance the capability in global searching. The simulation results show that the combination of clone operators and small-world mutation operators can improve the diversity in population and expand the scope of search. Compared with other small-world algorithms, the proposed algorithm has remarkably improved the converging rate and the search ability in multi-extreme functions.

Key words: clone selection; small-world; function optimization; mutation

Milgram^[1]根据20世纪60年代所做的实验，证明美国社交网络中存在最短路径，即六度分离现象，并提出了小世界网络，而Watts等^[2-3]根据小世界网络的特征，创建了WS小世界模型，由此引起了人们对于复杂网络的研究热潮。在计算机路由、城市路网、病毒传播、传染模型等方面的成果表明，小世界网络中的局部短连接与随机长连接的结合是一种信息传递的高效方式。自杜海峰等^[4]将小世界现象用于函数优化以来，陈煜聪等^[5-6]分别针对该算法中存在的停滞现象、收敛性、局部短连接的搜索效率及种群多样性等方面存在的问题以跟踪替代、混沌扰动方式进行了优化，在一定范围内提高了算法性能，但仍存在多极值函数优化中易于陷入局部极值及进化过程中种群多样性退化等问题。克隆选择学说是生物免疫系统理论的重要学说^[7-8]，免疫学认为，亲和度的成熟和抗体多样性的产生主要是依靠抗体的高频变异，而非交叉或重组，因此克隆选择算法中更强调变异的作用，然而人工免疫算法中的变异多以个体随机遍历为特征，不利于算法收敛。为此，本文作者提出了基于克隆选择的小世界优化算法(Small-world optimization algorithm based on clone selection, SOABCS)，以小世界信息传递的高效性改进克隆选择中变异的随机性，在克隆增殖及克隆选择基础上以小世界网络短连接操作实现局部空间搜索，利用克隆删除与小世界长连接来促进对全局空间的搜索。通过对标准测试函数的仿真试验，证明了该算法的有效性、可行性。

1  克隆选择、小世界优化模型及定义

小世界网络通常是指既具有较短的平均路径长度又具有较高聚类系数的网络，即网络中两节点间的平均距离L随着网络节点数目N成对数增长：。因此，一般认为小世界现象有2个特点：一个是“聚类性”，即低维空间中短连接的有效性^[9]，另一个特点是“小世界效应”，即任意2个人最多可以通过6个熟人建立起联系—六度分离现象^[10]，这是一种随机信息传递过程的高效性、捷径性。因此，小世界网络利用小世界效应的随机长连接与局部聚类连接的有效组合，表现出极强的搜索效率。

免疫学认为，只有与抗原完全匹配或部分匹配、具备较高亲和力的B细胞，才能被免疫系统选中并进行克隆复制产生大量的后代，后代再通过体细胞高频变异、受体编辑等过程实现亲和力的成熟。而与抗原亲和力低的B细胞，将无法获得克隆的机会，即克隆选择和扩增。如果B细胞经过体细胞高频变异和受体编辑后出现退化，亲和力降低，则将被克隆删除。免疫系统中每天都有大量的抗体产生，不断更新抗体群，但只有少数亲和力高的抗体得以发展，大部分新增抗体凋亡了。这种抗体补充机制提高了免疫系统的抗原识别概率。亲和力成熟后的抗体在完成对抗原的消灭之后，克隆规模将受到抑制，极少数高亲和力的抗体转化为记忆细胞，当免疫系统受到相同或类似的抗原入侵时将再次被激活，如此周而复始，使生物系统具备高的自适应性^[11]。

本文将社会学领域的WS模型与克隆免疫学说相结合，优势互补，在克隆选择、发展亲和力高的抗体基础上，改进体细胞高频变异与受体编辑的随机性，以小世界现象特有的局部聚类特征与小世界效应有效组合信息传递的高效性、捷径性，实现种群的多样性及算法的快速收敛。

不失一般性，以X={x₁，x₂，…，x_m}为变量的优化问题：P=max{f(e^-1(A))：A?I}，其中，具有有限长度的字符串A=a₁a₂…a_l是变量X的抗体编码，记为A=e(X)；而X称为抗体A的解码，记为X=e^-1(A)；集I称为抗体空间，f为I上的实值函数，称为抗体—抗原亲和度函数。在抗体A中，a_i为等位基因，其取值与编码方式有关，一般将抗体位串分为m段，每段长为l_i，，每段分别表示变量x_i?[d_i，u_i]，i=1，2，…，m。对于二进制代码采用如下的译码方式：

           (1)

抗体种群空间为：

Iⁿ={A:A=[A₁A₂…A_n]，A_k?I，1≤k≤n}

正整数n为抗体种群规模，抗体群A=[A₁A₂…A_n]为抗体A的n元组，是抗体种群空间Iⁿ的一个点。则全局最优解集为：B^*?{A?I:f(A)=f^*?max(f(A'):A'?I)}。

抗体A_i的λ邻域集定义为：

     (2)

并记|ξ^λ(A_i)|为ξ^λ(A_i)的元素数目，|·|表示Hamming距离，一般λ很小。而抗体λ非邻域集定义为：

     (3)

抗体种群在基于克隆选择的小世界优化算法(SOABCS)的作用下，其种群演化过程可描述为：

      (4)

SOABCS主要操作过程如图1所示。而基于克隆选择的小世界优化模型如图2所示。

在抗体进化过程中，由于其抗体-抗原亲和度的大小不同，每个抗体获得克隆的规模不尽相同。抗体A由于亲和力大，获得较多的克隆机会，抗体B次之，而抗体C由于在进化过程中亲和力下降，而没有获得克隆机会，甚至可能在下一代进化中被免疫系统克隆删除，以抗体A或B的局部增殖替代，从而使抗体A和B同时在各自邻域内、外分别获得较多的小世界变异进化机会，将优化信息向离目标点最近的节点传递，从而有利于保持种群的多样性及算法的快速收敛。

图1  基于克隆选择的小世界优化算法的主要操作过程

Fig.1  Main operation process of SOABCS

图2  基于克隆选择的小世界优化模型

Fig.2  Small world optimal model based on clone selection

2  SOABCS操作算子与算法

2.1  主要操作算子

根据SOABCS的操作过程，主要操作算子定义如下：

定义1  克隆删除T_d^c 指在抗体群中以少数较优抗体代替因较低的抗体-抗原亲和度或与其他抗体具有相同的表现型，降低了种群多样性而被免疫系统删除的过程，是亲和度高的抗体局部增殖。对A={A₁， A₂，…，A_n}克隆删除操作可表示为：

B(k)=T_d^c(A(k))={T_d^c(A₁(k))，…，T_d^cA_n(k))}=

{b₁A₁，b₂A₂，…，b_nA_n}          (5)

由于克隆删除过程中删除抗体与增殖抗体在整个抗体群中只占少数，因此取：β₁+β₂+…+β_n=n，以保持算法的可持续性。

定义2  克隆增殖T_c^c 指通过无性繁殖(如细胞有丝分裂)可连续传代并形成群体。即：

C(k)=T_c^c(B(k))=[T_c^c(B₁(k)),…，T_c^c(B_n(k))]^T   (6)

其中，C_i(k)=T_c^c(B_i(k))=I_iB_i(k)，i=1，2，…，n，I_i为元素为1的q_i维行向量，即抗体B_i的q_i克隆。一般取

，

i=1，2，…，n              (7)

N_c > n是与克隆规模有关的设定值；Int(?)为上取整函数。克隆过后，种群变为：C(k)={C₁(k)，C₂(k)，…，C_n(k)}。其中：C_i(k)=[C_ij(k)]=[B_i1(k)，B_i2(k)，…，B_in(k)]，C_ij(k)=B_ij(k)=B_j(k)，j=1，2，…，q_i。

定义3  小世界短连接T_sc^c就是根据目标函数f(?)，将解空间中的一个点，即克隆增殖q_i个抗体，C_ij(k)=B_ij(k)=B_j(k)，j=1，2，…，q_i，C_i(k)?C(k)，在其邻域ξ^λ(C_i)内产生新抗体D_i(k)?D(k)，将信息从C_i(k)传递给ξ^λ(C_i)内与目标最靠近的节点D_i(k)，且λ比较小。即：

D(k)=T_sc^c(C(k))=[T_sc^c(C₁(k))，…，T_sc^c(C_n(k))] ^T  (8)

其中：T_sc^c (C_i(k))=C_i◎{q_c1^λ，q_c2^λ，…，q_cm^λ}。q_cm^λ={1,0}ⁿ为与C_i维数相同的列向量，其元素值为1的数量|q_cm^λ| ≤λ，以保证D_i在C_i邻域内，◎表示矩阵元素的“异或”位运算，即判断C_i与q_cm^λ的两个相应位元素的值是否相同，值不同时取真(1)，值相同时为假(0)。因此短连接后，抗体种群为：D(k)={A(k)，D₁(k)，D₂(k)，…，D_n(k)}，D_i(k)=A_i'={A_i1'，A_i2'，…，A_iqi'}。

定义4  小世界长连接T_se^c则是在D_i(k)的非邻域中按预先设定的概率q_si选择一点，生成抗体E_i(k)?E(k)：

E(k)=T_se^c(D(k))=

[T_se^c(D₁(k))，T_se^c(D₂(k))，…，T_se^c(D_n(k))]^T   (9)

2种方法实现小世界长连接^[12]：

(1) 与短连接类似，取T_se^c(D_i(k))=D_i◎{q_s1^λ，q_s2^λ，…，q_sm^λ}。q_sm^λ={1,0}ⁿ为与D_i 维数相同的列向量，其元素值为1的数量|q_sm^λ|＞λ，以保证E_i不在D_i的邻域内。因此D_i(k)?E_i(k)转移概率为：

      (10)

|q_sm^λ|表示随机矩阵元素值为1的数量，也表示抗体变化前后的Hamming距离。l为个体长度。

(2) 采用抗体逆转算子，即单个抗体按照一定的逆转概率，随机选取抗体中的2点，将这2点之间的基因段首尾倒转过来形成新的抗体。

以上2种小世界长连接实现方法在算法过程中交替使用。长连接变异后，抗体种群为：E(k)={A(k)，E₁(k)，E₂(k)，…，E_n(k)}，其中，E_i(k)={A_i′，A_i″}={A_i1′，…，A_ij′, A_ij+1″，…，A_iqi″}。

小世界短连接T_sc^c与随机长连接T_se^c一起构成了小世界变异算子。

定义5  克隆选择操作T_s^c 克隆选择操作是从抗体各自克隆增殖、小世界短连接、长连接变异后的子代中选择优秀的个体，产生新的抗体群。对于抗体群E(k)={A(k)，E₁(k)，…，E_n(k) }，则克隆选择为：

A(k+1)=T_s^c(E(k))=max{E_i(k)}=

{E_ij(k)|max f(e^-1(E_ij))，j=1，2，…，q_i}    (11)

可见，克隆选择操作是克隆增殖操作的逆操作。同一个抗体A_i经过克隆增殖后形成的亚群体经过小世界短连接、长连接变异后通过克隆选择实现局部亲和度升高。

2.2  算法

基于克隆选择的小世界优化算法基本步骤为：

步骤1  初始化抗体群规模N，算法最大迭代次数K_max，q_si，λ，k=0；

步骤2  抗体群初始化：A(0)={A₁(0)，A₂(0)，…，A_N(0)}?I^N；

步骤3  计算初始种群的亲和度：

A(0): {f(e^-1(A₁(0)))，…，f(e^-1(A_N(0)))}；

步骤4  判断循环结束条件是否满足：k=K_max或|f(e^-1(A^*))-f ^*|≤ε；其中A^*为最佳抗体，f ^*为目标函数最优值。满足结束，输出最优抗体；不满足继续；

步骤5  克隆删除：B(k)=T_d^c(A(k))={T_d^c(A₁(k))，T_d^c(A₂(k))，…，T_d^c(A_n(k))}={β₁A₁，β₂A₂，…，β_nA_n}；

步骤6  克隆增殖：C(k)=T_c^c(B(k))=[T_c^c(B₁(k))，T_c^c(B₂(k))，…，T_c^c(B_n(k))]^T；

步骤7  小世界变异算子：

(1) 小世界短连接算子：

D(k)=T_sc^c(C(k))=[T_sc^c(C₁(k))，…，T_sc^c(C_n(k))]^T；

(2) 小世界长连接算子：

E(k)=T_se^c(D(k))=[T_se^c(D₁(k))，…，T_se^c(D_n(k))] ^T；

步骤8  克隆选择：

A(k+1)=T_s^c(E(k))=max{E_i(k)}=

{E_ij(k)|maxf(e^-1(E_ij))，j=1，2，…，q_i}；

步骤9  执行k=k+1；返回步骤4。

2.3  算法复杂度分析

给定抗体群规模N，编码长度n，小世界聚类及长连接数量g，最大迭代次数为K_max，则空间复杂度为O(Ngn)，根据基于小世界网络模型的信息传递的时间上限^[13]αlg(N)²，在一次迭代中算法的时间复杂度最差为O((Ng)²αlg(N)²)，整个算法的时间复杂度为O(Q(Ng)²αlg(N)²)。

3  算法收敛性

基于克隆选择的小世界优化算法在局部搜索能力和搜索精度上优于小世界算法，可以克服种群多样性退化的缺点，其收敛性也能得到保证。

定理1  基于克隆选择的小世界优化算法所产生的种群序列是时齐的Markov链^[14]。

证明  在编码方式确定后，SOABCS种群是从一个状态A(k)={A₁(k)，A₂(k)，…，A_n(k)}到A(k+1)= {A₁(k+1)，…，A_n(k+1)}的有记忆随机游动，即

(12)

其中：T_d^c，T_c^c，T_sc^c，T_se^c，T_s^c分别表示算法中的克隆删除、克隆增殖、小世界短连接、长连接和克隆选择算子，均与k无关，因此，A(k+1)仅与A(k)有关，即随机过程{A(k)|k=1，2，…}是时齐的Markov链。证毕。

定理2  基于克隆选择的小世界优化算法以概率1收敛于全局最优解。

证明  设A_i={A₁ⁱ，A₂ⁱ，…，A_nⁱ }∈S，记为f(A_i)={f(A₁ⁱ)，f(A₂ⁱ)，…，f(A_nⁱ) }，若对于任意的A_j={A₁^j，A₂^j，…，A_n^j }∈S满足f(A_nⁱ)≥f(A_n^j)，k=1，2，…，n，则称为A_i≥A_j。此外，记C={A_i|A_i≥A_j，"A_j∈S}，若A_i∈C，则有：

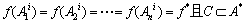  (13)

对于状态A_i，A_j∈S转移概率：

   (14)

式中，P{A_k^j|A_kⁱ}与局部聚类、小世界效应算子等有关，表示A_kⁱ转变为A_k^j的概率；， ，，分别为克隆删除、克隆增殖、小世界短连接、克隆选择概率。为个体发生小世界长连接的概率。

对于给定P=P_{Ai, Aj}(k)，如果A_i可达A_j，A_j可达A_i，则称为A_i和A_j互通，即A_i?A_j。根据互通关系的可传递性，把含A_i的等价类记作C(A_i):C(A_i)={A_i}?{A_i?A_j: A_i和A_j互通}，种群序列{A(k)，k≥0}是有限时齐的Markov链，根据SOABCS抗体的编码方式，对于一切A_i ，A_j?I，存在正整数k，使得，根据马氏链中遍历性判定定理，马氏链{A(k)，k≥0}是遍历的，且极限分布为满足平稳分布条件的唯一  解^[15]。由遍历性可知，马氏链的k步转移概率的极   限为

 (15)

由于遍历马氏链{A(k)，k≥0}具有平稳分布特征，满足≥0且。因此有

  (16)

又由于，所以

               (17)

故基于克隆选择的小世界优化算法是概率1收敛的。

4  仿真实验

为了验证算法的函数优化性能，分别从迭代次数、多极值函数优化以及参数影响等方面进行实验。

4.1  迭代次数测试

选取文献[4]中6个测试函数进行优化计算，即Rosenbrock函数f₁，Schaffer函数f₂，Shubert函数f₃，Needle-in-a-haystack函数f₄，Branin函数f₅，Griewank函数f₆。其测试结果与TSWA^[5]和CSWA^[6]进行比较。每种函数测试50次，采用与TSWA，CSW相同的参数：种群规模N=20，K_max为1 000，λ为1，q_si为0.8。

由表1可知，TSWA算法由于采用了跟踪替代方法优化，算法后期存在陷入局部极值问题，虽然除函数f₁外，每次都能得到最优解，但其仅依靠算法局部极值点停留次数来实现全局寻优，因此其迭代次数是非常大的。CSWA利用混沌扰动方式对小世界算法进行改进，算法收敛性比TSWA有了很大提高，但由于混沌扰动方式只是一种局部搜索方法，对于多极值问题算法收敛速度下降。而SOABCS算法在求解f₃，f₅函数时在最大代数，平均代数及代数标准差等方面与TSWA相比有较大优势，与CSWA相比虽有所改善，但相差不大，甚至CSWA在f₅函数的平均代数略优于SOABCS，但对于多极值的f₂，f₄及f₆函数，SOABCS在最大代数、平均代数及代数标准差等方面性能比TSWA及CSWA都有了较大提高。主要是由于SOABCS算法能够在候选解附近，根据亲和度产生变异解的群体，并且将抗体群落在可行解的范围内，能够扩大搜索范围，增强种群的多样性，因而其搜索效果整体上优于TSWA及CSWA。

4.2  多极值点函数测试

为验证SOABCS算法的种群多样性及其全局多极值点搜索能力，采用以下函数进行验证：

表1  TSWA，CSWA与SOABCS函数优化测试结果

Table 1  Experimental result of test functions in TSWA, CSWA and SOABCS

Hansen函数：

该函数共有760个局部极小值，全局最小值为-176.541 793，分别在9个点处取值。

Bohachevsky函数：

全局最小值为-0.24，分布在(-0.24，0)和(0，0.24)范围内。

多峰函数：

该函数有4个全局最大值，32个局部最优解，尤其是在中间区域有一个取值与全局最大值很接近的局部最大值凸台。

SOABCS算法对以上3个函数全局极值点搜索结果与CSWA进行对比测试，SOABCS算法某次寻优解分布情况如图3所示。图4所示为SOABCS与CSWA搜索代数与全局极值点数量对比。其中设定最大迭代K_max为250，种群规模N为50，CSWA算法中混沌扰动个体数量为5，SOABCS克隆规模为N。其他参数选取与迭代次数测试相同。

从图4可知：SOABCS与CSWA都能在较小代数内发现全局极值，但对全部全局极值点搜索时，SOABCS比CSWA有一定改善。CSWA能够分别发现2个(f₁函数)、6个(f₂函数)极值点后算法收敛，而SOABCS能够发现f₁，f₂，f₃函数的全部极值点，且搜索速度较快，说明算法运行过程中能较好保持种群多样性。

4.3  参数对算法的影响

通过迭代次数、函数极点搜索的测试，SOABCS算法能有效解决函数优化问题，但算法针对不同的函数因受到一些参数选择的影响，也会得到一些不同的结果。为此本文分别针对克隆规模、短连接邻域系数等参数对多极值函数的影响进行测试。

4.3.1  克隆规模对算法的影响

克隆算子将一个低维空间问题转化到更高维的空间中解决，然后再将结果投影到低维空间中，同时，从低维空间到高维空间转化过程中，存在着小世界长连接、短连接的变异操作，既能产生局部聚类的节点、又能够产生长连接节点，实现算法从局部到全局的搜索，从而更有效地解决问题，因此，克隆规模的选取是非常重要的。针对上述3个多极值函数，在保持其他参数不变的情况下，克隆规模在[1N，8N]范围内取值(N为种群规模)，按从小到大的方式独立试验50次，其归一化的平均迭代次数与迭代时间如图5所示。

图3  多极值函数SOABCS算法的解分布

Fig.3  Distributions of global optima in SOABCS

图4  SOABCS与CSWA极点搜索对比

Fig.4  Comparing of optima searched by SOABCS and CSWA

从图5可见，克隆规模越大，其迭代次数越小。在克隆规模较小(如1N~3N)时，3个多极值函数的算法迭代次数下降很快，但随着克隆规模的进一步扩大，算法迭代次数下降减慢。而对于算法迭代时间，f₁函数的算法迭代时间随着克隆规模增加而增加，8N时略有下降。f₂函数在2N时迭代时间最少，其余迭代时间随克隆规模成近似线性关系增加。f₃函数在3N~5N之间迭代时间变化不大，其他随克隆规模成近似线形  增长。

图5  克隆规模对算法的影响

Fig.5  Statistical results for clone scale

因此，当克隆规模为4N时，f₁，f₂，f₃函数的迭代次数与迭代时间都相对较佳。

4.3.2  短连接邻域系数对算法的影响

短连接邻域系数λ是确定两节点是否邻近的关键参数，由于在本算法中采用Hamming距离作为两节点的邻域度量，因此邻域系数对产生多样性也起到一定的促进作用。图6所示为短连接邻域系数λ在[1，5]内取整数值时f₁，f₂，f₃函数的归一化平均迭代次数与迭代时间。

从图6可知：当λ为1时，对f₁函数影响很大，在进行的50次试验中，多次无法达到算法收敛，其平均归一化迭代次数和迭代时间分别在0.6~0.7与0.5~0.6之间非真实比例关系，仅表示短连接邻域系数对其影响很大，在最大迭代次数限制内无法收敛到最优值。这是由于邻域系数过小，对于多极值f₁函数搜索空间变化缓慢，受种群初始化影响较大，当种群中较优抗体之间抗体-抗原亲和度差别不大时，其克隆机会接近，从而无法进行快速收敛。而f₂，f₃函数对于λ=1，2时，算法的迭代次数、时间变化不大，主要是因为极值点数目较少，即使较优个体间的适应度差别不大，但都在极值点附近，都向少数极值点移动，因此可以快速收敛。当λ≥3时，3个多极值函数的平均迭代次数、时间大致随邻域系数的增大而线性增加，这主要是由于短连接变化过大，加速抗体变异，破坏了抗体进化的相对稳定性，从而造成算法收敛效率下降。实验表明，当短连接系数λ为2时算法搜索效果较优。

图6  短连接系数对算法的影响

Fig.6  Statistical results for clustering coefficient

本文也对其他参数如全局长连接概率q_i等进行相关试验，结果与文献[6]结论类似，因此不再赘述。

5  结论

(1) 克隆算子与小世界变异算子相结合，利用小世界现象信息传递的高效性来改善种群变异进化的随机性，增加种群的多样性，扩大了搜索范围。

(2) 能将低维问题转化到较高维空间中解决，并将结果投影到低维空间中，保证在一代中多个优势抗体的同时进化，从而有利于多极值点函数寻优。

(3) 该算法是以克隆增殖、克隆选择及小世界短连接操作为特征的局部空间搜索方法，与以克隆删除与小世界长连接变异为基础的全局空间搜索策略有效结合，提高了算法的收敛速度和求解精度。

参考文献：

[1] Milgram S. The small world problem[J]. Psychology Today, 1967, 1(1): 61-67.

[2] Watts D, Strogatz S. Collective dynamics of small-worldnetworks [J]. Nature, 1998, 393: 440-442.

[3] Karsai M, Kivel? M, Pan R K, et al. Small but slow world: How network topology and burstiness slow down spreading[J]. Physical Review E, 2011, 83(2): 025102

[4] 杜海峰, 庄建, 张进华, 等. 用于函数优化的小世界优化算法[J]. 西安交通大学学报, 2005, 39(9): 1011-1015.
DU Hai-feng, ZHUANG Jian, ZHANG Jin-hua, et al. Small-world phenomenon for function optimization[J]. Journal of Xi'an Jiaotong University, 2005, 39(9): 1011-1015.

[5] 陈煜聪, 杨斌, 杜海峰, 等. 一种具有跟踪替代特征的小世界算法[J]. 西安交通大学学报, 2007, 41(11): 1360-1363.
CHEN Yu-cong, YANG Bin, DU Hai-feng, et al. Small-world algorithm with the replacing and tracking characters[J]. Journal of Xi'an Jiaotong University, 2007, 41(11): 1360-1363.

[6] 袁明新, 杜海峰, 王孙安, 等. 一种基于种群熵的混沌小世界优化算法[J]. 西安交通大学学报, 2008, 42(9): 1137-1141.
YUAN Ming-xin, DU Hai-feng, WANG Sun-an, et al. Chaos small-world optimal algorithm based on population entropy[J]. Journal of Xi'an Jiaotong University, 2008, 42(9): 1137-1141.

[7] 焦李成, 杜海峰, 刘芳, 等. 免疫优化计算、学习与识别[M]. 北京: 科学出版社, 2006: 24-25.
JIAO Li-cheng, DU Hai-feng, LIU Fang, et al. Immune optimization calculation, learning and recognition[M]. Beijing: Science Press, 2006: 24-25.

[8] Whitbrook A M, Aickelin U, Garibaldi J M. Real-world transfer of evolved artificial immune system behaviours between small and large scale robotic platforms[J]. Evolutionary Intelligence, 2010, 3(3) :123-136

[9] Newman M, Watts D. Scaling and percolation in the small-world network model[J]. Physical Review E, 1999, 60(6): 7332-7342.

[10] Laviolette R A, Ellebracht L A, Gieseler C J. Limits on relief through constrained exchange on random graph[J]. Physica A, 2007, 383: 671-676.

[11] 莫宏伟. 人工免疫系统原理与应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003: 24-27.
MO Hong-wei. The principle and application of artificial immune system[M]. Harbin: Harbin Institute of Technology Press, 2003: 24-27.

[12] 陈乃建, 王孙安, 邸宏宇, 等. 基于复杂网络特征的背包问题优化算法[J]. 系统工程与电子技术, 2009(9): 2232-2237.
CHEN Nai-jian, WANG Sun-an, DI Hong-yu, et al. Knapsack-problem optimization algorithm based on complex network[J]. Systems Engineering and Electronics, 2009(9): 2232-2237.

[13] Kleinberg J. The small-world phenomenon: An algorithmic perspective. [EB/OL]. [2004-11-20] http://www.cs.cornell.edu/ home/kleinber/swn.d/swn.html.

[14] 龚光鲁, 钱敏平. 应用随机过程教程及在算法和智能计算中的随机模型[M]. 北京: 清华大学出版社, 2004: 86-89.
GONG Guang-lu, QIAN Min-ping. Applying stochastic process tutorial and the stochastic model in algorithm and intelligent computation[M]. Beijing: Tsinghua University Press, 2004: 86-89.

[15] 施仁杰. 马尔科夫链基础及其应用[M]. 西安: 西安电子科技大学出版社, 1992: 6-8.
SHI Ren-jie. Markov chain and its application[M]. Xi’an: Xidian University Press, 1992: 6-8.

(编辑 赵俊)

收稿日期：2011-08-06；修回日期：2011-11-30

基金项目：山东省优秀中青年科学家科研奖励基金资助项目(BS2011DX003)；济南大学博士基金资助项目(XBS1101)

通信作者：陈乃建(1973-)，男，山东临沂人，博士，讲师，从事机器人及智能控制技术研究；电话：0531-82765476；E-mail：me_chennj@ujn.edu.cn