A two-stage CO-PSO minimum structure inversion using CUDA for extracting IP information from MT data
来源期刊:中南大学学报(英文版)2018年第5期
论文作者:李帝铨 董莉 江沸菠
文章页码:1195 - 1212
Key words:Cauchy oscillation particle swarm optimization; magnetotelluric sounding; nonlinear inversion; induced polarization (IP) information extraction; compute unified distributed architecture (CUDA)
Abstract: The study of induced polarization (IP) information extraction from magnetotelluric (MT) sounding data is of great and practical significance to the exploitation of deep mineral, oil and gas resources. The linear inversion method, which has been given priority in previous research on the IP information extraction method, has three main problems as follows: 1) dependency on the initial model, 2) easily falling into the local minimum, and 3) serious non-uniqueness of solutions. Taking the nonlinearity and nonconvexity of IP information extraction into consideration, a two-stage CO-PSO minimum structure inversion method using compute unified distributed architecture (CUDA) is proposed. On one hand, a novel Cauchy oscillation particle swarm optimization (CO-PSO) algorithm is applied to extract nonlinear IP information from MT sounding data, which is implemented as a parallel algorithm within CUDA computing architecture; on the other hand, the impact of the polarizability on the observation data is strengthened by introducing a second stage inversion process, and the regularization parameter is applied in the fitness function of PSO algorithm to solve the problem of multi-solution in inversion. The inversion simulation results of polarization layers in different strata of various geoelectric models show that the smooth models of resistivity and IP parameters can be obtained by the proposed algorithm, the results of which are relatively stable and accurate. The experiment results added with noise indicate that this method is robust to Gaussian white noise. Compared with the traditional PSO and GA algorithm, the proposed algorithm has more efficiency and better inversion results.
Cite this article as: DONG Li, LI Di-quan, JIANG Fei-bo. A two-stage CO-PSO minimum structure inversion using CUDA for extracting IP information from MT data [J]. Journal of Central South University, 2018, 25(5): 1195–1212. DOI: https://doi.org/10.1007/s11771-018-3818-4.

J. Cent. South Univ. (2018) 25: 1195-1212
DOI: https://doi.org/10.1007/s11771-018-3818-4
DONG Li(董莉)1, 2, 4, LI Di-quan(李帝铨)1, JIANG Fei-bo(江沸菠)1, 3
1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
2. School of Information Science and Engineering, Hunan International Economics University,Changsha 410205, China;
3. College of Information Science and Engineering, Hunan Normal University, Changsha 410081, China;
4. School of Computer and Information Engineering, Hunan University of Commerce, Changsha 410205, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: The study of induced polarization (IP) information extraction from magnetotelluric (MT) sounding data is of great and practical significance to the exploitation of deep mineral, oil and gas resources. The linear inversion method, which has been given priority in previous research on the IP information extraction method, has three main problems as follows: 1) dependency on the initial model, 2) easily falling into the local minimum, and 3) serious non-uniqueness of solutions. Taking the nonlinearity and nonconvexity of IP information extraction into consideration, a two-stage CO-PSO minimum structure inversion method using compute unified distributed architecture (CUDA) is proposed. On one hand, a novel Cauchy oscillation particle swarm optimization (CO-PSO) algorithm is applied to extract nonlinear IP information from MT sounding data, which is implemented as a parallel algorithm within CUDA computing architecture; on the other hand, the impact of the polarizability on the observation data is strengthened by introducing a second stage inversion process, and the regularization parameter is applied in the fitness function of PSO algorithm to solve the problem of multi-solution in inversion. The inversion simulation results of polarization layers in different strata of various geoelectric models show that the smooth models of resistivity and IP parameters can be obtained by the proposed algorithm, the results of which are relatively stable and accurate. The experiment results added with noise indicate that this method is robust to Gaussian white noise. Compared with the traditional PSO and GA algorithm, the proposed algorithm has more efficiency and better inversion results.
Key words: Cauchy oscillation particle swarm optimization; magnetotelluric sounding; nonlinear inversion; induced polarization (IP) information extraction; compute unified distributed architecture (CUDA)
Cite this article as: DONG Li, LI Di-quan, JIANG Fei-bo. A two-stage CO-PSO minimum structure inversion using CUDA for extracting IP information from MT data [J]. Journal of Central South University, 2018, 25(5): 1195–1212. DOI: https://doi.org/10.1007/s11771-018-3818-4.
1 Introduction
Induced polarization (IP) is a physicochemical phenomenon that arises from charge separation within the medium because of external current induction, which leads to an additional “over voltage” [1]. An effective geophysical technique, the induced polarization method, which is based on the IP property of rocks and ores, has been widely applied in the search for minerals, groundwater, oil, gas, and seismologic surveillance.
The IP effect is easily affected by varying external electromagnetic (EM) field including man-made source and natural source. And it would be inaccurate and inadequate if IP effect is ignored in theoretical research and survey work of EM field. As early as the 1970 s, the feasibility of IP measurement for the natural EM field was discussed [2, 3]. MURALI et al [4] measured the telluric field, together with time domain IP over a mineralised zone in Madhya Pradesh, India. The results of the telluric field data agreed qualitatively with time domain IP data. GASPERIKOVA et al [5] introduced natural field induced polarization to map deep mineral deposits. GHORBANI et al [6] constructed an open source inversion MATLAB code to recover 1D parameters of spectral induced polarization data for the Cole-Cole model including electromagnetic effects. YUE et al [7] introduced the basic theory and method of extracting the induced polarization information from a CSAMT signal, and they also studied the forward modeling of IP response with CSAMT 1D layered model on the basis of Dias model, which provided the theory foundation for the IP extraction from CSAMT signal. HE et al [8] used a type of magnetotelluric (MT) profiling called 3D continuous electromagnetic profiling (CEMP) to predict and delineate gas reservoirs. In their case study, a known gas-bearing formation had a high-resistivity anomaly and a high IP anomaly. YU et al [9] adopted Cole-Cole model to analyse the IP effect on the transient electromagnetic method (TEM) response in a homogeneous half space model and used singular value decomposition (SVD) to invert the measured TEM data in the mine area. TANG et al [10] chose an IP model that is best suited for the manipulation in MT forward and inversion by calculating and analyzing the sensitivity and integrated sensitivity of apparent resistivity to the different IP model parameters.
The traditional linear inversion methods are the major approaches used for polarizability extraction. Although they are simple and well- qualified for engineering needs, linear local search techniques (i.e., the conjugate gradient method, the least squares method, and the generalized inverse method) require a very good initial solution that is close to the true model for successful convergence. Generally considered a high-efficiency global optimization technique, particle swarm optimization (PSO) is a versatile particle optimizer that is valued for its simplicity, fast convergence and less parameter. It has been successfully applied to solving a wide range of global optimization problems. SHAW et al [11] inverted three noise-corrupted synthetic sounding data sets over a multilayered 1D earth model by using the PSO method. YUAN et al [12] used the PSO algorithm in three different types of geophysical inversion problems. Compared with the quasi-Newton method and Levenberg- Marquardt method, the algorithm worked better because of its ability to overcome locally optimal solutions. JIANG et al [13] presented a two-stage learning ICPSO algorithm of radial basis function neural network (RBFNN) based on information criterion and particle swarm optimization to improve the global search ability and imaging quality of electrical resistivity imaging (ERI) inversion. Although PSO inversion makes the interpretation more generalizable and more accurate than the linear approaches, the following inadequacies for interpreting the MT data with IP effect by the standard PSO algorithm still exist:1) When we take the IP effect into consideration, the resistivity of the polarizable body becomes a complex number that is related to frequency. The PSO algorithm has lower calculation efficiency in which the ground wave impedance of each frequency point needs to be calculated, leading to an increase in the computation burden of the forward iteration; 2) In addition to resistivity and thickness, the IP parameter is added to the inversion model parameter for MT inversion with IP effect. The increase of the inversion parameter makes the false structure inverted more easily by PSO method;3) The intensity of the electromagnetic anomaly is far greater than that of the IP anomaly. The nonlinear inversion algorithm generally converges to the adjacent domain of the true resistivity efficiently but enters into the local extremum easily when inverting the polarizability. Therefore, more researches about IP information extraction are necessary to achieve its stable convergence, to reduce the computing time and to obtain a global optimal solution.
In this work, a two-stage CO-PSO minimum structure inversion method for IP information extraction is proposed and compute unified distributed architecture (CUDA) is adopted in the proposed algorithm for better implementation efficiency. The inversion process is based on the MT signal forward research encompassing the IP effect and the Dias complex resistivity model. A novel Cauchy oscillation particle swarm optimization (CO-PSO) algorithm is applied to improve the global searching ability of PSO by setting inertia weight w adapted from the Cauchy distribution and oscillatory descending. The impact of the polarizability is strengthened by introducing a second stage inversion process. To overcome the overcomplicated problem of inverting the model, the minimum structure restrictions is imposed in the fitness function of PSO algorithm to eliminate the redundant structure in the proposed scheme, which results in a stable and robust inversion outcome. Finally, the proposed inversion method is implemented in CUDA computing architecture. The results show that the proposed inversion algorithm performs better than traditional PSO and GA methods in efficiency, stability and accuracy, which produces a satisfactory outcome of the IP information and an explicit boundary of the geoelectric structures.
2 Theoretical background
2.1 Dias model
The Dias model [14, 15] is applied to simulating the IP effect of the geological media. The equivalent fundamental circuit analog as the unit cell for electrical polarization of rocks is shown in Figure 1.
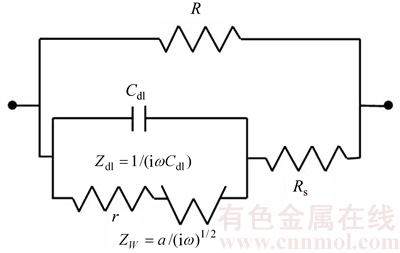
Figure 1 Equivalent circuit of Dias mode
The expression for complex resistivity, which is associated with the circuit analog of Figure 1, is given by:
 (1)
(1)
where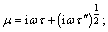
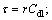
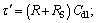
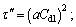 η=a/r;
η=a/r;

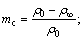 ρ0 is the real DC value of ρ(ω);
ρ0 is the real DC value of ρ(ω);
Relaxation time τ is positive and is related to the average size of the particles producing polarization; the electrochemical parameter η is related to the characteristics of the electrochemical environment producing polarization, which is related to the relative significance between the ohmic (induced) electrical current component and the modulus of the diffusion-produced component inside the electrical double layer at 1 rad/s frequency in the unit cell; pore length fraction δ is dimensionless and is defined on the interval 0≤δ<1. It refers solely to the pore path that represents the locus where polarization is produced; chargeability mc is dimensionless and is defined in the interval 0≤mc<1. To date, it has been the best defined and most reliable parameter used to identify rock polarization in field measurements. Its value is commonly associated with the intensity of the polarization effect.
2.2 Forward modelling
The MT impedance Z0(ω) at the surface of an n-layered earth for an incident plane wave with angular frequency ω can be written as [11]:
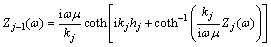 (2)
(2)
where  represents the wave number of the jth layer of conductivity σj and thickness hj; μ
represents the wave number of the jth layer of conductivity σj and thickness hj; μ represents the permeability of free space and
represents the permeability of free space and 
The apparent resistivity ρa(ω) and apparent phase φa(ω) are related to the MT impedances as
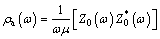 (3)
(3)
 (4)
(4)
where  represents the complex conjugate of Z0(ω).
represents the complex conjugate of Z0(ω).
When we take the IP effect into consideration, the real resistivity is replaced by the complex resistivity given by Eq. (1) to obtain the comprehensive response of the IP effect and electromagnetic effect.
2.3 Particle swarm optimization
Particle swarm optimization (PSO) is an evolutionary computation technique that was originally developed by KENNEDY et al [16]. It is inspired by the social behavior of flocks of birds when they are searching for food. In the PSO searching space, the potential solutions are called particles. This algorithm simulates the collaboration among a population of particles to find optimum in the problem space. The position of a particle is influenced by the best position visited by itself and the position of the best particle in its neighbourhood. Every particle has a fitness value, which is evaluated by the fitness function to be optimized and a velocity that directs the trajectory of the particle. The details of PSO are described as follows.
The position vector and velocity vector of the ith particle in p-dimensional space are represented as xi=(xi1, xi2, …, xip) and vi=(vi1, vi2, …, vip), respectively. In the search process, each particle knows its best previous position pbi and current position xi. In addition, each particle also knows the best previous position pg among all particles in the swarm (pg is the optimal value among all pbi). Each particle constantly updates using its own experience and its neighbours’ experiences to produce the next generation swarm. The velocity update formula and position update formula are described as follows [15]:

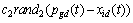 (5)
(5)
 (6)
(6)
where c1 and c2 are acceleration coefficients which are nonnegative constants; rand1 and rand2 are generated randomly in the interval [0,1]; t is the current iteration; pbid(t) is the best position of the ith particle; pgd(t) is the best particle position among all the particles; d=1, 2, …, p.
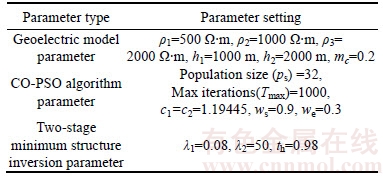
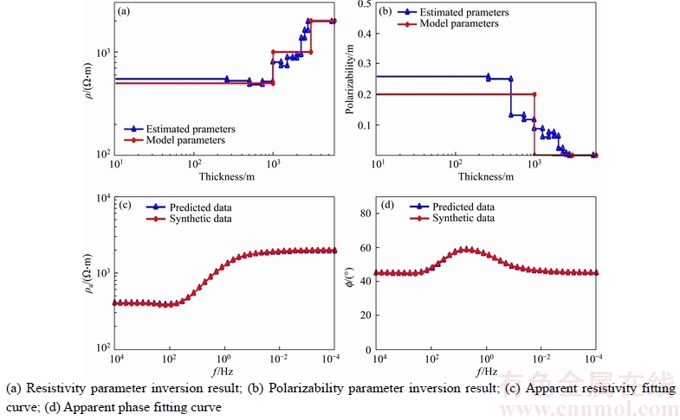
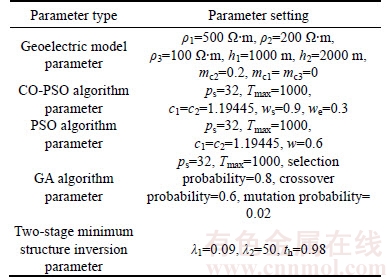
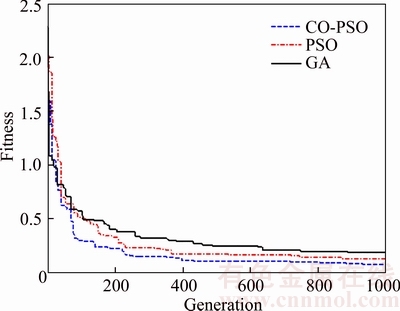
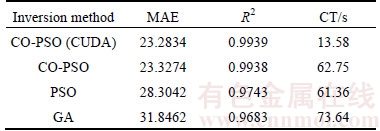
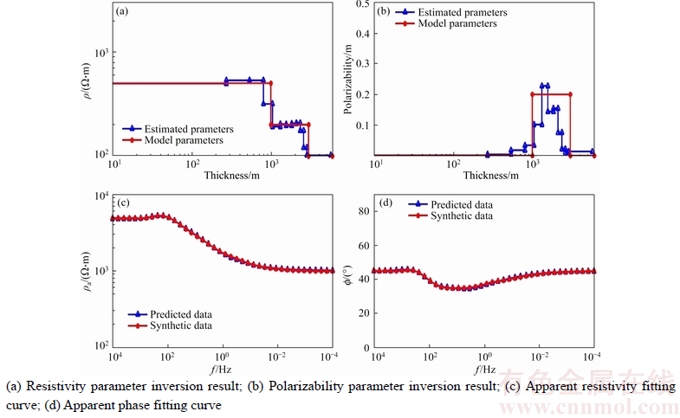
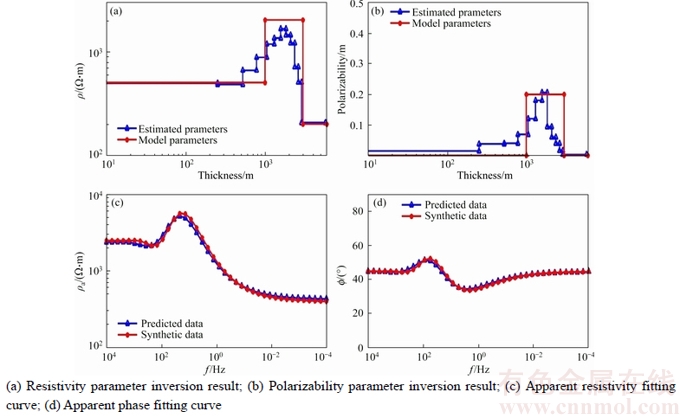
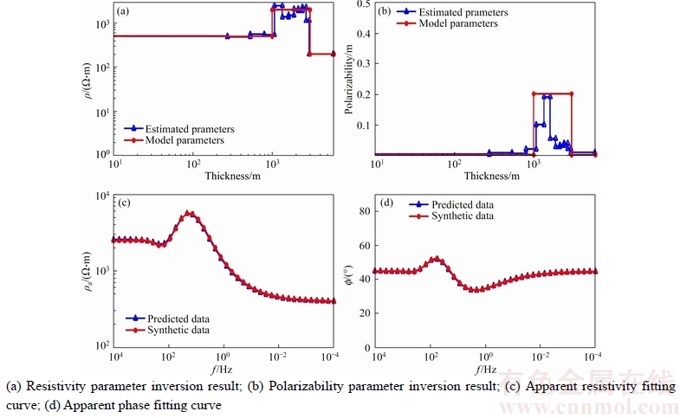
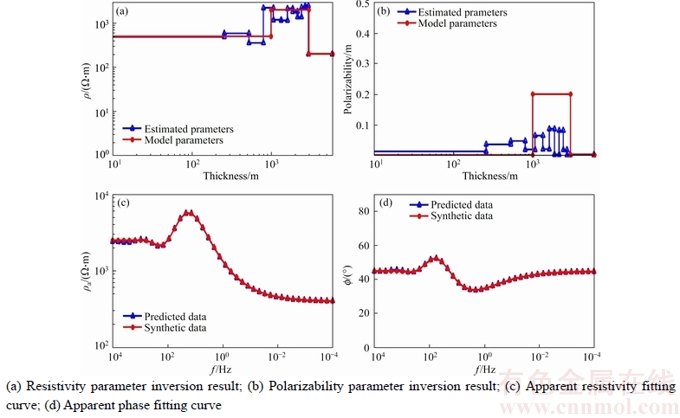
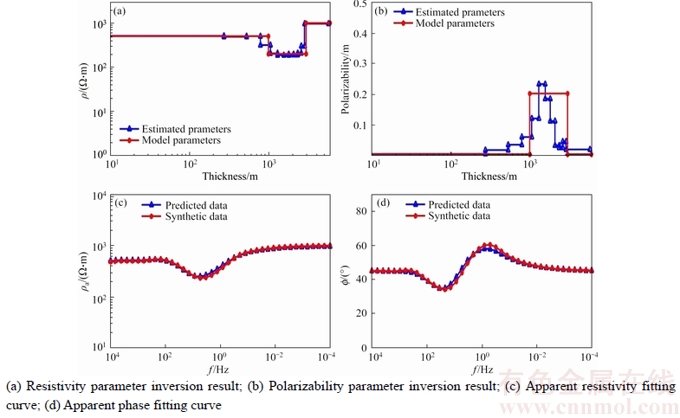
In Eq.(5), the inertia weight w(t) affects the contribution of vid(t) to the new velocity vid(t+1). Thus, if w(t) is large, it makes a large step in one iteration (exploring the search space), whereas if w(t) is small, it makes a small step in one iteration and therefore tends to stay in a local region (exploiting the search space). Typically, the inertia weight is set to 0.4 2.4 Cauchy oscillation particle swarm optimization (CO-PSO) The intensity of the electromagnetic anomaly is far greater than that of the IP anomaly; therefore, it is very difficult to extract the tiny IP information drowned out by the strong EM effect. To extract IP information from MT data, the global searching ability of the inversion approach needs to be improved to fit the observation date accurately, even if the value changes inconspicuously; meanwhile, it is necessary to highlight the influence of the IP anomaly to the fitness function. Classical PSO benefits from its fast convergence by guiding the evolutionary search with the best solution so far discovered, thereby converging faster to that solution. However, as a result of such exploitative tendencies, in the IP information extraction case, the population may lose its diversity and global exploration abilities within relatively few generations, thereafter getting trapped to some locally optimal solution in the search space. Therefore, there is still a need for improving the search performance of PSO to face the challenges from the IP information extraction areas. Earlier theoretical studies have indicated that the inertia weight w(t) has a big role in controlling the global searching ability of PSO. Taking these facts into consideration and in an effort to overcome the limitations of the less reliable classical PSO scheme, we propose a Cauchy oscillation particle swarm optimization scheme. In the new scheme, the inertia weight w(t) is replaced by a Cauchy oscillation inertia weight wco(t), which can be expressed as: where ws is the initial weight; we is the final weight; wc(t) is a random number sampled from a Cauchy distribution in the following way: where wm(t) is the location parameter and 0.1 is the scale parameter of Cauchy distribution. The value of wc(t) is regenerated if wc(t)≤0 or wc(t)>1. wm(t) is calculated as: Denote wsuccess as the set of successful inertia weight, so far, of the current generation generating better particles and fitness values that are likely to advance to the next generation; meanp stands for the power mean given by: With n denoting the cardinality of the set wsuccess, p is set to 1.5 by trial and error. In CO-PSO scheme, the oscillatory descending w is applied to controlling the relation between local exploitation and global exploration in the search process. The Cauchy distribution has a far wider tail than traditional uniform distribution, and it is beneficial when the global optima is far away from the current search point as the values of wco(t) taken from the tail region give sufficient perturbation so that premature convergence can be avoided. The usage of power mean leads to higher value of wco(t) that accounts for large perturbation to the population, thus avoiding premature convergence at local optima. The essence of wsuccess is that it memorizes the successful wco(t) in the current generation, thereby increasing the chance of creating better particles in evolutionary process. 2.5 CUDA implementation Recently, the graphics processing unit (GPU) has emerged as a powerful computation device and modern graphics hardware has gained an important role in the area of parallel computing. Compute unified distributed architecture (CUDA) is a general purpose GPU environment by NVIDIATM available for most recent GPUs. The CUDA library can be used by FORTRAN, C, C++, and by other languages and it is easily programmed. In CUDA architecture, a parallel program on a GPU (also termed device) is interleaved with a serial one executed on the CPU (also termed host). A thread block has a stream of threads executed concurrently on a multiprocessor, which has synchronized access to a shared memory. However, threads originating from different blocks cannot be cooperated in this way. These thread blocks are combined to form a grid. All the threads in the grid can access the same global memory. Threads are enumerated and distributed to multiprocessor when a CUDA code on the CPU calls a kernel function. In recent years, implementations of algorithms in CUDA computing architecture to solve scientific problems have appeared with promising results [18–21]. Swarm intelligence techniques are intrinsically parallel because every swarm member has few dependencies on the others, so all operations aimed at adapting an individual’s values, like position update or fitness evaluation, can be executed with few (or none at all) interactions with the other elements of the swarm. In order to obtain high- efficiency inversion results, some specific programming guidelines should be followed, the most important of which are: 1) Minimize the use of global memory and shared memory should be preferred; 2) Minimize data transfers between the host and the device. According to the programming guidelines, we have optimized the parallelized architecture. In the parallelized PSO algorithm, the population is divided into many threads as the number of particles, each thread implements the update formula for one particle. The most salient feature of this way is the absence of accesses to the global memory. As regards thread memory allocation, each particle stores its current positon, velocity, best positon and best fitness values in local thread registers and all these parameters are kept in the shared memory of the corresponding thread block, in order to permit communication between particles. The parallelized architecture of our PSO algorithm based CUDA is shown in Figure 2. Our CUDA-based implementation of CO-PSO has three CUDA kernel functions: Update, Evaluation and Findpg. Kernel function Update is used to modify the position, individual optimal position and velocity of each particle in the population for each thread. Kernel function Evaluation is used to calculate the fitness of each particle. Kernel function Findpg is applied to finding the optimal fitness and the optimal index. Figure 2 Parallelized architecture of PSO algorithm based CUDA In summary, we implements the CO-PSO algorithm using three CUDA kernel functions, within which each particle in the swarm is simulated by a single thread. Only one thread block is needed to simulate the whole population. 3 Inversion schemes 3.1 Two-stage minimum structure inversion The IP information extraction inverse problem can be formulated as an optimization problem aimed at finding the model that best explains a set of observed data. Consider the mapping F between the model space m and the data space d as [11]: The data space d is given by N apparent resistivity values as ρa=[ρa1, ρa2, …, ρaN], and the model space m is given by the model parameters of l layers as m=[mc1, mc2, …, mcl, ρ1, ρ2, …, ρl, h1, h2, …, hl–1] consisting of (3l–1) model parameters. mci, ρi and hi are the polarizability, resistivity and thickness of layer i, respectively. Under the assumption that the true earth mtrue lies inside the model space, and the observed datum aobs is noise free, the equation can be written as: Therefore, the inversion requires three elements as follows: 1) a forward model F that computes the transfer impedances, 2) an objective function that states the model fitting criteria and 3) a search algorithm which determines the way in which the “optimum” model mtrue is found. In this paper, the forward model F is given in Section 2.2; PSO is employed as the search algorithm, and the objective function is defined as follows: where R(ρ) and R(mc) are regularization terms that contain the a priori knowledge about the solution ρ and mc; λ1 and λ2 are the regularization parameters that balance the effect of data misfit and model regularization during minimization [22]; R(ρ) and R(mc) can be calculated as follows [23]: where mi is thought to be mci or ρi obtained from the inversion process. E(e) is the data misfit term, which can be calculated as follows [24]: where where ρ=[ρ1, ρ2, …, ρl] and mc=[mc1, mc2, …, mcl] are the resistivity and polarization parameters obtained from the inversion process, respectively; h=[h1, h2, …, hl–1] is the thickness of the layer; th is the threshold value; R2 is the correlation coefficient. The proposed IP information extraction process is a two-stage inversion process based on CO-PSO algorithm. In the first stage, ρ, mc and h are applied in CO-PSO inversion process. The individuals of CO-PSO will quickly converge around the correct value ρ, and R2 will increase rapidly. If R2 reaches the threshold value th, the ρ search is complete, and the inversion will move into the second stage. In the second stage, only mc is employed to the CO-PSO inversion process; ρ and h are fixed. Finally, the individuals of CO-PSO will converge around the correct value mc when a sufficient number of iterations is reached. 3.2 Complete algorithm description The proposed two-stage CO-PSO minimum structure inversion algorithm is a framework for efficient implementation of extracting IP information from MT data. A short review of the proposed approach is summarized below: Step 1: Perform CO-PSO algorithm for parameters optimization in stage one. Step 1.1: Initialize population. Create a swarm of particles as the initial population of CO-PSO and generate each parameter xi, vi randomly according to the model parameters ρ, mc and h. Step 1.2: Calculate fitness. Calculate the fitness of each target particle by Eqs. (13)–(16). Step 1.3: Evaluate the population. Evaluate the fitness value for each particle using the fitness function. Replace the best position pbid and the global best position pgd if they improved in this generation. If R2 satisfies a predefined criterion th, save the result and go to Step 2; otherwise, go to Step 1.4. Step 1.4: Particle optimization. Update the velocity and position using Eqs. (5)–(10) to generate a new population for next generation, and then go to Step 1.2. Step 2: Perform CO-PSO algorithm for polarizability parameters optimization in stage two: Step 2.1: Fix ρ and h, update the velocity and position using Eqs. (5)–(10) to generate a new population for next generation, and then go to Step 2.2. Step 2.2: Calculate fitness. Calculate the fitness of each target particle by Eqs.(13)–(16). Step 2.3: Evaluate the population. Evaluate the fitness value of each particle using fitness function. Replace the best position pbid and the globe best position pgd if they are better in this generation. If R2 satisfies a predefined criterion th or the max generation is reached, save the result and go to Step 3; otherwise, go to Step 2.1. Step 3: Use the global best position of the CO-PSO algorithm as ρ, mc and h and complete the two-stage PSO minimum structure inversion process. The outline of the procedure to IP information extraction using the proposed method with CUDA implementation is presented in Figure 3. 4 Examples and results 4.1 Evaluation indicators To evaluate the performance of the proposed inversion method for IP information extraction from MT data, two precision indexes between measured values and predicted values are defined as follows [25]: In the above parameters, R2 is calculated to analyze the accuracy of predicted values versus measured values. It ranges from 0 to 1. The higher the R2 value, the stronger the indication of an existing linear relationship between the measured and predicted values, whereas the MAE indicates less prediction error. The computer simulation is estimation error. With lower MAE value, there is taken in the operating environment of Windows 7 (64 bit) with Intel i5-3230M CPU, 4GB DDR3 RAM and GT 630M GPU. The GT 630M GPU has 96 CUDA cores, 1GB RAM and 800 MHz processor clock. Figure 3 Flowchart of proposed inversion method using CUDA Table 1 Equations of evaluation parameters for inversion model 4.2 A-type three-layered geoelectric model inversion We use an A-type three-layered geoelectric model to verify the inversion results of polarized layer in different strata. The considered values to set parameters of the inversion process are shown in Table 2. Table 2 Parameter setting for A-type three-layered model inversion The evaluation indicators of inversion results are shown in Table 3. The results of evaluation indicators show that the proposed method in Stage 2 achieves better R2 and MAE than in Stage 1. This is because the CO-PSO algorithm in Stage 2 is used to fine-tune the polarization parameter mc and find the better mc according to the ρ and h selected in Stage 1. With the new mc, the two-stage inversion method has better performance. Table 3 also shows that the A-type three-layer model with polarized middle layer consistently has the higher R2 value and the lower MAE value compared with the other two cases. Figures 4–6 offer further inversion results and fitting curves. In all these cases, inversion results depict resistivity and polarizability parameters. The proposed two-stage inversion method reconstructs the A-type three-layered model successfully, in accordance with the theoretical calculation. Table 3 Inversion results of IP information extraction for A-type three-layered model Figure 4 Inversion results of A-type three-layered model with polarized first layer (mc1=0.2, mc2=mc3=0) Figure 5 Inversion results of A-type three-layered model with polarized middle layer (mc2=0.2, mc1=mc3=0) Figure 6 Inversion results of A-type three-layered model with polarized lower layer (mc3=0, mc1=mc2=0) 4.3 Q-type three-layered geoelectric model inversion We use a Q-type three-layered geoelectric model with a polarized middle layer to verify the inversion results employing different global searching algorithms (such as CO-PSO, PSO and GA). Parallelization is also a very important strategy for reducing the computing time to the proposed algorithm. So, we evaluate the execution time of our CO-PSO inversion algorithm using CUDA implementation. Note that the time associated with the data transfer between CPU and GPU is included in execution time for the CO-PSO with GPU acceleration. The values considered to set parameters of the inversion process are shown in Table 4. Remarkably, we set Ps=32, which is a reasonable number of threads. In most GPUs, there are 32 stream processors in a multiprocessor, so we take the number as multiple of the number of steam processors. Table 4 Parameter settings for different global searching algorithms inversion Figure 7 shows the convergence curves of different global searching algorithms in the inversion process. The convergence curve obtained by the CO-PSO method declines sharply at the beginning of procedure and then decreases slowly in later stages; the same phenomenon occurs using the traditional PSO and GA methods, as seen in Figure 7. The CO-PSO method has a greater convergence rate and lower fitness value than the PSO and GA methods. The CO-PSO method performs better than or at least comparable with the PSO and GA methods in the inversion process. The inversion results of the MAE, the R2 and the corresponding computing time (CT) are listed in Table 5. Figure 7 Fitness convergence curves of different global searching algorithms Table 5 Inversion results of IP information extraction for three-layered model using different global searching algorithms It is not difficult to see from these results that, on the whole, the accuracy of CO-PSO and CO-PSO (CUDA) presents an obvious advantage compared to that of PSO and GA. The main reason is that, CO-PSO utilizes the Cauchy random operator for inertia weight w generation, which increases the particle’s search range randomly and enhances the optimization capability of the algorithm, and besides, oscillatory descending w is applied to controlling the relation between local exploitation and global exploration in the search process. The two measures enhance the global search capability and convergence performance in optimization of the IP information search, and avoid the premature convergence to a great extent. Therefore, the CO-PSO inversion method is feasible and effective for extracting IP information. It also shows that, for parallelization optimization of CO-PSO that we care for, CUDA has great advantage by contrast with traditional CPU implementation. The speedup of CO-PSO (CUDA) is 4.62 over CO-PSO, which is defined as sequential computing time over parallel computing time. Thus, CUDA is an efficient and effective approach towards the inversion acceleration, especially for large scale inversion problem. Figure 8 offers a further indication of the inversion results and the fitting curves of the CO-PSO inversion method with the two-stage minimum structure procedure. We can see the proposed inversion method reconstructs the Q-type three-layered geoelectric model with the polarized middle layer, agreeing well with the theoretical calculation. 4.4 K-type three-layered geoelectric model inversion We employ a K-type three-layered geoelectric model with a polarized middle layer to verify the inversion results using different regularization parameters λ1 and λ2. The considered values to set the parameters of the inversion process are shown in Table 6. The performance using different regularization parameters λ1 and λ2 is compared in Table 7, and Figures 9–11 offer further inversion results and fitting curves. The regularization parameters λ1 and λ2 can influence the complexity and smoothness of the inversion results, and an important task of the proposed inversion method is to select the appropriate values of parameters λ1 and λ2 for the minimum construction inversion. 4.5 H-type three-layered geoelectric model inversion In field data collection, we inevitably observe some kind of noise which creeps into the field observations and corrupts the signal [26–28]. We use an H-type three-layered geoelectric model with a polarized middle layer to verify the inversion results with different IP models: Dias model and Cole-Cole model. The Dias model fits to descript IP effect at high frequencies in MT, and the Cole-Cole model acts better at lower frequencies [10]. The considered values to set the parameters of the inversion process are shown in Table 8. The evaluation indicators are shown in Table 9. The detailed inversion performance of these IP models can be seen in Figures 12 and 13. We can see that the proposed method is feasible for extraction of IP information using different IP models in MT data, and it reconstructs the H-type three-layered geoelectric model with different IP models successfully. Compared with Cole-Cole model, Dias model has better inversion performance and higher inversion accuracy in this case. Figure 8 Inversion results of Q-type three-layered model with polarized middle layer Table 6 Parameter settings for K-type three-layered model inversion Table 7 Inversion results of IP information extraction for three-layered model using different regularization parameters Figure 9 Inversion results of K-type three-layered model with polarized middle layer (λ1=0.1,λ2=50) 4.6 HKH-type five-layered geoelectric model inversion We use an HKH-type five-layered geoelectric model with a polarized middle layer to verify the inversion results with different levels of noise. The considered values to set the parameters of the inversion process are shown in Table 10. The evaluation indicators are shown in Table 11, and the match between the observed and the synthetic data is shown in Figures 14–16. The model MAE values for 0, 10% and 20% noisy data inversions are 0.1917, 0.8854 and 1.4253, respectively. The correlation coefficient R2 values for 0%, 10% and 20% noisy data inversions are 0.9991, 0.9075 and 0.8633, respectively. Although the noise increased, the inversion results are stable, which reflects the robustness of the proposed inversion algorithm. Figure 10 Inversion results of K-type three-layered model with polarized middle layer (λ1=0.001,λ2=50) Figure 11 Inversion results of K-type three-layered model with polarized middle layer (λ1=0.001,λ2=0.5) Table 8 Parameter setting for H-type three-layered model inversion Table 9 Inversion results of IP information extraction for H-type three-layered model using different IP models Figure 12 Inversion results of H-type three-layered model with polarized middle layer using Dias model 5 Conclusions This paper introduces a novel two-stage CO-PSO minimum structure inversion algorithm for extracting IP information from MT sounding data. The inversion results show that the proposed method demonstrates feasibility and effectiveness for layered model inversion. The main contributions of this research include: Figure 13 Inversion results of H-type three-layered model with polarized middle layer using Cole-Cole model Table 10 Parameter setting for HKH-type five-layered model inversion Table 11 Inversion results of IP information extraction for HKH-type five-layered noisy model 1) The proposed method adopts the forward modelling method of MT sounding data with the Dias model. 2) The resistivity, polarizability and thickness of the layered model are searched by a novel CO-PSO algorithm. In the proposed method, the values of inertia weight are taken from the Cauchy distribution and oscillatory descending for avoiding premature convergence. 3) The impact of the polarizability on the observation data is strengthened by introducing a second stage inversion process. 4) The regularization parameter is applied in the fitness function of CO-PSO algorithm to solve the problem of multi-solution in inversion. 5) The CO-PSO inversion algorithm is implemented with three CUDA kernel functions on the CUDA architecture. Each particle in the swarm is simulated by a single thread. This strategy can minimize the use of global memory. Figure 14 Inversion results of HKH-type five-layered noiseless model with polarized middle layer Figure 15 Inversion results of HKH-type five-layered noisy model with polarized middle layer (10% noise) Figure 16 Inversion results of HKH-type five-layered noisy model with polarized middle layer (20% noise) In a word, the proposed method is a direct approach to a non-linear task, which avoids linearization and the choice of appropriate starting models as necessary for classical minimization methods. It can be applied to more complex synthetic data and field data, which will be explored in further research. References [1] HE Ji-shan. Dual frequency induced polarization method [M]. Beijing: Higher Education Press, 2006. (in Chinese) [2] WU Han-rong, WANG Shi-ming. The feasibility of nature source induced polarization [J]. Geophysical and Geochemical Exploration, 1978(1): 62–64. (in Chinese) [3] WARE G. Theoretical and field investigations of telluric currents and induced polarization [D]. Berkeley: University of California at Berkeley, 1974. [4] MURALI S, RAO I B R, BHIMASANKARAM V L S, Comparison of anomalous effects determined using telluric fields and time domain IP technique (test results) [J]. Exploration Geophysics, 1980, 11(2): 45–46. DOI: 10.1071/EG980045. [5] GASPERIKOVA E, MORRISON H F. Mapping of induced polarization using natural fields [J]. Geophysics, 2001, 66(1): 137–147. DOI: 10.1190/1.1444888. [6] GHORBANI A, CAMERLYNCK C, FLORSCH N. CR1Dinv: A matlab program to invert 1D spectral induced polarization data for the Cole–Cole model including electromagnetic effects [J]. Computers & Geosciences, 2009, 35(2): 255–266. DOI: 10.1016/j.cageo.2008.06.001. [7] YUE An-ping, DI Qing-yun, WANG Miao-yue. 1-D forward modeling of the CSAMT signal incorporating IP effect [J]. Chinese Journal of Geophysics, 2009, 52(7): 1937–1946. (in Chinese). DOI: 10.1002/cjg2.1411. [8] HE Zhan-xiang, HU Zu-zhi, LUO Wei-feng, WANG Cai-fu. Mapping reservoirs based on resistivity and induced polarization derived from continuous 3D magnetotelluric profiling: Case study from Qaidam basin, China [J]. Geophysics, 2010, 75(1): B25–B33. DOI: 10.1190/1. 3279125. [9] YU Chuan-tao, LIU Hong-fu, ZHANG Xin-jun. The analysis on IP signals in TEM response based on SVD [J]. Applied Geophysics, 2013, 10(1): 79–87. DOI: 10.1007/S11770-013- 0366-4. [10] TANG Rui, XU Peng, XIANG Yang, ZHANG Xu. The sensitivity analysis of different induced polarization models used in magnetotelluric method [J]. Acta Geodaetica et Geophysica, 2014, 49(2): 225–233. DOI: 10.1007/s40328-014-0050-z. [11] SHAW R, SRIVASTAVA S. Particle swarm optimization: A new tool to invert geophysical data [J]. Geophysics, 2007, 72(2): F75–F83. DOI: 10.1190/1.2432481. [12] YUAN San-yi, WANG Shang-xu, TIAN Nan. Swarm intelligence optimization and its application in geophysical data inversion [J]. Applied Geophysics, 2009, 6(2): 166–174. DOI: 10.1007/s11770-009-0018-x. [13] JIANG Fei-bo, DAI Qian-wei, DONG Li. An ICPSO-RBFNN nonlinear inversion for electrical resistivity imaging [J]. Journal of Central South University, 2016, 23(8): 2129–2138. DOI: 10.1007/s11771-016-3269-8. [14] DIAS C A. A non-grounded method for measuring electrical induced polarization and conductivity [D]. Berkeley: University of California, 1968. [15] DIAS C A. Developments in a model to describe low- frequency electrical polarization of rocks [J]. Geophysics, 2000, 65(2): 437–451. DOI: 10.1190/1.1444738. [16] KENNEDY J, EBERHART R. Particle swarm optimization [C]// IEEE International Conference on Neural Networks. Proceedings. IEEE Xplore, 1995: 1942–1948. [17] NABAVI-KERIZI S H, ABADI M, KABIR E. A PSO-based weighting method for linear combination of neural networks [J]. Computers & Electrical Engineering, 2010, 36(5): 886–894. DOI: 10.1016/j.compeleceng.2008.04.006. [18] MUSSI L, DAOLIO F, CAGNONI S. Evaluation of parallel particle swarm optimization algorithms within the CUDATM architecture [J]. Information Sciences, 2011, 181(20): 4642–4657. DOI: 10.1016/j.ins.2010.08.045. [19] OUYANG Ai-jia, TANG Zhou, ZHOU Xu, XU Yu-ming, PAN Guo, LI Ke-qin. Parallel hybrid PSO with CUDA for lD heat conduction equation [J]. Computers & Fluids, 2015, 110(30): 198–210. DOI: 10.1016/j.compluid.2014.05.020. [20] DALI N, BOUAMAMA S. GPU-PSO: Parallel particle swarm optimization approaches on graphical processing unit for constraint reasoning: case of Max-CSPs [J]. Procedia Computer Science, 2015, 60(1): 1070–1080. DOI: 10.1016/ j.procs.2015.08.152. [21] UGOLOTTI R, NASHED Y S G, MESEJO P, LVEKOUI, MUSSI L, CAGONI S. Particle swarm optimization and differential evolution for model-based object detection [J]. Applied Soft Computing, 2013, 13(6): 3092–3105. DOI: 10.1016/j.asoc.2012.11.027 [22] JIANG Fei-bo, DAI Qian-wei, DONG Li. Ultra-high density resistivity nonlinear inversion based on principal component-regularized ELM [J]. Chinese Journal of Geophysics-Chinese Edition, 2015, 58(9): 3356–3369. (in Chinese). DOI:10.6038/cjg20150928. [23] CONSTABLE S C, PARKER R L, CONSTABLE C G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data [J]. Geophysics, 1987, 52(3): 289–300. DOI: 10.1190/1. 1442303. [24] JIANG Fei-bo, DAI Qian-wei, DONG Li. Nonlinear inversion of electrical resistivity imaging using pruning Bayesian neural networks [J]. Applied Geophysics, 2016, 13(2): 267–278. DOI: 10.1007/s11770-016-0561-1. [25] LIU Mei-ling, LIU Xiang-nan, WU Men-xin. Integrating spectral indices with environmental parameters for estimating heavy metal concentrations in rice using a dynamic fuzzy neural-network model [J]. Computers & Geosciences, 2011, 37(10): 1642–1652. DOI: 10.1016/ j.cageo.2011.03.009. [26] JIANG Fei-bo, DONG Li, DAI Qian-wei, DAVID C N. Using wavelet packet denoising and ANFIS networks based on COSFLA optimization for electrical resistivity imaging inversion [J]. Fuzzy Sets and Systems, 2018, 337: 93–112. DOI: 10.1016/j.fss. 2017.07.009. [27] LI Guang, TANG Jing-tian, XIAO Xiao, LI Jin, ZHU Hui-jie, ZHOU Cong, YAN Fa-bao. Near-source noise suppression of AMT by compressive sensing and mathematical morphology filtering [J]. Applied Geophysics, 2017, 14(4): 581–589. DOI: 10.1007/s11770-017-0645-6. [28] JIANG Fei-bo, DONG Li, DAI Qian-wei. Electrical resistivity imaging inversion: An ISFLA trained kernel principal component wavelet neural network approach [J]. Neural Networks, 2018, in press. DOI: 10.1016/j.neunet. 2018.04.012. (Edited by YANG Hua) 中文导读 基于二阶段CO-PSO最小构造反演的MT信号激电信息提取研究与CUDA实现 摘要:从大地电磁测深资料中提取激发极化信息,对深部矿产、油气资源的开发具有极为重要的现实意义。目前的IP信息提取方法多以线性反演方法为主,主要存在以下3个问题:1)依赖初始模型;2)容易陷入局部极值;3)多解性严重。考虑到IP信息提取的非线性和非凸性,本文提出了一种采用二阶段CO-PSO最小构造反演方法来提取MT信号中的激电信息。在该方法中,一方面,运用柯西振荡粒子群优化(CO-PSO)算法从MT数据中非线性提取激电信息,并使用CUDA架构进行并行实现;另一方面通过引入第二阶段反演过程,增强反演时极化率对观测数据的影响,同时为了解决反演中的多解性问题,将正则化参数应用于PSO算法的适应度函数。通过对不同地电模型下极化层位于不同地层的反演结果表明,该算法可以得到电阻率和极化率的光滑模型,其结果相对稳定,准确。加入噪声后的实验结果表明,该方法对高斯白噪声具有鲁棒性。与传统的PSO和GA算法相比,该算法具有更高的反演效率以及更好的反演效果。 关键词:柯西振荡粒子群优化;大地电磁测深;非线性反演;激电信息提取;CUDA Foundation item: Projects(41604117, 41204054) supported by the National Natural Science Foundation of China; Projects(20110490149, 2015M580700) supported by the Research Fund for the Doctoral Program of Higher Education, China; Project(2015zzts064) supported by the Fundamental Research Funds for the Central Universities, China; Project(16B147) supported by the Scientific Research Fund of Hunan Provincial Education Department, China Received date: 2017-02-20; Accepted date: 2017-05-10 Corresponding author: LI Di-quan, Associate Professor, PhD; Tel: +86–15802637512; Fax: +86–731–88876014; E-mail: 76399509@ qq.com; ORCID: 0000-0001-8435-4655 (7)
(7)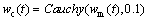 (8)
(8)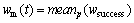 (9)
(9) (10)
(10)
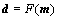 (11)
(11)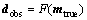 (12)
(12) (13)
(13)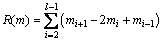 (14)
(14)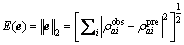 (15)
(15)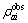
 is the observed apparent resistivity data;
is the observed apparent resistivity data; 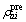 is the calculated apparent resistivity data for a given model obtained by forward mapping F with different mode parameters in a different inversion stage and can be calculated as follows:
is the calculated apparent resistivity data for a given model obtained by forward mapping F with different mode parameters in a different inversion stage and can be calculated as follows: (16)
(16)