J. Cent. South Univ. Technol. (2007)03-0425-06
DOI: 10.1007/s11771-007-0083-3
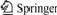
Expansive soil-structure interaction and its sensitive analysis
XIAO Hong-bin(肖宏彬)1,2, ZHANG Chun-shun(张春顺)1,2, HE Jie(何 杰)1, FAN Zhen-hui(范臻辉)2
(1. Institute of Geotechnical Engineering, Hunan University of Technology, Zhuzhou 412008, China;
2. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)
Abstract: Several groups of direct shear tests of Nanning expansive soil samples were carried out by improved direct shear apparatus. The results of the characteristics of the ultimate shear stress and residual shear stress at the interface of expansive soil-structure are presented as follows: linear relation can approximately reflect changes between the both shear stress and the three factors: vertical load, water content and dry density, just different degrees from each other; increasing the vertical load from 25 kPa to 100 kPa (up by 300%) can cause the average increase of ultimate shear stress from 58% (for samples with 1.61 g/cm3) to 80% (for samples with 1.76 g/cm3), and an close average increase of 180% for the residual shear stress; increasing the water content from 14.1% to 20.8% (up by 47.5%) can cause the average decrease of the ultimate shear stress from 40% (for samples with 25 kPa) to 80% (for samples with 100 kPa), and the average decrease from 25% (for samples with 25 kPa) to 30% (for samples with 100 kPa) for the residual shear stress; increasing the dry density from 1.61 g/cm3 to 1.76 g/cm3 (up by 9.3%) can cause the average increase of ultimate shear stress from 92% (for samples with 25 kPa) to 138% (for samples with 100 kPa), and an average increase of 4% for the residual shear stress. Sensitive analysis was further made to explain reasons causing the differences of the both shear stress induced by the three factors.
Key words: expansive soils; interface; direct shear friction test; ultimate shear stress; residual shear stress
1 Introduction
The problem of structure-soil interaction is always an important subject in geotechnical engineering. Many scholars have done a lot of studies on it and obtained some beneficial results. YIN et al[1]observed the distribution along a soil-concrete interface in direct shear test by some mini-periscopes clung to the bottom of the sample, suggesting a view of rigid-plastic deformation relationship; HU et al[2] carried out a series of soil-structure shear tests by an improved direct shear apparatus, to study the effect of different relative roughness on mechanical characteristics of interfaces. ZHANG et al[3] studied the slippage friction of the pile-soil interface, with following the time-related characteristics of the friction. CLOUGH et al[4] probed into the mechanics behavior of the concrete-soil interface by means of shear test, proved the hyperbolic relationship between shear stress and relative shear displacement. POTYONDY[5] used a strain-controlled and a stress-controlled shear apparatus to study the mechanics characteristics of the interfaces between various soils and architecture materials. Different models were proposed to simulate and analyze the behavior of soil and structure interaction, and the results are
practically applicable[6-9].
Expansive soil is a special soil that is very sensitive to the change of water content. The introduction of water makes it volumetrically swell, softening the soil strength, while the loss of water makes it volumetrically shrink, hardening the soil strength or even producing cracks. Many factors, such as water content, dry density and vertical load have great impact on the soil behavior, affecting load transfer characteristics for piles in expansive soil. XIAO et al[10-11] found the approximate linear relationship between each above-mentioned factor and expansive soil deformation, respectively, through a lot experimental studies. The purpose of this study is to probe into the change laws of the mechanical behavior of expansive soil-structure interface under those factors changes, providing basis to study the pile-expansive soil interaction.
2 Shear test of structure-expansive soil interface
2.1 Introduction and preparation of samples
The expansive soil sample from Nanning is alluvial or diluvial soil, which is grey-white and has medium expansivity. The basic physical and mechanical characteristics of the expansive soil is listed in Table 1.
Table 1 Physical and mechanical characteristics of expansive soil

To systematically analyze the effect of expansive soil’s characteristics on mechanics of the interface, 32 pieces of samples were prepared as follows: four groups (4 samples in each group of samples) with water content 14.1%, 15.8%, 17.8%, and 20.8%, respectively and the samples’ dry density is 1.61 g/cm3; four groups (4 samples in each group of samples) with dry density 1.61, 1.67, 1.71, 1.76 g/cm3, respectively and the samples’ water content is 15.8%. The sample-preparation procedure is described as follows[12]: (1) let the grinding air-dried soil sample run through a 2 mm sieve and mix it enough; (2) measure the water content after being air dried, and calculate the required amount of water for the soil with certain water content; (3) spray estimated amount of water on the soil, put the mixed sample into the plastic bag, fasten the neck of the bag, and put it in the wet-keeping jar for 24 h in order to ensure the water in the samples is well-proportioned; (4) measure water content (105-110 ℃, 8 h) of the samples by using the oven drying method and calculate the mass of the cutting ring samples with reference to the required dry density; and (5) put two back-to-back cutting rings on a table with a even pad, pour the measured sample into the cutting rings, place a metallic block on the above cutting ring whose one-dimensional diameter is equal to the inside one of the cutting ring and height equal to that of the cutting ring, and then strike the block into the cutting ring till the two are at the same level.
2.2 Shear friction test
The improved shear apparatus is shown in Fig.1. Replace the low porous stone of the original one with a concrete block in order to simulate a concrete pile. Make sure the surface of the concrete block and the top of the low shear box are at the same level.

Fig.1 Sketch of experimental instrument
In the test, the shear velocity is set to be 0.02 mm/ min, with the vertical loads of 25, 50, 75 and 100 kPa, respectively. During the shear process, the shear stress and relative shear displacement are automatically recoded by a computer-data-collecting- handling system (Style: TSW-3; produced by Nanjing Electric Power Automation Equipment Factory Ministry of Energy, China). And when the shear stress is around constant or the relative shear deformation is up to 4 mm, stop the test.
3 Result analysis
3.1 Effect of vertical loads on ultimate and residual shear stress
The result of the relationship between vertical loads and ultimate shear stress of the interface is shown in Fig.2. And the relation of residual shear stress at the interface to the vertical loads is given in Fig.3.

Fig.2 Relationship between vertical load and ultimate shear stress
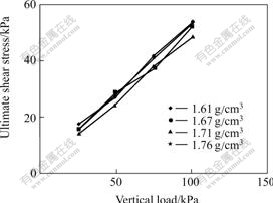
Fig.3 Relationship between vertical load and residue shear stress
Figs.2 and 3 show the changes of shear stress of the samples with water content 15.8% , and dry density 1.61, 1.67, 1.71, and 1.76 g/cm3, respectively, under different vertical loads. The linear regression was made to fit the curves in the two figures and the degree of agreement |R| exceeds 0.96, a very satisfactory result. Thus, a simple linear function can be adopted to describe the relations of vertical loads to ultimate shear stress as well as residual shear stress:
τs=aP+b (1)
τ1=a′P+b′ (2)
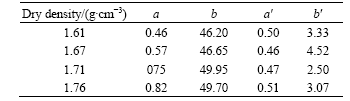
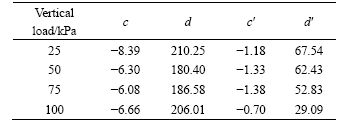
where a, b, a′, and b′ are constants, see Table 2.
Table 2 Parameters of soil-concrete interface for samples with W0=15.8%
Statistically analyzing the data in Fig.2 and Fig.3, it is noted that when dry density is given, increasing the vertical load from 25 kPa to 100 kPa, the effect on ultimate shear stress and residual shear stress is different. For ultimate shear stress of the samples from 1.61 g/cm3 to1.76 g/cm3, an average increment is from 58% to 80%; under the same condition, the increments of residual shear stress of all samples are close, an average increment of 180%. Apparently, vertical loads contribute more to the increase of the residual shear stress than the ultimate shear stress.
Besides, in Fig.3, the cohesion cr is very small for the residual shear stress, nearly to be zero. So the strength of the residual shear stress mainly depends on residual internal friction angle φr. The reason may be explained from two aspects: on the one hand, flat grains at the shearing interface are easily highly ordered arranged in the direction of shearing; on the other hand, water may assemble at the shearing interface, softening the strength of the interface[13]. As seen in Table 2, cr of the residual shear stress obtained from the 4 groups of samples are only among 2.50 and 4.52, while among 46.20 and 49.95 for the corresponding cohesion of the ultimate shear stress, much higher than that of residual shear stress.
3.2 Effect of water content on ultimate and residual shear stress
Figs.4 and 5 show, respectively, the results obtained in the experiments reflecting the relationship between water content and ultimate shear stress, and the relation of water content to residual shear stress.
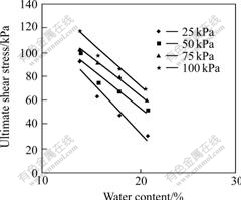
Fig.4 Relationship between water content and ultimate shear stress

Fig.5 Relationship between water content and residual shear stress
The water contents of the samples in Figs.4 and 5 are 14.1%, 15.8%, 17.8% and 20.8%, respectively. It is easy to tell approximate linear relations of water content to ultimate shear stress or residual shear stress. An regression analysis displays a very high degree of linear agreement, |R|>0.95. Besides, both ultimate shear stress and residual shear stress decrease with the increase of water content. Similarly, simple linear functions would be used to fit each linear relation of the both shear stresses to water content:
τs=cw+d (3)
τ1=c′w+d′ (4)
where c, d, c′, and d′ are constants (see Table 3).
Table 3 Parameters of soil-concrete interface for samples with ρ0=1.61 g/cm3
Besides, slopes of the linear curves in Fig.4 are apparently much greater than those of curves in Fig.5, viz, changes of water content contribute much more impact on changes of ultimate shear stress than those of residual shear stress. Statistic analysis of the four groups of test data shows that with the water content increases from 14.1% to 20.8%, an increment of 47.5%, the ultimate shear stress decreases by 40% at least (for samples with 25 kPa) while 80% at most (for samples with 100 kPa); as for the corresponding residual shear stress, 25% at least (for samples with 25 kPa) while only 30% at most (for samples with 100 kPa). This means water content has much more effect on ultimate shear stress than that of residual shear stress.
3.3 Effect of dry density on ultimate and residual shear stress
Fig.6 presents the relationship between dry density and ultimate shear stress at the soil-concrete interface and Fig.7 shows the relationship between dry density and residual shear stress.
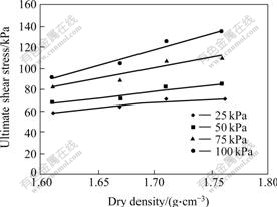
Fig.6 Relationship between dry density and ultimate shear stress

Fig.7 Relationship between dry density and residue shear stress
The samples are under vertical loads of 25, 50, 75, and 100 kPa. The changes of the shear stress with the changes of dry densities are presented in Figs.6 and 7, respectively. It can be easily found in Fig.6 that the ultimate shear stress increases with the increase of dry densities. Statistically analysis shows that increasing the dry density from 1.61 g/cm3 to 1.76 g/cm3 (up by 9.3%) can cause the average increase of ultimate shear stress from 92% (for samples with 25kPa) to 138% (for samples with 100kPa). A regression analysis of the data was performed, obtaining a high degree of linear agreement, |R|>0.97.
As for Fig.7, dry density has little effect on residual shear stress, which may seems to be ignored. But the increment of dry density in this experiment is very small, only 0.05 g/cm3 for two neighboring samples, so the increment of residual shear stress induced by the increase of dry density seems very small. Actually, in this test, for a certain vertical load, when dry density increases from 1.61 g/cm3 to 1.76 g/cm3, an increment of 9.3%, the average increment of residual shear stress is up to 4%.
Note that soils in nature are residual soils. Their changes of dry density are stable, among 1.6 g/cm3 and 1.7 g/cm3. So the very small changes of residual shear stress induced by dry density may be neglected in practical engineering.
Similarly, simple linear functions can describe the relations of dry density to ultimate shear stress and to residual shear stress:
τs=eρ+f (5)
τs=e′ρ+f′ (6)
where e, e′, f, f′ are constants (see Table 4).
Table 4 Parameters of soil-concrete interface of sample with ρ0=1.61 g/cm3

4 Sensitive analysis of effects of different factors on ultimate and residual shear stress
Fig.8 presents the most sensitive factor to the changes of ultimate and residual shear stress. For ultimate shear stress, the most one is dry density, then water content, and the last one is vertical load; while for residual shear stress, the most one is water content, then vertical load, and dry density at least. Meanwhile, Fig.8 shows that water content and dry density contribute much more impact on ultimate shear stress than that of residual shear stress, while changes of vertical loads have more influences on residual shear stress than that of ultimate shear stress, which also means the difference between ultimate and residual shear stress in their beginning and developing laws.
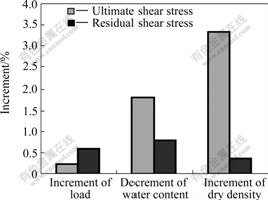
Fig.8 Effects of different aspects on ultimate shear stress and residue shear stress
LIU[13] mentioned that shear strength of expansive soil depends on friction induced by the relative displacement among grains and grains’ agglutination. So increasing vertical loads, with no doubt, will increase the friction at the soil-concrete interface and hereby enhance ultimate shear stress as well as residual shear stress. In Ref.[1], it is proved that the deformation at the interface is composed of two parts: one is basic soil deformation, the other is damage deformation, as seen in Fig.9. Apparently, the ultimate shear stress is produced in the process of the basic deformation while residual shear stress the damage deformation after the basic one. It is harder for the beginning of the basic deformation, which needs more shear force and after that, it is easier to begin and develop the damage deformation, much less shear force needed. That’s why ultimate shear stress is always greater than residual shear stress.
As for the reason why residual shear stress is more sensitive to the increase of vertical loads, the author believes the difference of interface is responsible for it. The process of the basic soil deformation is the interaction between the concrete and expansive soil while the damage deformation is the interaction between the soil clinging to the concrete and the residual soil sample, viz, the soil-soil interaction. That might be proved by observing the concrete sample clung to soil after the test. Clearly, the friction between soil and concrete is induced purely by a rigid movement while the friction between soil and soil is induced by the relative displacement among grains and grains’ agglutination caused by embedding effect among grains, much greater than that of soil-concrete interface. So the increase of vertical loads contributes more impact on residual shear stress.

Fig.9 Deformation mode at interface
The reduction of water content and the increase of dry density cause the shear stresses to increase, which is easy to understand, for essentially increasing the coarseness of an interface will enhance the friction at the interface. However, as shown in Fig.8, the two factors’ impacts on the both shear stresses are different. Explanation may be like this: water would aggregate at an interface during the shearing process, evaluating the water content of the interface, thus softening the interface’s strength[13]. During the process of the basic soil deformation, the aggregation of water at the interface only impacts on soil’s strength of the soil sample while in damage deformation, the aggregation of water impacts on both soil’s strength for clinging soil at the concrete surface as well as the soil strength of the residual soil block, around two times softening than that of the basic soil deformation. So, when water content decreases, the increment of ultimate shear stress may be twice as great as that of residual shear stress, which is agreeable to the presentation in Fig.8.
As for the different effects of dry density on the both shear stresses, it could be explained as follows. On the one hand, the increase of dry density enhances the coarseness of the soil-concrete interface, increasing the friction of the interface. Thus, greater shear forces are required to begin the basic soil deformation; on the other hand, increasing dry density would cause thinner soil layer clinging to the concrete surface during the damage deformation, thus the grains’ agglutination caused by embedding effect among grains may increase a little or very little. At this time, the strength of the damage deformation largely depends on soil-soil friction, much less than that of soil-concrete friction. So, ultimate shear stress is more sensitive to dry density than residual shear stress.
5 Conclusions
1) Ultimate and residual shear stresses are, respectively, linear relations with vertical loads, viz, the both shear stresses increase with the increase of vertical loads; the increase of vertical loads contribute more to the increase of residual shear stress than that of ultimate one.
2) Ultimate shear stress at the interface is approximately linear relation with water content, viz, decreasing with the increase of water content, so does residual shear stress; the change of ultimate shear stress is much more sensitive to the change of water content, viz, water content has much more influence on ultimate shear stress than residual shear stress.
3) Both ultimate and residual shear stresses have approximately linear relation with dry density, viz, the shear stresses increase with the increase of dry density; ultimate shear stress is much more sensitive to changes of dry density, viz, the effect of dry density on ultimate shear stress is much greater than that of residual shear stress.
4) The differences of effects of vertical load, water content and dry density on ultimate and residual shear stress indicate the differences of beginning and development of the both shear stresses, for which two deformation modes induced by two different interfaces in shear deformation are responsible essentially. One is the basic soil deformation at soil-concrete interface; the other is the damage deformation at the soil-soil interface.
References
[1] YIN Zong-ze, ZHU Hong, XU Guo-hua. Numerical simulation of the deformation in the interface between soil and structural material[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3): 14-22. (in Chinese)
[2] HU Li-ming, PU Jia-liu. Experimantal study on mechnial characteristics of soil-structure interface[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 431-435. (in Chinese)
[3] ZHANG Ming-yi, DENG An-fu. Experimental study on sliding friction between pile and soil[J]. Rock and Soil Mechanics, 2002, 23(2): 246-249. (in Chinese)
[4] CLOUGH G W, DUNCAN J M. Finite element analysis of retaining wall behavior[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1971, 97(12): 1657-1672.
[5] POTYONDY J G. Skin friction between various soils and construction material[J]. Geotechnique, 1961, 11(4): 339-353.
[6] XIONG Hui, ZOU Yin-sheng, TIAN Jun. Dynamic finite-element analysis of pile-soil-structure system considering thin-layer contact element[J]. Journal of Hunan University: Natural Sciences, 2004, 31(1): 59-63. (in Chinese)
[7] LUAN Mao-tian, WU Ya-jun. A nonlinear elasto-perfectly plastic model of interface element for soil-structure interaction and its applications[J]. Rock and Soil Mechanics, 2004, 25(4): 507-513. (in Chinese)
[8] DU Cheng-bin, REN Qing-wen. A new three-dimensional nonlinear interface element for modeling joints[J]. Journal of Southeast Unversity: Natural Science Edition, 2001, 31(4): 92-96. (in Chinese)
[9] ZHANG Dong-ji, LU Ting-hao. Establishment and application of an interface model between soil and structure[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(6): 62-66. (in Chinese)
[10] XIAO Hong-bin, LIU Jie, WANG Yong-he. Experimental and theoretic studies on the law of load transfer of large-diameter pile[J]. Geotechnical Engineering Technique, 2003(1): 47-50. (in Chinese)
[11] XIAO Hong-bing, FAN Zhen-hui, WANG Yong-he. Experimental study on swelling laws of expansive soil with water-addition in one-dimension[C]// Proceedings of Eighth National Symposium on Foundation Improvement. Hefei: Hefei University of Technology Press, 2004. (in Chinese)
[12] The Ministry of Water Resources of the PRC. SL237-1999. Test Methods of Soils[S]. Beijing: China Water Power Press, 1999. (in Chinese)
[13] LIU Te-hong. Expansive Problems in Engineering Practice[M]. Beijing: China Architecture and Building Press, 1998. (in Chinese)
(Edited by YUAN Sai-qian)
Foundation item: Projects(50378097; 50678177) supported by the National Natural Science Foundation of China; Project (01JJY3043) supported by the Natural Science Foundation of Hunan Province, China
Received date: 2006-10-24; Accepted date: 2006-12-27
Corresponding author: ZHANG Chun-shun, Doctoral candidate; Tel: +86-13873304348; E-mail: marshell2004@163.com