J. Cent. South Univ. (2017) 24: 2145-2153

DOI: https://doi.org/10.1007/s11771-017-3623-5

Bending tests and finite element analysis of lipped channels with complex edge stiffeners and web stiffeners

WANG Chun-gang(王春刚), ZHANG Zhuang-nan(张壮南), JIA Lian-guang(贾连光), YU Xin-yong(于欣永)

School of Civil Engineering, Shenyang Jianzhu University, Shenyang 110168, China

Central South University Press and Springer-Verlag GmbH Germany 2017

Abstract: In order to study the bearing capacity and stability behavior of cold-formed steel flexural members with complicated sections, a total of 12 specimens divided into 6 groups were tested, including 3 groups of pure bending tests and non-pure bending tests each. There were three types of sections considered in this investigation, including channels with complex edge stiffeners (called B1-section), Σ section with complex edge stiffeners (called B2-section), and channels with complex edge stiffeners and V-type web stiffeners (called B3-section). Local buckling, distortional buckling and interaction buckling between them were observed in tests. The experimental results indicate that the bending strengths of B2-section specimens were the largest of these three types of specimens under the same conditions. It is found that the bending strength of B2-section specimens was increased by 6.47% for pure bending state and 8.12% for non-pure bending state, compared with that of B1-section specimens. Bending strength of B3-section specimens was almost the same with that of B1-section specimens under pure bending, but a little smaller than that of B1-section under non-pure bending state. It is also shown that B2-section specimens have better plastic deformation behavior than the other two sections. In addition, a non-linear finite element model was presented and verified against tests. The finite element analysis results agree well with experimental bending strength and failure modes.

Key words: cold-formed steel; channels with complex edge stiffeners; web stiffeners; bending strength; buckling

1 Introduction

Cold-formed steel structural members are widely used in civil construction around the world. They are often made of thin material, and singly symmetric open sections are commonly used in practice. Local buckling and distortional buckling must be considered as an essential part of member design, which can be ignored in compact members [1-3]. Three of the most common flexural members used in these applications are the plain C, the Z (typically with sloping lips), and a variety of generally “hat-shaped” sections [4, 5]. All of these conventional sections have been in regular use for many years. In recent years, cross-section innovation has begun to take greater advantage of manufacturing technology, and begun to seriously push the boundaries of available design methods [6-8]. Ultra-thin material, high-strength and complicated cross-section is the developing trend of cold-formed thin-walled steel members. Therefore, it is necessary to carry out experimental and numerical research on bearing capacity and buckling behavior of flexural members, especially for those with novel sections.

Longitudinal edge stiffener is a crucial component of thin-walled open sections, which influences the bearing capacity and stability behavior of members in bending seriously. Complex edge stiffeners contained additional return lips at the free edge can improve the stability and enhance the bending strength of the sections [9]. On the other hand, buckling stress of the elements also can be increased by intermediate stiffeners [10]. It leads to an economic design. In the past, researches on flexural members generally focused on those with simple edge stiffeners [11-13]. Investigation on bending behavior of web-stiffened channels with complex edge stiffeners is scarce. Furthermore, existing tests of C- and Z-section flexural members are mainly subjected to pure bending. Members under moment gradients need to be studied more.

Three types of complicated sections bending tests and finite element analysis (FEA) focused on complex edge stiffeners and web stiffeners were reported in this work. Both pure bending and non-pure bending conditions were performed. Considering the bending strength of flexural member may decrease obviously if lateral-torsional global buckling occurred, braces are usually used to restrain lateral-torsional buckling in practice [14]. We mainly deal with local buckling, distortional buckling and their interactive buckling in this work.

2 Experimental

A total of 12 simply supported flexural specimens that divided into 6 groups were tested, including 3 groups of pure bending tests and non-pure bending tests each. Three types of sections considered in the tests are as follows, channels with complex edge stiffeners (Fig. 1(a), called B1-section), Σ section with complex edge stiffeners (Fig. 1(b), called B2-section), and channels with complex edge stiffeners and V-type web stiffeners (Fig. 1(c), called B3-section).

2.1 Test specimens

Geometric parameters of the specimens are shown in Fig. 1. The nominal metal thickness is 2.0 mm, and all the geometrical sizes below were defined by surface outline. The nominal height of the web is 238 mm, with sub-height of the web H₁= H₂=60 mm, H₃=90 mm and H₁=H₂=105 mm for B2- and B3-section, respectively. The nominal width of the flange is 100 mm, the lip is 35 mm and the rear lip is 20 mm. For B2- and B3-section, the nominal width of the intermediate stiffener is 20 mm, and the angel between the stiffener and the web is 135°. The rounded inside corner radius is equal to the metal thickness. Two lengths of the specimens were designed, i.e. L=1930 mm for pure bending tests, and L=1330 mm for non-pure bending tests. Each specimen was manufactured by brake forming and double processed. Two identical specimens were arranged in one group, so that there were 6 groups of tests.

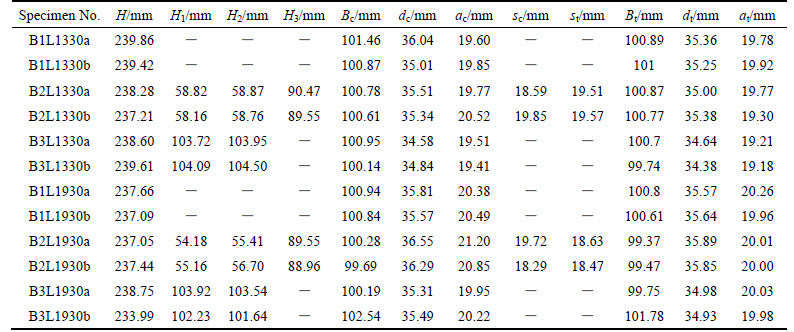
The section dimensions were measured at the mid-length and both ends by vernier caliper before tests. The actual sizes were defined by the average of the three measured results and shown in Table 1. The first column of Table 1 is the specimen numbering, which is defined as follows. B1, B2 and B3 refer to the three types of sections respectively; letter L and the number followed by refer to the length of the specimen; the last letter a or b refer to the sequence number of the same specimens.

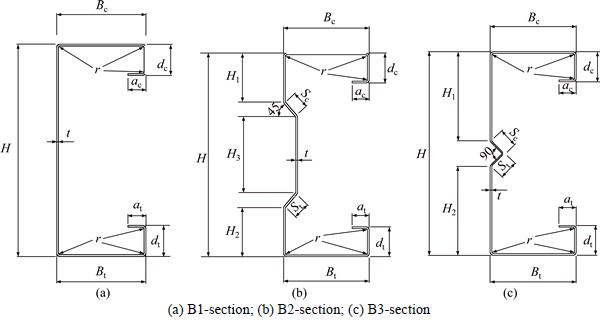
Fig. 1 Cross section and definition of symbols:

Table 1 Actual dimensions of specimens

2.2 Material properties

The material properties were determined by tensile coupon tests according to the Chinese Standard (GB/T 228–2002) [15]. A total of nine longitudinal coupons were tested to measure the metal properties. For each type of section, three coupons were taken from the finished specimens. One was from the web and the other two were from compression and tension flange, respectively. No coupon was taken from the corner zone. Although both the significant residual stress and the increase of yield strength due to cold-forming exist in corner region, they are going in the opposite sense on instability behavior and tend to compensate each other [16]. So, the cold working effects and residual stress at section corners were negligible when describing the material properties of the overall cross section. The average results of coupon tests shown in Table 2 were taken as the material properties for all specimens.

2.3 Initial geometric imperfections

Local, distortional and overall imperfections of the research spans of all specimens were measured before tests. The measurement used in Ref. [17] was consulted. For measure convenience, the research spans of specimens were meshed into several parts and marked along the length and the width. Then dial gauges were used to measure the imperfections at griddings. Local imperfections of the web (Δ_w) and the compression flange (Δ_f), distortional imperfections at the intersection of the compression flange and the lip (Δ_fl), overall flexural imperfections on major (Δ_x) and minor (Δ_y) axis were measured. Because the tension flange was not sensitive to imperfections, the local and distortional imperfections of it were not measured. All amplitude values and those to thickness ratios of the above imperfections are listed in Table 3.

2.4 Test setup and gauge arrangement

The schematic diagrams of pure bending and non- pure bending tests are shown in Fig. 2. Both bending states have the equal research span length of 600 mm. For pure bending test, the constant moment span is between two loading points (Fig. 2(a)). For non-pure bending test, research span is the shear span without the steel cover plate bolted on the compression flanges (Fig. 2(b)). In order to prevent the lateral-torsional buckling, the same two specimens were bolted (M16 bolts) together back-to-back through the load transfer devices (which has sufficient stiffness) at loading points and supported devices at both ends to provide lateral supports (see Fig. 3). In addition, the compression flanges of two specimens except the research span were covered by steel plates (thickness is 6 mm) and bolted together with spacing 140 mm. A 500 kN capacity hydraulic jack was used for loading. The photo of pure bending test setup is shown in Fig. 4. For non-pure bending test, specimens were loaded at mid-length. The connection modes of the specimens and steel cover plates were the same with that in pure bending test.

Table 2 Results of coupon tests

Table 3 Amplitude initial imperfections of specimens

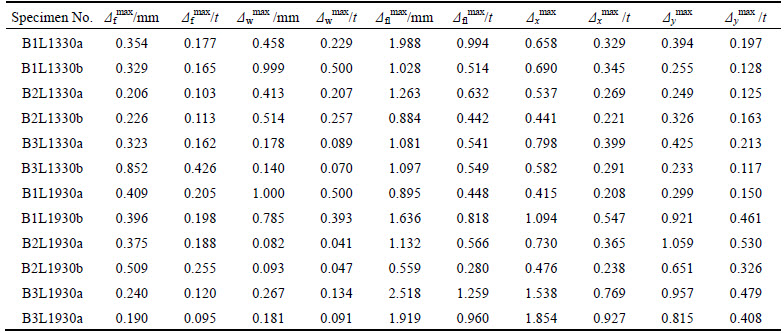
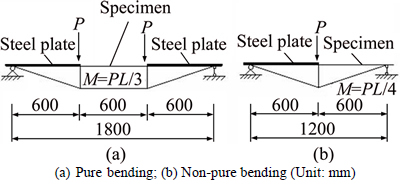
Fig. 2 Schematic diagrams of bending tests:

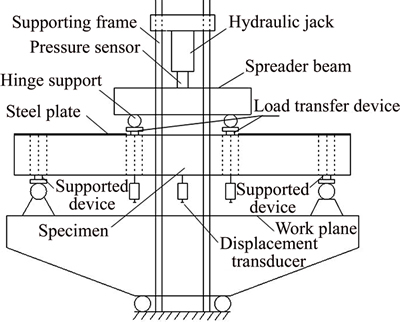
Fig. 3 Schematic view of pure bending tests rig

Fig. 4 Pure bending tests setup

Displacement transducers were located at the web/tension flange junction of each specimen to measure the vertical displacement at mid-span and the loading points (see Fig. 3). All strain gauges were arranged on compression flange and complex edge stiffeners at mid-span section of each specimen to monitor the stress distribution, as shown in Fig. 5. The strain gauges were numbered from 1 to 12.

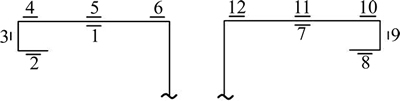
Fig. 5 Strain gauges arrangement

3 Test results

3.1 Pure bending test results

All specimens failed in combined local (L) and distortional (D) bucking modes in pure bending test. The typical failure modes are illustrated in Fig. 6. There is no overall buckling and lateral displacement observed in tests. The peak values of local and distortional buckling usually occur on the web and compression flange near the mid-span for B1-section (Fig. 6(a)) and near one loading point for the other two sections (Figs. 6(b) and (c)). This phenomenon may be related to the longitudinal web stiffeners, which increases the web bending stiffness. Local buckling happened on compression flange first. When the amplitude of local buckling is visible, distortional bucking appears and would develop the local and distortional interactive buckling. Compared with the deformation of B1-section pure bending specimens, it is found that the local buckling region on the web of B2-and B3-section pure bending specimen is smaller than that of B1-secion specimen influenced by web stiffeners.

Fig. 6 Failure modes of pure bending tests:

The pure bending test results are listed in Table 4. It is shown that the bending strength of B2-section is the largest among these three types of sections. It is 6.47% higher than that of B1-section. The difference of bending strength between them is affected by the stiffener on the web of B2-secion. The longitudinal web stiffeners of B2-secion could reduce the compression web width-to-thickness ratio effectively and enhance the stability capacity of members. Whereas, bending strength of B3-section is almost the same with that of B1-section, because the V-type stiffener located at the middle of the web (the neutral axis of the section) has little effects on bending strength of the member.

The load-vertical displacement curves at the mid-span of the pure bending tests are shown in Fig. 7(a). It is shown that the curves of B1- and B3-section have a shorter plastic stage and dropped immediately after the ultimate loads compared with B2-section. It indicates that the pure bending specimens of B2-section have better plastic deformation performance than the other two sections.

3.2 Non-pure bending test results

Figure 8 shows the failure modes of non-pure bending tests. The local (L) and distortional (D) interactive bucking also appears in tests. But the peak value of local and distortional bucking emerges on the web and compression flange near the loading point for all these three sections. The foremost local buckling occurs on the compression flange and it also appears before distortional bucking. Compared with the deformation of B1-section, the local buckling region on the web of B2-and B3-section non-pure bending specimen is smaller than that of B1-secion specimen influenced by web stiffeners.

The non-pure bending test results are shown in Table 5. It is shown that the bending strength of B2-section is also the largest among these three types of sections. It is 8.12% higher than that of B1-section. Whereas, bending strength of B3-section is a little smaller than that of B1-section. V-type stiffener in the middle of the web may result in a detrimental effect on bending and shear combination.

The load-vertical displacement curves at the loading point of the non-pure bending tests are shown in Fig. 7(b). It is similar to the pure bending tests that the curves of B1- and B3-section have a shorter plastic stage and decline relatively immediately during the post- ultimate stage compared with B2-section. The non-pure bending specimens of B2-section also have better plastic deformation behavior than the other two sections.

Table 4 Comparison of tests and FEA results of pure bending specimens

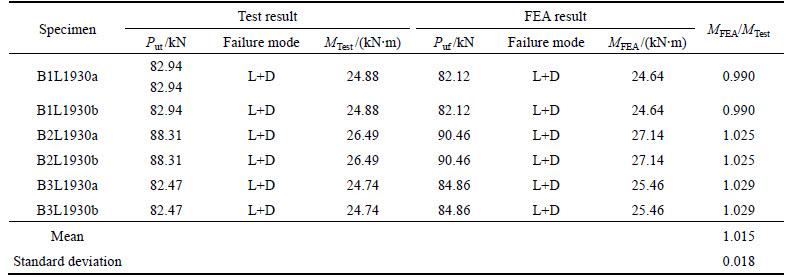
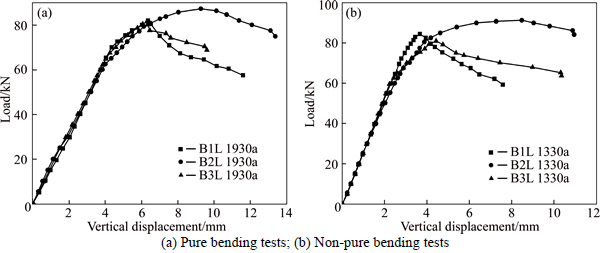
Fig. 7 Load-vertical displacement curves:

Fig. 8 Failure modes of pure bending tests:

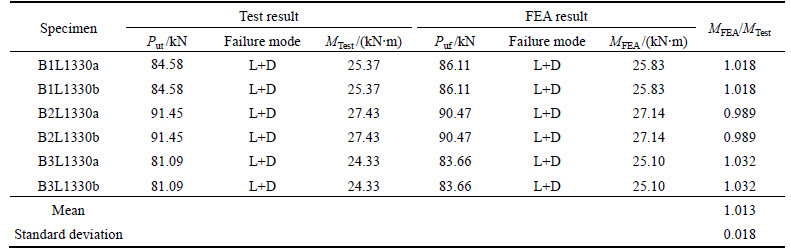
Table 5 Comparison of tests and FEA results of non-pure bending specimens

4 Finite element analysis

The finite element program ANSYS was used to develop the finite element model to simulate the bending strength and stability behavior of cold-formed steel flexural members with complicated sections mentioned in experimental program. An eigenvalue elastic buckling analysis was first conducted to establish probable buckling modes (eigenmodes) of the specimens. Then, a non-linear buckling analysis was carried out using the arc-length method to predict the bending strength, failure modes and vertical displacements at mid-span or loading point of the specimens.

4.1 Finite element model

Regarding the finite element model, element SHELL181 was selected to simulate the specimen, steel cover plate, load transfer device and supported device in the tests. It is a four-node three-dimensional quadrilateral element with six degree of freedom on each node. The elastic property of shell element was used for eigenvalue buckling analysis, and plastic property which allowed that large deflection behavior was used for non-linear buckling analysis.

The size of element influences the precision of FEA results. By varying sizes of the elements, it is found that the suitable element size is about 20 mm×(8-20) mm×12 mm for the complex edge stiffeners, and 20 mm×16 mm for the flange and web. The boundary conditions of the specimens are simply supported at the bottom of the supported devices.

4.2 Initial imperfections and material modeling

Geometric imperfection and material nonlinearity are considered in FEA. The eigenmode 1 scaled by a factor was used to obtain the geometric imperfection for the non-linear buckling analysis. The amplitude of the geometric imperfection measured before tests (Table 3) is used to specify the factor. The material behavior is approximately described by a bilinear stress-strain curve. The initial slope of the curve is taken as the elastic modulus (E) of the material. At the yield strength (f_y) of the material, the curve was turned along the second slope defined by the tangent modulus (2% of the elastic modulus). All material properties are input as measured values from the coupon tests (Table 2). Both the increase of material yield strength by cold-forming process and the influence of residual stress are ignored in the analysis.

4.3 Comparison with experimental results

The FEA results and its comparison with tests are given in Table 4 for pure bending specimens and Table 5 for non-pure bending specimens. Their failure deformation and load vs vertical displacement curves are also compared with each other in Figs. 9 and 10. It is found that the average difference of bending strength between FEA and tests is only 1.5% and 1.3% for pure and non-pure bending specimens, respectively. Furthermore, both failure modes and load vs vertical displacement curves predicted by FEA agree well with the experimental results. Therefore, the stability behavior of cold-formed thin-walled steel flexural members could be accurately simulated by the finite element model presented in this work. It could be used for the future parameter study to predict the performance of the above members.

4.4 Stress distribution analysis

The Von Mises stress distribution is also analyzed by FEA, which could not be observed from tests. Typical stress distribution nephograms of pure bending and non-pure bending members under ultimate loading condition are shown in Fig. 11. From the figure we can see that the maximum compressive stress on pure bending members usually emerged on compressive flange along the pure bending segment. But for non-pure bending members, the maximum compressive stress appears on the juncture of compressive flange and web which is close to the loading point. The longitudinal web stiffeners of B2-secion reduced the width-to-thickness ratio of compressive web, which enhances bending and shearing stiffness of member and changes stress distribution also, especially on the web. The maximum compressive stress of B2-section specimens is larger than that of B1-section specimens under whether pure bending or non-pure bending states.

Fig. 9 Comparison of tests (a, b) and FEA (a′, b′) failure deformation: (a, a′) B1L1930b; (b, b′) B1L1330a

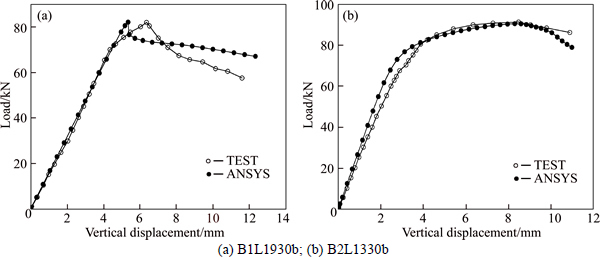
Fig. 10 Comparison of tests and FEA load-vertical displacement curves:

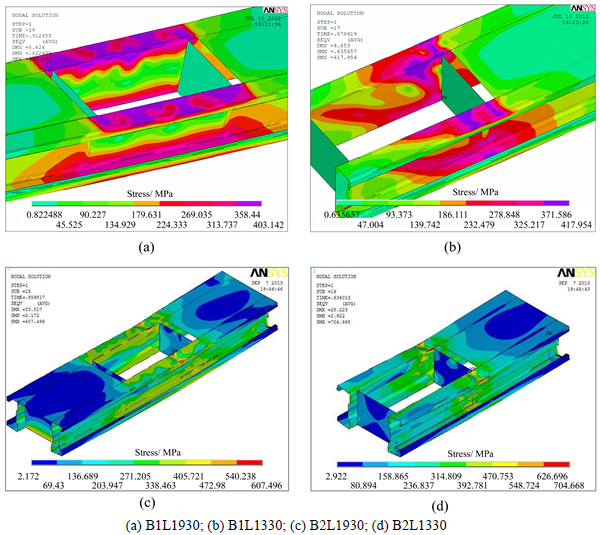
Fig. 11 Stress distribution nephograms:

5 Conclusions

1) Local buckling, distortional buckling and interaction buckling between them are observed in both pure bending and non-pure bending tests. There is no lateral-torsional buckling occurred during the tests. The tests setup presented in this work could restrain the global buckling of flexural members effectively.

2) The longitudinal web stiffeners of B2-secion could reduce the compression web width-to-thickness ratio effectively and enhance the stability capacity of members. The bending strengths of B2-section specimens are the largest of these three types of specimens under any pure bending or non-pure bending states. Moreover, the B2-section specimens have better plastic deformation behavior than the other two sections.

3) The bending strength of B2-section specimens is increased by 6.47% for pure bending state and 8.12% for non-pure bending state, compared with that of B1-section specimens. Bending strength of B3-section specimens is almost the same with that of B1-section specimens under pure bending, but a little smaller than that of B1-section under non-pure bending state.

4) The tests can be simulated exactly by the finite element model presented in this work. The FEA predictions are generally in good agreement with the experimental bending strength, failure modes and deformation behavior. So that, it seems that the parameter study can be carried out by the FEA to investigate the static behavior of these kinds of members.

References

[1] Hancock G J. Design for distortional buckling of flexural members [J]. Thin-Walled Structures, 1997, 27(1): 3-12.

[2] YU C, SCHAFER B W. Local buckling tests on cold-formed steel beams [J]. Journal of Structural Engineering, 2003, 129(12): 1596- 1606.

[3] YU C, SCHAFER B W. Distortional buckling tests on cold-formed steel members in bending [J]. Journal of Structural Engineering, 2006, 132(4): 515-528.

[4] HANCOCK G J. Cold-formed steel structures [J]. Journal of Constructional Steel Research, 2003, 59(4): 473-487.

[5] RONDAL J. Cold formed steel members and structures: General Report [J]. Journal of Constructional Steel Research, 2000, 55(1–3): 155-158.

[6] SCHAFER B W. Cold-formed steel structures around the word—A review of recent advances in applications, analysis and design [J]. Steel Construction, 2011, 4(3): 1-9.

[7] BAMAGA S O, TAHIR M M, TAN T C, MOHAMMAD S, YAHYA N, SALEH A L, MUSTAFFAR M, OSMAN M H, RAHMAN A B A. Feasibility of developing composite action between concrete and cold-formed steel beam [J]. Journal of Central South University, 2013, 20(12): 3689-3696.

[8] MACDONALD M, HEIYANTUDUWA M A, RHODES J. Recent developments in the design of cold-formed steel members and structures [J]. Thin-Walled Structures, 2008, 46(7–9): 1047-1053.

[9] Schafer B W, Sarawit A, Pekoz T. Complex edge stiffeners for thin-walled members [J]. Journal of Structural Engineering, 2006, 132(2): 212-226.

[10] PHAM C H, HANCOCK G J. Experimental investigation and direct strength design of high-strength, complex c-sections in pure bending [J]. Journal of Structural Engineering, 2013, 139(11): 1842-1852.

[11] PHAM C H, HANCOCK G J. Direct strength design of cold-formed purlins [J]. Journal of Structural Engineering, 2009, 135(3): 229-238.

[12] SCHAFER B W, LI Z, MOEN C D. Computational modeling of cold-formed steel [J]. Thin-Walled Structures, 2010, 48(10, 11): 752-762.

[13] MOEN C D, SCHUDLICH A, HEYDEN A V D. Experiments on cold-formed steel c-section joists with unstiffened web holes [J]. Journal of Structural Engineering, 2013, 139(5): 695-704.

[14] SCHAFER B W, PEKOZ T. Laterally braced cold-formed steel flexural members with edge stiffened flanges [J]. Journal of Structural Engineering, 1999, 125(2): 118-127.

[15] GB/T228–2002. Chinese standard for metallic materials-tensile testing at ambient temperature [S] 2002. (in Chinese)

[16] Dubina D, Ungureany V. Effect of imperfections on numerical simulation of instability behavior of cold-formed steel specimens [J]. Thin-Walled Structures, 2002, 40(3): 239-262.

[17] WANG Chun-gang, ZHANG Zhuang-nan, ZHAO Da-qian, LIU Qing-qing. Compression tests and numerical analysis of web-stiffened channels with complex edge stiffeners [J]. Journal of Constructional Steel Research, 2016, 116(1): 29-39.

(Edited by FANG Jing-hua)

Cite this article as: WANG Chun-gang, ZHANG Zhuang-nan, JIA Lian-guang, YU Xin-yong. Bending tests and finite element analysis of lipped channels with complex edge stiffeners and web stiffeners [J]. Journal of Central South University, 2017, 24(9): 2145–2153. DOI:https://doi.org/10.1007/s11771-017-3623-5.

Foundation item: Project(51008200) supported by the National Natural Science Foundation of China; Project(2015020575) supported by Natural Science Foundation of Liaoning Province, China; Project(F16-205-1-14) supported by Science and Technology Program of Shenyang City, China

Received date: 2015-09-19; Accepted date: 2016-03-22

Corresponding author: WANG Chun-gang, PhD, Professor; Tel: +86-24-25134766; E-mail: ralphsy@163.com