ESO-based robust predictive control of lunar module with fuel sloshing dynamics
来源期刊:中南大学学报(英文版)2017年第3期
论文作者:宋征宇 颜钢锋 赵党军
文章页码:589 - 598
Key words:extended state observer; predictive controller; parameter perturbation; fuel sloshing; lunar module
Abstract: An extended-state-observer (ESO) based predictive control scheme is proposed for the autopilot of lunar landing. The slosh fuel masses exert forces and torques on the rigid body of lunar module (LM), such disturbances will dramatically undermine the stability of autopilot system. The fuel sloshing dynamics and uncertainties due to the time-varying parameters are considered as a generalized disturbance which is estimated by an ESO from the measured attitude signals and the control input signals. Then a continuous-time predictive controller driven by the estimated states and disturbances is designed to obtain the virtual control input, which is allocated to the real control actuators according to a deadband logic. The 6-DOF simulation results reveal the effectiveness of the proposed method when dealing with the fuel sloshing dynamics and parameter perturbations.
Cite this article as: SONG Zheng-yu, YAN Gang-feng, ZHAO Dang-jun. ESO-based robust predictive control of lunar module with fuel sloshing dynamics [J]. Journal of Central South University, 2017, 24(3): 589-598. DOI: 10.1007/ s11771-017-3460-6.
J. Cent. South Univ. (2017) 24: 589-598
DOI: 10.1007/s11771-017-3460-6
SONG Zheng-yu(宋征宇)1, 2, YAN Gang-feng(颜钢锋)1, ZHAO Dang-jun(赵党军)3
1. College of Electrical Engineering, Zhejiang University, Hangzhou 310058, China;
2. Beijing Aerospace Automatic Control Institute (BAACI), Beijing 100854, China;
3. School of Aeronautics and Astronautics, Central South University, Changsha 410083, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: An extended-state-observer (ESO) based predictive control scheme is proposed for the autopilot of lunar landing. The slosh fuel masses exert forces and torques on the rigid body of lunar module (LM), such disturbances will dramatically undermine the stability of autopilot system. The fuel sloshing dynamics and uncertainties due to the time-varying parameters are considered as a generalized disturbance which is estimated by an ESO from the measured attitude signals and the control input signals. Then a continuous-time predictive controller driven by the estimated states and disturbances is designed to obtain the virtual control input, which is allocated to the real control actuators according to a deadband logic. The 6-DOF simulation results reveal the effectiveness of the proposed method when dealing with the fuel sloshing dynamics and parameter perturbations.
Key words: extended state observer; predictive controller; parameter perturbation; fuel sloshing; lunar module
1 Introduction
In recent decades, people dedicate extreme passions to the planetary explorations again: researches on a new generation of planetary landers to the lunar and other celestial bodies have been made by NASA [1] and the Chang’e Project has been implemented by China. However, the robotic planetary entry is still a challenging mission since the pin-point landing must be achieved by guidance and control system in the present of various disturbances in an unpredictable environment [2].
In general, due to no aerodynamic consideration, the lunar descent problem is relatively easy among more challenging entry problems. Actually, the Apollo lunar spacecraft has successfully landed on the moon in 1969. However, researchers are still pursuing some new control methods by applying recent developments in computer science and sensor techniques. An optimal feedback control strategy is employed in the guidance and control design for the lunar module soft landing in order to minimize the fuel consumption [3]. A back-stepping- based control method is used for the terminal phase of lunar landing [4]. Moreover, nonlinear neuro-control [5] and feedback linearization [6] are also used for the high performance control of lunar landers. However, these mentioned methods did not consider the fuel sloshing dynamics which practically exist in the spacecraft with fuel propellant and dramatically exert effects on the overall dynamics of the spacecraft.
A variety of passive techniques, such as baffles and bladders, can be used to alleviate the effects of fuel sloshing dynamics [7], however, these passive methods cannot completely eliminate sloshing effects, moreover, additional structural mass may raise the fuel consumption [8]. Several linearization-based methods [2, 8-10] have been proposed for accommodating the fuel slosh dynamics of space vehicles. In Ref. [8], the prominent propellant slosh dynamics such as the internal dynamics is approximated by the well-known mass- spring model, then a Lyapunov-based nonlinear feedback control law is proposed for the stabilization of upper-stage rocket. Note that the analogy fuel slosh model parameters are included in the controller, and to some degree, the slosh model errors will undermine the control performance. To overcome this shortage, a sliding mode disturbance observer (SMDO) is proposed to estimate the disturbance mainly including the fuel sloshing dynamics, and an SMDO-drived high order sliding mode control law is designed for the pitch control of the lunar module (LM) of Apollo 10, therefore efficiently suppressing the effects of slosh dynamics [2].However, the potential robustness cannot be guaranteed due to the essence of the linearization technique.
This work mainly focuses on the attitude stabilization for the descent of LM with fuel slosh dynamics. The rigid motion equations of LM and the coupled fuel sloshing dynamics are modeled first. Since the guidance design is not the emphasis in this work, a simple optimal guidance strategy from Ref. [11] is employed to provide the commanded acceleration vector, from which the commanded thrust magnitude and the commanded attitude can be extracted quickly. To facilitate the attitude controller design, we introduce the generalized disturbances which include various disturbances induced by fuel slosh dynamics, parameters perturbations and other model errors. After pure algebraic transformations on the attitude error dynamics, we have three independent second order single-in-single- out (SISO) systems. Motivated by Ref. [12], for such SISO systems we propose an NLESO-based predictive control strategy, in which, the NLESO is used for the reconstruction of the error states and the generalized disturbances from the input signals and the measured attitude signals provided by the inertial navigation system; and the robust predictive control law based on the observations of NLESO aims to minimize the prescribed control performance index. Numerical simulations reveal the robustness of the proposed method while dealing with slosh dynamics and parameter perturbations in the scenario of LM’s landing phase.
2 Problem formulations
To describe the motion of LM, we define some right-handed reference frames, as illustrated by Fig. 1. The moon centered inertia (MCI) frame with origin M located on the center of the moon is further defined with the positive zI axis pointing to the arctic pole and xI axis locating in the moon’s equatorial plane and pointing to the zero-degree-longitude line at the zero time instant. Further, we define another inertia frame P whose origin is identical to the origin of MCI frame and xp axis points to the prescribed landing site while zp locates in the motion plane of LM and points to the motion direction. The landing site is given by the longitude α0 and latitude β0. The vehicle structural frame S and the body frame B are defined with the same axis directions, +x axis is along the nominal thrust direction, and +z axis is along the positive motion direction, while +y axis completes the right handed frame. The origin of B frame locates on the mass center of LM, while S frame’s origin locates on the center of the bottom of the LM.
Using the rotation matrices from the Euler (2, 3, 1) rotations, the transformation matrix from B frame to P frame can be expressed as
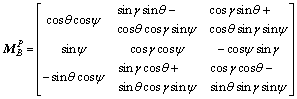 (1)
(1)
where γ, θ and ψ represent roll, pitch and yaw angles, respectively. In the remainder of this work, the superscript notation will represent the expression of a quantity in a particular frame, for an example, f B denotes a force vector in body frame B.
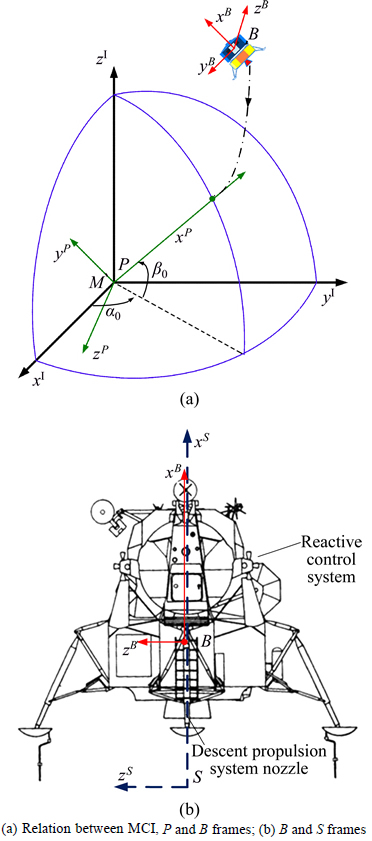
Fig. 1 Reference frames definition:
The approach phase of LM descending is considered in this work, thus it is reasonable to ignore the moon’s rotation and assume a spherical gravitational field in order to simplify the problem. The fuel slosh dynamics of four propellant tanks (including two fuel (Aerozine-50) tanks and two oxidizer (N2O4) tanks) of the descent propulsion system (DPS) are considered, meanwhile, since propellant mass of the reactive control system (RCS) is so small that its sloshing effects on LM are ignored. Unlike the quaternion-based motion model in Ref. [13], we present the rigid motion equations of LM based on the Euler angles as follows.
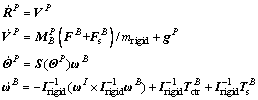 (2)
(2)
where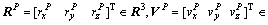
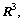 and
and 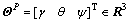 , respectively, are the position, velocity and attitude vectors of LM, and
, respectively, are the position, velocity and attitude vectors of LM, and
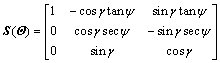 (3)
(3)
The gravitational acceleration is given by  with the moon’s gravitational
with the moon’s gravitational
parameter 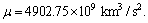 The total LM mass and inertial tensor are divided into the rigid parts and the sloshing parts, i.e.,
The total LM mass and inertial tensor are divided into the rigid parts and the sloshing parts, i.e., and
and  FB and
FB and 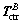 respectively are the total thrust vector and the control torque vector provided by the DPS and RCS. Actually, the DPS provides main thrust force and limit control torque during descending, while the RCS mainly provides attitude control authority and its force acted on the LM is far smaller than that of DPS. Two electrically servo-actuated gimbal drive actuators make the DPS nozzle deviates from its nominal position at a maximum rate of 0.2 (°)/s, meanwhile the maximum deviation angle is limited within ±6°. The main thrust line slightly deviates from the vehicle mass center thereby a limited control torque for attitude. The thrust vector of DPS in body frame is given by
respectively are the total thrust vector and the control torque vector provided by the DPS and RCS. Actually, the DPS provides main thrust force and limit control torque during descending, while the RCS mainly provides attitude control authority and its force acted on the LM is far smaller than that of DPS. Two electrically servo-actuated gimbal drive actuators make the DPS nozzle deviates from its nominal position at a maximum rate of 0.2 (°)/s, meanwhile the maximum deviation angle is limited within ±6°. The main thrust line slightly deviates from the vehicle mass center thereby a limited control torque for attitude. The thrust vector of DPS in body frame is given by
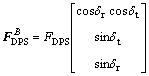 (4)
(4)
where △r and △t are the gimbal angles of the nozzle, FDPS is the thrust magnitude of DPS. Correspondingly, the limited control torque is
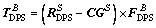 (5)
(5)
where 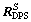 and CGS respectively are the location of the DPS nozzle center and the location of the vehicle mass center in S frame.
and CGS respectively are the location of the DPS nozzle center and the location of the vehicle mass center in S frame.
The RCS consists of sixteen reaction control jets which are divided into four clusters. In each cluster, one pair of jets is oriented along the xB axis, and the other pair locates in the plane of rotation about the xB axis. Each firing reaction control jet produces the constant thrust force fi=fjet=445 N along its thrust direction ui in B frame, therefore the total force provided by the RCS is
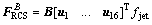 (6)
(6)
where 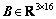 is the jet selection matrix, which is determined by the desired control torques of RCS. Further, the control torque provided by a firing jet is decided by
is the jet selection matrix, which is determined by the desired control torques of RCS. Further, the control torque provided by a firing jet is decided by
 (7)
(7)
where  is the location of the ith jet in the S frame, then the total control torque provided by RCS is given as
is the location of the ith jet in the S frame, then the total control torque provided by RCS is given as
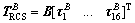 (8)
(8)
Thus the control force and torque are given as
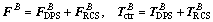 (9)
(9)
where  and
and 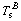 are the forces and torques exerted by the slosh mass which refers to the sloshing mass of propellant tanks including two fuel tanks and two oxidizer tanks.
are the forces and torques exerted by the slosh mass which refers to the sloshing mass of propellant tanks including two fuel tanks and two oxidizer tanks.
In general, the slosh dynamic of each cylindrical tank of LM is modeled as a spring and damper system (the details can be found in the Appendix A [13]) as follows
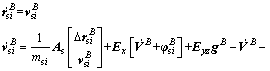
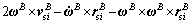 (10)
(10)
where  and
and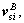 respectively are the position and velocity vector of the sloshing mass in the ith tank,
respectively are the position and velocity vector of the sloshing mass in the ith tank, 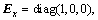
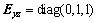 ,
,
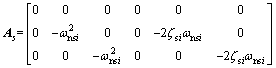
and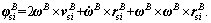 Further, ζsi and ωnsi are the equivalent second-order damping ratio and natural frequency for the slosh mass system of the ith tank, △ denotes the displacement of the slosh mass center from its nominal reference position. Note that the damping ratio and natural frequency are determined by the dimensions of the tank, the total liquid mass and the liquid density, consequently, they are changing during the flight due to the decreasing propellant mass.
Further, ζsi and ωnsi are the equivalent second-order damping ratio and natural frequency for the slosh mass system of the ith tank, △ denotes the displacement of the slosh mass center from its nominal reference position. Note that the damping ratio and natural frequency are determined by the dimensions of the tank, the total liquid mass and the liquid density, consequently, they are changing during the flight due to the decreasing propellant mass.
The sloshing forces resulted from sloshing propellant are opposite of the forces exerted on the slosh mass, meanwhile, the axial acceleration of the slosh mass with respect to the vehicle should be considered. It is reasonable to assume that the major component of the acceleration is along the xB axis of B frame. Hence, the slosh force and torque resulted from the ith propellant tank are formulated as
 (11)
(11)
and further we have 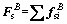 and
and 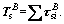
According to Eqs. (2), (10) and (11), the motion dynamics of LM and the slosh dynamics tightly couple with each other in acceleration, thus the model should be simultaneously solved. In fact, the simultaneous solution can be reasonably approximated by successively computing the required accelerations in the adjacent integration time steps, which are sufficiently small with respect to the closed-loop system.
3 Autopilot system design
In light of the mathematical model of LM, the attitude control authority is provided by both the continuous gimbal drive actuator, i.e., DPS, and the expensive but effective firing jets of RCS. Then for such a over-actuated system, the autopilot system design contains two phases: 1) design the total virtual commanded control input; and 2) allocate the virtual input to each actuators according to some certain logic. To facilitate the autopilot design, we present an ESO-based predictive control method first.
3.1 ESO-based predictive control
Consider a second order SISO nonlinear system as follows:
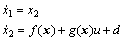 (12)
(12)
where 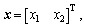 u is the input, y is the system output, and d is the unknown bounded and differentiable disturbances, meanwhile f and g are bounded smooth functions of their arguments. Further we define that
u is the input, y is the system output, and d is the unknown bounded and differentiable disturbances, meanwhile f and g are bounded smooth functions of their arguments. Further we define that 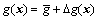 with a constant part
with a constant part 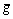 and a bounded smooth part △g(x). The goal of this work is to design an output-feedback controller for system (12) in order to perfectly track the reference output yr, which is assumed to be smooth enough such that its finite derivatives are bounded.
and a bounded smooth part △g(x). The goal of this work is to design an output-feedback controller for system (12) in order to perfectly track the reference output yr, which is assumed to be smooth enough such that its finite derivatives are bounded.
Denoting the tracking error by e=y-yr yields e=e1=x1-yr and e2=x2-yr, we henceforth have the tracking error dynamics as follows
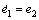
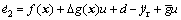

 (13)
(13)
According to Refs. [14, 15], there has a reasonable assumption the time mapping function 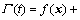
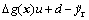 is bounded and differentiable, and the function Γ(t) can be called the generalized disturbance. Thus the tracking problem (12) is converted into a regulation problem (13).
is bounded and differentiable, and the function Γ(t) can be called the generalized disturbance. Thus the tracking problem (12) is converted into a regulation problem (13).
In most cases, the differential signal  cannot be directively obtained, meanwhile, the generalized disturbance Γ(t) has no explicit form. Thus, in order to estimate the error state e2 and the generalized disturbance Γ(t) from the measured output y and the reference trajectory yr, a nonlinear extended state observer is designed as follows [16, 17]
cannot be directively obtained, meanwhile, the generalized disturbance Γ(t) has no explicit form. Thus, in order to estimate the error state e2 and the generalized disturbance Γ(t) from the measured output y and the reference trajectory yr, a nonlinear extended state observer is designed as follows [16, 17]
 (14)
(14)
where  and ε are the design parameters. In light of theorem 2.2 in Ref. [16], given appropriate observer parameters, the observer states converge into the region defined by
and ε are the design parameters. In light of theorem 2.2 in Ref. [16], given appropriate observer parameters, the observer states converge into the region defined by 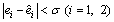 and
and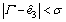 , where σ is a sufficiently small positive number, in a finite time Tε depends on the choice of ε.
, where σ is a sufficiently small positive number, in a finite time Tε depends on the choice of ε.
Given the present control u(t) at time instant t, the response of the error system at time instant t+△ can be predicted by the current error states in light of Taylor series, thus,
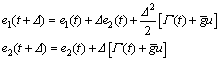 (15)
(15)
The predictive control performance index is given as
 (16)
(16)
where and R≥0, respectively, are the weightings on the predicted tracking errors
and R≥0, respectively, are the weightings on the predicted tracking errors 
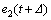 and the present control input u(t). Irrespective of the control saturations, applying
and the present control input u(t). Irrespective of the control saturations, applying 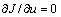 to Eq. (16) yields the commanded control input as follows
to Eq. (16) yields the commanded control input as follows
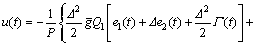
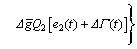 (17)
(17)
where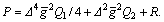 Note that the sufficiency condition of optimal control, i.e.,
Note that the sufficiency condition of optimal control, i.e.,  holds while
holds while  and R≥0. The performance of the predictive controller (17) is determined by the designed parameters △, Q1, Q2 and R. However, the required knowledge of the error state e2 and the generalized disturbance Γ(t) are not directively available. Fortunately, e2 and Γ(t) can be replaced by the observer signals
and R≥0. The performance of the predictive controller (17) is determined by the designed parameters △, Q1, Q2 and R. However, the required knowledge of the error state e2 and the generalized disturbance Γ(t) are not directively available. Fortunately, e2 and Γ(t) can be replaced by the observer signals 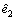 and
and 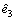 provided by the nonlinear ESO (14) thereby an ESO-based predictive controller as follows
provided by the nonlinear ESO (14) thereby an ESO-based predictive controller as follows
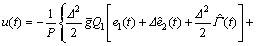
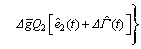 (18)
(18)
where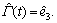 The closed-loop stability of the controller (18) is stated by the following theorem.
The closed-loop stability of the controller (18) is stated by the following theorem.
Theorem 1: For error system (13), given the designed parameters Q1, Q2≥0 and R≥0, the ESO-based predictive controller (18), in which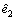 and
and are provided by the ESO (14) with appropriate parameters α and ε such that the finite-time convergence performance, guarantees the tracking errors ei (i=1, 2) are uniformly ultimately bounded.
are provided by the ESO (14) with appropriate parameters α and ε such that the finite-time convergence performance, guarantees the tracking errors ei (i=1, 2) are uniformly ultimately bounded.
Proof: Define the estimation errors 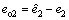 and
and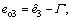 then there are
then there are 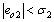 and
and 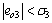 with σ2 and σ3 are positive small numbers. The controller (18) can be rewritten as
with σ2 and σ3 are positive small numbers. The controller (18) can be rewritten as


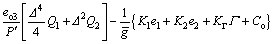 (19)
(19)
where 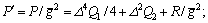 K1, K2 and KΓ are the functions of the design parameters, i.e., △, Qi and R, meanwhile, Co depends on the observer errors eo2 and eo3.
K1, K2 and KΓ are the functions of the design parameters, i.e., △, Qi and R, meanwhile, Co depends on the observer errors eo2 and eo3.
Substituting Eq. (19) into the error system (13) yields the closed-loop dynamics as follows
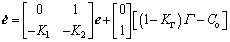

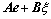 (20)
(20)
where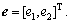 It is easy to verify that the eigenvalues of the system matrix A is negative hence the closed-loop Eq. (20) is bounded-input-bounded-output (BIBO) stable.
It is easy to verify that the eigenvalues of the system matrix A is negative hence the closed-loop Eq. (20) is bounded-input-bounded-output (BIBO) stable.
Further, we have
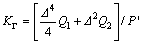
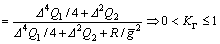 (21)
(21)
Reasonable choice of the parameters △, Q1, Q2 and R can make the value of 1-KΓ<<1. In light of the bounded assumption about the generalized disturbance Γ, we have |Γ|<=Γmax, thus (1-KΓ)|Γ|<<Γmax. Note that, if R=0, i.e., there is no penalty on control input, we have 1-KΓ=0, thus, the generalized disturbance Γ is completely canceled in the closed-loop Eq. (20).
For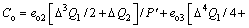
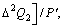 we have
we have
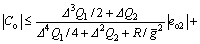
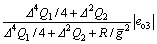
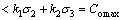 (22)
(22)
Consequently,
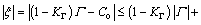
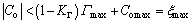 (23)
(23)
Solving Eq. (20) yields
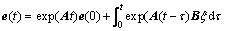 (24)
(24)
where e(0) is the initial error. According to the Cauchy Schwarz inequality, there has

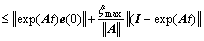 (25)
(25)
Since the matrix A is stable, then the following inequality holds:
 (26)
(26)
Hence, e(t) converges into the region defined by 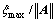 in an exponentially asymptotic manner, i.e., the tracking error e1 and e2 are uniformly ultimately bounded to the region with a small radius
in an exponentially asymptotic manner, i.e., the tracking error e1 and e2 are uniformly ultimately bounded to the region with a small radius 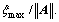 Note that the radius depends on the choice of the designed parameters △, Q1, Q2 and R, especially, when R=0, the generalized disturbance is compensated completely.
Note that the radius depends on the choice of the designed parameters △, Q1, Q2 and R, especially, when R=0, the generalized disturbance is compensated completely.
Remark 1: Note that, the controller (18) consists of the correction component resulted from the predictive error in the future time instant. Irrespective of the predictive corrections, the controller can be rewritten as a normal PD controller with the generalized compensation:
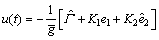 (27)
(27)
where K1>0 and K2>0. The controller (27) renders a closed-loop system as uniformly ultimately stability for system (12), this can be found in Ref. [14]. The comparison study between the controllers (18) and (27) will be conducted in the 4th section of this work. The results show that it is difficult to tune the parameters K1 and K2 in Eq. (27), meanwhile, the sloshing dynamics of the vehicle are hard to be suppressed by the controller Eq. (27).
3.2 Attitude tracking control
To facilitate the attitude controller design according to the method provided in the last subsection, the rotational motion equations in Eq. (2) is rewritten as follows
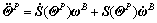
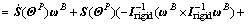
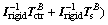 (28)
(28)
From Eq. (3) we have
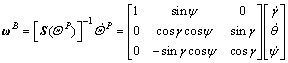 (29)
(29)
Then Eq. (28) becomes
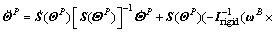
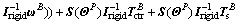

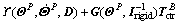 (30)
(30)
where 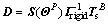 is the disturbance term resulted from the propellant sloshing,
is the disturbance term resulted from the propellant sloshing, 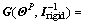
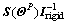 is the control effective matrix which is time varying. Note that the roll and yaw angles during the descent are small since the motion LM is often confined in the pitch plane, thus
is the control effective matrix which is time varying. Note that the roll and yaw angles during the descent are small since the motion LM is often confined in the pitch plane, thus 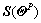 is almost a diagonal matrix according to Eq. (3). Further, the inertia matrix Irigid sourced from a lookup table is a diagonal dominance
is almost a diagonal matrix according to Eq. (3). Further, the inertia matrix Irigid sourced from a lookup table is a diagonal dominance
matrix. Thus, let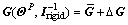 with that
with that 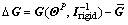 and
and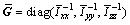 is a constant diagonal matrix, then Eq. (30) becomes
is a constant diagonal matrix, then Eq. (30) becomes
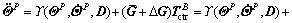
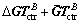 (31)
(31)
Defining the attitude tracking error 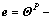
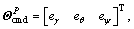 where
where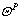 is real-timely provided by the navigation unit, yields the error dynamics
is real-timely provided by the navigation unit, yields the error dynamics
 (32)
(32)
Define a time mapping function Γ(t)= 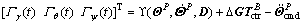 , consequently, the error system (32) can be written as follows.
, consequently, the error system (32) can be written as follows.
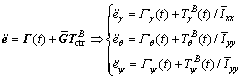 (33)
(33)
which is decoupled into three independent SISO systems like Eq. (13).
According to the ESO-based predictive control method proposed in the last subsection, we can design three nonlinear ESOs like Eq. (14) as follows
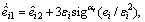
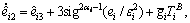
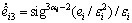 (34)
(34)
where 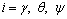 represents for three observers for roll, pitch and yaw channel, αi and εi are the designed observer parameters, and
represents for three observers for roll, pitch and yaw channel, αi and εi are the designed observer parameters, and 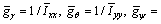
 In light of Eq. (18), the attitude tracking controllers for roll, pitch, and yaw are given as
In light of Eq. (18), the attitude tracking controllers for roll, pitch, and yaw are given as
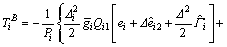
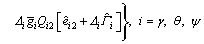 (35)
(35)
where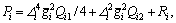 and △i, Qi1, Qi2 and Ri are the parameters to be tuned for the better control performance.
and △i, Qi1, Qi2 and Ri are the parameters to be tuned for the better control performance.
3.3 Autopilot architecture
Since the symmetrical structure of LM, the autopilot architectures for the pitch and yaw channel are identical, and have identical parameters. Figure 2 shows the autopilot diagram for the pitch channel, and the diagram for yaw channel is similar to Fig. 2.
The guidance module of the vehicle calculates the commanded attitude  according to the prescribed landing site and the current position and velocity provided by the navigation unit. A simple optimal feedback guidance law provided by Ref. [11] is used in this work to obtain the commanded attitude.
according to the prescribed landing site and the current position and velocity provided by the navigation unit. A simple optimal feedback guidance law provided by Ref. [11] is used in this work to obtain the commanded attitude.
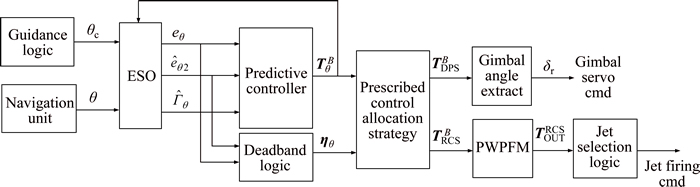
Fig. 2 Autopilot structure for pitch control
Fed by the attitude command θc and the measured attitude θ and the commanded torque 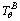 at the last time instant, the nonlinear ESO starts and provided the estimate signals
at the last time instant, the nonlinear ESO starts and provided the estimate signals 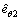 and
and 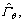 which are used to calculate the commanded torque
which are used to calculate the commanded torque 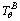 at the current time instant. The prescribed control allocation strategy is to reasonably allocate the commanded torque to different actuators, i.e., DPS and RCS. Note RCS propellant is very precious, hence the allocation strategy should minimize the usage of RCS. Similar to the allocation strategy proposed by Refs. [2, 13], a deadband logic is used to allocate the commanded torque to RCS and DPS. The RCS actuation is inhibited while the attitude error and the attitude error rates are within the deadband thresholds, i.e,
at the current time instant. The prescribed control allocation strategy is to reasonably allocate the commanded torque to different actuators, i.e., DPS and RCS. Note RCS propellant is very precious, hence the allocation strategy should minimize the usage of RCS. Similar to the allocation strategy proposed by Refs. [2, 13], a deadband logic is used to allocate the commanded torque to RCS and DPS. The RCS actuation is inhibited while the attitude error and the attitude error rates are within the deadband thresholds, i.e,
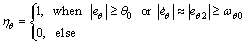 (36)
(36)
The deadband threshold for yaw control can be set in a similar way. Since DPS cannot provide the roll control authority, hence the commanded roll control torque is completely fulfilled by RCS.
According to Eqs. (4) and (5), we can extract the commanded gimbal angle △r and △t. Note that the mass center of vehicle is time-varying, and this will make the control logic more complicated. In practice, we can use an average mass center to replace the time-varying mass center, rendering a constant moment arm as follows.
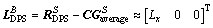 (37)
(37)
Considering the magnitude of gimbal angle is very small (less than 6°), then the thrust vector of DPS is approximated by
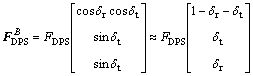 (38)
(38)
Then the control torque provided by DPS is
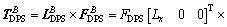
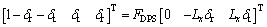 (39)
(39)
The gimbal angle commands can be extracted by
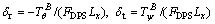 (40)
(40)
It should be noted that the thrust magnitude FDPS is not available during the flight. Practically, the thrust magnitude FDPS in Eq. (40) can be replaced by the commanded thrust magnitude provided by the guidance algorithm.
Since RCS thrusters exhibit discontinuous controls on the vehicle, the continuous commanded control torque should be modulated to activate the RCS jets. In this work, a technique of pulse width pulse frequency modulation (PWPFM) is employed to approximate the continuous torque calculated by the controller. The details of PWPFM can be found [18, 19].
4 Simulation
A full nonlinear 6-DOF simulation for the descent of Apollo LM 10 is developed by Simulink in order to evaluate the proposed ESO-based predictive controller. The liquid slosh dynamics for the four propellant tanks during descent stage and the actuator models of RCS and DPS is all considered in order to replicate the LM’s approach environment in detail. Further, the vehicle mass properties, including inertia tensor and mass center, are time-varying while the propellant is consumed. Since there are many parameters used in this work, it is hard to list all of them. Here the resources of the data are presented: the mass properties used are the nominal pre-PDI values for the “G” mission of the LM 10 [20]; the data of dimension and structure of LM, and they can be found in the appendix materials [10].
The designed parameters of the proposed autopilot system are listed in Table 1.
Table 1 Designed control parameters

The simulation trajectory starts from the position 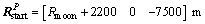 in P frame, i.e., the vehicle at an altitude of 2200 m and a downrange of 7500 m. The initial velocity is
in P frame, i.e., the vehicle at an altitude of 2200 m and a downrange of 7500 m. The initial velocity is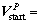
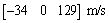 . The total approach phase of LM lasts about 150 s.
. The total approach phase of LM lasts about 150 s.
To show the advantages of the proposed method, a comparison study between the proposed method ESO-MPC and a PD controller with the generalized compensation like (27), namely ESO-PD, is conducted. The controller parameters K1 and K2 in Eq. (27) are both set as 4, which is tuned according to the method of Ref. [14] in order to obtain the similar tracking performance to the proposed method.
The simulation results are illustrated in Figs. 3-10. Figures 3 and 4 present the position and velocity of the vehicle during the descent under the effects of Eq. (35), and the results reveal that the trajectory of vehicle can well track the guidance command and accurately achieve to the prescribe landing site. Note that, in order to avoid the numerical unstability, the guidance algorithm is cut off 5 s in advance before landing. Figures 5 and 6 demonstrate the effects of fuel sloshing dynamics. It is obvious that the fuel sloshing frequency and magnitude are time-varying and depend on the consumptions of propellant. Note that in the final phase of Fig. 6, the magnitudes of sloshing force and torques become larger than before, the reason lies in the fact that the commanded acceleration and real-acceleration become larger since the smaller time-to-go used in the guidance algorithm to compute the commanded acceleration. As a comparison, the sloshing force and torques rendered by the ESO-PD controller (27) is shown in Fig. 7, which reveals that the simple improved PD controller cannot well suppress the sloshing dynamics, hence the attitude tracking performance is inferior than the ESO-MPC controller (35) (see Fig. 8).
The attitude tracking control performances of the proposed ESO-MPC controller and of the ESO-PD controller are presented in Fig. 8. It is clearly that the tracking errors of ESO-MPC method have excellent advantages over that of ESO-PD. The main reason is that
ESO-MPC well accommodates the sloshing dynamics since the introduction of predictive corrections. During the whole flight, except the initial attitude error, the maximum attitude error occurs in the final phase of the descent, and its magnitude does not exceed 2°.
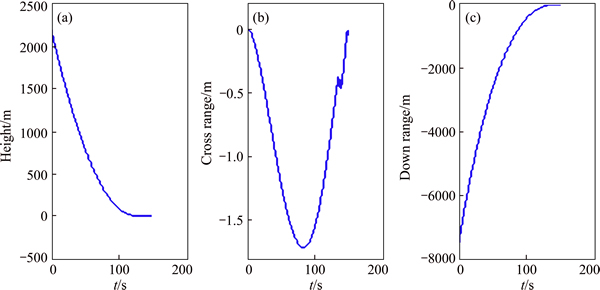
Fig. 3 LM position history in case of ESO-MPC
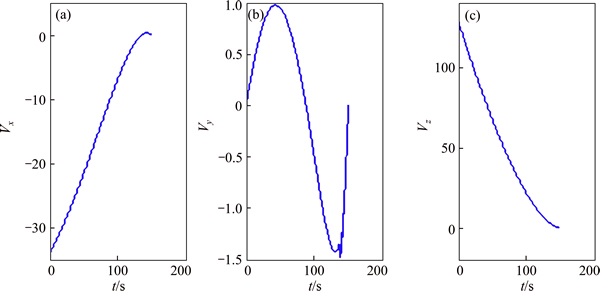
Fig. 4 LM velocity history in case of ESO-MPC
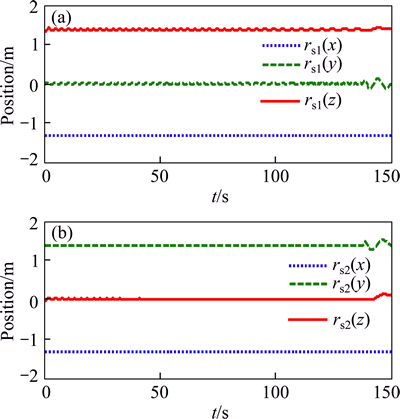
Fig. 5 Position history of sloshing mass centers in the case of ESO-MPC
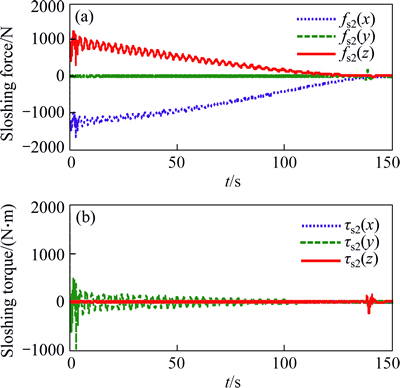
Fig. 6 Sloshing force and torques exerted on rigid body in the case of ESO-MPC

Fig. 7 Sloshing force and torques exerted on rigid body in the case of ESO-PD
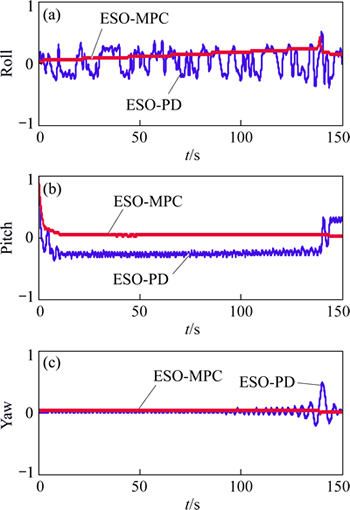
Fig. 8 Attitude tracking error history (ESO-PD: blue line; ESO-MPC: red line)
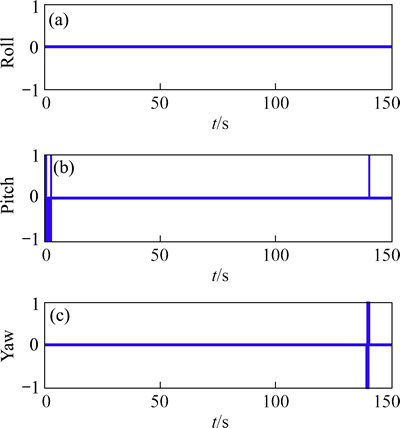
Fig. 9 RCS actuator commands
The corresponding control actuator commands of RCS and DPS are presented by Figs. 9 and 10. From Fig. 9, the deadband logic dramatically minimizes the usage of RCS, and the RCS jets fire only in a short period, meanwhile, the gimbal angles does not exceed its limit of 6° (shown in Fig. 10).
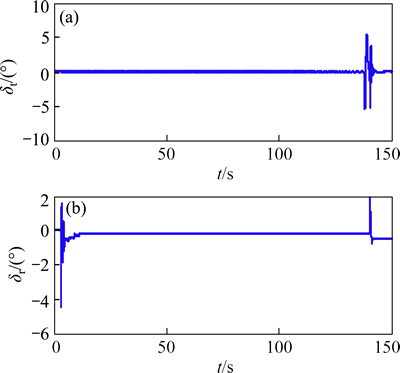
Fig. 10 DPS actuator commands
5 Conclusions
1) The proposed nonlinear ESO-based predictive control law utilizes the estimation of the error state and the generalized disturbance provided by ESO to overcome the difficulties resulted from the poor knowledge about the system to be controlled. Theoretical analysis reveals that the uniformly ultimately bounded stability is guaranteed by the proposed method.
2) Based on the proposed ESO-based predictive control method, an autopilot system for the descent of the lunar module LM10 of Apollo is developed. The propellant sloshing dynamics results in coupled disturbances, which are the main internal disturbance during the descent, meanwhile, the time-varying parameters are considered as parameter perturbations. The deadband logic is designed to allocate the commanded torque to RCS and DPS in order to minimize the usage of RCS propellant, and the technique of PWPFM is applied to activate the RCS jets. The simulation results reveal that the proposed method perfectly accommodates both disturbances and parameter perturbations. In the further research, the optimal control allocation should be considered in order to improve the control performance.
References
[1] COHEN B A. NASA’s robotic lunar lander development project [J]. Acta Astronautica, 2012, 79: 221-240.
[2] ORR J S, SHTESSEL Y B. Lunar spacecraft powered descent control using higher-order sliding mode techniques [J]. Journal of the Franklin Institute, 2012, 349 (1): 476-492.
[3] ZHOU Jing-yang, TEO K L, ZHOU Di. Nonlinear optimal feedback control for lunar module soft landing [J]. Journal of Global Opimization, 2012, 52(2): 211-227,
[4] ZHANG Fang, DUAN Guang-ren. Integrated translational and rotational control for the terminal landing phase of a lunar module [J]. Aerospace Science and Technology, 2013, 27(1): 112-126.
[5] WANG Da-yi, LI Tie-shou, YAN Hui. Nero-optimal guidance control for lunar soft landing [J]. Journal of Systems Engineering and Elecctronics, 1999, 10(3): 22-31.
[6] SIDI M J. Spacecraft dynamics and control: A practical engineering approach [M]. New York, US: Cambridge University Press, 1997.
[7] PETERSON L D, CRAWLEY E F, HANSMAN R J. Nonlinear fluid slosh coupled to the dynamics of a spacecraft [J]. AIAA Journal, 27(9): 1230-1240.
[8] RUBIO H J, REYHANOGLU M. Thrust-vector control of a three-axis stabilized upper-stage rocket with fuel slosh dynamics [J]. Acta Astronautica, 2014, 98: 120-127.
[9] LU P. Entry guidance: A unified method [J]. Journal of Guidance Control and Dynamics, 2014, 37 (3): 713-729.
[10] MORGAN D, CHUNG S J. Model predictive control of swarms of spacecraft using sequential convex programming [J]. Journal of Guidance Control and Dynamics, 2014, 37(6): 1725-1740.
[11] GUO Yan-ning, HAWKINS M. Waypoint optimized zero-effort- miss/zero-effort-velocity feedback guidance for mars landing [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 799-809.
[12] PANCHAL B, KOLHE J P, TALOLE S E. Robust predictive control of a class of nonlinear systems [J]. Journal of Guidance Control and Dynamics, 2014, 37(5): 1437-1445.
[13] ORR J S. Robust autopilot design for lunar spacecraft powered decent using high order sliding mode control [D]. Huntsville, US, the University of Alabama, 2009.
[14] ZHAO Dang-jun, WANG Yong-ji, LIU Lei. Robust fault-tolerant control of launch vehicle via gpi observer and integral sliding mode control [J]. Asian Journal of Control, 2013, 15(2): 614-623.
[15] ZHAO Dang-jun, JIANG Bing-yan. Adaptive fault tolerant control of heavy lifting launch vehicle via differential algebraic observer [J]. Journal of Central South University, 2013, 20(8): 2142-2150.
[16] GUO B Z, ZHAO Z L. On the convergence of an extended state observer for nonlinear systems with uncertainty [J]. Systems & Control Letters, 2011, 60(6): 420-430.
[17] ZHAO Dang-jun, YANG De-gui. Model-free control of quad-rotor vehicle via finite-time convergent extended state observer [J]. International Journal of Control, Automation, and Systems, 2016, 14(1): 242-254
[18] SARLI B V, SILVA A L, PAGLIONE P. Sliding mode attitude control using thrusters and pulse modulation for the ASTER mission [J]. Computational and Applied Mathematics, 2015, 34(2): 535-556.
[19] GENG Jie, SHENG Yong-zhi, LIU Xiang-dong. Finite-time sliding mode attitude control for a reentry vehicle with blended aerodynamic surfaces and a reaction control system [J]. Chinese Journal of Aeronautics, 2014, 27(4): 964-976.
[20] NASA. CSM/LM Spacecraft operational data book volume 3: Mass properties [M]. Texas, USA: NASA, 1969.
(Edited by FANG Jing-hua)
Cite this article as: SONG Zheng-yu, YAN Gang-feng, ZHAO Dang-jun. ESO-based robust predictive control of lunar module with fuel sloshing dynamics [J]. Journal of Central South University, 2017, 24(3): 589-598. DOI: 10.1007/ s11771-017-3460-6.
Foundation item: Project(020301) supported by the Manned Spaceflight Advanced Research, China; Project(14JJ3024) supported by Hunan Natural Science Foundation, China
Received date: 2015-11-09; Accepted date: 2016-12-01
Corresponding author: SONG Zheng-yu, Associate Chief Engineer, PhD; Tel: +86-13381130306; E-mail: zycalt12@sina.com

