J. Cent. South Univ. (2016) 23: 1176-1182
DOI: 10.1007/s11771-016-0367-6

Combining supervised classifiers with unlabeled data
LIU Xue-yan(刘雪艳), ZHANG Xue-ying(张雪英), LI Feng-lian(李凤莲), HUANG Li-xia(黄丽霞)
College of Information Engineering, Taiyuan University of Technology, Taiyuan 030024, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: Ensemble learning is a wildly concerned issue. Traditional ensemble techniques are always adopted to seek better results with labeled data and base classifiers. They fail to address the ensemble task where only unlabeled data are available. A label propagation based ensemble (LPBE) approach is proposed to further combine base classification results with unlabeled data. First, a graph is constructed by taking unlabeled data as vertexes, and the weights in the graph are calculated by correntropy function. Average prediction results are gained from base classifiers, and then propagated under a regularization framework and adaptively enhanced over the graph. The proposed approach is further enriched when small labeled data are available. The proposed algorithms are evaluated on several UCI benchmark data sets. Results of simulations show that the proposed algorithms achieve satisfactory performance compared with existing ensemble methods.
Key words: correntropy; unlabeled data; regularization framework; ensemble learning
1 Introduction
Pattern classification, as a significant branch of data mining, has been widely studied over the past years. Numerous theories and models, e.g., support vector machine [1], decision trees [2-3], and neural networks [3], have been proposed to address specified practical tasks. However, single model always cannot meet the demand of real applications. Consequently, studying effective ensemble technique has drawn intensively researching interests for researchers and practitioners.
In the last four decades, many ensemble techniques have been invented and successfully applied to the pattern classification learning. Ensemble learning is a technique that combines a set of alternative classifiers with certain fusion strategy. It has more flexibility in terms of representing labeled data than a single classifier. Empirically, classifier ensemble tends to have better results than single classifier due to its good generalization capability and favorable classification achievements.
The idea of performance improvement in classifier ensemble system has been proven to be true only when the combined base classifiers are accurate and diverse enough, which requires an adequate tradeoff between these two conflicting conditions [4]. In this perspective, the research of ensemble learning mainly falls into two categories. One focuses on generating a set of diverse base classifiers, and the other lays emphasis on combining the classifiers with effective fusion strategies. Amongst all ensemble algorithms, boosting [5-6] and bagging [7] are two classic approaches that focus on learning diverse base classifiers in the training process. Boosting generates a set of classifiers by using different labeled data sets which were determined by the performance of the former classifiers. Bagging algorithm generates several different labeled data sets by bootstrap sampling from the original labeled data set, and trains a set of classifiers from those labeled data sets. In terms of fusion strategy, it refers to combining the outputs of the base classifiers effectively. Simple fusion strategies, such as majority voting, maximum, minimum, average, and order weighted average, can be found in Refs. [8-11].
The aforementioned ensemble methods only take the advantage of the information of the labeled data. They fail to consider the internal relationship among unlabeled data. Actually, relationships among unlabeled data provide useful constraints on the classification task. In this work, we explore how to ensemble supervised classifiers by utilizing unlabeled data efficiently. A novel label propagation based ensemble (LPBE) approach is proposed to fuse the results of base classifiers. The proposed LPBE approach employs the correntropy first to construct a similarity graph among unlabeled data. The average classification results obtained from the base classifiers are then propagated on the constructed similarity graph under the regularization framework. By iterating, the classification accuracy is further enhanced.
The main contributions of this work are summarized as follows: first, a new label propagation based ensemble (LPBE) approach is presented. Unlike traditional ensemble algorithm, the proposed method combines the outputs of the base classifiers via unlabeled data graph. Second, the internal relationships between unlabeled data are considered creatively in the proposed ensemble approach. Third, the well-known regularization framework in semi-supervised learning is employed here to fuse the classifier results. The last one is that a semi-supervised LPBE method is also presented with the consideration of small labeled data being available.
2 Related works
The output of single supervised classifier is usually imprecise and uncertain. By combining the outputs of multiple base classifiers, we are aiming at a more accuracy classification decision. Conventional ensemble approaches, theories, and operators include bayesian method [12], decision template [13-14], Dempster- Shafer evidence theory (D-S) [15-16], fuzzy integrals [17], etc.
In the last decades, numerous new classifier ensemble algorithms are proposed. LIU [18] investigated and combined classifiers with different structures by utilizing a wide variety of fusion strategy, such as linear discriminants, sum-rule, product-rule, and weighted combination. ZHANG and ZHOU [19] analyzed sparse classifier ensembles with a weighted combination framework and proposed several linear programming techniques to combine base classifiers sparsely. The sparsity learning in Ref. [19] sought a sparse weight vector, whose value was either zero or nonzero, to fuse the outputs of base classifiers. The authors in Ref. [20] proposed a convex mathematical framework of classifier ensemble which considered both sparsity and diversity, while most existing methods just focused on either sparsity or diversity. In Ref. [21], the outputs of HMM classifiers were first combined with the D-S theory, and then a set of acceptance/rejection decision strategies were employed to improve the reliability of the combination. It was demonstrated in Ref. [22] that, by solving an optimization problem of upper integral, the proportion of each data was determined and assigned to different classifier combinations first. Then new unlabeled data were classified according to the properties. Finally, the optimal combination was selected according to its performance on these new unlabeled data.
In addition, KANG et al invented an optimization method with single classifier [23]. In their algorithm, a pixelwise SVM classifier was first adopted to generate the classification probability maps, and then the probability maps were optimized with the extended random walkers algorithm in a weighted graph. In Ref. [24], the authors proposed an ensemble method to address imbalanced data task. They first split the imbalances data into multiple balanced subsets, then trained a set of classifiers, and combined the outputs of these classifiers by specific rule last.
Ensemble methods in literature usually try to address the ensemble problem by the labeled data and the base classifiers. They fail to take the relation between unlabeled data into consideration. Consequently, in this work a label propagation based ensemble approach is proposed to combine the outputs of the base classifiers with the unlabeled data.
3 Methodology
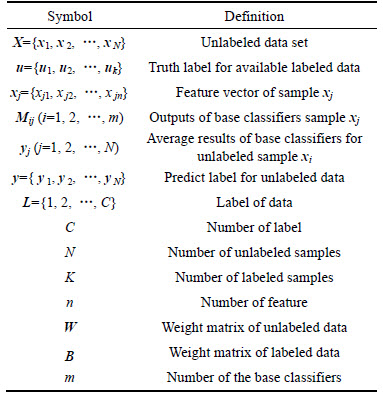
The main notations of this paper are illustrated in Table 1.
Table 1 Main notation used in this work
3.1 Correntropy
Most similarity matrixes in literature are based on distance, such as Euclidean distance, Mahalanobis distance and Minkowsk distance. In this work, a generalized correlation method-correntropy is utilized to implement similarity measure. The concept of correntropy is proposed in information theoretic learning (ITL) to process non-Gaussian signals [25]. It is a local similarity measure which contains information on both statistic distribution and temporal structure of the underlying dataset [26]. Assuming two arbitrary random variables x1 and x2, the correntropy function is defined by
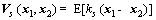 (1)
(1)
where kσ(·) is a symmetric definite kernel function that satisfies Mercer theory [27] and E[·] is the expectation operator. In practice, correntropy can be mathematically estimated by
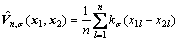 (2)
(2)
Gaussian kernel function is used in our method to map the input space to a higher dimensional feature space nonlinearly. The function of Gaussian kernel is given by
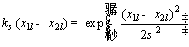 (3)
(3)
where σ refers as the kernel size parameter. In practice, the value of σ is crucial to the property of correntropy. So, in this work we determine the kernel size by SILVERMAN’s rule [28] of density estimation which provides a reasonable value.
 (4)
(4)
where A is a small value between the standard deviation of data and the data interquartile range scaled by 1.3; 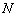 is the number of the samples.
is the number of the samples.
3.2 Learning with unlabeled data
The basic idea of the proposed label propagation based ensemble (LPBE) approach is taking full advantage of the information of unlabeled data. By constructing an unlabeled data based similarity graph and propagating preliminary results on the graph, the classification results are combined and further improved. Figure 1 shows the diagram of the general procedure of the proposed LPBE approach.
In Fig. 1, unlabeled data are used in two aspects: as an input of the well-trained base classifiers to generate base classification results, and as vertex of the constructed similarity graph. In LPBE approach, the average rule is employed to combine the outputs of the base classifiers. For unlabeled sample xj, the mathematical expression of the average rule is shown as
 (5)
(5)
The inspiration of the proposed LPBE approach is from graph-based semi-supervised method. In semi- supervised method, the vertexes of the graph contain both labeled data and unlabeled data, while in our method the vertexes of the graph are unlabeled data only. Like the graph-based semi-supervised method, the label propagation based ensemble approach consists of two parts: graph construction and label propagation.
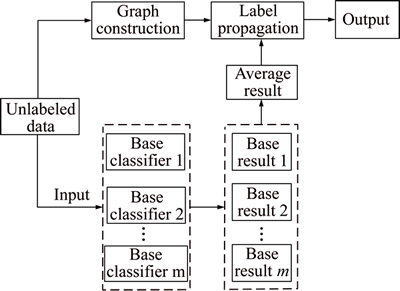
Fig. 1 Diagram of proposed LPBE approach
Construct a graph G=(V, E), where vertex set V is composed of all unlabeled data and E is the edge set with edge weight. Edge weight is the key issue in graph-based method and it is also a good way to reveal the relationship between vertexes. In LPBE approach the edge weight W is computed by correntropy which has been introduced above.
The label propagation process can be summarized as an estimation of the function f(·) on the graph, and it can be expressed in a regularization framework which is composed of a loss function and a regularizer [29]. The general expression of regularization framework can be shown as
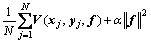 (6)
(6)
where the first term is an arbitrary loss function and the second term is a regularization term;  is the balance parameter. And as required in semi-supervised learning, in our method the function f(·) should satisfy the following conditions: 1) it should be close to the preliminary classification results, and 2) it should be smooth on the graph. Therefore, we formulate the label propagation problem as
is the balance parameter. And as required in semi-supervised learning, in our method the function f(·) should satisfy the following conditions: 1) it should be close to the preliminary classification results, and 2) it should be smooth on the graph. Therefore, we formulate the label propagation problem as
 s.t. f ≥0, f·1=1 (7)
s.t. f ≥0, f·1=1 (7)
where the first term is loss function, and it ensures that if the average result of sample xi is yi, the estimated final result fi should not deviate much to its initial result yi. The second term is a regularizer which imposes a constraint that the label can propagate smoothly over the graph. Wij represents the relationship between unlabeled data xi and xj which can be calculated by Eq. (2).
The problem of Eq. (7) is a convex quadratic programming problem which can be solved by label propagation algorithm [30]. By iterating Eq. (8), we can obtain the prediction probability for each unlabeled data.
 (8)
(8)
Especially, when α=0, the optimal f is equal to y. The final result can be obtained by Eq. (9).
 (9)
(9)
Details of graph construction and label propagation are summarized as follows:
1) Initialize parameters.
2) Calculate the average results of the base classifiers by Eq. (5).
3) Construct graph. Calculate the weight of the graph, if i≠j, Wij is calculated by Eq. (2), and if i=j, Wij=1.
4) Initialize label probability. The initial label probability is f(0)=y.
5) Propagate labels. Iterate Eq. (8) until it convergences.
6) Annotate labels. Label each sample by Eq. (9).
3.3 Incorporating labeled data
In previous section, we assume that we have no access to the labeled data. The fusion task is completed by just taking advantage of unlabeled data. In this section, we assume that K labeled data which contain feature and their corresponding ground truth labels u are available. The fusion task is further addressed by incorporating with these labeled data. This is actually a semi- supervised learning problem, so we call the method as semi-LPBE algorithm.
Another graph is constructed where the vertexes of the graph are both unlabeled data and labeled data. Similar to the weight matrix W between unlabeled data, another weight matrix B is also defined. Weight matrix B demonstrates the relationship between labeled data and unlabeled data, which also can be calculated by correntropy.
Label propagation process also obeys the regularization framework rules. As Eq.(6) can be extended to Eq. (10) in Ref. [29].
 (10)
(10)
Equation (7) can also be extended as follows:

 s.t. f≥0, f·1=1 (11)
s.t. f≥0, f·1=1 (11)
where  is also a balance parameter. Equation (11) also can be solved by label propagation algorithm.
is also a balance parameter. Equation (11) also can be solved by label propagation algorithm.
 (12)
(12)
In this process, preliminary results adaptively propagate over the bi-graph. The final classification results are constrained by both labeled data and unlabeled data.
4 Experiments and analysis
4.1 Database and experimental setting
The proposed methods were evaluated on 15 benchmark datasets from UCI machine repository. Details of the introduction of these datasets can be found in Ref. [31]. Table 2 summarizes the 15 UCI data sets used in this work.
Table 2 Descriptions of data sets

In order to verify the effectiveness of the proposed ensemble approach, BP network model, KNN model and multi-layer perceptron neural networks (MLP) are employed as base classifiers. The models for comparison include three base classifiers, average rule, product rule, Bayes model, decision template (DT) and Dempster- Shafer evidence model (D-S). The details of these comparison methods can be found in Ref. [32].
The result is measured by the classification accuracy, i.e., the percentage of the number of correct classified documents in the entire dataset. Each learning problem is carried out with 5-fold cross validation test, and repeated three times. The final result is the average result of each learning problem. It is worth to mention that in semi- LPBE algorithm, small labeled data are incorporated to further improve the performance. In semi-LPBE experiments, 10% of the labeled data is randomly taken to incorporate the label propagation process.
4.2 Experimental results
In order to vividly display the process of the LPBE method, an artificial dataset is generated. The artificial dataset is a two-dimensional dataset and has two classes. The LPBE approach is tested on the artificial data. Figure 2 presents the ideal classification results, average classification results of the base classifiers, and the LPBE classification results with different numbers of iterations respectively.
Figure 2(a) shows the ideal classification result, and Fig. 2(b) gives the average results of the base classifiers. Figures 2(c) and (d) show the results of LPBE algorithm with 15 iterations and 25 iterations, respectively. We can see from the marked part, compared with Fig. 2(b), Figs. (c), (d) correct some wrong labels. Especially, in Fig. 2(d) after 25 times iterates there is only one wrong label left.
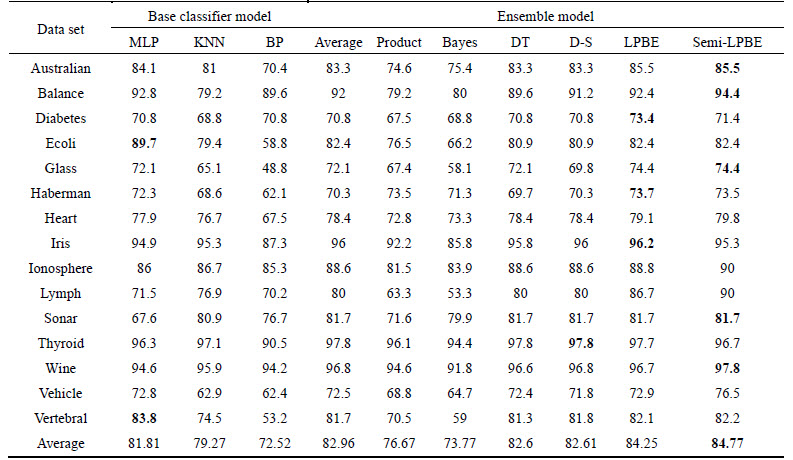
The proposed LPBE and semi-LPBE method were also evaluated on aforementioned UCI benchmark datasets. Table 3 summarizes the classification results of base classifier models and different ensemble methods with the best classification accuracy bold. The average accuracy of each model is shown in the last row of the table.
We can find from Table 3, the proposed LPBE and semi-LPBE approach usually have better performance than the three base classifiers on the 15 UCI data sets. However, there are exceptions. Take the Ecoli data set for an example, the best classification result of base classifier is 89.7%, while the best result of the proposed approach is only 82.4%. The same situation happens on the Vertebral data set. Actually, this is easy to understand, the performance of the proposed ensemble approach relies on all the three outputs of the base classifiers. Although one of the base classifier (MLP) has high classification accuracies, the accuracies of BP networks are low, which makes a negative effect on the fusion process.
Compared with other ensemble models, the proposed LPBE and semi-LPBE also have relatively high classification accuracy. From this table, we can see that the average rule, DT model and D-S model have better performance than other classic models used in this work. LPBE achieves the average classification accuracy with 84.25%, which increased the average accuracy by 1.29% compared with average rule and by 1.65% and 1.64% compared with DT and D-S models, respectively. Moreover, semi-LPBE achieves higher average performance compared with LPBE by 0.52%.

Fig. 2 Ensemble process of LPBE approach on artificial dataset:
Table 3 Classification accuracy (%) of different models
4.3 Parameter sensitivity
The sensitivity of α is evaluated in LPBE algorithm by tuning it from 0.1 to 0.7 with 0.05 as interval. Five of the UCI datasets were selected for testing. Because of random partition of the data set, each learning task is conducted 15 times with the same value of α. The average classification results are shown in Fig. 3. As we can see from the figure, when 0.1≤α≤0.3, the LPBE has relative high classification accuracy. Therefore, we suggest the value of α in the proposed LPBE approach can be selected to be in the range from 0.1 to 0.3. In semi-LPBE algorithm, the value of parameter β can also be selected in the same range.

Fig. 3 Classification accuracy on UCI datasets with different α values
5 Conclusions
A label propagation based ensemble (LPBE) method has been proposed to most effectively combine the outputs of the base classifiers. In the proposed LPBE algorithm, an unlabeled data based graph is constructed first, where the weights of the graph were adopted to the correntropy function. Regularization framework was employed in the process of label propagation, and the classification results were further fused by iterating on the graph. Besides, a semi-LPBE algorithm was proposed by considering the situation when small labeled data were available. Simulations and comparison experiments on UCI datasets showed the superiority of the proposed method. The fusion accuracy may further be improved if the principle of K-nearest neighbor is employed in constructing the unlabeled data graph. The sensitivity of the parameter of the proposed model was also covered.
References
[1] ZHANG Jun, OU Jian-ping, ZHAN Rong-hui. Automatic target recognition of moving target based on empirical mode decomposition and genetic algorithm support vector machine [J]. Journal of Central South University, 2015, 22(4): 1389-1396.
[2] YUAN Yu-fei, SHAW M J. Induction of fuzzy decision trees [J]. Fuzzy Sets Syst, 1995, 69(2): 125-139.
[3] MITCHELL T M. Machine learning [M]. New York: McGraw-Hill Press, 1997.
[4] KUNCHEVA L I, WHITAKER C J. Measures of diversity in classifier ensembles [J]. Machine Learning, 2003, 51: 181-207.
[5] SCHAPIRE R. The strength of weak learn ability [J]. Machine Learning, 1990, 5(2): 197-227.
[6] YIN Xu-cheng, LIU Chang-ping, HAN Zhi. Feature combination using boosting [J]. Pattern Recognition Letters, 2005, 26(13): 2195-2205.
[7] BREIMAN L. Bagging predictors [J]. Machine Learning, 1996, 24(1): 123-140.
[8] BELLET A, HABRARD A, MORVANT E, SEBBAN M. Learning a priori constrained weighted majority votes [J]. Machine Learning, 2014, 97: 129-154.
[9] MORVANT E, HABRARD A, AYACHE S. Majority vote of diverse classifiers for late fusion [J]. Structural, Syntactic, and Statistical Pattern Recognition Lecture Notes in Computer Science, 2014, 8621: 153-162.
[10] HE Yu-lin, LIU J, HU Yan-xing, WANG Xi-zhao. OWA operator based link prediction ensemble for social network [J]. Expert Systems with Applications, 2015, 42(1): 21-50.
[11] LUDWIG O, NUNES U, RIBEIRO B, PREMEBIDA C. Improving the generalization capacity of cascade classifiers [J]. IEEE Transactions on Cybernetics, 2013, 43(6): 2135-2146.
[12] KUNCHEVA L I. Combining pattern classifiers: Methods and algorithms [M]. Hoboken: Wiley-Interscience Press, 2003.
[13] KUNCHEVA L I. Switching between selection and fusion in combining classifiers: An experiment [J]. IEEE Transaction on Cybernetics, 2002, 32(2): 146-156.
[14] MEHDI S H, ABEDIN V, HADI S Y. Extending Dempster-Shafer method by multilayer decision template in classifier fusion [J]. Expert System with Applications, 2011, 38(7): 8414-8418.
[15] SHAFER G. A Mathematical theory of evidence [M]. Princeton, NJ, USA: Princeton Univ Press, 1976.
[16] ZHANG Li-ye, PENG Zhong-ren, LI Li, WANG Hua. Road boundary estimation to improve vehicle detection and tracking in UAV video [J]. Journal of Central South University, 2014, 21(12): 4732-4741.
[17] DENG Xin-yang, ZHENG Xi, SU Xiao-yan, CHAN F, HU Yong, SADIQ R, DENG Yong. An evidential game theory framework in multi-criteria decision making process [J]. Applied Mathematics and Computation, 2014, 244: 783-793.
[18] LIU Cheng-lin. Classifier combination based on confidence transformation [J]. Pattern Recognition, 2005, 38(1): 11-28.
[19] ZHANG Li, ZHOU Wei-da. Sparse ensembles using weighted combination methods based on linear programming [J]. Pattern Recognition, 2011, 44(1): 97-106.
[20] YIN Xu-cheng, HUANG Kai-zhu, YANG Chun, HAO Hong-wei. Convex ensemble learning with sparsity and diversity [J]. Information Fusion, 2014, 20: 49-59.
[21] KESSENTINI Y, BURGER T, PAQUET T. A Dempster–Shafer theory based combination of handwriting recognition systems with multiple rejection strategies [J]. Pattern Recognition, 2015, 48: 534-544.
[22] WANG Xi-zhao, WANG Ran, FENG Hui-min, WANG Hua-chao. A new approach to classifier fusion based on upper integral [J]. IEEE Trans on Cybernetics, 2014, 44(5): 620-635.
[23] KANG Xu-dong, LI Shu-tao, FANG Le-yuan, LI Mei-xiu, BENEDIKTSSON J. Extended random walker-based classification of hyperspectral images [J]. IEEE Trans on Geoscience and Remote Sensing, 2015, 53(1): 144-153.
[24] SUN Zhong-bin, SONG Qin-bao, ZHU Xiao-yan, SUN He-li, XU Bao-wen, ZHOU Yu-ming. A novel ensemble method for classifying imbalanced data [J]. Pattern Recognition, 2015, 48(5): 1623-1637.
[25] LIU Wei-feng, POKHAREL P P, PRINCIPE J C. Correntropy: Properties and applications in non-gaussian signal processing [J]. IEEE Trans. Signal Processing, 2007, 55(11): 5286-5298.
[26] GARDE A. SORNMO L, JANE R, GIRALDO B F. Correntropy- based analysis of respiratory patterns in patients with chronic heart failure [C]// 31st Annual International Conference of the IEEE EMBS Minneapolis. Minnesota, USA, 2009.
[27] VLADIMIR V. The nature of statistical learning theory [M]. New York: Springer-Verlag Press, 1995.
[28] SANTAMARIA I, POKHAREL P P, PRINCIPE J C. Generalized correlation function: definition, properties, and application to blind equalization [J]. IEEE Transactions on Signal Processing, 2006, 54(6): 2187-2197.
[29] ZHU Xiao-jin. Semi-supervised learning literature survey [R]. Computer Sciences, University of Wisconsin-Madison, 2008.
[30] ZHOU Deng-yong, BOUSQUET O, LAL T N, WESTON J, SCHOLKOPF B. Learning with local and global consistency [J]. Advances in Neural Information Processing Systems, 2004, 16: 321-328.
[31] FRANK A, ASUNCION A. UCI machine learning repository [EB/OL] [2013-07-29]. http://archive.ics.uci.edu/html.
[32] POLIKAR R. Ensemble based systems in decision making [J]. IEEE Circuits and Systems Magazine, 2006, 6: 21-45.
(Edited by YANG Hua)
Foundation item: Project(20121101004) supported by the Major Science and Technology Program of Shanxi Province, China; Project(20130321004-01) supported by the Key Technologies R & D Program of Shanxi Province, China; Project(2013M530896) supported by the Postdoctoral Science Foundation of China; Project(2014021022-6) supported by the Shanxi Provincial Science Foundation for Youths, China; Project(80010302010053) supported by the Shanxi Characteristic Discipline Fund, China
Received date: 2015-05-27; Accepted date: 2015-11-10
Corresponding author: ZHANG Xue-ying, Professor, PhD; Tel: +86-13015475372; E-mail: zhangxy@tyut.edu.cn