文章编号：1004-0609(2009)06-1019-06

Ti-15-3合金热变形显微组织的分形

李  萍，薛克敏

 (合肥工业大学 材料科学与工程学院，合肥 230009)

摘  要：以Ti-15-3合金热压缩变形显微组织的TEM像作为研究对象，基于Matlab软件平台，开发了图像处理及分形分析程序，采用盒维数法对不同变形温度、变形程度和变形速率下的显微组织形貌进行了分形分析。结果表明：Ti-15-3合金热塑性变形显微组织具有分形特征，可以采用分形维数对其形貌进行定量描述，且显微组织的分形维数随着变形温度的升高而减小，随着变形程度和变形速率的增大而增大；随着流变应力的增大，与之相对应的显微组织的分形维数增大；分形维数反映了热变形过程中软化过程进行的程度和金属变形抗力的大小；分形维数越小，软化过程进行得越充分，金属的变形抗力越小。

关键词：Ti-15-3合金；热变形；显微组织；分形

中图分类号：TG146.2       文献标识码： A

Fractal on hot deformed microstructure of Ti-15-3 alloy

LI Ping, XUE Ke-min

(School of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract: On the basis of Matlab software, the image treatment and fractal analysis by box counting program were developed. The systematic fractal analysis of TEM images of Ti-15-3 alloy after compression deformation at different temperatures, strains and strain rates were conducted. The results show that the hot deformed microstructures of Ti-15-3 alloy have the characteristic of fractal and can be described quantitatively by fractal dimension. The fractal dimension decreases with increasing temperature and increases with increasing strain and strain rate. Furthermore, with increasing flow stress, the fractal dimension of corresponding microstructure increases. The fractal dimension reveals the degree of dynamic softening during hot deformation and the magnitude of deformation resistance. With decreasing fractal dimension, the softening degree increases and the deformation resistance decreases.

Key words: Ti-15-3 alloy; hot deformation; microstructure; fractal

分形理论是非线性科学的三大方向之一，是一种描述和处理具有自相似性非规则图形及客观对象有效的分析方法和建模工具，其根本特征在于实现了测度观的转变。因而，分形的出现为分析解决一些复杂、非线性系统问题提供了新的科学方法和认识方法，具有广阔和深远的实际应用前景^[1?2]。

显微组织是金属材料微观特征中最为本质的一个部分，其与工艺参数和材料性能之间关系的研究一直是材料科学与工程的核心内容。热塑性变形过程是十分复杂的高温、动态、瞬时过程，显微组织演变具有非线性和复杂性，很难用传统的数学工具或单一的显微组织特征参数去定量的描述^[3?4]。

大量研究表明^[5?8]，金属显微组织具有分形特征，且可以采用尺度不变的分形维数对其进行客观、全面地表征。一些研究工作者以金属显微组织中离散的点状、线状分布的典型夹杂物为研究对象，通过对不同等级夹杂物的分维测量，验证了夹杂物等级与分形维数之间的关系。有关晶粒尺寸与相应晶粒分形维数、珠光体的球化等级与分形维数间关系的研究工作也在进行中。另外，还有些工作者对变形铜和铜锰合金的TEM像进行了系统地分形研究，采用不同方法确定了其分形维数，对其一致性进行验证，并对分形位错结构的动力学机制进行了深入研究^[5?8]。

为此，本文作者基于分形理论和显微组织的透射电子显微分析(TEM)，对Ti-15-3合金热压缩变形显微组织进行了分形研究。从而为今后基于分形理论建立显微组织和工艺参数以及力学性能之间的定量关系奠定基础，具有重要的理论意义和应用价值。目前，关于钛合金热塑性变形显微组织的分形研究还鲜见   报道。

1  显微组织图像的二值化处理

采用计算机对热塑性变形显微组织进行分形研究，关键问题是显微组织图像中目标像素的提取。为此，首先要对显微组织的TEM像进行二值化处理。

灰度图像的二值化方法主要有全局阈值法和局部阈值法^[9]。在目标和背景的灰度差别较明显时，全局阈值法效果比较好且计算速度较快。而采用全局阈值法对图像进行二值化处理的关键是阈值的选取，其准确性直接影响对图像中特征信息进行描述分析的正确性。本研究采用模式识别中最大类间方差准则确定二值化的阈值。

设图像的灰度级为1~l，以灰度k将图像分为两个区域：灰度小于k的像素属于区域A；灰度大于k的像素属于区域B。则两个区域的方差为^[10]

在1~l间改变k值，使方差达到最大值时的k值即为最佳阈值，则二值化过程如下：

图1和2所示分别为变形温度为850 ℃、变形程度为0.6、变形速率为0.01/s的条件下，不同的放大倍数下Ti-15-3合金热变形显微组织的TEM像及其二值化图。

图1  不同放大倍数下Ti-15-3合金显微组织的TEM像

Fig.1  TEM images of Ti-15-3 alloy at different magnifications

图2  显微组织图像的二值化图

Fig.2  Binary images transformed from TEM images

2  显微组织分形维数的计算

分形维数是定量刻划分形体复杂结构的特征参数，表征了分形体的不规则程度。材料科学中常用的测定分形维数的方法有盒维数法、码尺法和小岛法。其中，盒维数法无论是对曲线还是对曲线围成的面都适用，与图像物理含义关系不大，因而广泛应用于二维图像分形维数的计算^[11?12]。

对于二维欧式空间的一系列点，用边长为d 的正方形盒子覆盖这些点，统计出至少包含一个点的方格数目N(d)，在双对数坐标系中用最小二乘法直线拟合数据点(?lnd, lnN(d))，若二者具有很好的线性关系，表明图像具有分形特性，且所得直线的斜率就是该图像分形维数的近似值。近似计算盒维数D_B为^[13]

在当前的分形研究中，正方形边长为d =2ⁿ(n≥0)，即正方形边长的最小尺寸为一个像素。

当图像边界处不能保证有完整的正方形盒子时，包含目标像素点的正方形盒子数目按下式计算^[14]：

式中  N₀(d)为包含目标像素的完整盒子的数目；A₀(d)为覆盖图像的完整盒子的面积；A为整个图像的面积。

本研究基于Matlab软件平台，自行开发了图像处理及分形分析程序，采用盒维数法计算了Ti-15-3合金热变形显微组织的分形维数。为验证程序的可靠性，分别计算了两种有规分形图形：直线(D_B=1)和正方形(D_B=2)的分形维数。其计算结果与理论值严格相等。

3  结果和分析

3.1  显微组织的分形特征

图3所示为变形温度为850 ℃、变形程度为0.6、变形速率为0.01/s的条件下Ti-15-3合金显微组织在不同的放大倍数下(见图1)的分形分析结果。由图3可以看出，放大不同倍数后，同一变形条件下的显微组织尽管形貌上完全不同，但位错等显微组织的分布具有相似规律，且数据点分布在线性相关性较好的直线附近。表明在当前变形条件下，在计算尺度范围内的不同尺度下，尽管Ti-15-3合金热塑性变形显微组织中位错线的长短、形状及分布并不相同，但从统计意义上来看，任何一部分和整体是相似的，其相应的测度不随尺度的改变而变化。即Ti-15-3合金热变形显微组织确实具有典型的分形特征，且可以采用分形维数这一特征参数来描述其组织形貌，综合反映位错线数量、分布、形状及显微组织的不规则程度。

图3  不同放大倍数下显微组织的分形维数

Fig.3  Fractal dimension of microstructure at different magnifications

材料不同、变形条件不同，位错排列方式也不同，形式的位错结构也不同，主要有均匀结构、周期或半周期有序结构以及自相似或分形结构^[15]。Ti-15-3合金是体心立方结构，合金在高温下的变形是一个热激活的过程，交滑移和攀移是其重要的形变机制。热塑性变形过程中，显微组织的演变不是瞬间完成的，而是要经过一个位错滑移、交滑移和攀移的过程。随着变形的进行，显微组织的演变是自相似的，因而最终形成的显微组织具有自相似性。且热塑性变形显微组织的演变反映到TEM像上，是一种不规则图像的变化。由此可见，热塑性变形显微组织具有分形的不规则性与自相似性特征。

3.2  变形条件对显微组织分形维数的影响

当其它变形条件相同时，变形程度、变形温度和变形速率对显微组织(放大倍数为2.8万倍)分形维数的影响如图4所示。

由图4可以看出，变形温度和变形速率一定时，随着变形程度的增大，显微组织的分形维数增大。变形程度较小时，合金晶体中的位错密度也较小，且位错线大多长而直；随着变形程度的增加，位错之间相互交割加剧，具有更高密度的位错缠结，位错线长度因缠结而逐步缩短，显微组织形貌更加复杂，因而分形维数增大。

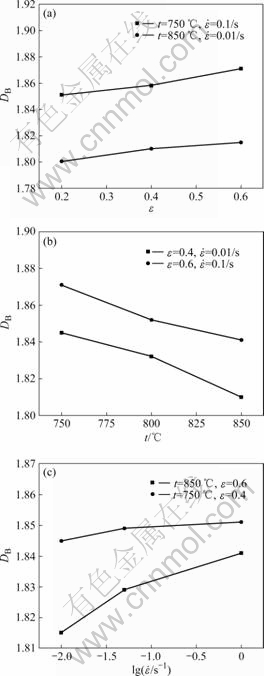
图4  变形参数对显微组织的分形维数的影响

Fig.4  Effects of deformation parameters on fractal dimension of microstructure: (a) D_B—ε curve; (b) D_B—t curve; (c) D_B—lg curve

当其它变形条件保持不变，随着变形温度的升高，显微组织的分形维数减小；变形温度较低时，位错密度较大且位错线短小；而变形温度较高时，由于热激活作用增强，原子扩散、位错交滑移、攀移和晶界迁移能力增加；且软化行为发生迅速，部分位错相互抵消，因而降低了位错的增殖率。位错密度减小，且位错线长而平直，显微组织的不规则程度减小，分形维数减小。

另外，当变形温度和变形程度一定时，显微组织的分形维数随着变形速率的减小而减小。变形速率较小时，位错密度增加速率小，且由于变形时间较长，原子扩散较充分，动态软化作用也较为充分，因而晶粒内部位错密度较小，分形维数减小。

不同变形参数下Ti-15-3合金的TEM像如图5所示。由图5可看出，位错密度越大，相应的显微组织分形维数也越大，此时，热变形过程中软化过程进行得越不充分。因此，为获得较好的显微组织，需减小显微组织的分形维数，即变形量一定时，适当提高变形温度和降低变形速度。

图5  不同变形参数下Ti-15-3合金的TEM像

Fig.5  TEM images of Ti-15-3 alloy deformed at different parameters: (a) t=750 ℃, ε=0.4, 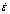=0.1/s; (b) t=750 ℃, ε=0.6, 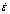=0.1/s; (c) t=850 ℃, ε=0.6, 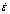=0.1/s

3.3  流变应力与分形维数间的关系

真应力－真应变曲线是材料内部组织性能变化的宏观表现，基体中平均位错密度越大，合金的流变应力就越大。图6所示为Ti-15-3合金热变形显微组织 (放大倍数为2.8万倍)的分形维数与材料的流变应力间的关系。由图6可以看出，在热变形过程中，流变应力越大，显微组织的分形维数也越大。为保证变形的顺利进行，也需要减小显微组织的分形维数，即在变形量一定时，适当提高变形温度和降低变形速度。

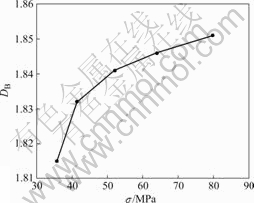
图6  热变形过程中Ti-15-3合金的显微组织分形维数与流变应力关系

Fig.6  Relationship between fractal dimension and flow stress of Ti-15-3 alloy during hot deformation

相对传统的、经验性的材料组织结构的定性分析而言，分形分析是对其开展的有实际意义的、定量化分析，为材料的力学性质和功能的分析提供了一种可能的分析手段。值得注意的是，采用不同的方法所测得的分形维数不同，但分形维数的变化规律和趋势是相同的。

4  结论

1) 同一显微组织在不同尺度下，位错的分布具有相似规律，表明Ti-15-3合金热塑性变形显微组织确实具有典型相似性和不规则性的分形特征，可以采用与尺度无关的分形维数对其进行定量描述。

2) 变形工艺参数通过影响显微组织演变而影响其分形维数。在当前的变形条件下，随着变形程度和变形速率增大以及变形温度的降低，显微组织的分形维数增大。

3) 流变应力增大，表征显微组织复杂程度的分形维数也增大。

REFERENCES

[1] PYUN S I, RHEE C K. An investigation of fractal characteristics of mesoporous carbon electrodes with various pore structures[J]. Electrochimcia Acta, 2004, 49(24): 4171?4180.

[2] RIBEIRO M F, HOROVISTIZ A L, JESUINO G A, HEIN O, ABBADE P, CRNKOVIC J. Fractal analysis of eroded surfaces by digital image processing[J]. Materials Letters, 2002, 56(4): 512?517.

[3] KUSIAK J, KUZIAK R. Modeling of microstructure and mechanical properties of steel using the artificial neural network[J]. Journal of Materials Processing Technology, 2002, 127: 115?121.

[4] AHMED H, WELLS M A, MAIJER D M, HOWES B J, WINDEN M R. Modelling of microstructure evolution during hot rolling of AA5083 using an internal state variable approach integrated into an FE model[J]. Mater Sci Eng A, 2005, 390: 278?290.

[5] RAFAEL C. On the variation of grain size and fractal dimension in an austenitic stainless steel[J]. Materials characterization, 2001, 46(5): 353?358.

[6] WAN F Y, YUAN Z D. Recognition and classification of metallography via fractional dimension[C]// Proceeding of the 4th World Congress on Intelligent Control and Automation. Shanghai: East China University of Science and Technology Press, 2002: 10?14.

[7] 龚宁峰, 王印培. 非金属夹杂物分形特征研究[J]. 机械工程材料, 2003, 27(4): 24?26.
GONG Ning-feng, WANG Yin-pei. The fractal characters of non-metal inclusions[J]. Materials for Mechanical Engineering, 2003, 27(4): 24?26.

[8] 王印培, 陈 进, 孙晓明. 珠光体球化的分形研究[J]. 理化检验—物理分册, 2003, 39(3): 129?132.
WANG Yin-pei, CHEN Jin, SUN Xiao-ming. Investigation on the fractal dimension of pearlite spheroidization[J]. Physical Testing and Chemical Analysis, Part A: Physical Testing, 2003, 39(3): 129?132.

[9] 李 平, 张廷安, 汪秉宏, 豆志河. 灰度阈值对图像分形特征参数提取的分析[J]. 东北大学学报, 2006, 27(1): 57?59.
LI Ping, ZHANG Ting-an, WANG Bing-hong, DOU Zhi-he. Grey level threshold used to extract fractal characteristic parameter of surface topography image[J]. Journal of Northeastern University, 2006, 27(1): 57?59.

[10] 曹 力, 史忠科. 金属图象分割的研究[J]. 航空材料学报, 2006, 26(1): 11?15.
CAO Li, SHI Zhong-ke. Studying to metal image segmentation[J]. Journal of Aeronautical Materials, 2006, 26(1): 11?15.

[11] KUZNETSOV P V, PANIN V E, SCHREIBER J. Fractal dimension as a characteristic of deformation stages of austenite stainless steel under tensile load[J]. Theoretical and Applied Fracture Mechanics, 2001, 35(2): 171?177.

[12] 彭瑞东, 谢和平, 鞠 扬. 二位数字图像分形维数的计算方法[J]. 中国矿业大学学报, 2004, 33(1): 19?24.
PENG Rui-dong, XIE He-ping, JU Yang. Computation method of fractal dimension for 2-D digital image[J]. Journal of China University of Mining & Technology, 2004, 33(1): 19?24.

[13] LOPEZ F M, VILCHEZ M A C, ALVAREZ R H. An improved method to estimate the fractal dimension of physical fractals based on the Hausdorff definition[J]. Physica A, 2001, 298(3/4): 387?399.

[14] ZAISER M, BAY K, HAHNER P. Fractal analysis of deformation-induced dislocation patterns[J]. Acta Materialia, 1999, 47(8): 2463?2476.

[15] HAHNER P, ZAISER M. Dislocation dynamics and work hardening of fractal dislocation cell structure[J]. Mater Sci Eng A, 1999, 272: 443?454.

基金项目：国家自然科学基金资助项目(50405020)

收稿日期：2008-02-14；修订日期：2009-01-12

通讯作者：李  萍，教授，博士；电话：0551-2901368；E-mail: cisi­_1314@126.com

(编辑 李艳红)