Temperature distribution in adiabatic shear band for ductile metal based on JOHNSON-COOK and gradient plasticity models

WANG Xue-bin(王学滨)

Department of Mechanics and Engineering Sciences, Liaoning Technical University, Fuxin 123000, China

Received 21 June 2005; accepted 11 November 2005

Abstract: Gradient-dependent plasticity considering interactions and interplay among microstructures was included into JOHNSON-COOK model to calculate the temperature distribution in adiabatic shear band(ASB), the peak and average temperatures as well as their evolutions. The differential local plastic shear strain was derived to calculate the differential local plastic work and the temperature rise due to the microstructural effect. The total temperature in ASB is the sum of initial temperature, temperature rise at strain-hardening stage and non-uniform temperature due to the microstructural effect beyond the peak shear stress. The flow shear stress—average plastic shear strain curve, the temperature distribution, the peak and average temperatures in ASB are computed for Ti-6Al-4V. When the imposed shear strain is less than 2 and the shear strain rate is 1 000 s^-1, the dynamic recovery and recrystalliza- tion processes occur. However, without the microstructural effect, the processes might have not occurred since heat diffusion decreases the temperature in ASB. The calculated maximum temperature approaches 1 500 K so that phase transformation might take place. The present predictions support the previously experimental results showing that the transformed and deformed ASBs are observed in Ti-6Al-4V. Higher shear strain rate enhances the possibility of dynamic recrystallization and phase transformation.

Key words: Ti-6Al-4V; adiabatic shear band; gradient-dependent plasticity; JOHNSON-COOK model; dynamic recrystallization; phase transformation

1 Introduction

Adiabatic shear localization is one of the most important deformation and failure mechanisms in some titanium alloys subjected to moderate and high shear strain rates. Adiabatic shear band(ASB) can be observed in various applications, such as metal forming, perforation, impact on structures, ballistic impact, machining, torsion, explosive fragmentation, grinding, interfacial friction, powder compaction and granular flow[1-15]. The formation of ASBs is often followed by ductile fracture.

The accurate assessment of the peak temperature in ASB is especially important in identifying whether dynamic recovery and recrystallization processes as well as phase transformation have occurred and in understanding the microstructures of ASB. The temperature and its evolution are usually assessed according to the measured stress-strain curve. Actually, only the average temperature was obtained, rather than the maximum value of non-uniform temperature. Some numerical predictions have presented temperature distributions and/or their evolutions[5-9]. However, once the traditional elastoplastic constitutive relations were adopted in finite element and finite difference methods, then the pathological mesh sensitivity cannot be overcome. On the aspect of experimental measurements, the array of infrared detectors was usually employed to measure the local temperature rise during the deformation process[1-4]. However, the actual peak temperature was inevitably underestimated since the observed area must have included some of the colder material to either side of the narrow ASB[1]. For example, the measured peak temperatures in ASB for Ti-6Al-4V were 723 K[3] and 823 K[2], respectively. Obviously, these temperatures have approached or reached temperatures of dynamic recovery and recrystallization processes. However, they were much lower than those of phase transformation. In fact, phase transformation has been confirmed by experimental tests[10, 11]. In addition, only the temperatures on the surface of material were measured, which could lower than those within the material due to the fact that the material on the surface was readily cooled. The distributions and evolutions of temperature as well as the effects of some parameters have been calculated based on gradient-dependent plasticity[16]. However, only linear strain-softening effect was taken into account.

The analytical derivation for the temperature distribution in ASB is extremely difficult if the strain-hardening effect is considered in JOHNSON- COOK model considering the effect of strain gradient. In the present paper, the numerical calculations are carried out. As an example, the flow shear stress-average plastic shear strain curve, the temperature distribution, the peak and average temperatures as well as their evolutions in ASB are computed for Ti-6Al-4V deformed at different shear strain rates.

2 JOHNSON-COOK model and initiation of shear localization

In JOHNSON-COOK Model[7, 15], the flow shear stress τ is given by

    (1)

where   is the average plastic shear strain, 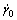is the reference shear strain rate,  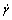is the imposed shear strain rate in dynamic shearing test, T₀ is the initial temperature, T_m is the melting temperature, the coefficients A, B, C, m and n are constitutive parameters, T is the present temperature dependent on T₀ and the plastic work done by shear stress. At the right hand side of Eqn.(1), the first term describes the effect of strain-hardening, the second term represents the instantaneous strain-rate sensitivity and the last term reflects the thermal-softening effect due to an increase of temperature in the process of plastic shear deformation. The present temperature T can be expressed as[7, 15]

                         (2)

where  ρ is the density, β is the work to heat conversion factor and is usually taken as 0.9, c_p is the heat capacity.

All of the needed parameters for many kinds of metals or alloys, such as A, B, C, m, n, T₀, T_m, 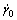, , ρ, β and c_p, can be found in literature. Thus, we can obtain the τ— curve through a numerical calculation. A schematic curve in monotonous loading is shown in Fig.1.

In Fig.1, γ_c is the critical plastic shear strain corresponding to the maximum value τ_max of flow shear stress. The occurrence of ASB is usually attributed to the thermal-plastic shear instability: the thermal softening due to the dissipation of part of the mechanical work just overcomes the strain-hardening effect. Therefore, the condition for onset of ASB is

                                    (3)

The analytical solution of γ_c cannot be found using Eqns.(1)-(3). However, it can be obtained by a numerical calculation if all of the parameters are known.

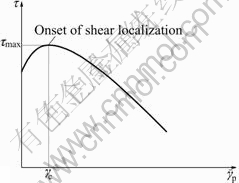
Fig.1 Relation between flow shear stress and plastic shear strain as well as initiation of shear localization

3 Analysis of ASB based on gradient- dependent plasticity

3.1 Differential local plastic shear strain in ASB

In the paper, ASB is considered to be a one-dimensional simple shear problem. ASB has a finite thickness or width w in y direction, whereas it is infinite in the shear direction x and in the out-of plane direction z, as shown in Fig.2. At the top and base of ASB, shear stress τ is uniform.

Fig.2 Schematic diagram of narrow ASB subjected to shear stress

The microstructural effect (interactions and interplay among microstructures) can be taken into account in terms of the so-called non-local theory where the non-local variable can be expressed as the weighted average of its local counterpart over a surrounding region. Gradient-dependent plasticity is a special case of the non-local theory and can be strictly derived[17-19].

Herein, we let the difference  be a non-local variable 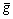. Thus,  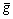and g(y) can be written as

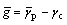                                 (4)

g(y)=γ_p(y)-γ_c                                 (5)

where  g(y) is the local variable of 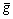, γ_p(y) is the local plastic shear strain. γ_c is not dependent on the coordinate y and is concerned with constitutive parameters and loading condition.

According to the non-local theory or gradient- dependent plasticity, 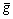 is expressed as

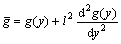                         (6)

where  l is the internal length parameter reflecting the heterogeneous extent of material texture, which is concerned with the grain size. For material with finer microstructures, it is lower.

The derivations for w and g(y) are similar to Refs.[17-19]. Thus, we have

w=2πl                                      (7)

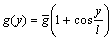                          (8)

Using Eqns.(4) and (5), we can obtain an expression for γ_p(y) as

              (9)

The differential local plastic shear strain dγ_p(y) can be written as using Eqn.(9)

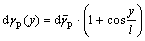                    (10)

3.2 Differential local temperature distribution due to microstructural effect

The differential local plastic work dW(y) due to the plastic shear deformation is

                           (11)

The differential temperature distribution dT_m(y) due to the microstructural effect is

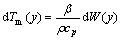                        (12)

Thus, we can present the local temperature distribution by integrating with respect to γ_p(y):

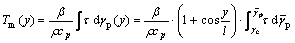    (13)

3.3 Temperature increase prior to pre-peak

The temperature distribution is uniform prior to the peak shear stress τ_max. The temperature increase T₁ at the pre-peak is given as

                         (14)

3.4 Total temperature distribution beyond occurrence of ASB

The total temperature distribution T(y) is the sum of initial temperature T₀, increment of temperature T₁ at strain-hardening stage and non-uniform temperature T_m(y) due to interactions and interplay among microstructures:

T(y)=T₀+T₁+T_m(y)                            (15)

4 Examples and discussion

According to Ref.[15], we assign the following values to various parameters for Ti-6Al-4V: A=418.4 MPa, B=394.4 MPa, C=0.035, m=1.0, n=0.47, T_m=1 932 K, ρ=4 430 kg/m³, T₀=300 K, 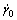=0.000 01 s^－1, c_p=564 J/(kg·K) and β=0.9. In addition, we select =1 000 s^－1. Using these parameters above, we can determine the value of the critical plastic shear strain γ_c and the maximum value of flow shear stress are about 0.77 and 1.05 GPa, respectively, by a numerical calculation.

Moreover, experimental observations[2] show that the thickness of ASB for Ti-6Al-4V is about 12-55 ?m. Thus, we can let w=20 ?m. The internal length parameter l is 3.18 ?m according to Eqn.(7).

The obtained numerical relation between flow shear stress and average plastic shear strain is shown in Fig.3. Fig.4 shows the distributions and evolutions of temperature in ASB for different average plastic shear strains. The three horizontal straight lines are the average values of non-uniform temperatures T(y) in ASB. It is found from Fig.4 that the average temperature increases with 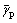. The profile of non-uniform temperature distribution becomes steeper as  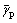increases and the peak temperature in ASB also increases. In addition, at the two edges of ASB, no temperature rise occurs beyond the onset of ASB.

The evolution of non-uniform temperature distribution shown in Fig.4 qualitatively agrees with the previously numerical results based on dislocation dynamics[5]. In addition, WANG[16] also presented the similar profile of non-uniform temperature distribution in ASB for different average plastic shear strains on the basis of linear strain-softening constitutive relation where gradient-dependent plasticity was introduced.

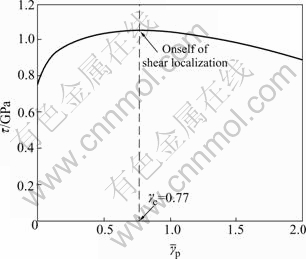
Fig.3 Relation between flow shear stress and average plastic shear for Ti-6Al-4V

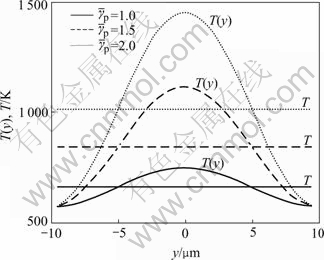
Fig.4 Uniform and non-uniform temperature in ASB for different plastic strains

Fig.5 shows the evolutions of the average and peak temperatures. Whether it is at pre-peak or not, both the average and peak temperatures increase slowly. Two kinds of curves overlap prior to the peak flow shear stress. Beyond the peak, the lower the flow shear stress is, the larger the difference between the two curves is.

It is known that the onset of dynamic recovery/recrystallization processes in metals generally occur at about 0.4-0.5 T_m, which is about 773-966 K for Ti-6Al-4V[2]. The upper bound of dynamic recovery/recrystallization processes has been marked in Fig.5. Obviously, the processes might just take place according to the flow shear stress-average temperature curve. However, if we only consider the shear stress- peak temperature curve, then the processes will take place unquestionably since the peak temperature has greatly exceeded 0.5 T_m. Moreover, it should be noted that the dynamic recovery/recrystallization processes only occur at the center of ASB, rather than the entire ASB. Experimental observations for many kinds of metals and alloys including Ti-6Al-4V have verified that dynamic recovery/recrystallization processes have occurred in ASBs so that the fine grains at the center of ASB have been observed.

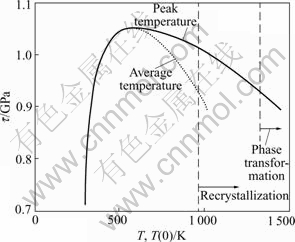
Fig.5 Relations between flow shear stress and average temperatures as well as peak temperature in ASB

We know that the temperature of phase transformation from (α+β) to β in Ti-6Al-4V is about   1 253-1 283 K[2]. The upper limit of 1 283 K is also marked in Fig.5. Apparently, when the flow shear stress is larger than 0.9 GPa (corresponding to the average plastic shear strain of 2), phase transformation cannot occur in terms of the average temperature. Whereas, if we consider the microstructual effect, then phase transformation might take place for the maximum temperature has approached 1 500 K. In fact, both trans- formed and deformed ASBs have been observed in Ti-6Al-4V by several researchers[10,11]. The present numerical predictions about maximum temperature in ASB support these experimental observations.

Fig.6 shows the three-dimensional temperature distribution within ASB, where y′=y+w/2. It can be seen that the distribution of temperature is uniform when 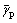 is less than γ_c(0.77). Afterwards, the onset of shear localization leads to the non-uniformity of temperature distribution in ASB, as cannot be predicted according to the classical elastoplastic theory where no internal length parameter is involved so that the microstructural effect cannot be taken into account.

Fig.7 shows the effect of strain rate on the relation between flow shear stress and peak temperature. It is indicated that higher imposed shear strain rate results in higher peak strength. At the same level of flow shear stress, higher shear strain rate leads to higher peak temperature in ASB. If the same peak temperature is reached, then Ti-6Al-4V deformed at higher shear strain rate is subjected to a higher level of flow shear stress.

Effect of the imposed shear strain rate on the non-uniform temperature distributions in ASB is shown in Fig.8 with 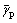=2. We can conclude that higher shear strain rate causes the profile of temperature distribution in ASB to be steeper and the peak temperature to be increased, as can also be seen from Fig.7. The present numerical prediction is consistent with the experimental observations by ZHOU et al[3]. They found that the maximum temperatures observed in ASBs increase monotonically with the impact velocity for Ti-6Al-4V. Higher speeds in Ref.[3] correspond to higher strain rates in the present paper.

Fig.6 Three-dimensional temperature distribution in ASB

Fig.7 Effect of imposed shear strain rate on relation between flow shear and maximum temperature

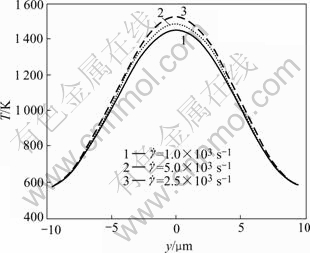
Fig.8 Effect of imposed shear strain rate on non-uniform temperature distribution in ASB

5 Conclusions

Gradient-dependent plasticity is included into JOHNSON-COOK model to calculate the distribution of temperature in ASB, the peak and average temperatures and their evolutions. Thus, the effects of strain-hardening, strain rate sensitivity, thermal-softening and strain-gradient or microstructure can be considered.

The total temperature in ASB is assumed to be the sum of initial temperature, increment of temperature at strain-hardening stage, and non-uniform temperature due to the interactions and interplay among microstructures.

It is found that when the imposed shear strain is less than 2 and the shear strain rate is 1 000 s^－1, the peak temperature for Ti-6Al-4V in ASB has greatly exceeded the upper bound temperature of dynamic recovery/ recrystallization processes. Accordingly, the dynamic recovery/recrystallization processes will occur undoubtedly. However, if we assess the average temperature in ASB to determine whether the processes take place, then the processes might have not occurred since the heat diffusion will decrease the average temperature in ASB. The calculated maximum value of temperature approaches 1 500 K, which is greater than the phase transformation temperature. As a result, phase transformation might take place. In fact, both transformed and deformed ASBs have been observed in Ti-6Al-4V by several researchers. The present numerical predictions about maximum temperature in ASB support these experimental observations.

Higher imposed shear strain rate results in higher peak temperature in ASB at the same level of flow shear stress and in steeper profile of temperature distribution in ASB. Thus, higher shear strain rate will enhance the possibility of dynamic recovery/recrystallization processes and phase transformation. The conclusion that higher shear strain rate leads to higher temperature in ASB agrees with the previously experimental measurements.

In addition, it should be noted that the present analysis is particularly applicable to the high strain rate tests, for heat diffusion is completely neglected.

References

[1] Hartley K A, Duffy J, Hawley R H. Measurement of the temperature profile during shear band formation in steels deforming at high strain rates[J]. J Mech Phys Solids, 1987, 35(3): 283-301.

[2] Liao S C, Duffy J. Adiabatic shear bands in a Ti-6Al-4V titanium alloy[J]. J Mech Phys Solids, 1998, 46(11): 2201-2231.

[3] Zhou M, Rosakis A J, Ravichandran G. Dynamically propagating shear bands in impact-loaded prenotched plates(I)—Experimental investigations of temperature signatures and propagation speed[J]. J Mech Phys Solids, 1996, 44(6): 981-1006.

[4] Dao K C, Shockey D A. A method for measuring shear-band temperature[J]. J Appl Phys, 1979, 50(12): 8244-8247.

[5] Klepaczko J R, Rezaig B. A numerical study of adiabatic shear banding in mild steel by dislocation mechanics based constitutive relations[J]. Mech Mater, 1996, 24(2): 125-139.

[6] YANG Yang, CHENG Xin-lin, AN Yu-long. Numerical simulation on adiabatic shearing behavior of TB2[J]. The Chinese Journal Nonferrous Metals, 2004, 14(5): 718-724.(in Chinese)

[7] DiLellio J A, Olmstead W E. Numerical solution of shear localization in JOHNSON-COOK materials[J]. Mech Mater, 2003, 35(3-6): 571-580.

[8] LI Shao-fan, LIU Wing-kam, QIAN Dong, GUDURU P R, ROSAKIS A J. Dynamic shear band propagation and micro-structure of adiabatic shear band[J]. Comput Methods Appl Mech Eng, 2001, 191(1-2): 73-92.

[9] BAI Y, BODD B. Adiabatic Shear Localization[M]. Oxford: Pergamon Press , 1992.

[10] XU Y B, MEYERS M A. Microstructural evolution of localized shear bands induced during explosion in Ti-6Al-4V alloy[J]. Journal of Materials Science and Technology, 2003, 19(5): 385-387.

[11] Me-Bar Y, Shechtman D. On the adiabatic shear of Ti-6Al-4V ballistic targets[J]. Mater Sci Eng, 1983, 58(2): 181-188.

[12] YANG Yang, XIONG Jun, YANG Xu-yue. Microstructure evolution mechanism in adiabatic shear band in TA2[J]. Trans Nonferrous Met Soc China, 2004, 14(4): 670-674.

[13] Xue Q, Meyers M A, Nesterenko V F. Self-organization of shear bands in titanium and Ti-6Al-4V alloy[J]. Acta Mater, 2002, 50(3): 575-596.

[14] Xu Y B, Wang Z G, Huang X L, XING D, BAI Y L. Microstructure of shear localization in low-carbon ferrite pearlite steel[J]. Mater Sci Eng A, 1989, A114(15): 81-87.

[15] Daridon L, Oussouaddi O, Ahzo S. Influence of the material constitutive models on the adiabatic shear band spacing: MTS, power law and JOHNSON-COOK models[J]. Int J Solids Struct, 2004, 41(11-12): 3109-3124.

[16] WANG Xue-bin. Calculation of temperature distribution in adiabatic shear band based on gradient-dependent plasticity[J]. Trans Nonferrous Met Soc China, 2004, 14(6): 1062-1067.

[17] WANG Xue-bin. Local and global damages of quasi-brittle material in uniaxial compression based on gradient-dependent plasticity[J]. Key Eng Mater, 2005, 293-294: 719-726.

[18] WANG Xue-bin, DAI Shu-hong, HAI Long, PAN Y S. Analysis of localized shear deformation of ductile metal based on gradient-dependent plasticity[J]. Trans Nonferrous Met Soc China, 2003, 13(6): 1348-1353.

[19] WANG Xue-bin, YANG Mei, YU Hai-jun, PAN Y S. Localized shear deformation during shear band propagation in Titanium considering interactions among microstructures[J]. Trans Nonferrous Met Soc China, 2004, 14(2): 335-339.

Foundation item: Project(2004F052) supported by the Educational Department of Liaoning Province, China

Corresponding author: WANG Xue-bin; Tel: +86-418-3351351; E-mail: wxbbb@263.net

(Edited by LONG Huai-zhong)