J. Cent. South Univ. (2012) 19: 572-577

DOI: 10.1007/s11771-012-1041-2

Critical weight on bit of double-driven bottomhole assembly during vertical and fast drilling

ZHU Xiao-hua(祝效华), JIA Yan-jie(贾彦杰), TONG Hua(童华)

College of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: It is difficult to determine the optimal weight on bit (WOB) of the double-driven bottomhole assembly (DD-BHA, with double stabilizers and a bent housing positive displacement motor (PDM)) which is employed during vertical and fast drilling. High WOB leads to well deviation out of control, and low WOB leads to low rate of penetration (ROP). So considering the rock physical properties, the anisotropy index function of polycrystalline diamond compact (PDC) bit was derived with the structure and cutting performance parameters of the bit, and the effect of natural hole deviation tendencies on the performance of DD-BHA resisting deviation was represented. The concept of elliptic deformation ratio was used to characterize the performance of DD-BHA resisting deviation. Eventually, a model calculating the critical WOB was established. By comparing the model predictions with the measured hole angle changes in the field, the results show that the model predictions are accurate with error less than 5.8%, which can meet the operational requirements in the projects. Furthermore, the model was adopted to justify and guide the operating conditions and parameters during drilling, which shows that the optimum WOB predicted by the model can not only control deviation but also improve ROP effectively. The model is independent on the formation characteristics of blocks, so it can be expanded widely to other oilfields.

Key words: double-driven bottomhole assembly; vertical and fast drilling; critical weight of bit; elliptic deformation ratio; bit anisotropy

1 Introduction

With the sustained and rapid development of the world economy, there have been severe and increasingly significant questions on the supply and demand of oil and gas, especially in China. Drilling is the main technology that explores geology and opens up the channels of oil and gas exploration and exploitation. Drilling quality and rate of penetration (ROP) directly affect the determination degree, the production and the input cost of oil and gas reserves. Considering the current status of drilling engineering, there are twenty thousands wells drilled every year in China, which is over 20% of the total number every year all over the world [1]. Controlling hole deviation and improving ROP are always two classic problems that influence the development of drilling engineering [2]. Hole deviation control has influence on drilling trajactory quality and geology hitting accuracy, and ROP has influence on drilling cost directly. Actually, hole deviation control will cause ROP sacrifice and maintaining a high ROP will result in hole angle out of limits. In future, the problems of hole angle and ROP will have more remarkable effects on the efficiency with deeper drilling and more difficult formations.

Recently, two kinds of means exist in the oilfield to resist hole deviation. One is positive and controls hole angle accurately but very costly, for example, vertical drilling system, straight-hole drilling device, VertiTrak, and PowerV; the other is a means of passive, including pendulum assembly, tower-type assembly, packed hole assembly, off-axis assembly and double-driven bottomhole assembly (DD-BHA). The passive methods have been used in vertical drilling extensively for their low cost. DD-BHA is developed most rapidly in recent years, consisting of a PDM (with a bent housing and double stabilizers) in conjunction with polycrystalline diamond compact (PDC) bit. It makes power by the rig floor and the motor at the bit. However, the effect of this means on resisting deviation is unstable [3-4] because of lacking of the systematic model that can scientifically describe its working mechanical characteristics, especially the calculation method of critical WOB has not been investigated and formed while the DD-BHA with double stabilizers and a bent housing PDM is employed during vertical and fast drilling. It is clear that the average ROP and hole angle for this drilling operation is most sensitive to high WOB values. Both ROP and deviating force would increase by running too much WOB, resulting in building hole angle rapidly. Drilling operation by too little WOB will induce drop hole angle and ROP, resulting in high drilling costs [5]. Therefore, according to the specific formation conditions and hole angle requirements in the target block, how to determine the optimal WOB is very important for improving the success rate of drilling inclined formations.

Since the first article about the drillstring statics by LUBINSKI was published in 1950, researchers have carried on many works on the stick-slip vibration of drillstring [6-7], buckling of drillstring [8-9], bit bounce [10-11] and so on. It is mainly excluded with respect to resisting deviation passively: FU et al [12] proposed the relation of drilling parameters with hole deviation by the off-axis assembly qualitatively; DI et al [13] compared the dynamic properties of pre-bending assembly and pendulum assembly, and PDM was not used in both assemblies; ZHAO et al [14] discussed all of the deviation problems encountered possibly during drilling and the solutions chosen by operators. However, the methods of calculation for critical WOB have no theoretical break through while employing the DD-BHA during vertical and fast drilling.

In this work, to establish the method of calculation for critical WOB while employing the DD-BHA during vertical and fast drilling, firstly the anisotropy coefficient model of PDC in conjunction with the DD-BHA was mathematically derived and validated, then the relationship between forces to resist deviation and natural formation deviation tendencies was built according to the rock anisotropy and technical characteristics of the DD-BHA during vertical and fast drilling. Eventually, a calculation model of critical WOB was established to improve the performance of DD-BHA resisting deviation systematically.

2 Mechanism of resisting deviation and model of critical WOB for DD-BHA

PDM is based on the Moineau principle and uses hydraulic power to provide drilling energy, independent of drillstring rotation. As the drilling fluid goes through a rotor/stator configuration, it generates additional centrifugal force that is transmitted to the bit, hereinafter called rotor centrifugal force. During the rotating drilling mode, the Stabilizer 2 on the PDM, called PDM-sta, prevents the bent housing PDM and adjacent drill tools from the wellbore as a fulcrum. The bent part of PDM between Stabilizer 1 and PDM-sta generates a centrifugal force under the combined function of eccentricity and revolutions of rotary table, called rotary table force. In terms of small borehole size, the DD-BHA bending deformation will be reduced, which decreases the bend angle. A portion of compressed hole wall supports the stabilizer and reacts with the PDM. This generates a continuous lateral force that acts on the bit as long as it contacts with the lateral rock. This lateral force, called geometry force, is characterized with an oriented rule as the rotary table force.

When rotor centrifugal force and rotary table force, due to the different amplitudes and directions, are combined, the resultant force transmits to bit through the leveraging of the PDM-sta. The resultant force gets effectively amplified because the leverage ratio of the upper section over PDM-sta to the lower section is greater than one. After amplified, it is combined with the higher geometry force to resist the natural hole deviation tendencies. That is called the resisting deviating force, representing the contribution of DD-BHA to natural hole deviation controlling. The DD-BHA model is shown in Fig. 1.

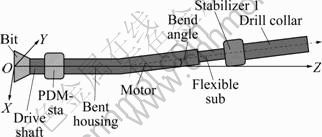
Fig. 1 DD-BHA model

2.1 PDC bit anisotropy index

The anisotropy index value is related to the variation in the cutting structure, and as such, it is impossible to be determined in the field based on visible geometric features [15]. In general, whether PDC bit or roller cone bit, the axial drillability is stronger than that of the lateral, namely the force and speed in every directional drilling are different. The anisotropy index I_b is represented as the bit anisotropy. The value of I_b is generally in the range of 0.001-0.1 for most PDC bits. Supposing the anisotropic bit drills in isotropic formation, bit axial force and speed are defined as F_a and V_a, and bit lateral force and speed are defined as F_l and V_l, respectively. So, the bit anisotropy index is given by

                                                              (1)

where 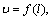 is the impact factor of gauge length [16]; the lateral drillability D_l is defined as the lateral displacement per bit revolution over the side force; D_l= V_l/|F_l|, m/(rad·N). The axial drillability D_a is the axial penetration per bit revolution over WOB, D_a=V_a/|F_a|, m/(rad·N).

Bits on various types and sizes have different anisotropy index values. As it is known, the anisotropy index can be measured by laboratory test, but it needs very high requirements to the measuring equipments. And there are many stochastic factors which affect the properties of the structures, such as manufacturing or curing processes. And the standardized geometry and loading in laboratory may be greatly different from those of actual structural components used in oilfield [17].  This will need a larger test cost resulted from PDC bit individuality. Therefore, bit companies seldom supply the anisotropy index by amount of laboratory tests. However, the anisotropy index by laboratory test cannot meet the engineering calculation accuracy. Therefore, this work focuses on the new method of calculating bit anisotropy index accurately, which starts from the bit model taking into account the three bit parts that interact with the formation－the cutting structure, the active gauge (trimmers or gauge cutters) and the passive gauge (gauge pad).

The bit anisotropy index is then a function of the axial drillability of the bit profile, the lateral drillability of the gauge cutters and the impact factor of gauge length, among which the drillability is related to the face profile, the gauge length, the cutter exploration height, the back rake and side rake angle [18].

The axial drillability of PDC bit can be simply approximated by

                                              (2)

As shown in Fig. 2 and Fig. 3, since the projection among cutters can be drawn [19], Eq. (2) may be written as

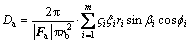                              (3)

and be simplified as

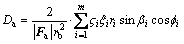                                (4)

where Δ_a is the axial effective cutting volume of  formation material by cutters on the face profile per second; r_b is the bit diameter; 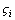 is defined as the exploration height of the i-th cutter; ξ_i is the width of the i-th cutter; r_i is the center distance between the i-th cutter and bit; β_i is the back rake angle of the i-th cutter; f_i is the side rake angle of the i-th cutter; m is the number of cutters.

The lateral drillability (D_l) is defined as the lateral effective cutting volume of formation material per second versus the side force, depending on the exploration height, back rake and side rake angle of the gauge cutters, as evaluated here. High lateral drillability for a bit implies a strong propensity for lateral deviation. This can be simply approximated by

     (5)

where Δ_l is the lateral effective cutting volume of formation material by gauge cutters per second;  is defined as the exploration height of the j-th gauge cutter; ξ_j is the width of the j-th gauge cutter; h_a is the gauge length; β_j is the back rake angle of the j-th gauge cutter; f_j is the side rake angle of the j-th gauge cutter; n is the number of gauge cutters.

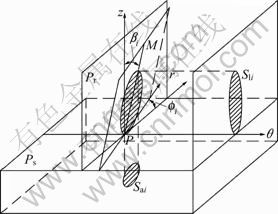
Fig. 2 Axial and lateral projections of i-th cutter or j-th gauge cutter

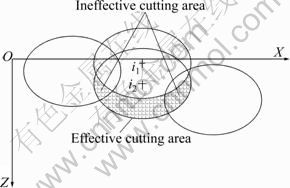
Fig. 3 Cutting area of i-th cutter or j-th gauge cutter

By substituting Eqs. (4) and (5) into Eq. (1), we find that

                           (6)

This is the calculation model of PDC bit anisotropy index.

2.2 Elliptic deformation ratio

The formation deviating force always keeps a specific direction that accords with the natural hole deviation tendencies. This force will make the direction of resisting deviating force offset towards its original direction, which is the main objective factor that causes the whole hole trajectory out of control. In some cases, the ratio of formation deviating force to resisting deviating force increases, and the offsetting tendency is sharper and the deviation is more severe. So the elliptic deformation ratio can be defined to characterize the effect of the formation deviating force on hole angle as follows:

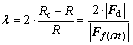                                               (7)

where R_c and R, as defined in Fig. 4, are the semi-major axis of the ellips and the radius of the envelop circle of the maximum resisting deviating force, respectively.

|F_d| is the formation deviating force [20] which can be calculated by

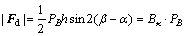                               (8)

where 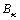 represents the formation deviating factor; P_B is the weight on bit.

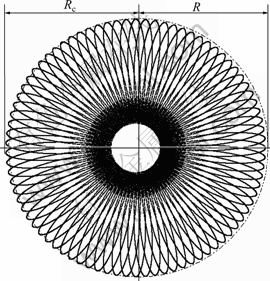
Fig. 4 Curve of steerable force during drilling by DD-BHA

The resisting deviating force is given by

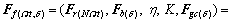
                           (9)

where 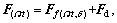 is the resultant force of formation deviating force and resisting deviating force, called the steerable force, and its amplitude curve can be seen in Fig. 4; F_r(NΩt) is the rotor force; N is the lobe of the rotor; Ωt is the rotation angular velocity of the rotor; F_b(Ωt) is the rotary table force; K is the leverage ratio, K=L₁/L₂; F_gc(δ) is the geometry force; δ is the virtual displacement parameter determined by outside diameter of stabilizer and inside diameter of borehole.

As depicted in Fig. 4, the periodic change of the resisting deviating force F_f(Ωt,δ) and the steerable force F_f(Ωt) were investigated theoretically. The frequency is N² times rotation angular velocity of rotary table. The shape of envelop, composed of maximum resisting deviating force F_f(Ωt,δ), is closer to a circle. In drilling isotropy formations without formation deviating tendency, the steerable force F_f(Ωt) and the resisting deviating force F_f(Ωt,δ) are converged. The DD-BHA offers the advantages of improving borehole quality and borehole trajectory and minimizing risk. However, in hard or steeply dipping formations and high natural hole deviation tendencies, the envelop of steerable force is not circular but approximatively elliptical. These formations are hard to be drilled vertically.

2.3 Calculation model of critical WOB

The DD-BHA can utilize its stronger preventing deviating tendency to effectively resist bit walk affected by the natural hole deviating force.

The natural formation deviating force drives bit towards drilling soft or unconsolidated formations. In terms of the elliptic deformation theory given hereinbefore, substituting Eq. (8) into Eq. (7) and simplifying, the formula for calculating hole angle can be obtained:

                                  (10)

To improve hitting the geological targets and reduce the difficulty of case running in, the actual hole angle should not exceed the engineering allowable value, that is,

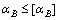                                                                   (11)

where 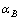 and  are the actual hole angle and the engineering allowable hole angle, respectively; I_b is the bit anisotropy index; λ is the elliptic deformation ratio; H_ψ is the difference of two measured depth.

Substituting Eqs. (7) and (10) into Eq. (9), it can be found that

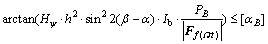    (11)

Taking the piecewise anisotropy of each hole section into consideration, the total hole angle can be presented as

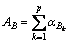                                                          (13)

where A_B and  are the total hole angle and hole angle of each hole section; p is the number of all measured depth points.

3 Engineering cases

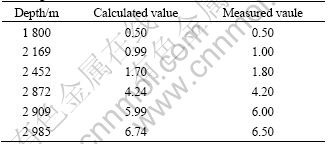
The model for calculating critical WOB could improve the performance of vertical and fast drilling in the anisotropic formation. It has been verified based on the JX-1 drilling operations, including actual well path, drilling parameters, rock characteristics and drilling assemblies (Table 1). Good comparison of calculated and measured values of hole angle is listed in Table 2. The maximum error is only 5.8%, under the threshold of engineering (15%). The model is reasonably accurate for prediction of critical WOB and completely meets engineering requirements.

Table 1 DD-BHAs and drilling parameters

Table 2 Comparison of calculated and measured values of JX-1 hole angle

The model was used for the adjustment and guidance to BX-4 and LX-1 drilling operations. BX-4 and LX-1 were both in process. Based on the drilling parameters of drilled interval and rock parameters of neighboring wells and BHA structures, the model had been developed to calculate the critical WOB in engineering allowable hole angle and makes a real-time adjustment of drilling operations to maximize ROP and limit hole angle below the threshold value.

The calculated and measured values of hole angle of the BX-4 and LX-1 are listed in Table 3. It is found that the maximum hole angles can be controlled within 3°, as shown in Fig. 5, and ROPs of the two wells are up to 40%-48% more than the neighbouring wells. The comparison of ROPs of the BZ-4 and the neighbouring wells is shown in Fig. 6.

Table 3 Comparison of calculated and measured values of cased hole angle (unit: °)

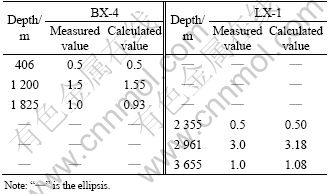
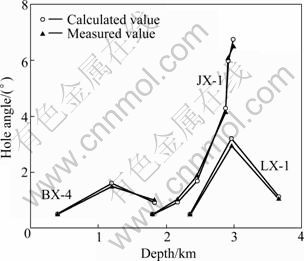
Fig. 5 Comparison of calculated and measured values of hole angles on different blocks

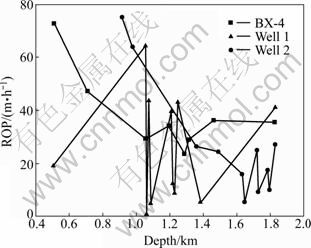
Fig. 6 Comparison of ROPs of BX-4 and neighbouring wells

4 Conclusions

1) The critical WOB is directly proportional to the resisting deviating force and the engineering allowable value of hole angle, and is inversely proportional to bit anisotropy index and natural formation deviating force. The increasing resisting deviating force will drop the elliptic deformation ratio and strengthen the performance of DD-BHA resistance to the formation of natural deviation. The bit walk tendency can be properly controlled, as required, so as to produce the desired drilling path.

2) The model has been applied in vertical and fast drilling in many blocks of CNOOC, by which hole angles are controlled ROPs are improved. The model does not depend on block characteristics, so it can be widely expanded to other oilfields.

Acknowledgement

A special thanks goes to CNOOC Energy Technology & Services Limited for the in-situ data.

References

[1] JIA Ping-jun, ZHENG Yi. Overview of CNPC drilling technology development [J]. Drilling & Production Technology, 2009, 32(1): 1-6. (in Chinese)

[2] WANG Hai-ge, SU Yi-nao. Progress of theoretical research on deviation control and drilling fast for vertical wells [J]. Acta Petrolei Sinica, 2004, 25(3): 86-90. (in Chinese)

[3] SHEN Zhong-hou, HUANG Hong-chun, GAO De-li. Analysis on new development and development trend of worldwide drilling technology [J]. Journal of China University of Petroleum: Edition of Natural Science, 2009, 33(4): 64-70. (in Chinese)

[4] BOUALLEG R, SELLAMI H, ROUABHI A, MENAND S. Effect of rocks anisotropy on deviation tendencies of drilling systems [C]// Proceedings of the 11th Congress of the International Society for Rock Mechanics. London: Taylor and Francis Group, 2007: 1221- 1224.

[5] SU Yi-nao, WANG Zheng-ying. Study of vertical drilling technology in high dip and application of BHA with offset axes sub [C]// Proceedings of SPE International Conference and Exhibition. Beijing: Society of Petroleum Engineers, 1998: 145-152.

[6] WU Sean Xian-ping, PAEZ L, PARTIN U, AGNIHOTRI M. Decoupling stick-slip and whirl to achieve breakthrough in drilling performance [C]// Proceedings of the SPE IADC/SPE Drilling Conference and Exhibition. New Orleans, Louisiana, USA: Society of Petroleum Engineers, 2010: 1-13.

[7] WU Sean Xian-ping, PAEZ L, PARTIN U, AGNIHOTRI M, TECUNDLOGJES S. Decoupling stick-slip and whirl to achieve breakthrough in drilling performance [J]. SPE International Oil and Gas Conference and Exhibition in China, 2-6 November 1998, Beijing, China, 2010.

[8] TAN Mei-lan, GAN Li-fei. Equilibrium equations for non linear buckling analysis of drill-String in 3D curved well-bores [J]. Sci China Ser E-Tech Sci, 2009, 52(3): 590-595.

[9] MITCHELL R F. Tubing buckling-The state of the art [J]. SPE Drilling & Completion (SPEDC). 2008, 9(1): 361-370.

[10] DYKSTRA M W, NEUBERT M, HANSON J M, MEINERS M J. Improving drilling performance by applying advanced dynamics models[C]// Proceedings of the SPE/IADC Drilling Conference. Amsterdam, Netherlands: Society of Petroleum Engineers, 2001: 1-18.

[11] LIU Mu-feng, PENG Zhen-bin, WANG Jian-jun, PENG Wen-xiang. Mechanism of mud job and rotary drilling technology in sand and gravel [J]. Journal of Central South University: Science and Technology, 2010, 41(1): 265-271. (in Chinese)

[12] FU Jian-hong, SHI Tai-he, XU Xue-jun, HE Wei-bing, YU Cheng-shui. Dynamic analysis of bottom hole assembly with eccentric sub and its motion simulation research [J]. Natural Gas Industry, 2004, 24(12): 65-68. (in Chinese)

[13] DI Qin-feng, ZHU Wei-ping, YAO Jian-lin, ZHOU Hai-yang. Dynamic model of bottom hole assembly used in pre-bending dynamic vertical and fast drilling technology [J]. Acta Petrolei Sinica, 2007, 28(6): 118-121. (in Chinese)

[14] ZHAO Jin-hai, LI Zi-feng, ZHANG Gui-lin, TANG Dai-xu. A preliminary study on dynamic influencing factors for bottom-hole assembly with bending angle or bias axis [J]. Rock and Soil Mechanics, 2003, 24(s1): 392-394. (in Chinese)

[15] HO Hwa-Shan. Method and system of trajectory prediction and control using PDC bits [P]. United States Patent: 5456141. 1995-10- 10.

[16] MENAND S, et al. How bit profile and gauges affect well trajectory [J]. SPE Drilling & Completion, 2003, 18(1): 22-32.

[17] HUANG Li-xin, XIANG Zhi-hai, SUN Xiu-shan, LIU Ying-hua, CEN Zhang-zhi. Optimal measurement placement for the material parameter identification of orthotropic composite plate with a hole [J]. Engineering Mechanics, 2006, 23(10): 30-34. (in Chinese)

[18] GONG Sheng-wu, ZHAO Fu-jun. Failure analysis of polycrystalline diamond compact cutters for breaking rock by bending waves theory [J]. Journal of Central South University of Technology, 2008, 15(1): 112-116.

[19] XIA Yi-min, BU Ying-yong, TANG Pu-hua, ZHOU Zhi-jin, MA Zhi-guo. Modeling and simulation of crushing process of spiral mining head [J]. Journal of Central South University of Technology, 2006, 13(2): 171-174.

[20] IBRAHIM A A, MUSA T A. Sudan-unity oil field fonuation force and bit profile effects on the well traject [J]. Journal of Applied Sciences 2004, 4(1): 58-63.

(Edited by HE Yun-bin)

Foundation item: Projects(50804040, 51004082) supported by the National Natural Science Foundation of China

Received date: 2011-04-29; Accepted date: 2011-09-13

Corresponding author: ZHU Xiao-hua; Tel: +86-13980020787; E-mail: zxhth113@163.com