
J. Cent. South Univ. (2019) 26: 3388-3396
DOI: https://doi.org/10.1007/s11771-019-4261-x

Evolution trend analysis of urban residents’ low-carbon travel development based on multidimensional game theory
WU Xiao-hui(武晓晖), HE Mei-ling(何美玲), CAO Shu-chao(曹淑超), SHI Yu-ji(施榆吉)
School of Automobile and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: In the travel process of urban residents, travelers will take a series of activities such as imitation and exclusion by observing other people’s travel modes, which affects their following trips. This process can be seen as a repeated game between members of the travelers. Based on the analysis of this game and its evolution trend, a multi-dimensional game model of low-carbon travel for residents is established. The two dimensional game strategies include whether to accept the low-carbon concept and whether to choose low-carbon travel. Combined with evolutionary game theory, the low-carbon travel choices of residents in different cities are simulated, and the evolutionary stability strategies are obtained. Finally, the influences of the main parameters of the model on the evolution process and stability strategies are discussed. The results show that travelers would develop towards two trends. Cities with more developed public traffic system have a higher proportion of receiving low-carbon concept and choosing low-carbon travel. Cities with underdeveloped public transport system could increase this proportion by some measures such as encouraging residents to choose slow transport and increasing the propaganda of low-carbon travel, but the positive effects of the measures like propaganda have a limited impact on the proportion.
Key words: low-carbon travel; evolution trend; multidimensional game; travel modes
Cite this article as: WU Xiao-hui, HE Mei-ling, CAO Shu-chao, SHI Yu-ji. Evolution trend analysis of urban residents’ low-carbon travel development based on multidimensional game theory [J]. Journal of Central South University, 2019, 26(12): 3388-3396. DOI: https://doi.org/10.1007/s11771-019-4261-x.
1 Introduction
Due to the global warming caused by the massive emissions of greenhouse gases, human beings face the challenge of increasing temperature, which is recognized by the international community as an environmental issue. China’s total GDP in 2017 reached US$12.7 trillion, making it the world’s largest developing country and the second largest economy in the world. According to the latest data released by CAIT Climate Data Explorer, China is the world’s largest country of greenhouse gas carbon dioxide emissions, accounting for 26.83% of the total emissions, exceeding the second-ranked US 12.47 %. Therefore, there is a huge pressure on the international community to reduce carbon emissions. In the People’s Republic of China First Biennial Update Report on Climate Change issued by the Chinese government in December 2016, energy activities account for 78.5% of China’s carbon emissions, while energy industry, manufacturing and construction, and transportation are the top three sources of carbon emissions. The total carbon emissions of the transportation are 788625 Gg, and the carbon emissions from road transportation account for 65.21% [1].
Cities with dense road networks are the key areas for carbon emissions from road transport. Therefore, low-carbon travel of urban residents is an important part of low-carbon transportation and a hot spot in current research. The research focuses on the influence factors of low-carbon travel using methods such as planned behavior theory, multivariate statistical analysis, and consumer choice theory [2-4], and how these factors affect low-carbon travel decisions [5]. The results show that low-carbon travel is the result of the active choice of travelers influenced by psychological factors. On the other hand, it is affected by objective factors such as travel time, travel expenses and comfort. Travelers of different genders, ages and incomes have different characteristics [6, 7]. According to the above research, the essence of the low-carbon travel problem is a process in which travelers choose high-carbon or low-carbon travel by judging their payoffs based on various factors. This is in line with the three elements of players, strategies and payoffs in game theory, so travelers can achieve certain equilibrium through repeated games of the choice of travel modes. At the same time, the influence factors and travel mode choices are no longer regarded as simple causal relationships but are mutually influential, and then conclusions closer to the actual situation could be obtained.
Game theory originated in the early 20th century. NEUMANN et al [8] proved the basic principles of game theory and established the discipline of game theory. Then he and NASH [9] laid the foundation for the development of subsequent game theory. Game theory in this period mainly studied the decision-making of the interaction of decision-making bodies in economics, and the equilibrium problem of such decisions. In 1994, the Nobel Prize in Economics was awarded to John F. Nash, John C Harsanyi and Reinhard Selten, who made outstanding contributions in the field of game theory [10, 11]. Since then, the use of game theory to study traffic strategies and equilibrium has begun to receive the attention of scholars. In terms of intersection, research focuses on how individual interactions affect the evolutions of strategies and how such evolutions can lead to changes in efficiency or safety. Some of these intersections have signal control [12, 13], some have no signal control [14-16], and can even be based on future vehicle networking intelligent controllers [17, 18]. In terms of travel path, the goal of the route selection strategy in the traffic network is to achieve favorable equilibrium, and to study the choice of the traffic participants in the traffic network and its evolution trend [19-21]. A more common approach for this type of problem is to use a hybrid stochastic equilibrium model to obtain a path selection solution through an iterative algorithm [22-24]. In terms of road network optimization and planning, it is regarded as a game between two or more parties. The equilibrium solution of the game determines the steady-state behavior of the network, and the basic characteristics of urban road network evolution are simulated by the model [25-27]. In terms of transportation mode selection, most of the research focuses on the use of evolutionary game theory [28], which treats travelers as bounded rationality and achieves the game equilibrium of travel modes through the method of trial and error [29, 30].
In summary, the game theory fits the characteristics of urban residents’ low-carbon travel research, and has a wide range of applications in the transportation field. Related research provides a reference for the construction of residents’ low- carbon travel model. The problem of low-carbon travel is essentially the choice of travel modes, but the low-carbon factor of travel has its particularity. It is not like travel time and costs, which has always existed objectively with travel. Whether the travelers accept the low-carbon concept is judged before analyzing the impact of the low-carbon factor on their travel. At the same time, after the travelers choose the travel modes multiple times, the attitude of the travel individual to the low-carbon concept may change, which makes it difficult to investigate in the same way as other factors. Therefore, after considering the low-carbon factor, the dimension that affects the choice of travel modes has increased. The traditional methods of selecting travel modes can only make a new game by adjusting the payoffs [31], and there are limitations in multi-domain decision-making. Multidimensional game theory can better match the characteristics of low carbon travel mentioned above.
2 Context
2.1 Low-carbon and high-carbon travel
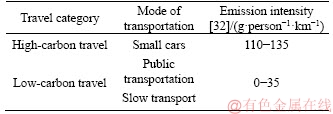
It is generally believed that low-carbon travel is carried out by means of transportation with lower per capita carbon emissions. Therefore, the modes of transportation in the city are divided into three categories: public transportation, small car and slow transport categories. Public transportation includes subways, light rails, regular buses, etc. Small cars include private cars, taxis, etc. Slow transport categories include electric vehicles, bicycles and walking. These cover most of the current transportation methods in cities, China. Through data retrieval, it can be found that the emission intensity of public transportation and personal slow traffic is much lower than that of small cars. Therefore, the categories of high-carbon travel and low-carbon travel are classified as Table 1.
Table 1 Categories of high-carbon and low-carbon travel
2.2 Traffic characteristics of different cities and analysis of low-carbon travel
With the emergence of new traffic modes, the development of urban traffic is becoming more diversified. In large cities, subways and light rails are relatively common, and they play a key role in public transportation. Urban rail transit has laid a solid foundation for the development of low-carbon travel. These cities can be divided into two categories: cities with large and mature road network (such as Shanghai), and the remaining with small and immature road network (such as Suzhou). In these cities, what different trends will residents’ low-carbon travel move toward? In guiding the residents to choose low-carbon travel, what is the difference in focus? These issues are worthy of consideration.
In medium-sized cities, the operation of BRT has a positive effect on the improvement of public traffic volume and service level. However, most medium-sized and small cities have only bus transit, such as Taizhou, China. According to existing policies and urban conditions, it is difficult for them to build subway, light rail and even BRT. Can these cities achieve the balance of low-carbon travel with the behavior of public traffic? Whether the proportion of public traffic in Urban Comprehensive Transportation Planning of the government can theoretically be realized? These issues are also concerned problem in low-carbon travel research.
In the following discussion, the evolution trend and characteristics of urban residents’ low-carbon travel under these traffic conditions will be studied.
3 Methods and model
Multidimensional game theory and evolutionary game theory models were used to describe the traveler’s choices of travel modes under the influence of low-carbon factor. The traveler’s choices were divided into two dimensions of choosing the travel modes and choosing whether to accept the low-carbon concept, and then the corresponding payoff functions were obtained. In the case of incomplete information, the evolutionary stability strategy of the game was obtained by the accumulation of relative advantages when some travel strategies were adopted. These issues are also concerned problem in low-carbon travel research.
3.1 Multidimensional game model
A game in which players choose their own maximum payoff based on a strategy vector composed of several aspects of the strategy is called a multidimensional game [33]. There are n players playing in m (m≥2) aspects at the same time. The selection space of player i is an m-dimensional space Si1×Si2×…×Sim, and the collection of strategy is (Si1, Si2, …, Sim), (Si1, Si2, …, Sim) Si1×Si2×…× Sim. The player’s payoffs are expressed as Ui{S11, S12, …, S1m}, …, (Si1, Si2, …, Sim), …, (Sn1, Sn2, …, Snm)}. In the process of urban residents’ low-carbon travel development, the low-carbon concept can not only be regarded as a factor in the choice of travel modes, but as the two aspects of mutual relationship. In other words, the choice of travel modes will also play a role in whether travelers receive low-carbon concepts. When travelers choose between the two aspects, their payoffs will also change accordingly, and the changes will counteract their following choices until certain equilibrium is reached. This is a multi-domain repeated game process, which fits well with the use of multidimensional game theory. In order to study the equilibrium of this game and its convergence characteristics, the low-carbon mode of travel strategy could be recorded as L, and the high-carbon mode of travel strategy as H. The strategy of receiving the low-carbon concept was denoted as R, and the strategy of rejecting the low-carbon concept was recorded as D. The travelers were divided into two indifferent groups I and II. If both I and II choose high-carbon travel, then the payoffs were (E, E). If group I chooses low-carbon travel and II chooses high-carbon travel, the payoffs were (G, J) and the opposite situations were (J, G). If both I and II choose low-carbon travel, the payoffs were (F, F). These payoffs were called traditional payoffs including travel time, cost, comfort, etc. Travelers accepted low-carbon concept and chose low-carbon travel to generate psychological payoff α (α>0). If they chose high-carbon travel, the psychological cost increased α. Rejecting the low-carbon concept has no effect on traditional payoffs. The payoffs matrix is shown in Table 2.
Si1×Si2×…× Sim. The player’s payoffs are expressed as Ui{S11, S12, …, S1m}, …, (Si1, Si2, …, Sim), …, (Sn1, Sn2, …, Snm)}. In the process of urban residents’ low-carbon travel development, the low-carbon concept can not only be regarded as a factor in the choice of travel modes, but as the two aspects of mutual relationship. In other words, the choice of travel modes will also play a role in whether travelers receive low-carbon concepts. When travelers choose between the two aspects, their payoffs will also change accordingly, and the changes will counteract their following choices until certain equilibrium is reached. This is a multi-domain repeated game process, which fits well with the use of multidimensional game theory. In order to study the equilibrium of this game and its convergence characteristics, the low-carbon mode of travel strategy could be recorded as L, and the high-carbon mode of travel strategy as H. The strategy of receiving the low-carbon concept was denoted as R, and the strategy of rejecting the low-carbon concept was recorded as D. The travelers were divided into two indifferent groups I and II. If both I and II choose high-carbon travel, then the payoffs were (E, E). If group I chooses low-carbon travel and II chooses high-carbon travel, the payoffs were (G, J) and the opposite situations were (J, G). If both I and II choose low-carbon travel, the payoffs were (F, F). These payoffs were called traditional payoffs including travel time, cost, comfort, etc. Travelers accepted low-carbon concept and chose low-carbon travel to generate psychological payoff α (α>0). If they chose high-carbon travel, the psychological cost increased α. Rejecting the low-carbon concept has no effect on traditional payoffs. The payoffs matrix is shown in Table 2.
Table 2 Multidimensional game payoffs matrix

3.2 Evolutionary game model
Evolutionary game theory assumes that the players are randomly drawn from the large population, and they repeatedly play the game in a biological or social way. The trend of residents’ choice of travel modes under the low-carbon concept can be analyzed by evolutionary game theory. In Table 2, let x, y, z and (1-x-y-z) be the proportion of the travelers which selected (H, D), (H, R), (L, D) and (L, R) strategy respectively, so the expected payoffs were u1, u2, u3, u4:

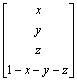 (1)
(1)
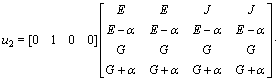
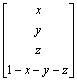 (2)
(2)
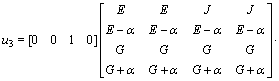
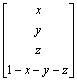 (3)
(3)

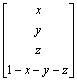 (4)
(4)
The average payoffs of the group are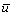 :
:

 (5)
(5)
The dynamic equations of the game are as follows:
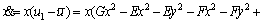
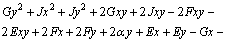
 (6)
(6)

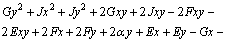
 (7)
(7)
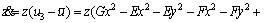

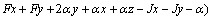 (8)
(8)
When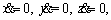 the nonlinear differential equation has singularities. Combined with the actual traffic significance, a stable singularity should be found in the following equation:
the nonlinear differential equation has singularities. Combined with the actual traffic significance, a stable singularity should be found in the following equation:
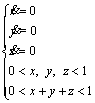 (9)
(9)
Let θ=Gx2-Ex2-Ey2-Fx2-Fy2+Gy2+Jx2+Jy2+2Gxy+2Jxy-2Fxy-2Exy+2Fx+2Fy+2αy+Ex+Ey-Gx-Gy+αx-2Jx-2Jy+αz-F+J, Eqs. (5) and (6) could be expressed as:
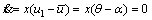 (10)
(10)
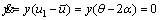 (11)
(11)
Obviously, (θ-α) and (θ-2α) are not equal to 0 simultaneously. Therefore, x and y have at least one of zero at the singularity of the differential equation. Therefore, at least one of x and y is equal to 0 at the singularity of the differential equation. The strategy (H, R) is the relative disadvantage of the strategy (H, D), so y=0. In the same way, z=0 could be obtained by comparing 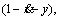
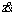 and
and  of the replication dynamic equations of the latter three strategies. In other words, the steady states of low-carbon travel trends of urban residents are moving toward (H, D) and (L, R) strategies. However, it is very complicated to analyze the stability of singular points through 3×3 partial derivative matrix under condition (9). Therefore, Table 2 is simplified to Table 3, and then the singularity stability is analyzed by parameter calibration and computer simulation.
of the replication dynamic equations of the latter three strategies. In other words, the steady states of low-carbon travel trends of urban residents are moving toward (H, D) and (L, R) strategies. However, it is very complicated to analyze the stability of singular points through 3×3 partial derivative matrix under condition (9). Therefore, Table 2 is simplified to Table 3, and then the singularity stability is analyzed by parameter calibration and computer simulation.
The expected payoffs when players I chooses (H, D), (L, R) are u11, u12:
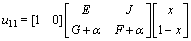 (12)
(12)
Table 3 Simplified payoffs matrix

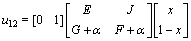 (13)
(13)
The average payoffs of the group are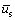 :
:
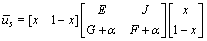 (14)
(14)
The dynamic equations of the game are as follows:
 (15)
(15)
4 Simulation and analysis
Let  in Eq. (4). Then the model
in Eq. (4). Then the model
parameters are calibrated, and the evolutionary stability strategy of the game is obtained through computer simulation.
4.1 Parameter calibration and simulation results
According to the previous analysis of the characteristics of different traffic conditions, Shanghai, Suzhou and Taizhou, China are selected as representatives of different types of cities as reference for parameter calibration. The basic traffic conditions of each city are captured from sources such as Gaode Map Traffic Big Data and Didi drip Big Data, as shown in Table 4.
Table 4 Comparison of urban basic traffic data
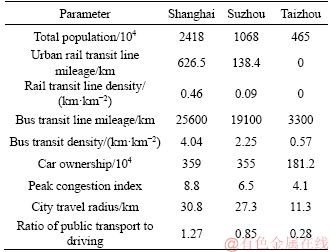
According to whether the travelers accepted the low-carbon concept and chose low-carbon travel, the corresponding scenarios of these three cities are established respectively. Referring to the data in Table 4, E, F, G and J are compared by adopting scenario analysis. High, medium and low are used to describe the relative relationship of their values. The results are shown in Table 5.
Table 5 Comparison of different city parameters

The low-carbon psychological payoff α should not be larger than the traditional payoffs so the magnitude of α should be smaller than E, F, G and J. E and F are the payoffs of everyone choosing low-carbon or high-carbon travel, and should be less than the payoffs G and J after crowd diversion. Therefore, without loss of generality, let 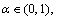
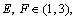
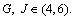 α1=0.2 and α2=0.8 are used to represent low and high estimates of psychological payoff. Combined with Table 5, three types of cities are assigned as follows, and the simulations are shown in Figures 1-3.
α1=0.2 and α2=0.8 are used to represent low and high estimates of psychological payoff. Combined with Table 5, three types of cities are assigned as follows, and the simulations are shown in Figures 1-3.
1) E=1, F=3, G=6, J=5, a1=0.2, a2=0.8;
2) E=1, F=2, G=5, J=5, a1=0.2, a2=0.8;
3) E=2, F=2, G=5, J=6, a1=0.2, a2=0.8.
4.2 Analysis of low-carbon travel evolution based on simulation results
The simulation results converge to a solution with practical traffic significance, and have proven to be feasible after being tested in Eq. (9). Considering the slow transport in low-carbon travel and comparing the simulation results with the ratio of public transport to driving in Table 5, it can be verified that the simulation results have a good match with the actual situation.

Figure 1 Low-carbon travel trends in Shanghai-type cities

Figure 2 Low-carbon travel trends in Suzhou-type cities

Figure 3 Low-carbon travel trends in Taizhou-type cities
It can be seen from Figure 1 that in Shanghai-type cities, the proportion (1-x) of travelers who accept low-carbon concept and choose low-carbon travel after repeated games will gradually converge to a high value. Under this condition, if the psychological payoff of low-carbon travel is increased from α1 to α2, the proportion of choosing low-carbon travel would further increase within a certain range. Figures 2 and 3 show that the proportion of low-carbon travel in Suzhou-type cities is lower than Shanghai-type cities, while the proportion in Taizhou-type cities is even lower. There is no urban rail transit in the Taizhou-type cities, and the proportion of travelers choosing private cars or taxis is more likely to reach a higher value. Urban residents are more inclined to reject the low-carbon concept.
Comparing Figures 1-3, it can be found that no matter which type of city, the improvement of low-carbon psychological payoff of travelers would have a positive impact on low-carbon travel, but this impact is relatively limited from the convergent results. The decisive influence on the result is the values of E, F, G and J. The higher value of F and G or the lower value of E and J, the higher proportion of travelers receiving the low-carbon concept and choosing low-carbon travel. The values of F, G, E and J basically reflect the comprehensive traffic conditions of city’s low-carbon travel and high-carbon travel, respectively. Combined with Table 5 for analysis, for Shanghai-type cities, there is little space for change in E, F, G and J. To achieve the goal of increasing the proportion of low-carbon travel, increasing the psychological payoff of low-carbon travel should be the main choice. Increasing the promotion of low-carbon travel is a common means of improving this psychological payoff. At present, the traffic policies implemented in Shanghai, such as restrictions on the travel of vehicles from other places and auction of private car licenses, have increased the restrictions on the traffic areas and total number of vehicles. Under this policy, the values of E and J are reduced, which is conducive to travelers receiving low-carbon concept and choosing low- carbon travel. Suzhou-type cities can also raise the values of F and G by improving the rail transit network, and move closer to the higher proportion of low-carbon travel. However, the Taizhou-type cities seem unable to establish a rail transit network. The main way to increase the values of F and G is to improve the existing conventional bus system. However, Taizhou’s traffic radius is the smallest, and the applicability of slow transport is extensive. The advantage of slow transport could make another contribution to raise the values of F and G, which is beneficial for the development of low-carbon transportation. Cities of this type need to be more cautious in developing traffic policies. For example, if the policy of restricting electric bicycles issued by Shenzhen is implemented in Taizhou-type Cities, the values of F and G will be further reduced, which means more difficult to achieve a higher proportion of low- carbon travel. As another example, the policies mentioned above such as the auction of private car licenses in Shanghai are beneficial to reduce the value of E and J. However, whether this kind of traffic policies is applicable to Taizhou, which has the least car ownership, is worth further discussion.
It is also worth noting that the higher the proportion of low-carbon travel is, the longer the iteration time is. Therefore, no matter what policies are adopted, promoting the development of low-carbon travel might be a relatively slow process.
5 Conclusions
Different from the usual consideration of low-carbon as a factor of travel modes choice, multidimensional game is used to study the problem of decision making in two dimensions of travel modes and low-carbon concept. Combined with the evolutionary game, the strategies (H, D) and (L, R) are evolutionary stability strategies among the four strategies composed of two dimensions. The simulation results show that the low-carbon concept has a certain positive effect on travel, but the decisive factors are mainly the conditions of the urban traffic system. The conditions of different urban traffic systems have different values of traditional payoffs and have an impact on the proportion of low-carbon travel. Moreover, the impact of transportation policies on low-carbon travel in different cities is analyzed, which could provide a reference for traffic policies making in these cities.
In general, this is a relatively macro-level study of low-carbon travel mainly based on the city’s traffic conditions. The future research direction is to refine the classification of travelers and influence factors, and to establish models from a more microscopic perspective to study the game of travelers in complex environments.
References
[1] LIU Zhao, LI Ling, ZHANG Yue-jun. Investigating the CO2emission differences among China’s transport sectors and their influencing factors [J]. Natural Hazards, 2015, 77(2): 1323-1343. DOI:10.1007/s11069-015-1657-2.
[2] LIU Di-yi, DU Hui-bin, SOUTHWORTH F, MA Shou-feng. The influence of social-psychological factors on the intention to choose low-carbon travel modes in Tianjin, China [J]. Transportation Research Part A: Policy and Practice, 2017, 105: 42-53. DOI: 10.1016/j.tra.2017.08.004.
[3] SCHWANEN T, BANISTER D, ANABLE J. Rethinking habits and their role in behaviour change: The case of low-carbon mobility [J]. Journal of Transport Geography, 2012, 24: 522-532. DOI: 10.1016/j.jtrangeo.2012.06.003.
[4] JING Peng, ZHAO Meng-yuan, HE Mei-ling, CHEN Long. Travel mode and travel route choice behavior based on random regret minimization: A systematic review [J]. Sustainability, 2018, 10(4): 1185. DOI: 10.3390/su10041185.
[5] JIA Ning, LI Li-ying, LING Shuai, MA Shou-feng, YAO Wang. Influence of attitudinal and low-carbon factors on behavioral intention of commuting mode choice–A cross-city study in China [J]. Transportation Research Part A: Policy and Practice, 2018, 111: 108-118. DOI: 10.1016/ j.tra.2018.03.010.
[6] MARSDEN G, MULLEN C, BACHE I, BARTLE I, FLINDERS M. Carbon reduction and travel behaviour: Discourses, disputes and contradictions. in governance [J]. Transport Policy, 2014, 35: 71-78. DOI: 10.1016/ j.tranpol.2014.05.012.
[7] GENG Ji-chao, LONG Ru-yin, CHEN Hong, LI Qian-wen. Urban residents’ response to and evaluation of low-carbon travel policies: Evidence from a survey of five eastern cities in China [J]. Journal of Environmental Management, 2018, 217: 47-55. DOI: 10.1016/j.jenvman.2018.03.091.
[8] NEUMANN J V. Zur theorie der gesellschaftsspiele [J]. Mathematische annalen, 1928, 100(1): 295-320. DOI: 10.1007/BF01448847. (in German)
[9] NASH J F. Equilibrium points in N-person games [J]. Proceedings of the National Academy of Sciences of the United States of America, 1950, 36(1): 48-49. DOI: 10.2307/88031.
[10] HARSANYI J C. Games with randomly disturbed payoffs: A new rationale for mixed-strategy equilibrium points [J]. International journal of game theory, 1973, 2(1): 1-23. DOI: 10.1007/BF01737554.
[11] SELTEN R, STOECKER R. End behavior in sequences of finite Prisoner’s Dilemma supergames: A learning theory approach [J]. Journal of Economic Behavior & Organization, 1986, 7(1): 47-70. DOI: 10.1016/0167-2681(86)90021-1.
[12] YAO Wang, JIA Ning, ZHONG Shi-quan, LI Li-ying. Best response game of traffic on road network of non-signalized intersections [J]. Physica A: Statistical Mechanics and its Applications, 2018, 490: 386-401. DOI: 10.1016/j.physa. 2017.08.032.
[13] FAN Hong-qiang, JIA Bin, TIAN Jun-fang, YUN Li-fen. Characteristics of traffic flow at a non-signalized intersection in the framework of game theory [J]. Physica A: Statistical Mechanics and Its Applications, 2014, 415: 172-180. DOI: 10.1016/j.physa.2014.07.031.
[14] LIU Miao-miao, CHEN Yong-sheng, LU Guang-quan, WANG Yun-peng. Modeling crossing behavior of drivers at unsignalized intersections with consideration of risk perception [J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2017, 45: 14-26. DOI: 10.1016/j.trf.2016.11.012.
[15] BJORNSKAU T. The zebra crossing game–Using game theory to explain a discrepancy between road user behaviour and traffic rules [J]. Safety Science, 2017, 92: 298-301. DOI: 10.1016/j.ssci.2015.10.007.
[16] ALVAREZ I, POZNYAK A, MALO A. Urban traffic control problem: A game theory approach [C]// IEEE Decis Contr P. Seoul, Korea, 2008: 2168-2172. DOI: 10.3182/20080706-5- KR-1001. 01213.
[17] BUI K N, JUNG J J. Cooperative game-theoretic approach to traffic flow optimization for multiple intersections [J]. Computers & Electrical Engineering, 2017, 5: 1-13. DOI: 10.1016/j.compeleceng.2017.10.016.
[18] ELHENAWY M, ELBERY A A, HASSAN A A, RAKHA H A. An intersection game-theory-based traffic control algorithm in a connected vehicle environment [C]// 2015 IEEE 18th International Conference on Intelligent Transportation Systems. IEEE, 2015: 343-347. DOI: 10.1109/ITSC.2015.65.
[19] NAOHIRO U, EIICHI T. A study of dispatcher’s route choice model based on evolutionary game theory [J]. Procedia-Social and Behavioral Sciences, 2012, 39: 495-509. DOI: 10.1016/j.sbspro.2012.03.125.
[20] LIN Kai, LI Chen-si, GIANCARLO F, RODRIGUES J. Vehicle route selection based on game evolution in social internet of vehicles [J]. IEEE Internet of Things Journal, 2018, 5(4): 2423-2430. DOI: 10.1109/JIOT.2018.2844215.
[21] PORTILLA C, VALENCIA F. Non-linear model predictive control based on game theory for traffic control on highways [J]. IFAC Proceedings Volumes, 2012, 45(17): 436-441. DOI: 10.3182/20120823-5-NL-3013.00046.
[22] LIN Cheng, LOU Xiao-ming, ZHOU Jing, MA Jie. A mixed stochastic user equilibrium model considering influence of advanced traveler information systems in degradable transport network [J]. Journal of Central South University, 2018, 25(5): 1182-1194. DOI: 10.1007/s11771-018-3817-5.
[23] ADRIANO F, SIMONE G A. Mean field game approach for multi-lane traffic management [J]. IFAC Papersonline, 2018, 51(32): 793-798. DOI: 10.1016/j.ifacol.2018.11.448.
[24] YAN Fei, YAN Gao-wei, REN Mi-feng, TIAN Jian-yan, SHI Zhong-ke. A novel control strategy for balancing traffic flow in urban traffic network based on iterative learning control [J]. Physica A Statistical Mechanics & Its Applications, 2018, 508: 519-531. DOI: 10.1016/j.physa.2018.05.134.
[25] SU Bei-bei, CHANG Hong, CHEN Yong-zhou, HE Da-ren. A game theory model of urban public traffic networks [J]. Physica A: Statistical Mechanics and its Applications, 2007, 379(1): 291-297. DOI: 10.1016/j.physa.2006.12.049.
[26] CHANG Hui, XU Xiu-lian, HU Chin-kun, FU Chun-hua, FENG Ai-xia, HE Da-ren. A manipulator game model of urban public traffic network [J]. Physica A: Statistical Mechanics and Its Applications, 2014, 416: 378-385. DOI: 10.1016/j.physa.2014.09.015.
[27] SKRINJAR J P, ABRAMOVIC B, BRNJAC N. The use of game theory in urban transport planning [J]. Tehnicki Vjesnik-Technical Gazette, 2015, 22(6): 1617-1621. DOI: 10.17559/TV-20140108101820.
[28] OHTSUKI H, HAUERT C, LIEBERMAN E, NOWAK M A. A simple rule for the evolution of cooperation on graphs and social networks [J]. Nature, 2006, 441(7092): 502-505. DOI: 10.1038/nature04605.
[29] CHEN Xing-guang, ZHOU Jing, ZHU Zhen-tao. Evolutionary game analysis of the travel mode choice for urban travelers [J]. Journal of Industrial Engineering Engineering Management, 2009, 23(2): 130, 140-142. DOI:10.1109/CLEOE-EQEC.2009.5194697. (in Chinese)
[30] XIAO Hai-yan, DU Wei. Repeated games analysis of trip model choice behavior [J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(2): 24-28, 35. DOI: 10.16097/j.cnki.1009-6744.2015.02.004. (in Chinese)
[31] CALASTRI C, BORGHESI S, FAGIOLO G. How do people choose their commuting mode? An evolutionary approach to travel choices [J]. Economia Politica, 2018: 1-26. DOI: 10.1007/s40888-018-0099-1.
[32] CHEN Yue-xia, CHEN Long, ZHA Qi-fen. Carbon emissions measurement of urban traffic individual in Zhenjiang [J]. Journal of Jiangsu University: Natural Science Edition, 2015, 36(6): 645-649. DOI: 10.3969/j.issn.1671- 7775.2015.06.005. (in Chinese)
[33] CHATTERJEE K, VELNER Y. Hyperplane separation technique for multidimensional mean-payoff games [J]. Journal of Computer and System Sciences, 2017, 88: 500-515. DOI: 10.1016/j.jcss.2017.04.005.
(Edited by FANG Jing-hua)
中文导读
基于多维博弈的城市居民低碳出行演化趋势分析
摘要:在考虑低碳因素的城市居民出行过程中,出行者会通过观察其他人的出行方式,产生模仿、排斥等一系列活动,从而影响到后续的出行,由此过程可以看作出行群体成员之间的反复博弈。本文在对低碳背景下出行群体的这种博弈及其演化趋势分析的基础上,把交通方式的选择和是否接收低碳理念作为策略的两个维度,建立了居民低碳出行多维博弈模型,并结合演化博弈理论对不同城市居民的低碳出行选择进行仿真,得到选择的演化稳定策略,进而讨论了模型主要参数变化对演化过程及稳定策略的影响。结果表明,城市出行者将向着演化稳定策略的趋势发展。公共交通越发达的城市,接受低碳理念并选择低碳出行的比例越高。公共交通不够发达的城市可以通过鼓励个人慢行交通,加大对低碳出行的宣传等措施提高这个比例,但宣传等做法带来的积极效果较为有限。
关键词:低碳出行;演化;多维博弈;出行方式
Foundation item: Project(BK20160512) supported by the Natural Science Foundation of Jiangsu Province, China; Project(16YJCZH027) supported by the Humanity and Social Science Youth Foundation of Ministry of Education of China; Project(15GLC004) supported by the Social Science Foundation of Jiangsu Province, China
Received date: 2018-10-16; Accepted date: 2019-01-29
Corresponding author: WU Xiao-hui, PhD Candidate, Lecturer; Tel: +86-511-88797620; E-mail: wuxiaohui@ujs.edu.cn; ORCID: 0000-0001-8646-8517