分布式电源电网中电能质量调节装置优化配置
夏向阳1,龚芬1,杨珏1,张旻2,毛晓红2
(1.长沙理工大学 电气与信息工程学院,湖南 长沙,410077;
2.广州有色金属研究院,广东 广州,510651)
摘要:为了适应网络参数和谐波源的随机变化,提出一种改进的免疫-粒子群算法来优化配置电网中电能质量调节装置,并采用Matlab/Simulink仿真,验证其正确性和可行性。研究结果表明:该算法能在给定电网范围内统一优化配置滤波装置的安装地点及相应的参数, 减小系统损耗,将电压、功率因数等保持在规定的范围内,达到系统平均电压谐波总畸变率和投资成本最小的目的。
关键词:分布式发电;优化算法;谐波;电能质量调节装置;能量成本
中图分类号:TM727 文献标志码:A 文章编号:1672-7207(2011)10-3105-07
Optimal configuration of power quality conditioner in distributed generation network
XIA Xiang-yang1, GONG Fen1, YANG Jue1, ZHANG Min2, MAO Xiao-hong2
(1. College of Electrical Engineering, Changsha University of Science and Technology, Changsha 410077, China;
2. Guangzhou Research Institute of Non-ferrous Metals, Guangzhou 510651, China)
Abstract: In order to adapt the random change of network parameters and harmonic source, an improved immune-particle swarm optimization algorithm was proposed to configure well the power quality conditioner in distributed generation network. Matlab simulation was used to verify its correctness and feasibility. The results show that the algorithm can deploy optimally the filter’s installation location and other parameters in a given network, reduce the system loss, keep the voltage and power factor, etc. within specified range, and achieve the purpose of the least average total harmonic distortion of voltage and investment costs.
Key words: distributed generation; optimization algorithm; harmonic; power quality conditioner; energy cost
分布式发电(Distributed generation)[1-2]是通过规模不大、分布在负荷附近的发电设施进行经济、高效、可靠的发电,在现代城市供电中具有独有的环保和高效优势。但在含有风力发电或光伏发电的配电网中,由于其输出受天气影响较大,且具有随机变化特性,增大了系统电压波动;分布式电源通过逆变器接入电网,其开关器件的频繁开通和关断向电网注入了大量谐波和次谐波分量,导致电网电压和电流波形严重失真,影响着供、用电设备的安全、经济运行且造成了巨大的经济损失。为了使配电网中各节点谐波电压满足相应的谐波标准[3-4],在用户或电网中装设滤波装置是抑制谐波的一种有效措施。目前,国内外研究者对其进行了大量研究,如:贾贵玺等[5]提出在配电网中安装电压补偿设备,抑制各种陡然变化的电压波动;Kubota等[6]研究了分布式电源动态无功补偿控制策略;姚建红等[7-9]采用优化算法求最小代价在电网中配置滤波装置和研究分布式发电系统的无功优化问题。他们考虑注入网络的谐波和分布式发电的无功功率只按最严重情况或有限几种运行方式,或采用的优化算法本身具有局限性以及滤波装置只涉及有源或无源滤波器等。采用优化算法实现2种滤波装置的优化配置是目前工程应用的必然选择。在已有的优化设计方法中,有些假设条件较多,寻优空间较小,寻优能力不强,如进化算法(EP)、遗传算法(GA)等。本文在传统的免疫-粒子群算法中引入自适应惯性因子和正交交叉算子,前者通过自动调节可改变搜索能力,后者能使生成的初始群均匀地分布在解空间中,提高了种群多样性。通过建立统一优化配置的数学模型,采用C++编制的改进免疫-粒子群算法进行求解。Matlab/Simulink现场模拟仿真结果表明:该算法运行速度较快,较高精度地确定了滤波器的安装类型、安装位置和容量参数等,并取得了较好的滤波效果和经济效益。
1 含分布式电源电网中无功补偿和滤波装置优化配置的数学模型
由于分布式系统的并网建立在电力电子技术基础之上,非线性负载的增加会向电网注入大量的谐 波[10]。目前,消除谐波的方法主要有无源滤波器、有源滤波器和混合型滤波器。无源滤波器对最优安装位置选择时应考虑以下问题:(1) 避免接入电网时与电网阻抗发生谐振,引起电力系统的不稳定现象;(2) 尽可能获得无功功率最优化补偿;有源滤波器的容量及最优安装位置应该在满足谐波治理标准的前提下,注入电网的谐波电流尽可能小。总之,滤波装置的优化配置就是在保证网络各节点谐波电压含有率(HRU)和电压谐波总畸变率(THDU)在规定限值内,以及滤波装置安全可靠运行的前提下,使得电网平均电压谐波总畸变率和全网滤波装置的投资成本最小。
1.1 目标函数的建立
(1) 在装设滤波装置后,要使电网谐波含量在符合国家标准的基础上越小越好。本文以电网各母线平均电压谐波总畸变率为目标函数,即:
 (1)
(1)
式中:i为电网母线标号;N为网络总节点数;h为谐波次数;H为考虑的最高谐波次数;U1i为第i点基波电压有效值;Uhi为第i点h次谐波电压有效值。在求解过程中,加入约束条件:
 (2)
(2)
Uhi≤Uhmax (3)
(2) 通过比较计算可以得到无功功率注入对系统有功损耗影响较大的那些节点,并把它们作为无源滤波器的预装位置,这样,就可以在不影响优化质量的条件下大大缩小算法的搜索空间,从而节省计算量和计算时间。为此,定义系统有功网损目标函数[9]如下:
min f2=Ploss (4)
分布式电源主要向电网输送有功功率,当无功功率取得过大时,并网逆变器的容量就会变得很大,从经济角度综合考虑,无功功率容量应有一定限制。此时,选取分布式电源提供的无功补偿容量Qgi为控制变量,电网各负荷节点的电压幅值Ui为状态变量,它们需要满足:
Qgimin≤Qgi≤Qgimax (5)
Uimin≤Ui≤Uimax (6)
其中:Ploss为系统有功网损;Qgimax和Qgimin分别为节点i处得无功补偿容量上、下限值;Uimin和Uimax分别为电压上、下限值。
(3) 通过采用无源滤波器和有源滤波器的数学模型,得到投资费用最小的目标函数f3(x)为:
 (7)
(7)
式中:M为每个节点所能安装的滤波装置支路个数;aij和bi表示是否安装滤波器支路,aij=1,表示第i节点安装第j条无源滤波器支路,bi=1,表示第i节点安装有源滤波器支路;fPij(QCNij)为电容器的费用与其额定容量之间的函数关系;fAi(Si)为有源滤波器费用与其额定容量之间的函数关系。
滤波装置的无功补偿性能主要包括2个方面:基波无功功率的补偿和谐波无功功率的补偿。而非线性负载的功率因数对系统滤波装置优化配置的影响主要表现在滤波装置的最小额定安装容量上,根据文献[11]可知:
 (8)
(8)
其中: ;Q1为补偿的基波无功容量;
;Q1为补偿的基波无功容量;
Qhi为补偿的谐波无功容量;I1i和Ihi为第i节点的基波电流和第h次谐波电流;Ci为第i节点安装滤波器的电容。另外,根据无源滤波器的滤波原理中电感L、电阻R与电容C的关系,进而可求出L和R。
有源滤波器的容量Si由所补偿的各次谐波电流决定,而与基波电流无关,其容量决定于所补偿的总谐波电流有效值,即:
 (9)
(9)
约束条件为:
 (10)
(10)
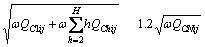 (11)
(11)
 (12)
(12)
Si≤SNi (13)
在实际情况中,要使3个目标函数同时到达最小是不可能的,而只能通过协调各函数之间的关系,尽量使它们同时达到比较优的解。因此,本文采用线性加权的方式给出综合目标函数,使多目标优化问题转化为单目标优化问题。
1.2 适应值计算
罚函数法[11]的基本思想是根据约束的特点构造某种惩罚函数,并将惩罚函数添加到目标函数中,使约束优化问题的求解转化为无约束优化问题的求解。本文在目标函数中引入罚函数来计算适应值,即
 (14)
(14)
式中:V为一适当大的正整数;ri和cj为罚因子。在实际计算中,它们的取值很难确定,若太小则起不到惩罚作用,若太大则由于误差的影响会导致错误。本文在计算过程中先将其取较小的正数,求出F(x)最优解;当这个解不满足有约束最优化问题的约束条件时,放大惩罚因子重复进行,直到满足条件为止。Gi和Hj分别是约束条件gi和hj的函数:
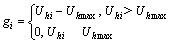 (15)
(15)
 (16)
(16)
 (17)
(17)
2 改进的免疫-粒子群算法
2.1 正交交叉算子
人工免疫系统是模仿生物免疫系统的免疫应答、免疫记忆、免疫调节等机理,构造出一类高性能、自组织、鲁棒性好的人工智能系统[12]。随着人工免疫系统研究的深入,产生了不少模型和算法。首先得到认可的是克隆选择算法,但它要求只有亲和度高、结合能力强的抗体才可以保留下来,所以,容易造成陷入局部最优,且收敛速度慢。为此,在免疫算法中引入正交交叉算子,初始化种群,使其均匀化,随机生成新个体,维持种群多样性。
设2个父代个体x1={x1,1,…,x1,N},x2={x2,1,…,x2,N},m={min(x1,1,x2,1),…,min(x1,N,x2,N)},n={max(x1,1,x2,1),…,min(x1,N,x2,N)},将空间{m,n}的每一个区域量化,使得相邻2个水平的差是相同的,再利用正交表选择出较小数且具有代表性的个体作为子代个体,加入到群体中。
2.2 自适应惯性系数
PSO算法[13-15]是一种基于群集智能的具有全局寻优能力的优化工具,其目标就是全局最优解。在PSO算法中,假设粒子的总数为N,每个粒子在空间中有一个位置xi,该粒子从xi以速度vi向前飞行,每个粒子在空间内搜索到的最优位置为pi,整个粒子群在空间内搜索到的最优位置为pg,xi的第k次迭代的修正量为 ,则:
,则:

 ,i=1,2,…,N (18)
,i=1,2,…,N (18)
式中:k为迭代次数;c1和c2为加速因子;r1和r2为2个独立的介于[0,1]之间的随机数;w为惯性系数,调整其值可以改变搜索能力。算法的迭代终止条件为:当最大迭代次数或粒子群迄今为止搜索到的最优位置的适应度满足预定的最小适应度阈值时算法终止。
虽然它操作简单,使用方便且收敛速度较快,但由于粒子都是根据全体粒子和自身的搜索经验向着最优解的方向“飞行”,可能会缺乏对最优解的精细搜索而导致搜索精度不高。为此,本文采用自适应惯性系数,按式(19)对w进行自适应调整,即随着迭代次数的增加,逐步减少w。w较大有利于提高算法的收敛速度,而w较小则可以提高算法的精度。
 (19)
(19)
式中:k为迭代次数;kmax为迭代次数的上限。
为了加快收敛速度,同时保持粒子群的多样性,本文提出了改进的免疫-粒子群优化算法,即将粒子群进化方程中引入含正交交叉算子的免疫克隆算法,这样,每个抗体利用已有的历史信息飞向全局最优解。改进后的算法大大减少了运行时间,提高了算法精度,从而准确确定装置的安装位置、类型及容量,减小系统有功损耗,将电压、功率因数等保持在规定的范围内,并使装置的购买费用及安装投资费用与电网的网损费用之和最小。
3 求解算法
3.1 算法流程图
通过以上分析,采用改进免疫-粒子算法对含分布式发电的电网中滤波器进行优化配置,从而可以得到算法流程图如图1所示。
3.2 算例分析
采用12节点含分布式电源的三相平衡电力网络,其结构见图2。系统基准容量为10 MV·A,除节点1外,所有节点电压均为10 kV。节点4,5,6,7,8,9,11和12处有谐波源,其中节点4,7和12处为确定性谐波源(如节点4和12处的分布式电源通过逆变器接入电网,其开关器件频繁的开通和关断向电网注入了大量的谐波),节点5和8以及6和9处为2组不同时段工作的非确定性谐波源,这样就可把系统多谐波源负荷动态运行分成2组静态多谐波源负荷运行综合考虑。

图1 算法流程图
Fig.1 Algorithm flow chart

图2 网络结构图
Fig.2 Network structure
利用上述模型及求解方法,采用C++编程对所给配电网络进行计算,算法参数选为群体规模N=60,c1=c2=1.0,kmax=50,独立运行20次[16]。由于自适应的惯性系数和正交交叉算子的引入,在保证较高的搜索精度时也大大加快了算法的收敛速度。寻优计算结果表明谐波源对节点4,6,8,9和12的影响较大。为了避开容易谐振的频率点,保证各节点电压总畸变率满足限值要求,同时在最优的经济条件下,分别在节点6和9处投入无源滤波器,在节点4投入有源滤波器,取得最优配置结果如表1所示(其中,C,L,R和Q为优化方案中的无源滤波器的电容、电感、电阻及品质因数)。
表1 无源滤波器参数配置
Table 1 Parameters configuration of PPF

为了更进一步证实该算法的优越性,分别采用粒子群算法和模拟退火-粒子群算法对算例进行寻优计算,所得结果如表2所示。
在没有安装滤波装置之前,系统中的谐波电压以5,7,9,11和13次谐波的为主,各节点的平均电压谐波总畸变为7.67%,最大为12.55%,位于节点9。通过采用改进的优化算法进行优化配置,得到各谐波源节点 和总
和总 如表3所示。
如表3所示。
表2 不同寻优算法的结果比较
Table 2 Comparison of different optimization algorithms

表3 投入滤波装置前后各节点的 和
和
Table 3 HRU and THDU before and after inputting filter devices

由表3可知:在适当的节点安装滤波装置后,系统各次谐波含量明显提高,满足谐波标准。同时,本文方法明显优于传统的设计方法,它实现了对所有高次和低次谐波的有效抑制,并提供了一定无功功率,系统功率因数也得到提高。然而,为了使无源滤波器在电网频率变化或者本身参数有一定制造误差时仍有较好的滤波效果,并有效避免串、并联谐振,在设计过程中应将其谐振频率设置比谐波特征谐波频率低。以上结果充分说明了本文所提出的滤波器优化配置方法的有效性。
4 仿真结果及分析
为了更好地检测系统的滤波效果,建立模拟实验模型。本实验主要从节点2处检测电网电流波形,从而验证算法的优越性及滤波装置的滤波特性。
取系统采样频率为6.4 kHz,电源相电压为220 V(50 Hz时);系统阻抗为0.1 Ω,电感为0.05 mH。谐波源是模拟特征谐波分量的电流源,基波电流为80 A,3次谐波电流为8 A,5次谐波电流为5 A,7次谐波电流为3 A,11次谐波电流为2 A,各次谐波电流的初相角为0°,滤波装置参数见表3,从而得到滤波装置投入前、后的稳态电网侧电流波形分别如图3~6所示。
由图3~6可知:采用改进免疫-粒子群算法在最优安装点投入有源和无源滤波器后,电网侧电流波形由畸变波形被改善为接近正弦波,电流中的谐波和无功分量大大减少,且效果明显优于PSO算法和SA-PSO算法。由此可见,改进的优化算法中,粒子群算法采用随迭代次数w逐步减小,能灵活地调整粒子在全局和局部搜索能力之间的平衡,保证了初期收敛速度较高和后期收敛精度较高;而免疫算法中正交交叉算子维持了种群的多样性,提高了算法的精度并没有影响到算法的运行时间,从而达到了全网滤波装置投资最少的目的。

图3 滤波器投入前电网侧电流波形
Fig.3 Grid side current waveform before filter input
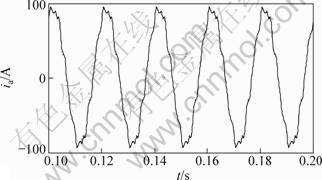
图4 基于PSO配置滤波装置后电网侧电流波形
Fig.4 Grid side current waveform after configuring filter devices based on PSO

图5 基于SA-PSO配置滤波装置后电网侧电流波形
Fig.5 Grid side current waveform after configuring filter devices based on SA-PSO

图6 基于IIA-PSO配置滤波装置后电网侧电流波形
Fig.6 Grid side current waveform after configuring filter devices based on IIA-PSO
5 结论
(1) 改进的免疫-粒子群算法能以更大概率、更快速度获得全局最优解。
(2) 在对分布式发电的电网滤波装置进行优化配置时,由于无源滤波器主要是滤除较低次数的谐波和补偿无功功率,而有源滤波器则负责滤除较高次数的谐波,这样大大减小了所需变流器的容量,从而达到了较好的滤波效果和经济效益,特别适合于实际工程应用。
(3) 在算法流程中,部分参数的载入是由抗体当前最佳亲和度与目标值进行自适应调整的,更灵活的调整方案有待进一步研究。
参考文献:
[1] 梁才浩, 段献忠. 分布式发电及其对电力系统的影响[J]. 电力系统自动化, 2001, 25(12): 53-56.
LIANG Cai-hao, DUAN Xian-zhong. Distributed generation and its impact on power system[J]. Automation of Electric Power Systems, 2001, 25(12): 53-56.
[2] 王建, 李兴源, 邱晓燕. 含有分布式发电装置的电力系统研究综述[J]. 电力系统自动化, 2005, 29(24): 90-97.
WANG Jian, LI Xing-yuan, QIU Xiao-yan. Power system research on distributed generation penetration[J]. Automation of Electric Power Systems, 2005, 29(24): 90-97.
[3] 吴竞吕. 供电系统谐波[M]. 北京: 中国电力出版社, 1998: 24-27.
WU Jing-lü. Power supply system harmonics[M]. Beijing: China Electric Power Press, 1998: 24-27.
[4] GB/T 14549—93, 电能质量: 公用电网谐波[S].
GB/T 14549—93, Quality of electric energy supply harmonics in public supply network[S].
[5] 贾贵玺, 戚艳, 傅田晟, 等. 分布式电源动态无功补偿控制策略[J]. 电力系统及其自动化学报, 2009, 21(1): 27-31.
JIA Gui-xi, QI Yan, FU Tian-sheng, et al. Control strategy of dynamic reactive compensation of distributed generation[J]. Proceedings of the Chinese Society of University for Electric Power System and its Automation, 2009, 21(1): 27-31.
[6] Kubota Y, Genji T, Miyazato K, et a1. Verification of cooperative control method for voltage control equipment on distribution network simulator considering interconnection of wind power generators[C]//IEEE/PES Trans and Distribution Conference, Yokohama, Japan: 2002: 112-116.
[7] 姚建红, 刘继承. 微粒子群算法在有源电力滤波器优化配置中的应用[J]. 化工自动化及仪表, 2009, 36(1): 35-38.
YAO Jian-hong, LIU Ji-cheng. Particle swarm optimization applied in optimization configuration of active power filter[J]. Control and Instruments in Chemical Industry, 2009, 36(1): 35-38.
[8] 赵勇, 邓红英, 李建华, 等. 基于机会约束规划的配电网滤波装置优化配置[J]. 中国电机工程学报, 2001, 21(1): 12-17.
ZHAO Yong, DENG Hong-ying, LI Jian-hua, et al. Chance constrained programming based optimal allocation of harmonic filters on a distribution network[J]. Proceedings of the CSEE, 2001, 21(1): 12-17.
[9] 王瑞, 林飞, 游小杰, 等. 基于遗传算法的分布式发电系统无功优化控制策略研究[J]. 电力系统保护与控制, 2009, 37(2): 24-28.
WANG Rui, LIN Fei, YOU Xiao-jie, et al. Research on the reactive power control of distributed generation system based on genetic algorithm[J]. Power System Protection and Control, 2009, 37(2): 24-28.
[10] 梁有伟, 胡志坚, 陈允平. 分布式发电及其在电力系统中的应用研究综述[J]. 电网技术, 2003, 27(12): 72-77.
LIANG You-wei, HU Zhi-jian, CHEN Yun-ping. A survey of distributed generation and its application in power system[J]. Power System Technology, 2003, 27(12): 72-77.
[11] 沈红, 赵勇, 李建华, 等. 考虑谐波源随机过程的配电网络滤波装置优化配置[J]. 电网技术, 2002, 26(11): 15-19.
SHENG Hong, ZHAO Yong, LI Jian-hua, et al. Optimal configuration of harmonic filters in distribution networks considering stochastic process of harmonic sources[J]. Power System Technology, 2002, 26(11): 15-19.
[12] 罗一丹, 蔡自兴, 龚涛, 等. 一种新的免疫进化算法在函数优化中的应用[J]. 计算机工程与科学, 2008, 30(8): 49-52.
LUO Yi-dan, CAI Zi-xing, GONG Tao, et al. A new immune evolution algorithm and its application in function optimization[J]. Computer Engineering and Sicence, 2008, 30(8): 49-52.
[13] Boeringer D W, Werner D H.A comparison of particle swarm optimization and genetic algorithms for a phased array synthesis problem[C]//Antennas and Propagation Society International Symposium. United States, 2003: 181-184.
[14] 唐剑东, 熊心银, 吴耀武, 等. 基于改进PSO算法的电力系统无功优化[J]. 电力自动化设备, 2004, 24(7): 81-84.
TANG Jian-dong, XIONG Xin-yin, WU Yao-wu, et al. Power system reactive power optimization based on modified particle swarm optimization algorithm[J]. Electric Power Automation Equipment, 2004, 24(7): 81-84.
[15] 何娜, 黄丽娜, 武健, 等. 基于粒子群优化算法的混合有源滤波器中无源滤波器的多目标优化设计[J]. 中国电机工程学报, 2008, 28(27): 63-69.
HE Na, HUANG Li-na, WU Jian, et al. Multi-objective optimal design for passive part of hybrid active power filter based on particle swarm optimization[J]. Proceedings of the CSEE, 2008, 28(27): 63-69.
[16] 张俊芳, 姚强, 杭银丽. 含分布式电源的配电网谐波潮流计算[J]. 电力科学与技术学报, 2011, 26(2): 89-93.
ZHANG Jun-fang, Yao Qiang, HANG Yin-li. Harmonics power flow calculation of distribution networks with DG[J]. Journal of Electric Power Science and Technology, 2011, 26(2): 89-93.
(编辑 陈灿华)
收稿日期:2011-04-29;修回日期:2011-07-03
基金项目:广东省科技计划重大专项(2010A080804023);湖南省自然科学基金资助项目(1011JJ5027);长沙市科技计划项目(K1104024)
通信作者:夏向阳(1968-),男,湖南长沙人,副教授,从事电力系统自动化和电能质量控制等研究;电话:13873191528;E-mail:xia_xy@126.com