文章编号：1004-0609(2015)-11-2953-09

镍基高温合金相关相图的高通量测定与热力学优化

朱礼龙¹，戚海英²，江  亮¹，金展鹏³

(1. 中南大学 粉末冶金国家重点实验室，长沙 410083；

2. 深圳市万泽中南研究院有限公司，深圳 518017；

3. 中南大学 材料科学与工程学院，长沙 410083)

摘  要：对相图的常用实验测定方法进行综述，以Cr-Ni-Ru三元体系相图的高通量测定为例，展示高效测定二元、三元相图的扩散多元节方法。基于相图计算(Calculation of phase diagrams, CALPHAD)方法，以 Cr-Ru二元体系和Cr-Ni-Ru三元体系的热力学优化为例，阐述Cr-Ni-Ru三元体系热力学数据库建立的具体流程，分析当前镍基高温合金研究效率低下的原因。结果表明：快速建立与定量预测材料成分、相、组织、性能关系的高通量实验和计算方法是促进未来镍基高温合金研究发展的重点。

关键词：镍基高温合金；扩散多元节；高通量方法； CALPHAD方法；相图；热力学优化

中图分类号：TG113.14　　     文献标志码：A

High-throughput experimental determination and thermodynamic assessment of phase diagrams of nickel-based superalloys

ZHU Li-long¹, QI Hai-ying², JIANG Liang¹, JIN Zhan-peng³

(1. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;

2. Shenzhen Wedge Central South Research Institute Co., Ltd., Shenzhen 518017, China;

3. School of Materials Science and Engineering, Central South University, Changsha 410083, China)

Abstract: The experimental methods for phase diagram determination were reviewed. Comparing with the traditional methods for phase diagram determination, the Cr-Ni-Ru ternary system was employed to illustrate the high efficiency and accuracy of the diffusion multiple technique in the binary and ternary phase diagrams determination. Based on the calculation of phase diagrams (CALPHAD) approach, thermodynamic assessments were performed in the Cr-Ru and Cr-Ni-Ru systems to expound the procedure of the establishment of the Cr-Ni-Ru thermodynamic database. The reasons resulting in the inefficiency of the development of nickel-based superalloys were also discussed. The results show that high-throughput experimental and computational methods for efficiently predicting and establishing the relationships among composition, phase, microstructure and property are fundamental importance for promoting the development of nickel-based super alloys.

Key words: nickel-based superalloy; diffusion multiple; high-throughput method; CALPHAD method; phase diagram; thermodynamic assessment

镍基高温合金具有优异的高温强度、蠕变、疲劳性能及抗氧化、抗腐蚀等性能，并且在高温条件下具有良好的组织稳定性和使用可靠性，因此被广泛地应用于航空发动机和各种工业燃气轮机^[1]。通常，镍基高温合金由10种以上的合金元素组成，面心立方结构的Ni是基体元素，具有较好的塑性变形能力及高温稳定性，其他合金元素的添加主要通过固溶强化、析出相强化、晶界强化等强化作用来提高镍基高温合金的高温性能^[2]。

随着航空航天技术的不断发展，提高发动机的推力和燃油效率一直是科学家与工程师一致追求的目标，而实现这一目标最为主要的实现方式是提高发动机涡轮的入口温度^[3]。很显然，涡轮入口温度的提高必然需要开发具有更高承温、承载能力的高温合金材料。当前，先进的镍基高温合金在使用过程中，其承受的平均温度为1050 ℃，有时甚至高达1200 ℃(接近其熔化温度的85%~90%)^[4]。因此，在高温合金的设计过程中，一个重要的思路就是添加大量的Ta、Mo、W、Re和Ru等高熔点金属元素来提高合金的固相线温度，进而提高合金的承温能力。同时，这些难熔金属元素在高温合金中起到了很好的固溶强化效果，极大地提高了合金的高温强度与蠕变等性能^[5-6]。然而，有研究表明^[7-9]，含过高浓度难熔金属的镍基高温合金，长时间在高温、高应力等复杂环境服役的过程中会形成大量有害的拓扑密排相(Topologically closed packed phase，TCP相)，从而严重地降低合金的高温蠕变与抗氧化腐蚀性能。

假如高温合金的设计研发仍然仅仅依靠长期积累的经验和凭借科研人员的专业知识与能力，采用传统的耗时费力的试错法(Trial and error)来完成，将不能摆脱一种新材料从初始研发到最终应用通常需要耗费 10~20 年^[10]的困境。材料科学工作者在试错的过程中积累了大量宝贵的经验，也涌现了不少成功的研发案例，但在很大程度上仍具有一定的偶然性和局限性，并不能形成一种材料设计研发的“范例”来推广到更加广泛的领域。对于镍基高温合金来说，其合金成分及制造工艺过程都极其复杂，其研制周期也相对较长。以只针对优化镍基高温合金的一种使役性能，并且仅对其7个主要合金元素的成分进行设计及优化为例，假设每种主要合金元素的最优含量的范围在 0~10%(质量分数)，采用传统试错法的方法，以每种合金元素的 1%(质量分数)为增量水平来设计试验，那么就需要制备多达1×10⁷ 个合金进行检测与分析^[11]。这个实验过程的工作量非常大，显然超出了任何科研项目的能力和时间限制。

相图反映某种材料体系在一定的温度、压力、组成成分等条件下的相组成及相变信息^[12]，是合金设计中成分、相、组织、性能关系的基础。相图的建立通常有两种方法：实验测定和热力学计算。20世纪 60 年代之前，获得相图的主要手段是通过大量而繁琐的实验来测定，往往非常耗时费力且实验成本高昂。而所测定的相图多局限于一些简单的二元系以及三元系的有限的成分区域，几乎不可能获得成分范围广的多组元体系相图。然而，在很多的合金体系中，特别是镍基高温合金，往往需要添加多种合金元素以提高其综合性能指标。因此，多组元合金相图对合金的设计往往更具有指导意义。

随着计算材料科学的发展，相图计算 (Calculation of phase diagrams, CALPHAD)方法^[13]逐渐成熟，已发展成为材料科学的重要分支和材料设计的有力工具，因而广泛地应用于科学研究和工程领域。CALPHAD的核心是用实验结果(主要是二元相图和三元平衡相关系或相图再加上相关相的形成焓、混合焓、比热、活度等)拟合/优化出各相在整个成分范围与从室温到超高温度范围内其吉布斯自由能随成分、温度和压力变化的关系式，并据此形成热力学数据库。CALPHAD 与多元合金热力学数据库相结合，可以实现多元合金中各相的相分数、相成分和点阵分数的热力学计算，从而指导合金成分设计及工艺优化。 CALPHAD 方法在高温合金的研究中发挥着重要作用，相计算(Phase computation, PHACOMP)的出现最初就是用于解决镍基高温合金的实际生产问题^[14]。美国国家研究理事会(NRC)2012 年发表的报告《轻质化技术在军用飞机、舰船和车辆中的应用》中引用了两个成功的集成材料计算(Integrated computational materials engineering, ICME)与实验的合金设计实例^[15]，其中一个就是通用电气公司(GE)开发的燃气轮机用 GTD262 高温合金^[16]。该合金从最初设计到实际生产应用只用了4年时间，并大幅降低了开发成本。

虽然，当前的镍基高温合金热力学数据库已经比较成熟，可以对合金体系中的基体-γ相和最主要强化相-γ′相的热力学稳定性进行很好的预测，但是对TCP相的预测能力则非常有限^{[14, 17]}。因此，仍需要大量的实验测定与热力学优化工作，来进一步完善镍基高温合金热力学数据库，扩展数据库中所包含的元素，进而提高对TCP相的预测精度与可靠性。针对镍基高温合金中TCP相相关的Cr-Ni-Ru 三元体系，本文作者阐述了扩散多元节的制备流程以及从扩散多元节中快速高通量地获得Cr-Ni-Ru三元系相图等温截面的方法。并且阐述了热力学优化的基本流程，获得了优化的Cr-Ni-Ru三元体系热力学参数，并且将计算的Cr-Ni-Ru三元体系相平衡结果与实验和文献中的数据进行了比较。

1  相图的实验测定方法

常用的相图测定方法主要有平衡合金法和扩散偶法以及近期发展的扩散多元节方法^[18]。平衡合金法对每一个合金试样的表征分析，可以获得临近合金成分的相平衡关系。扩散偶法对每一个扩散偶的表征分析可以获得扩散偶成分范围内的相平衡关系。区别于平衡合金法和扩散偶法需要制备多个试样的特点，扩散多元节方法可以在一个试样上实现比前两者更大成分范围内的相平衡关系，是一种高通量的合金制备和相图测定方法。

1.1  平衡合金法(Equilibrated alloy)

平衡合金法是一种传统的并被广泛采用的相图测定方法。合金法的一般做法是：通过真空熔炼或粉末冶金方法来制备选定成分(Nominal composition)的合金；将获得的合金在低于固相线温度的某一较高温度下进行均匀化退火，消除合金凝固偏析或粉末原始颗粒的成分不均匀；再将均匀化退火之后的合金在某些温度下进行长时间的扩散退火，形成包含相应退火温度下相平衡关系的微观组织；最后，结合X射线衍射(XRD)、光学显微镜(OM)、扫描电镜(SEM)、电子探针微区分析(EPMA)等分析检测设备来获取该温度下的平衡相的结构、成分等信息，进而建立所测体系的相平衡关系。

EPMA是目前测定各相平衡成分的最有效工具，对于一个三元系相图而言，从EPMA测定结果中可提取出绘制该体系相图等温截面所需要的结线(Tie-line)和三相区结三角(Tie-triangle)信息。对于每一个配制的合金，如果该合金的名义成分位于两相区或三相区，可以获得一条结线或一个三相区结三角；如果该合金的成分位于单相区，则不能获得任何结线。而精确测定三元系相图的一个等温截面，通常需要很多条结线与三相区结线，因此需要配制大量的合金样品。如图1(a)所示，SHAO等^[19]制备了100多个合金来测定Al-Cr-Ti三元系1000 ℃等温截面。

为了保证所测得的数据的可靠性，合金法测定相图要求合金在退火后必须达到热力学平衡状态，即随着退火时间的延长，各相的化学成分不再发生改变。一般而言，金属元素在低温下的原子移动速率小，因此在测定较低温度(600~900 ℃)的等温截面时，往往需要很长的退火时间。对于一些含难熔金属元素，如Ta、Mo、W、Re和Ru等的三元体系，在合金凝固的过程中容易形成严重的成分偏析，即使经过长时间的退火处理也很难消除。平衡合金法作为一种重要的相图测定方法，但是其效率非常低，难以满足在短期内完善镍基高温合金实验相图数据库的迫切需求。

1.2  扩散偶法(Diffusion couple)

扩散偶法最初主要是用于研究多相扩散、固态焊接以及界面反应等问题，后经HASEBE^[20]和金展鹏 等^[21-23]的创新与改进，使其成为一种测定金属固态相关系的一种常用、高效的方法。扩散偶法用于相图测定是基于局部平衡(Local phase equilibrium)^[24-26]的假设之上，即在一定的温度和压力下，一个体系在整体上没有达到自由能最小状态，但在扩散层界面附近的局部区域却出现了自由能为最小值的状态(相应元素在界面两端各相中的化学势相等)，因而可以认为在这个局部处于平衡状态。

扩散偶的基本制备流程是将两种或多种固态块体材料的表面经打磨、抛光、清洗等处理后，在外力的作用下形成紧密的界面接触。然后在设定温度下通过原子间的相互扩散而形成具有一定厚度的扩散层，即形成在一定成分范围内具有连续成分变化的固溶体和化合物相，从而可以在一个试样中获得具有微观分辨率的成千上万种合金成分。最后结合SEM、EPMA等分析检测工具，可获得大量绘制相图所需要的结线及三相区结线等信息，进而实现相图的快速测定。

1.3  扩散多元节方法(Diffusion multiple)

扩散多元节方法^[27-31]更新发展了传统的扩散偶技术。扩散多元节是将多个块状金属以预定的方式排列，形成多个二元扩散偶和三元扩散节点的方法，因而比传统扩散偶法具有更高的效率。扩散多元节中的三元节点可以用来非常快速地测定三元相图等温截面，为建立多组元热力学数据库提供可靠的实验数据。图1(a)所示为SHAO等^[19]从100多个平衡合金中获得的Al-Cr-Ti 体系1000 ℃的等温截面；图1(b)所示为扩散多元节横截面示意图；图1(c)所示为通过 Ti-Cr-TiAl₃-TiSi₂ 扩散多元节方法测定的Al-Cr-Ti 三元系在 1000 ℃的等温截面。将其和通过 100 多个平衡合金所测得的Al-Cr-Ti 三元系在 1000 ℃的等温截面(见图1(a))相比，可以看出两种方法所测得的相图一致性非常好。通过在多个合金体系的实践，采用扩散多元节方法高通量测定三元系相图展示了很好的可靠性^[32-33]。

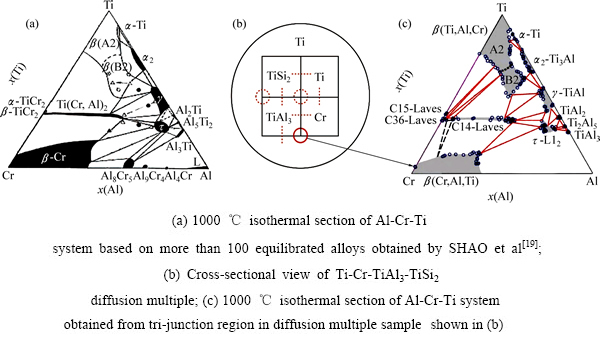
图1  利用扩散多元节研究钛合金体系相图

Fig. 1  Application of diffusion-multiple approach to study of Ti-base phase diagrams

2  Cr-Ni-Ru三元系相图的高通量测定

2.1  Cr-Ni-Ru三元系相图的研究现状

含高浓度难熔金属Ta、Mo、W和Re等的镍基高温合金，在服役的过程中可能会形成大量有害的TCP相，进而严重降低了合金的高温性能。有研究发     现^[34-38]，少量Ru的添加可以极大地提高合金的组织稳定性，抑制TCP相的形成，这也使得Ru元素成为第四代单晶高温合金的标志性元素。在镍基高温合金中，Al和Cr是极其重要的合金元素，Al和Cr可以提高合金的高温抗氧化能力，而且Al也是强化相γ′相的重要组成元素。为了理解Ru元素在多元镍基高温合金中的作用机理，Ni-Al-Cr-Ru四元体系相图，特别是Al-Ni-Ru和Cr-Ni-Ru三元系是非常重要的。目前，Al-Ni-Ru三元体系相图的研究已非常系统^[39-46]，但Cr-Ni-Ru三元系却只有很少的实验数据。CHAKRAVORTY等^[47]和ZHU^[48]分别采用具有不同成分的2个合金和4个合金来测定Cr-Ni-Ru三元体系的相图等温截面，因此，他们的测定结果仅包含非常有限的成分范围，而且没有精确地确定各相区(FCC(Ni)、BCC(Cr)、HCP(Ru)与σ相)的相边界。

σ相是一种常见的TCP相，σ相的析出对高温合金的性能有显著的不良影响，是高温合金设计中需要规避的显微组织。因此，精确测定Cr-Ni-Ru体系中σ相的相边界与稳定存在的成分范围对于理解含Ru镍基高温合金中σ相的形成机理具有重要的指导意义。同时，完善的Cr-Ni-Ru三元系实验数据，可以用于该三元体系的热力学优化，获得描述各相的吉布斯自由能表达式中的各个参数，进而建立可靠的Cr-Ni-Ru三元系热力学数据库。

2.2  Cr-Ni-Ru-NiAl-RuAl扩散多元节的设计与制备

ZHU等^[49]通过制备Cr-Ni-Ru-NiAl-RuAl扩散多元节，系统地测定了Cr-Ni-Ru三元系相图在1200、1000、900和800 ℃的等温截面。Cr-Ni-Ru-NiAl-RuAl扩散多元节的制备流程如图2所示，其中，图2(a)和2(b)所示分别为扩散多元节的横截面和纵截面示意图。最外层的Ni和次外层的Cr均作为扩散多元节的包套，其内部分别用Ni、Ru、NiAl和RuAl填充。高纯原材料Ni(99.98%，质量分数)、Cr(99.95%)、Ru(99.95%)及合金NiAl、RuAl按图2(a)和2(b)所示的尺寸进行线切割。切割后的试样经打磨、抛光、超声波清洗后，按图纸进行组装。然后采用真空电子束焊接(Electro-beam welding, EB-welding)在组装后的试样的上下两端分别焊接一个厚度为5 mm的盖子。这样就可以在扩散多元节内部形成了一个完全密封的真空环境，接下来将扩散多元节试样进行热等静压(Hot isostatic pressing, HIP)处理。HIP在200 MPa的氩气环境中和1200 ℃温度下进行，保持4 h。在1200 ℃温度下，200 MPa的等静压力可以使扩散多元节发生形变，进而促进其内部形成非常紧密的界面接触。同时保温4 h，相互接触的界面间会发生剧烈的原子互扩散现象，形成相应的扩散层，从而又进一步促进了界面间的接合。经过以上步骤，就成功地制备了一个Cr-Ni-Ru-NiAl-RuAl扩散多元节。然后，将该扩散多元节沿着试样高度方向，平均切割成4片(每片厚度约为6 mm)，分别放在1200、1000、900和800 ℃下进行700、1040、1050和1050 h的退火处理。为了避免扩散多元节试样在高温退火过程中发生氧化，影响所测定相图的准确性，在退火前需要将每片扩散多元节试样分别真空(约为1×10^-3 Pa)密封在石英管中。并且将小块的钇用高纯钽箔包裹，和试样一起密封在石英管中，以吸收石英管中残留的氧或在退火过程中扩散到石英管中的氧。退火结束后，将试样快速水淬至室温，避免试样因冷却时间过长而发生相变，以保存在相应设定温度下的相平衡关系。

图2  Cr-Ni-Ru-NiAl-RuAl扩散多元节的组装与制备

Fig. 2  Assembly and fabrication of Cr-Ni-Ru-NiAl-RuAl diffusion

2.3  Cr-Ni-Ru三元系相图的测定

结合OM、SEM、EPMA等分析检测技术，可以快速完成Cr-Ni-Ru三元系相图等温截面的测定。图3(a)所示为Cr-Ni-Ru-NiAl-RuAl扩散多元节试样中Cr-Ni-Ru三元体系在1000 ℃退火1040 h后的SEM背散射电子像，显示了Ni、Cr和Ru元素在1000 ℃下相互扩散而形成的显微组织。图3(b)为根据图3(a)所绘制的示意图，从图3(b)中可更加清晰地看出各扩散层所对应的相平衡关系，即在1000 ℃相图等温截面 中存在着4个两相平衡(FCC(Ni)-BCC(Cr)、FCC(Ni)-HCP(Ru)、BCC(Cr)-σ)和HCP(Ru)-σ)与2个三相平衡(FCC(Ni)-BCC(Cr)-σ和FCC(Ni)-HCP(Ru)- σ)。虽然BCC(Cr)这一相层中也存在明显的衬度差，但其实这并不是一个相界面，而是由于Cr元素在这个“界面”附近有很大的浓度梯度而引起的。EPMA成分检测在扩散层中相界面附近进行，测试时沿着大致垂直相界面的方向进行打点。根据扩散层厚度的不同，将打点的步长设置为1或2 μm，每条线扫描由20个左右的点组成。通过获得的EPMA测试结果，可以绘制成分-距离曲线，以及包含这些数据点的相图等温截面，结合这两种图形，就可以提取出一条结线。从获得的EPMA成分曲线中提取结线数据的具体方法在文献[18, 49]中已有详细地解释，在此将不再重复。绘制一个完整的相图等温截面，往往需要很多条结线数据，因此通常需要进行多条EPMA线扫描。图3(c)所示为测得的Cr-Ni-Ru三元系相图在1000 ℃的等温截面，图3(c)中虚线即为结线，每条虚线连接的两个数据点为两相平衡的成分。

3  相图的热力学优化

随着计算机技术的高速发展，相图热力学计算已成为相图研究的重要方向，并使相图研究有了长足的发展。目前获得相图最为活跃的方法是包含相图热力学以及相变动力学在内的CALPHAD方法，其核心是根据实验数据(主要是二元和三元相图，再加上形成焓、混合焓、比热、活度等热力学数据)评估获得多元体系中各相在整个成分范围与从室温298.15 K到6000 K温度范围内的吉布斯自由能随成分、温度变化的关系式，然后通过整合、集成子二元体系、子三元体系的热力学模型和参数来外推获得多组元热力学数据库，以预测多组元体系的热力学性质和相平衡关系。因此，实验结果特别是测定的三元相图是拟合可靠的热力学参数的重要输入，也是建立可靠的多组元热力学数据库的基本保障，而CALPHAD及其热力学数据库是实现多组元合金相关相图计算和合金设计的关键。

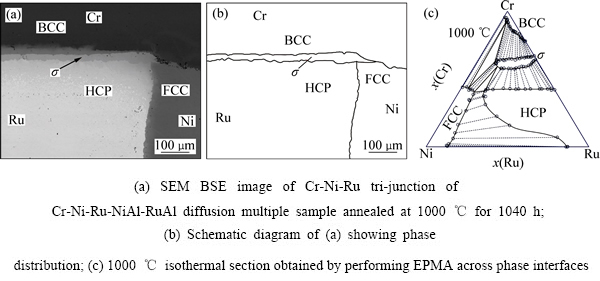
图3  Cr-Ni-Ru三元系相图的测定

Fig. 3  Phase diagram determination of Cr-Ni-Ru ternary system

3.1  实验数据的收集与评估

相图计算的可靠与否很大程度上取决于实验数据的来源是否准确，所以在进行热力学优化之前，需要对文献中报道的所有实验数据，包括晶体结构数据、实测相图数据、热力学数据以及亚稳相实验数据等，进行全面的收集、分析和评估。

Cr-Ni-Ru三元体系由Cr-Ni、Ni-Ru和Cr-Ru 3个二元系组成。其中Cr-Ni^[50-51]和Ni-Ru^[46]二元系已有较为完善的实验数据，并且已经被很好地优化与评估。但Cr-Ru二元系的实验数据却存在着两点争议，一是σ相的成分范围，二是HCP(Ru)/HCP(Ru)+σ相边界的位置。同时Cr-Ni-Ru三元系中可用的实验数据也非常少。通过扩散多元节的方法，ZHU等^[49]获得了大量可靠的Cr-Ru二元系与Cr-Ni-Ru三元系的相图数据。这些相图数据及文献中的其他可靠数据可用于对Cr-Ru二元系及Cr-Ni-Ru三元系的热力学优化。

3.2  热力学模型的选择

热力学优化时，需要根据评估后的相图、热力学和晶体结构等信息，选择恰当的热力学模型来描述各相的吉布斯自由能。在Cr-Ni-Ru三元体系中存在着7个稳定相，它们分别是液相、FCC相、BCC相、HCP相、σ相(典型的TCP相)、Cr₃Ru相与Ni₂Cr相。其中液相、FCC相、BCC相、HCP相是完全无序的替代式固溶体，可采用规则溶体模型(Regular solution model)进行描述；Cr₃Ru相与Ni₂Cr相的成分范围非常窄，可近似地将它们当作线性化合物(Linear compound)处理，其吉布斯自由能可用Neumann-Kopp法则表示；中间化合物σ相的成分范围为(32±2)%~(36±2)% Ru(摩尔分数)，因此不能再将其当作线性化合物，在描述其吉布斯自由能表达式时，需要采用化合物能量模型(Compound energy formalism, CEF)^[52]。在σ相中，一个晶胞中含有30个原子，分别占据着5种独立的点阵类型，相应的点阵类型中分别含有2、4、8、8和8个原子。为了减少σ相吉布斯自由能表达式中的参数，ANDERSON等^[53-54]和ANSARA等^[55]将其简化为3个亚点阵。后来，为了便于多组元镍基高温合金热力学数据库的建立与完善，JOUBERT^[56]提出了一个更加简化且完整对称的两个亚点阵模型(A,B)₂₀(A,B)₁₀来描述σ相。ZHU等^[49]采用(Cr,Ru)₂₀(Cr,Ru)₁₀两个点阵模型对Cr-Ru二元系中的σ相及(Cr,Ni,Ru)₂₀(Cr,Ni,Ru)₁₀两个点阵模型对Cr-Ni-Ru三元系中的σ相进行了热力学优化。

3.3  Cr-Ni-Ru三元系热力学数据库的快速建立

ZHU等^[49]采用Thermo-Calc软件^[57-58]中的PARROT模块重新对Cr-Ru二元系和Cr-Ni-Ru三元系进行了热力学优化计算，快速建立了Cr-Ni-Ru三元系的热力学数据库。图4(a)所示为利用所建立的热力学数据库，计算的Cr-Ru二元系相图。图4(b)所示为计算的Cr-Ni-Ru三元系相图在1000 ℃的等温截面，并与ZHU等^[49]采用扩散多元节方法测定的两相结线进行了比较，可以看出热力学优化计算结果与实验数据的一致性非常好。通过热力学优化，可获得描述Cr-Ni-Ru体系中各相吉布斯自由能表达式的所有参数，然后可以将这些参数集成到当前的镍基高温合金热力学数据库中，进而指导含Ru镍基高温合金的成分与工艺设计。

图4  Cr-Ni-Ru三元系热力学数据库的建立

Fig. 4  Establishment of thermodynamic database of Cr-Ni-Ru ternary system

4  结论与展望

针对镍基高温合金中TCP相相关的Cr-Ni-Ru 三元体系，采用扩散多元节方法，高通量地测定了Cr-Ni-Ru三元系相图等温截面。并且在此基础上，优化了Cr-Ru二元系和Cr-Ni-Ru三元系热力学数据。计算的Cr-Ru二元系和Cr-Ni-Ru三元系相平衡结果与实验和文献数据具有很好的一致性。在 CALPHAD 框架内，可将其集成到当前镍基高温合金热力学数据库中，提高对含 Ru 高温合金体系中的相平衡关系及 σ 相形成范围的预测能力。

目前镍基高温合金的研究效率低下，主要有以下两个原因：一是高温合金体系非常复杂，通常含有10种以上的合金元素，对于各元素之间的交互作用及在复杂高温力场中元素与微观组织演化对合金性能的作用机理尚没有系统地认识；二是在很大程度上仍然延续传统的试错法的材料研究方法，这大大增加了合金的研发费用与研发周期，而且往往只能找到某些性能所对应的特殊解。快速建立与定量预测材料成分-相-组织-性能关系的高通量方法是促进未来镍基高温合金研究发展的重点，也是实现镍基高温合金的设计从盲目的“炒菜”转变为根据实际需要“定制”具有某些性能的关键所在。

以吉布斯自由能为主线的 CALPHAD方法在热力学计算和热力学数据库的建立方面取得了巨大成就，其框架已非常成熟。用CALPHAD方法预测合金成分，再与材料性能数据库和模型相结合来进行合金设计是非常有效的途径。当前CALPHAD发展的还主要集中在建立可靠的数据库和扩展数据库中所包括的元素，为多组元复杂合金体系的成分设计和工艺优化提供更好的预测。作为高通量实验方法的一种，扩散多元节方法极大地加快了相图的系统而且高效的测定，为多组元镍基高温合金热力学数据库的建立与完善积累大量可靠的二元和三元实验相图信息。

然而，采用CALPHAD方法在热力学数据以外的物理性质如体积、热膨胀系数、弹性模量等模型的建立却有待进一步完善。在CALPHAD方法框架内建立定量描述这些物理性质的模型，除了需要在理论上不断突破与创新，同时也需要大量可靠的实验数据来检验理论模型的准确性。在扩散多元节中，高温长时间扩散可形成具有宽广成分梯度的固溶体和金属间化合物相，将其与微区性能测试方法相结合，能数量级地提高材料微区性能测试效率，快速建立和完善材料的成分-相-组织-性能数据库，为新材料的研究和快速开发提供指导。因此，仍需要加强实验工具平台的建设与改进，开发新的微区材料性能测试方法。

REFERENCES

[1] REED R C. The superalloys: Fundamentals and applications[M]. New York: Cambridge University Press, 2006.

[2] 郭建亭. 几种微量元素在高温合金中的作用与机理[J]. 中国有色金属学报, 2011, 21(3): 465-475.

GUO Jian-ting. Effects of several minor elements on superalloys and their mechanism[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(3): 465-475.

[3] 郭建亭. 高温合金材料学(上) 应用基础理论[M]. 北京: 科学出版社, 2008.

GUOJian ting. Materials science and engineering for superalloys (Volume one): Application of basic theory[M]. Beijing: Science Press, 2008.

[4] POLLOCK T M, TIN S. Nickel-based superalloys for advanced turbine engines: Chemistry, microstructure and properties[J]. Journal of Propulsion and Power, 2006, 22(2): 361-374.

[5] BLAVETTE D, CARON P, KHAN T. An atom probe investigation of the role of rhenium additions in improving creep resistance of Ni-base superalloys[J]. Scripta Metallurgica, 1986, 20(10): 1395-1400.

[6] SHI Z X, LI J R, LIU S Z. Effects of Ru on the microstructure and phase stability of a single crystal superalloy[J]. International Journal of Minerals, Metallurgy, and Materials, 2012, 19(11): 1004-1009.

[7] CHATTERJEE D, HAZARI N, DAS N. Influence of Ru addition on microstructure, creep and rupture properties of nickel based DS superalloy[J]. Procedia Engineering, 2013, 55: 51-57.

[8] RAE C, REED R C. The precipitation of topologically close-packed phases in rhenium-containing superalloys[J]. Acta Materialia, 2001, 49(19): 4113-4125.

[9] YANG J, ZHENG Q, SUN X, GUAN H R, HU Z Q. Topologically close-packed phase precipitation in a nickel-base superalloy during thermal exposure[J]. Materials Science and Engineering A, 2007, 465(1): 100-108.

[10] 王绍青, 叶恒强. 晶体材料基因组问题第一原理计算研究[J]. 科学通报, 2013, 58(35): 3623-3632.

WANG Shao-qing, YE Heng-qiang. First-principles calculation of crystalline materials genome[J]. Science Bulletin, 2013, 58(35): 3623-3632.

[11] REED R C, TAO T, WARNKEN N. Alloys-by-design: application to nickel-based single crystal superalloys[J]. Acta Materialia, 2009, 57(19): 5898-5913.

[12] FETZER R S. Phase diagrams: The beginning of wisdom[J]. Journal of Phase Equilibria and Diffusion, 2014, 35(6): 735-760.

[13] SAUNDERS N, MIODOWNIK A P. Calphad (Calculation of Phase Diagrams): A comprehensive guide[M]. New York: Elsevier, 1998.

[14] ZHAO J C, FAHRMANN M, POLLOCK T M. Materials design approaches and experiences[M]. Warrendale: TMS, 2001.

[15] Committee on Benchmarking the Technology and Application of Lightweighting NRC. Application of lightweighting technology to military vehicles, vessels, and aircraft[M]. Washington DC: The National Academies Press, 2012: 118-119.

[16] JIANG L, ZHAO J C, FENG G. Nickel-containing alloys, method of manufacture thereof and articles derived therefrom. World Patent Application WO2005056852[P]. 2004-09-29.

[17] ZHAO J C, HENRY M F. CALPHAD—Is it ready for superalloy design?[J]. Advanced Engineering Materials, 2002, 4(7): 501-508.

[18] ZHAO J C. Methods for phase diagram determination[M]. New York: Elsevier, 2007.

[19] SHAO G, TSAKIROPOULOS P. Solidification structures of Ti-Al-Cr alloys[J]. Intermetallics, 1999, 7(5): 579-587.

[20] CARTER G C, KAHAN D, BENNETT L. Applications of phase diagrams in metallurgy and ceramics[M]. Washington DC: US Government Printing Office, 1978.

[21] 金展鹏. 三元扩散偶及基在相图研究中的应用[J]. 中南矿冶学院学报, 1984, 15(1): 27-35.

JIN Zhan-peng. The application of ternary diffusion couple technique to study phase diagram[J]. Journal of Central-South Institute of Mining and Metallurgy, 1984, 15(1): 27-35.

[22] Jin Z P. A study of the range of stability of sigma phase in some ternary systems[J]. Scandinavian Journal of Metallurgy, 1981, 10(6): 279-287.

[23] 王日初, 王 冲, 金展鹏. 三元扩散偶中的相区分布与四相平衡的关系[J]. 中国有色金属学报, 2002, 12(4): 643-647.

WANG Ri-chu, WANG Chong, JIN Zhan-peng. Relation between phase field distribution in diffusion triple and quaternary phase equilibria[J]. The ChineseJournal of NonferrousMetals, 2002, 12(4): 643-647.

[24] van LOO F J J. Multiphase diffusion in binary and ternary solid-state systems[J]. Progress in Solid State Chemistry, 1990, 20(1): 47-99.

[25] KODENTSOV A, BASTIN G, van LOO F J J. The diffusion couple technique in phase diagram determination[J]. Journal of Alloys and Compounds, 2001, 320(2): 207-217.

[26] 郝士明. 局域平衡原理与相图的扩散偶法测定[J]. 材料与冶金学报, 2004, 2(3): 203-209.

HAO Shi-ming. Local phase equilibrium principle and diffusion couple method for determination of phase diagrams[J]. Journal of Materials and Metallurgy, 2004, 2(3): 203-209.

[27] 赵继成. 材料基因组计划简介[J]. 自然杂志, 2014, 2(3): 89-104.

ZHAO Ji-cheng. A perspective on the materials genome initiative[J]. Chinese Journal of Nature, 2014, 2(3): 89-104.

[28] ZHAO J C. A combinatorial approach for structural materials[J]. Advanced Engineering Materials, 2001, 3(3): 143-147.

[29] ZHAO J C. The diffusion-multiple approach to designing alloys[J]. Annual Review of Materials Research, 2005, 35: 51-73.

[30] ZHAO J C. Combinatorial approaches as effective tools in the study of phase diagrams and composition-structure-property relationships[J]. Progress in Materials Science, 2006, 51(5): 557-631.

[31] CAO S, ZHAO J C. Application of dual-anneal diffusion multiples to the effective study of phase diagrams and phase transformations in the Fe-Cr-Ni system[J]. Acta Materialia, 2015, 88: 196-206.

[32] ZHAO J C. Reliability of the diffusion-multiple approach for phase diagram mapping[J]. Journal of Materials Science, 2004, 39(12): 3913-3925.

[33] 赵继成. 材料基因组计划中的高通量实验方法[J]. 科学通报, 2013, 58(35): 3647-3655.

ZHAO Ji-cheng. High-throughput experimental tools for the materials genome initiative[J]. Science Bulletin, 2013, 58(35): 3647-3655.

[34] SATO A, HARADA H, YOKOKAWA T, MURAKUMO T, KOIZUMI Y, KOBAYASHI T, IMAI H. The effects of ruthenium on the phase stability of fourth generation Ni-base single crystal superalloys[J]. Scripta Materialia, 2006, 54(9): 1679-1684.

[35] CHEN J Y, FENG Q, SUN Z. Topologically close-packed phase promotion in a Ru-containing single crystal superalloy[J]. Scripta Materialia, 2010, 63(8): 795-798.

[36] CHEN J Y, FENG Q, CAO L M, SUN Z Q. Influence of Ru addition on microstructure and stress-rupture property of Ni-based single crystal superalloys[J]. Progress in Natural Science: Materials International, 2010, 20: 61-69.

[37] SUN F, ZHANG J X. Influence of Ru on the microstructure of Ni-base single crystal superalloys[J]. Advanced Materials Research, 2011, 306: 562-571.

[38] YEH A, TIN S. Effects of Ru on the high-temperature phase stability of Ni-base single-crystal superalloys[J]. Metallurgical and Materials Transactions A, 2006, 37(9): 2621-2631.

[39] CHAKRAVORTY S, WEST D R F. Phase equilibria between NiAl and RuAl in the Ni-Al-Ru system[J]. Scripta Metallurgica, 1985, 19(11): 1355-1360.

[40] CHAKRAVORTY S, WEST D R F. The constitution of the Ni-Al-Ru system[J]. Journal of Materials Science, 1986, 21(8): 2721-2730.

[41] HORNER I J, CORNISH L A, WITCOMB M J. A study of the Al-Ni-Ru ternary system below 50 at.% aluminium[J]. Journal of Alloys and Compounds, 1997, 256(1): 213-220.

[42] HORNER I J, CORNISH L A, WITCOMB M J. Constitution of the Al-Ni-Ru ternary system above 50 at.% aluminium[J]. Journal of Alloys and Compounds, 1997, 256(1): 221-227.

[43] HORNER I J, HALL N, CORNISH L A, WITCOMB M J, CORTIE M B, BONIFACE T D. An investigation of the B2 phase between AlRu and AlNi in the Al-Ni-Ru ternary system[J]. Journal of Alloys and Compounds, 1998, 264(1): 173-179.

[44] TRYON B, POLLOCK T. Experimental assessment of the Ru-Al-Ni ternary phase diagram at 1000 and 1100 ℃[J]. Materials Science and Engineering: A, 2006, 430(1): 266-276.

[45] . Thermodynamic reassessment of the Ni-Ru system and assessment of the Al-Ni-Ru system at 1273-1523K using ab initio calculations[J]. Acta Materialia, 2008, 56(15): 4062-4069.

[46] ZHU J, ZHANG C, CAO W, YANG Y, ZHANG F, CHEN S, MORGAN D, CHANG Y A. Experimental investigation and thermodynamic modeling of the Ni-Al-Ru ternary system[J]. Acta Materialia, 2009, 57(1): 202-212.

[47] CHAKRAVORTY S, WEST D R F. Constitution of Ni-Cr-Ru system[J]. Materials Science and Technology, 1985, 1(3): 249-254.

[48] ZHU J. Thermodynamic description of multicomponent Ni-base superalloys containing Al, Cr, Ru and Pt: A computational thermodynamic approach coupled with experiments[D]. Madison: University of Wisconsin-Madison, 2008.

[49] ZHU L L, QI H Y, JIANG L, JIN Z P, ZHAO J C. Experimental determination of the Ni-Cr-Ru phase diagram and thermodynamic reassessments of the Cr-Ru and Ni-Cr-Ru systems[J]. Intermetallics, 2015, 64: 86-95.

[50] LEE B J. On the stability of Cr carbides[J]. Calphad, 1992, 16(2): 121-149.

[51] CHAN K S, PAN Y M, LEE Y D. Computation of Ni-Cr phase diagram via a combined first-principles quantum mechanical and CALPHAD approach[J]. Metallurgical and Materials Transactions A, 2006, 37(7): 2039-2050.

[52] HILLERT M. The compound energy formalism[J]. Journal of Alloys and Compounds, 2001, 320(2): 161-176.

[53] ANDERSSON J O, GUILLERMET A F, HILLERT M, JANSSON B, SUNDMAN B. A compound-energy model of ordering in a phase with sites of different coordination numbers[J]. Acta Metallurgica, 1986, 34(3): 437-445.

[54] ANDERSSON J O, SUNDMAN B. Thermodynamic properties of the Cr-Fe system[J]. Calphad, 1987, 11(1): 83-92.

[55] ANSARA I, CHART T, GUILLERMET A F, HAYES F H, KATTNER U R, PETTIFOR D G, SAUNDERS N, ZENG K. Thermodynamic modelling of solutions and alloys[J]. Calphad, 1997, 21(2): 171-218.

[56] JOUBERT J M. Crystal chemistry and Calphad modeling of the σ phase[J]. Progress in Materials Science, 2008, 53(3): 528-583.

[57] SUNDMAN B, JANSSON B, ANDERSSON J O. The thermo-calc databank system[J]. Calphad, 1985, 9(2): 153-190.

[58] ANDERSSON J O, HELANDER T, , SHI P F, SUNDMAN B. Thermo-Calc & DICTRA, computational tools for materials science[J]. Calphad, 2002, 26(2): 273-312.

(编辑  龙怀中)

基金项目：国家高技术研究发展计划资助项目(2012AA03A514)；有色金属先进结构材料与制造协同创新中心研究生拔尖创新人才培养；中南大学中央高校基本科研业务费专项基金资助项目(2014zzts171)；国家自然科学基金资助项目(51401242, 61271356, 51205031, 51301209)

收稿日期：2015-02-25；修订日期：2015-08-20

通信作者：江  亮，博士，教授；电话：0731-88877812；E-mail：liang.jiang@csu.edu.cn